星载原子干涉重力梯度仪测量方法与噪声分析

祝 竺，张国万，赵艳彬，廖 鹤，魏小刚

（1. 上海卫星工程研究所，上海 201109；2. 北京航天控制仪器研究所，北京 100854；3. 中国航天科技集团量子工程研究中心，北京 100854）

星载原子干涉重力梯度仪测量方法与噪声分析

祝 竺1，张国万2,3，赵艳彬1，廖 鹤1，魏小刚2,3

（1. 上海卫星工程研究所，上海 201109；2. 北京航天控制仪器研究所，北京 100854；3. 中国航天科技集团量子工程研究中心，北京 100854）

原子干涉重力梯度仪在星载环境下可获得较长的干涉时间，有效规避了原子触碰容器壁的风险，因此可实现高精度的测量，同时利于星载仪器的小型化。目前原子干涉重力梯度仪地面测量技术成熟，尚未得到空间应用。根据星载失重的特殊条件，提出一种适用于空间微重力环境的原子干涉重力梯度测量方法，并对其测量精度进行了分析。结果表明，在卫星重力测量关注的0.1 Hz以下的测量频带内，星载原子干涉重力梯度仪的潜在测量精度可达到 1 mE/Hz1/2。该测量方法为未来原子干涉重力梯度仪的星载应用提供重要的技术基础。

原子干涉；重力梯度仪；星载；噪声

星载重力梯度仪是卫星重力测量的核心载荷之一，主要用于高精度获取全球重力场模型，在大地测量、地球科学、惯性导航等领域发挥着重要作用[1-2]。目前国内外研制的星载重力梯度仪主要采用差分加速度的测量原理，由相隔一定基线长度的一对或多对重力仪构成差分测量，来获取轨道高度处重力加速度g随空间的变化（重力位V的二阶导数），即重力梯度张量：

重力梯度仪有静电式、超导式、原子干涉式、旋转加速度计式等多种类型[3-5]。对于星载应用而言，静电式重力梯度仪结构简单，技术成熟度高，已成功应用于GOCE重力梯度卫星，设计精度7 mE/Hz1/2，在轨实测分辨率约为 10～20 mE/Hz1/2，但其量程小，极易饱和，且受电路噪声、加工工艺和低频机械热噪声的限制，测量精度提升空间有限[3]；超导式重力梯度仪噪声低、机械稳定性好，Maryland 大学研制的单轴超导重力梯度仪实验样机的灵敏度可达到1 mE/Hz1/2，但其结构复杂，且需配备低温保持系统，目前尚未进入星载工程化应用阶段；原子干涉式重力梯度仪通过相距一段距离的原子团与激光进行相互作用完成干涉，通过测量干涉条纹相移来获取差分加速度信息，进而得到该方向上的重力梯度值，具有稳定性高、量程大、测量频带宽、低频白噪声谱平稳、星载潜在测量精度高等诸多优点[4,6]，成为近年来飞速发展的重力测量仪器之一。

1998年斯坦福大学研制出了地面首台原子干涉重力梯度仪，该类型的重力梯度仪的测量分辨率与干涉时间间隔T的平方成反比，由于地面受到1g重力加速度和仪器尺寸的限制，原子需在很短的时间内下落完毕并完成干涉，因此T只能维持在ms量级，故该台原子干涉重力梯度仪在1.4 m的基线长度下，测量分辨率仅为30 E/Hz1/2。空间微重力环境下，原子失重，有效规避了原子快速下落触碰容器壁的风险，因此T很容易增大到数十秒量级，一方面大幅度提升测量精度，另一方面可缩短作用区真空腔长度，利于星载装置的小型化，具有非常高的星载应用前景。因此近年来国际上开始关注并研究原子干涉重力梯度仪的星载应用。JPL首先提出了星载原子干涉重力梯度仪概念[7]，随后NASA与ESA开展了星载便携式原子干涉重力梯度仪样机的研制及落塔、机载实验，并指出原子干涉式重力梯度仪的测量分辨率预计比成功搭载在GOCE卫星上的静电式重力梯度仪至少高1～2个数量级[8]。

近年来，NASA与ESA均瞄准原子干涉仪的星载应用优势，推出了一系列原子干涉仪的搭载和在轨验证计划[8]，并指出目前原子干涉仪的发展为两个方向：一是提高仪器精度，二是推动星载原子干涉仪的小型化。

在该背景下，本文基于原子干涉重力梯度仪的测量原理，提出并阐述了一种适用于空间微重力环境的原子干涉重力梯度仪的测量方法，然后具体分析了原子干涉重力梯度仪的星载噪声源以及潜在测量分辨率，为原子干涉重力梯度仪的星载应用提供一定的理论参考和技术支撑。

1 星载原子干涉重力梯度仪测量方法

1.1 地面测量方法

原子干涉重力测量的基本原理是利用自由落体运动的超冷原子作为检验质量来感应重力的作用，通过相位相干的Raman激光对冷原子操控实现原子干涉，使原子所处叠加态的相位与运动路径中受到的重力加速度相关，检测原子的内态，通过干涉条纹拟合得到的相位便可获取重力加速度信息。

原子干涉重力梯度仪是原子干涉重力仪的差分应用形式。通过测定干涉相位差 Δφ获得同一方向上的差分加速度Δa，可表示为

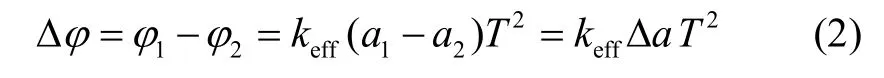
其中，keff是Raman激光脉冲的有效波矢，T是激光脉冲间隔。

地面上通过磁光阱（MOT）将原子冷却囚禁，通过竖直上抛不同高度的冷原子，在地表1g重力加速度的作用下原子下落并与激光作用，发生干涉，继而感测出不同高度处的重力加速度，得到竖直方向上的重力梯度值Vzz，如图1所示，此时式(1)中Δa=VzzL（L为原子团之间的高度差）。

图1 原子干涉重力梯度仪地面测量方法Fig.1 On-ground measurement method of atominterferometry-based gravity gradiometer

1.2 空间测量方法

星载微重力环境下，原子失重接近自由飘浮状态，有效避免了原子快速下落的风险，因此可获得较长的干涉时间间隔T，大大提高测量精度。此时上抛下落式的测量方法不再适用，为提升星载原子干涉重力梯度仪测量精度，同时考虑星载小型化以及卫星角速度引入离心力的影响[9]，我们提出了释放飘浮式的星载测量方法：1）沿卫星质心对称放置MOT，其中MOT1与4置于X轴（飞行方向）基线上，MOT2与5置于Y轴（垂直轨道平面方向）基线上，MOT3与 6置于Z轴（地心径向）基线上；2）用MOT将原子冷却囚禁；3）关闭线圈电流，使MOT失效，让原子处于自由飘浮状态；4）在每个方向上分别用Raman激光与飘浮的原子团相互作用，完成原子干涉，通过测量相位差获取差分加速度信息；5）采用星敏感器、陀螺仪等高精度星上测姿仪器获取卫星角速度，并在差分加速度测量中扣除，以得到重力梯度值。整套测量方案如图2所示。

图2 原子干涉重力梯度仪星载测量方法Fig.2 Space-borne measurement method of atom-interferometry-based gravity gradiometer

此时式(2)中Δa可表示为

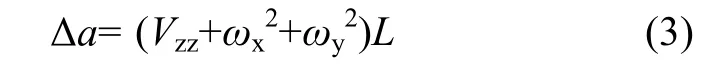
其中，Vzz是沿地心径向重力梯度值，ωx与ωy分别是卫星沿X轴与Y轴的角速度。

从上述公式可以看出：

1）微重力环境原子飘浮状态下，测量的差分加速度非常小，在500 km以下的近地轨道，不超过10–6m/s2量级，此时不需要采用地面上抛原子团的方法进行测量，直接用Raman激光与两团飘浮的原子进行作用，既可获得较大的干涉时间间隔T，提高测量精度，又有利于设备的小型化；

2）每个方向用同样的Raman激光与两团原子相互作用，通过差分测量，可以获得很好的共模抑制效果，对卫星平台振动、Raman光相位噪声至少有80～155 dB的抑制作用[7]，这对于提高测量灵敏度十分有利；

3）地面受1g重力加速度影响，采用上抛下落的方式只能测量竖直方向的重力梯度值Vzz，而空间环境下原子处于悬浮状态，因此不受测量方向的限制，可同时采用多束不同方向的 Raman激光与原子相互作用，测量X、Y、Z三轴的相对加速度，因此可实现Vxx、Vyy、Vzz多个梯度分量的测量。

由上述星载测量方法可知，在空间微重力环境下，原子干涉重力梯度仪通过测量相位差获取重力梯度值，由式(2)(3)可知，相位差Δφ里既包含了轨道高度处的重力梯度值，又携带有卫星角速度信息，其中卫星角速度可通过星敏感器、陀螺仪等星上高精度测姿系统获取，并在重力梯度提取过程中扣除。因此，星载原子干涉重力梯度仪的测量对角梯度分量的表达式可写为

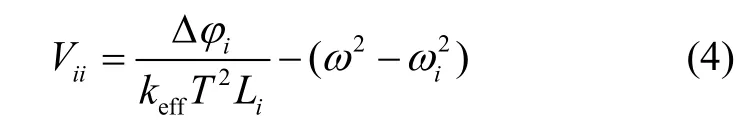
其中，Vii(i=x,y,z)表示待测的重力梯度分量，Δφi(i=x,y,z)表示i方向上测量的相位差，Li(i=x,y,z)为i方向上的基线长度，ω2=ωx2+ωy2+ωz2表示卫星角速度，ωi为卫星i轴的角速度。

2 原子干涉重力梯度仪星载测量分辨率研究

由星载工作原理可知，相比于地面而言，原子干涉重力梯度仪在空间微重力环境下具有很高的测量分辨率。然而星载环境下，原子干涉重力梯度仪高精度的测量不仅取决于原子干涉重力梯度仪自身仪器噪声，同时需要卫星角速度的高精度提取以及稳定的空间环境作为保障。因此星载环境下，原子干涉重力梯度仪测量对角梯度分量的噪声δVii可表示为

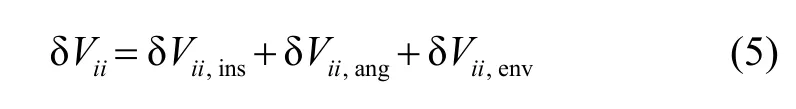
其中，δVii,ins为梯度仪的仪器噪声，δVii,ang为卫星角速度提取噪声，δVii,env为空间环境噪声。为满足卫星重力测量的科学需求，这里主要关注0.1 Hz以下的测量频带内的噪声[1]。

2.1 仪器噪声

在星载重力梯度测量中，梯度仪仪器自身噪声是最主要的误差源。根据式(4)，重力梯度仪测量噪声取决于相位噪声δ(Δφ)、激光有效波矢的稳定度δkeff、激光脉冲间隔T的控制精度δT、测量基线的稳定度δLi，在频域内可表示为：

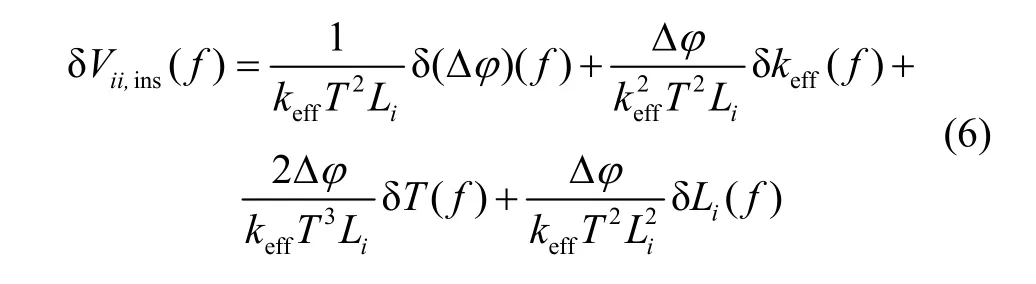
1）相位噪声

相位分辨率δ(Δφ)根本上受限于量子投影噪声，量子投影噪声直接反比于原子数目N的平方根，即δ(Δφ)≈1/N1/2。在原子干涉测量中，采集的原子数可高达 1010个[7]，按选态时损失一个量级计算（即N=109），则干涉仪相移分辨率δ(Δφ)可达 0.03 mrad。以87Rb原子为例，拉曼光有效波矢keff=2π/390 nm，在微重力环境下原子失重，接近自由飘浮状态，原子相对于仪器框架的平均速率为0，时间T仅受限于热运动的扩散速率，因此在作用区真空腔内，T可达到秒量级甚至更高，这里为实现卫星重力测量的空间分辨率需求，设干涉时间T=3.5 s[10]。同时为保证星载设备小型化，参考已在轨应用的静电重力梯度仪，设测量基线L=0.5 m[3]。在条纹对比度100%的理想情况下，根据式(6)，相位噪声贡献的梯度仪的测量分辨率可达ΔVii=0.32 mE，在f＜1/(2T)的频带内，测量噪声可达

2）激光有效波矢的稳定度

激光有效波矢keff的稳定度主要取决于Raman光的频率稳定度，目前有效波矢的相对稳定度δkeff/keff=10–9/Hz1/2较易实现，因此这部分误差贡献的梯度噪声小于0.003 mE/Hz1/2；

3）激光脉冲间隔的控制精度

激光脉冲间隔T的控制精度可由高精度星载原子钟保证，目前我国“天宫二号“上搭载的全球首台冷原子钟的精度已高达三千万年差1 s，即δT=1×10–15，因此其贡献的梯度测量分辨率为ΔVii=1.6×10–9mE，测量频带内的噪声为可忽略不计。

4）测量基线的稳定度

对于高稳定度的测量基线Li(i=x,y,z)而言，鉴于重力梯度卫星GOCE的技术经验，目前在Li=0.5 m的基线长度下，基于超稳碳碳结构的基座稳定度可达到 δLi=1 nm/Hz1/2，其贡献的梯度测量噪声优于0.005 mE/Hz1/2。

综合上述噪声分析，星载原子干涉重力梯度仪的的自身仪器测量潜在分辨率可以达到0.85 mE/Hz1/2，如表1所示。

表1 星载原子干涉重力梯度仪仪器噪声Tab.1 Instrument noise of space-borne atominterferometry-based gravity gradiometer

2.2 卫星角速度提取噪声

卫星角速度的提取是星载重力梯度测量中的关键步骤之一。根据式(4)，卫星角速度 (i=x,y,z)的测量噪声δω贡献的梯度测量噪声可表示为

其中，下标i、j与k为空间三维正交自由度（i,j与k=x,y,z），且按顺序满足右手法则。

卫星角速度可由两种途径获取：一种是通过给原子一个初始速度，形成一种差分对抛式的星载原子干涉重力梯度仪测量方法，研究结果表明，该方法可将卫星角速度测量至 2.5×10–11(rad·s–1)/Hz1/2的水平[4]，则根据式(7)，该方法贡献的梯度测量噪声约为 0.06 mE/Hz1/2；而本文设计的重力梯度仪是基于自由飘浮式，可由另一种方法即高精度的卫星测姿系统来实现。一般对于频率低于10 Hz的角运动，航天器主要采用高精度陀螺仪或光学敏感器测量，比如激光陀螺或原子陀螺仪[11-12]，其中激光陀螺仪灵敏度可以达到δωi=2×10–10(rad·s–1)/Hz1/2[11]。值得注意的是，由于重力卫星对地三轴稳定，卫星Y轴存在一个较大的公转角频率ωy≈1.2×10–3rad/s2，而X与Z轴的角速度较小，约为ωx≈ωz=6.5×10–6rad/s，则根据式(7)，可以计算出卫星角速度测量噪声贡献的Vxx与Vzz梯度分量测量噪声为约0.5 mE/Hz1/2，Vyy梯度分量测量噪声为约0.004 mE/Hz1/2，如表2所示。

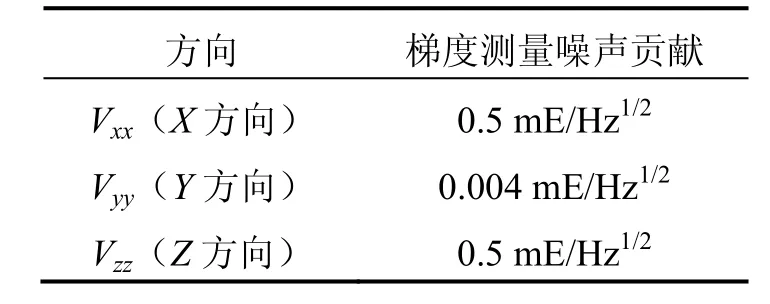
表2 卫星角速度测量贡献的梯度测量噪声Tab.2 Gradient noise caused by satellite angular velocity measurement

2.3 空间环境噪声

星载环境下，电磁、振动等外场空间环境波动变化对原子干涉重力梯度仪测量精度的影响不可忽略[13]，主要体现在平台振动、轨道高低温交变、背景磁场、电场等方面。其中卫星平台的振动影响在差分测量的机理下通过共模抑制和主动隔振技术衰减80～140 dB[7,14]。温度主要影响腔体的真空度、激光功率以及偏振频率等，该部分影响可通过星上温控系统得到很好的抑制，而磁场与电场分别通过二阶 Zeeman效应和 DC/ACStark效应影响重力梯度测量分辨率，其中电场影响可通过均匀布局、适当调节Raman光的光强比等手段得到抑制，而背景磁场噪声在星载环境下较为复杂，是星载外场环境干扰中最主要的误差源[15]。磁场波动通过相移贡献梯度测量噪声，可表示为

对某一处干涉区而言，完成一次干涉测量需要2T的时间，而卫星飞过的 2T时间内，背景磁场主要体现在以下三方面：

1）干涉区线圈电流磁场：主要是由产生偏置磁场的线圈电流波动引起。为降低磁场影响，采用双层合金进行磁屏蔽。为了星载设备的轻量化和小型化设计，可考虑采用磁补偿和磁场锁定的方法来保证干涉区磁场的稳定性和均匀性。屏蔽后的剩余磁场B可达25 μG[15]，一般两个干涉区的磁场差ΔB=B/100，磁场波动δ(ΔB)= ΔB/200。

2）空间地磁场：空间磁场的影响主要来自于轨道高度处的地球磁场梯度。空间微重力环境下，在2T=7 s的时间内[10]，卫星飞过了d=vT=55 km的距离（其中低轨卫星速度v=7.8 km/s），由于近地空间存在∂B/∂r=10–8G/m大小的地磁场梯度以及8×10–8G/m的磁场波动[16]，干涉区磁场将产生BB/r dΔ =∂ ∂·=0.5 mG的变化以及4 mG/Hz1/2的磁场波动。

3）卫星平台磁场：星上各单机的磁性耦合、模式切换、星内布局、电流波动等带来磁场变化ΔB。为降低磁场影响，一方面，星上不采用磁力矩器等大磁性单机，另一方面，通过改善布局、单机降磁设计等手段控制星上剩磁。目前情况来看，卫星整星内部磁场不大于地磁场。这里采取最大化考虑，即整星内部磁场等于地磁场。

经磁屏蔽设计后，空间地磁场和卫星平台磁场可以下降约100倍。三类磁场贡献的梯度测量噪声合计约0.14 mE/Hz1/2，如表3所示。

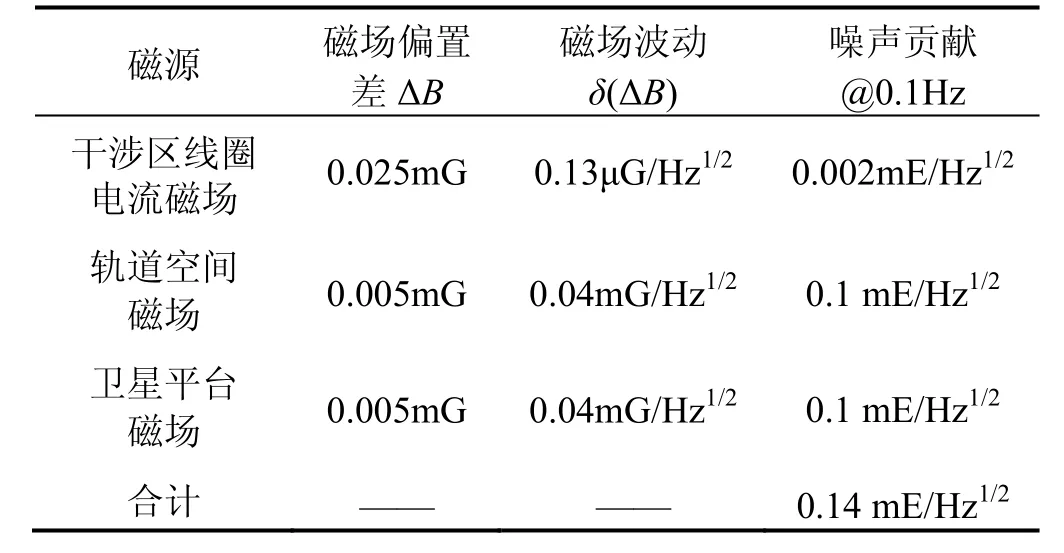
表3 空间中背景磁场贡献的原子干涉重力梯度仪测量噪声Tab. 3 Atom-interferometry-based gravity gradiometer noise caused by background magnetic field in space

2.4 噪声分析小结

由前文噪声分析可知，在卫星重力测量关注的5～100 mHz的测量频带内，星载原子干涉重力梯度仪的测量噪声约 1 mE/Hz1/2，其中，星载原子干涉重力梯度仪仪器噪声为0.85 mE/Hz1/2，卫星角速度提取噪声为0.5 mE/Hz1/2，空间环境噪声为0.14 mE/Hz1/2，如表4所示。

表4 星载原子干涉重力梯度仪测量噪声统计Tab.4 Noise contributions of space-borne atom-interferometry-based gravity gradiometer

星载原子干涉重力梯度仪的噪声谱密度曲线如图 3所示。可以看出，在重力卫星科学测量关注的5～100 mHz频带内，星载原子干涉重力梯度仪的测量灵敏度比现有静电式重力梯度仪的在轨精度 20 mE/Hz1/2高出1个量级。

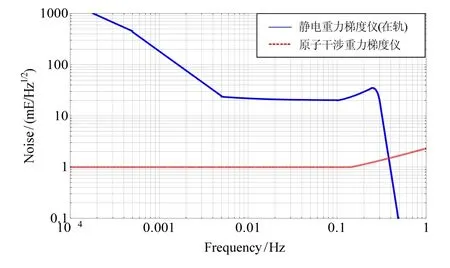
图3 星载原子干涉重力梯度仪噪声谱密度曲线Fig.3 Noise PSD of space-borne atom-interferometry-based gravity gradiometer

3 总 结

原子干涉重力梯度仪具有很高的星载应用价值。一方面，原子干涉重力梯度仪在空间中具有很高的测量灵敏度，本文设计了一种基于释放飘浮式测量原理的星载原子干涉重力梯度仪，在0.1 Hz以下的测量频带，其测量精度可达1 mE/Hz1/2，比地面测量精度提高3个量级，比目前已在轨应用的静电式星载重力梯度仪精度高出1个量级。另一方面，空间环境下原子失重，有效规避了原子短时间内触碰容器壁的风险，利于该类梯度仪的星载小型化研制。将其作为下一代重力梯度卫星的核心载荷，将进一步提升全球重力场模型的恢复精度。

（References）：

[1]Canciani A, Raquet J. Integration of cold atom interferometery INS with other sensors[C]//Proceedings of the 2012 International Technical Meeting of the Institute of Navigation. Newport Beach, CA, 2012: 151-185.

[2]Tino G F, Rosi G, Sorrentino F, et al. Precision measurement of the gravitational constant with atom interferometry[C]//European Frequency and Time Forum & International Frequency Control Symposium. IEEE, 2013:593-598.

[3]Zhu Z, Zhou Z B, Cai L, et al. Electrostatic gravity gradiometer design for the future mission[J]. Advances in Space Research, 2013, 51: 2269-2276.

[4]Carraz O, Siemes C, Massotti L, et al. A spaceborne gravity gradiometer concept based on cold atom interferometers for measuring Earth’s gravity filed[J]. Microgravity Science and Technology, 2014, 26(3): 139-145.

[5]杨晔, 李达, 高巍. 旋转加速度计式重力梯度仪输出解调与滤波[J]. 中国惯性技术学报, 2016, 24(6): 701-705.Yang Ye, Li Da, Gao Wei. Gradient signal demodulation and filtering for rotating accelerometer gravity gradiometer[J]. Journal of Chinese Inertial Technology, 2016,24(6): 701-705.

[6]Dickerson S M, Hogan J M, Sugarbaker A, et al. Multiaxis inertial sensing with long-time point source atom interferometry[J]. Physical Review Letters, 2013, 111(8): 083001.

[7]Maleki L, Yu N, Kohel J. Quantum gravity gradiometer for sub-surface imaging[C]//Space 2004 Conference and Exhibit. San Diego, California, 2004: AIAA 2004-5906.

[8]Sorrentino F, Bongs K, Bouyer P, et al. The space atom interferometer project: status and prospects[J]. Journal of Physics: Conference Series, 2011, 327: 012050.

[9]Lan S Y, Kuan P C, Estey B, et al. Influence of the coriolis force in atom interferometry[J]. Physical Review Letters, 2012, 108: 090402.

[10]祝竺, 白彦峥, 段小春, 等. 卫星重力梯度测量中星载重力梯度仪潜在测量精度研究[J]. 地球物理学进展,2017, 32(2): 559-565.Zhu Z, Bai Y Z, Duan X C, et al. Potential resolution research of space-borne gravity gradiometer for satellite gravity gradiometry[J]. Progress in Geophysics, 2017,32(2): 559-565.

[11]Stedman G E, Schreiber K U, Bilger H R. On the detectability of the lense-thirring field from rotating laboratory masses using ring laser gyroscope interferometers[J].Classical & Quantum Gravity, 2003, 20(13): 2527-2540.

[12]Fang J C, Qin J. Advances in atomic gyroscopes: a view from inertial navigation applications[J]. Sensors, 2013,12(5): 6331-6346.

[13]Coq Y L, Retter J A, Richard S, et al. Coherent matter wave inertial sensors for precision measurements in space[J]. Advances in Space Research, 2012, 49: 365-372.

[14]Zhou M K, Hu Z K, Duan X C, et al. Performance of a cold-atom gravimeter with an active vibration isolator[J].Physical Review A, 2012, 86(1): 043630.

[15]周腾飞. 磁场稳定性对原子重力仪精密测量的影响[D].杭州: 浙江大学, 2015.Zhou Teng-fei. Effect of the stability of the magnetic field on precision measurement of the atom gravimeter[D].Hangzhou: Zhejiang University, 2015.

[16]刘开磊, 张珩, 李文皓, 等. 近地空间磁场梯度分布特性及磁力效应研究[J]. 航天器环境工程, 2012, 29(5):493-498.Liu Kai-lei, Zhang Heng, Li Wen-hao, et al. The characteristics of geomagnetic field’s gradient distribution and the magnetic force effects in near-earth space[J]. Spacecraft Environment Engineering, 2012, 29(5): 493-498.

Measurement method and noise analysis of spaceborne atom-interferometry-based gravity gradiometer

ZHU Zhu1, ZHANG Guo-Wan2,3, ZHAO Yan-Bin1, LIAO He1, WEI Xiao-Gang2,3
(1. Shanghai Institute of Satellite Engineering, Shanghai 201109, China; 2. Beijing Institute of Aerospace Control Devices, Beijing 100854, China; 3. Quantum Engineering Research Center,China Aerospace Science and Technology Corporation, Beijing 100854, China)

The atom interferometry gradiometer can obtain greatly improved sensitivity and miniaturization in spaceborne environment where the atomic weightlessness effectively reduce the risk of running up against the instrument wall and significantly increase the interference time. At present, although the development of the on-ground experiment of the atom interferometry gradiometer has been matured, its space application has not been realized yet. In this paper, a measurement method suitable for space micro-gravity environment is proposed and discussed for the atom interferometry gravity gradiometer. The analysis results show that the precision of space-borne atom interferometry gravity gradiometer can achieve 1 mE/Hz1/2in the ＜0.1 Hz bandwidth which is concerned by satellite gravity gradiometry. The proposed measurement method can provide technical basis for the space application of the atom interferometry gravity gradiometer in the future.

atom interferometry; gravity gradiometer; space-borne; noise

1005-6734(2017)04-0449-06

10.13695/j.cnki.12-1222/o3.2017.04.005

P223. 6

A

2017-04-14；

2017-07-24

国家自然科学基金（41504034）

祝竺（1985—），女，博士，工程师，从事空间惯性传感器研究。E-mail: annieapple1985@sina.com