旋转调制式惯导系统隔离载体运动算法
孙伟强,曹 东,戚嘉兴,刘 伟,张灵妍
(1. 天津航海仪器研究所,天津 300131;2. 中国人民解放军72433部队自动化工作站,济南 250014)
旋转调制式惯导系统隔离载体运动算法
孙伟强1,曹 东1,戚嘉兴2,刘 伟1,张灵妍1
(1. 天津航海仪器研究所,天津 300131;2. 中国人民解放军72433部队自动化工作站,济南 250014)
旋转调制式惯导系统中,转位运动受载体运动的影响,误差调制效果受影响。针对这一问题,提出基于载体姿态角解耦的隔离载体运动算法。首先建立载体运动姿态角与旋转机构之间的数学关系,然后设计了隔离载体运动的力矩信号施加量的实时解耦算法,最终推导了隔离载体运动力矩信号的公式,完成了载体运动隔离算法的设计。数字仿真结果表明,通过该算法,可以降低载体运动对误差调制规律的影响。跑车试验结果表明,通过隔离载体运动算法的应用,转向对系统定位误差影响由不隔离载体运动时约0.5 nm降低到了基本为0 nm。
旋转调制;捷联惯性导航系统;隔离载体运动;姿态角解耦算法
旋转调制式惯导系统通过对 IMU的旋转来调制惯性元件的误差[1-6]。IMU的角运动实际是系统转位运动与载体运动两种运动的复合,而真正起到误差调制作用的是相对于地理坐标系的系统转位运动,如果不隔离载体运动,二者混在一起,将大大影响动态条件下的误差调制效果[7-10]。
针对这一问题,本文提出基于载体姿态角解耦的载体运动隔离算法,研究载体姿态角变化与旋转机构之间的关系,设计载体运动姿态角的实时解耦算法,形成载体运动隔离算法,并进行仿真和跑车试验。
1 姿态角解耦原理及算法
1.1 姿态角解耦原理
提取的载体姿态角是载体在当地地理坐标系中的三维角度。与IMU固连的台体相对于导航坐标系在不断进行转位和停止运动,在停止时台体相对于当地地理坐标系保持静止。某型惯性导航系统的框架配置示意图如图 1所示:最内部的椭圆形表示惯性测量组件,称之为台体;与台体相连的框架称之为内框,与内框和外部相连的为外框;转位机构即电机的轴分别位于台体轴、内框轴和外框轴上。从图 1中可以看出,由于转位运动的存在,陀螺仪的输入轴是在不断变化的,使得陀螺仪输入轴和装在框架轴上的电机轴不平行,因而所需绕陀螺仪输入轴的运动必需由绕三根框架轴的运动来保证。

图1 某型惯性导航系统框架配置示意图Fig.1 Frame configuration of an inertial navigation system
1.2 姿态角解耦算法
台体坐标系输入轴的运动是已知的,求取绕三根架轴的运动与平台式系统类似,通过以下推导获取。设为与载体固连的坐标系,为与外框架固连的坐标系,为与内框架固连的坐标系,为与台体固连的坐标系。定义外框轴读角为k,内框轴读角为ψ,台体轴读角为θ,则经过以下规则变换可变换为绕轴正向旋转k角得外框架坐标系转换矩阵记为绕Xo轴正向旋转ψ角得内框架坐标系转换矩阵记为绕YI轴旋转θ角得台体坐标系转换矩阵记为根据旋转坐标系之间的关系,有:

从而得到台体坐标系与载体坐标系之间的关系为:
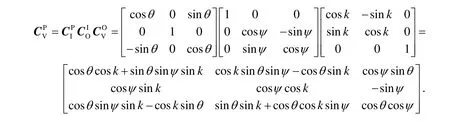
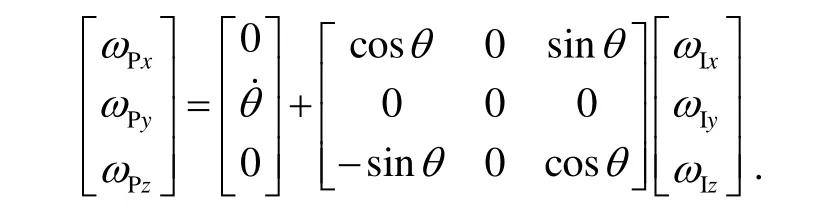
内框坐标系各轴角速度与外框坐标系各轴角速度之间有如下关系:

从而有:
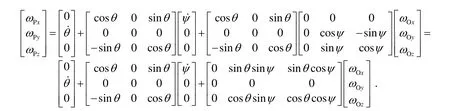
根据定义,三只电机分别在外框坐标系的OZ、内框坐标系的OX轴以及台体坐标系的OY轴上,而需要求取的关系为:在已知台体坐标系各轴角速度的情况下,推导出其与三只电机角速度之间的转换关系。考虑到则有:
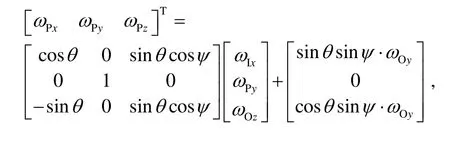
三只电机构成的坐标系记为S系,为非正交坐标系,则有:
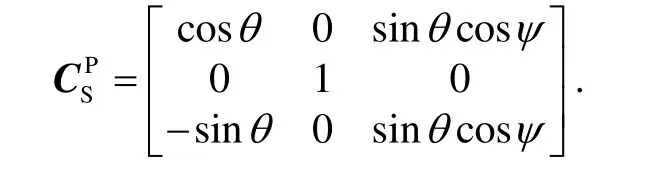
对其求逆,即可得到台体坐标系到电机坐标系之间的转换矩阵为:
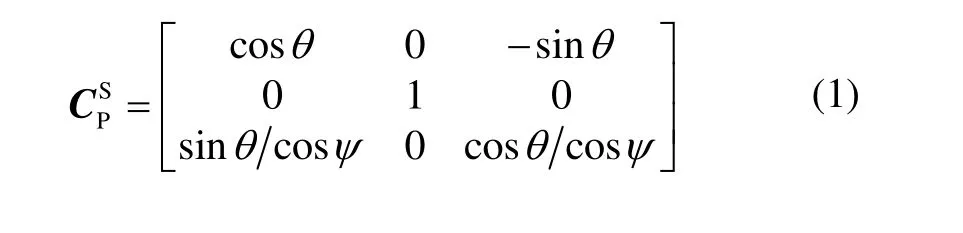
即:
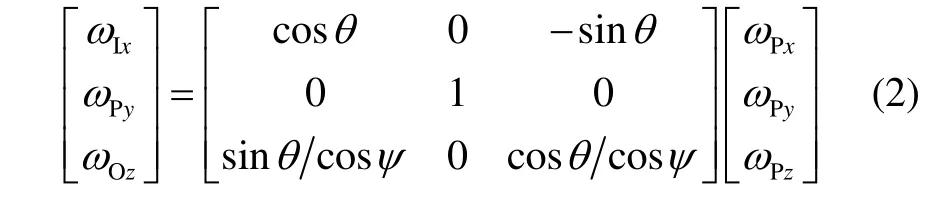
式(2)的关系可以用图2来表示。采用图2所示的关系可以将台体轴上陀螺仪的角速度转换到三个轴的电机的角速度。
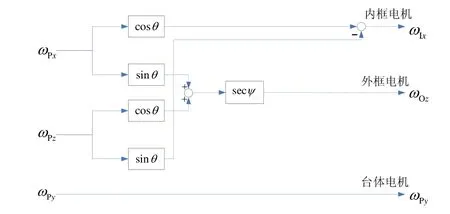
图2 力矩信号解耦关系图Fig.2 Decoupling relationship of the moment signals
2 隔离载体运动算法设计及仿真
2.1 隔离载体运动算法设计
根据以上研究,对旋转调制式系统隔离载体运动算法进行了设计分析,最终确定了旋转调制式系统隔离载体运动算法。
陀螺仪能感受到载体相对于惯性空间的运动。将陀螺仪的输出经过解调、校正、调制及功率放大后,反馈输入给框架轴上的力矩电机,产生恢复力矩,直接或通过减速器以平衡作用于载体运动的干扰,保持框架角方位相对于惯性空间保持不变,给框架电机施加力矩的公式如式(3)所示,由于框架角方位相对于惯性空间保持不变,这就是惯性稳定平台的工作原理。

舰船惯性导航系统通常采用半解析式系统的方案,相对于惯性平台式系统的工作原理,半解析式系统的台体需要跟踪当地地理坐标系,规定当地地理坐标系为东、北、天坐标系,当地地理系的角速率通过姿态转换矩阵可以投影到台体坐标系上,姿态转换矩阵由系统的捷联解算提供,则当系统稳定在当地地理坐标系下时,力矩电机的施加力矩如式(4)所示:
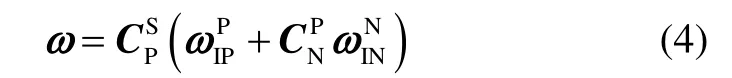
误差调制式系统中的转位方案是相对于导航坐标系进行设计编排的,陀螺仪和加速度计只有相对于导航坐标系按转位方案进行旋转,才能够达到误差调制的效果。在误差调制式惯导系统中,采用了当地地理坐标系作为导航坐标系,由于陀螺仪与加速度计与台体坐标系固连,因此陀螺仪与加速度计的转位规律即台体的转动角速率,记为wa,则误差调制式系统的隔离载体运动算法如式(5)所示:
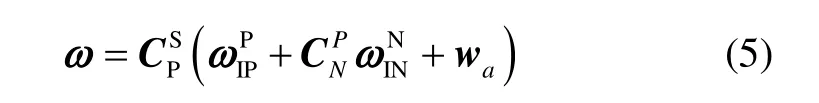
2.2 隔离载体运动算法仿真试验
上面对基于姿态角解耦的隔离载体运动算法的原理及方法给出了细致的阐述说明,本节针对提出的隔离载体运动算法进行仿真验证试验。仿真试验模型中包括载体运动环境的模拟、误差调制式系统陀螺仪与加速度计数据生成的模型、捷联解算以及姿态角提取模型、隔离载体运动算法模型,仿真框图如图3所示。

图3 隔离载体运动算法仿真框图Fig.3 Simulation frame of carrier movement isolation algorithm
图4~6依次为无摇摆旋转调制系统z轴陀螺仪输出曲线、有摇摆无隔离旋转调制系统z轴陀螺仪输出曲线和有摇摆有隔离旋转调制系统z轴陀螺仪输出曲线。通过对比可以看出,通过引入隔离载体运动算法,外界运动对陀螺仪输出影响基本隔离掉了,保证了旋转调制规律。

图4 无摇摆陀螺输出曲线Fig.4 Gyro output without swing
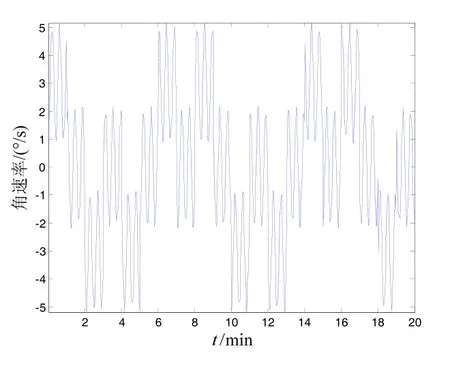
图 5 有摇摆未隔离时陀螺输出曲线Fig.5 Gyro output with swing and without isolating

图6 有摇摆采取隔离陀螺输出曲线Fig.6 Gyro output with swing and isolating
3 试验验证
采用隔离载体运动算法,在某型旋转调制式惯性导航系统中进行了跑车试验进行验证,试验采用同一套旋转式系统,试验车辆也为同一辆。试验过程为:对准完成后开始进行导航,导航过程中载体有运动变化,结果如图7和图8所示。图中分别给出了未采用隔离方案和采用隔离方案的定位结果与航向变化的对比,从中可以看出:未采用隔离运动方案时,载体转向机动约对定位结果有0.5 nm的影响;采用隔离运动方案后,载体机动对系统定位结果基本无影响。隔离载体运动方案大大提高了系统的动态适应性能。

图7 未隔离定位误差与航向曲线Fig.7 Positioning error and heading without isolating
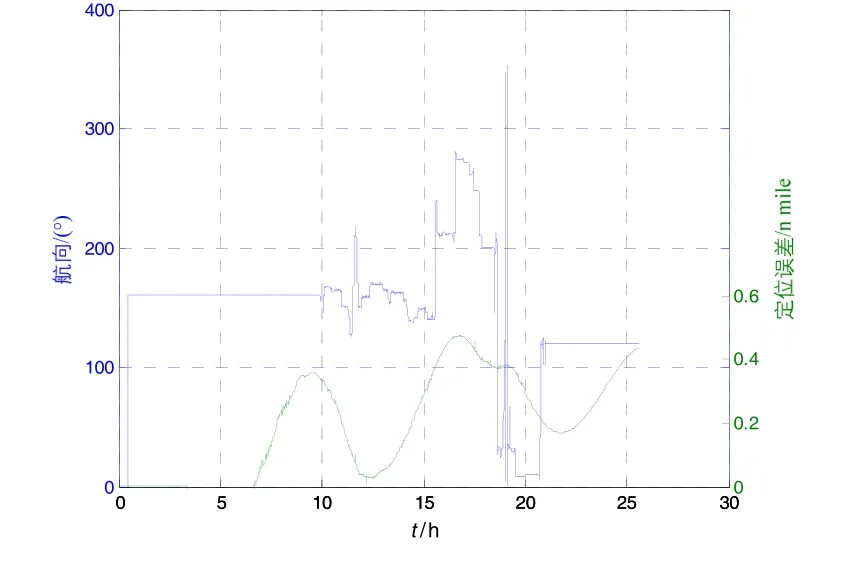
图 8 隔离载体运动定位误差与航向曲线Fig.8 Positioning error and heading with isolating
4 结 论
通过数字仿真和跑车试验验证,说明所设计的基于姿态角解耦的载体运动隔离算法可以实现旋转调制式惯导系统中对载体运动的隔离,保证误差调制规律的实现,提高系统定位精度。
(References):
[1]Yin H L, Yang G L, Song N F, et al. Error modulation scheme analyzing for dual-axis rotating fiber-optic gyro inertial navigation system[J]. Sensor Letters, 2012, 10(7):1359-1363.
[2]Song N F, Cai Q Z, Yang G L, et al. Analysis and calibration of the mounting errors between inertial measurement unit and turntable in dual-axis rotational inertial navigation system[J]. Measurement Science and Technology, 2013,24(11): 115002-1-115002-10.
[3]Tucker T, Levison E. The AN/WSN-7B marine gyrocompass navigator[C]//Proc. of the National Technical Meeting of the Institute of Navigation. 2000: 348-357.
[4]Chang Guo-bin, Xu Jiang-ning, Li An, et al. Error analysis and simulation of the dual-axis rotation-dwell autocompensation strapdown inertial navigation system[C]//International Conference on Measuring Technology and Mechatronics Automation. 2010.
[5]Levinson E, Majure R. Accuracy enhancement techniques applied to the marine ring laser inertial navigator (MARLIN)[J]. Journal of The Institute of Navigation, 1987, 34(1):64-85.
[6]Ishibashi S, Tsukioka S, Yoshida H. Accuracy improvement of an inertial navigation system brought about by the rotational motion[J]. Oceans, 2007, 25(10): 1-5.
[7]唐江河, 李文耀, 詹双豪, 等. 一种外环水平结构双轴光纤惯导系统旋转方案设计方法[J]. 导航定位与授时,2016, 4(3): 1-8.Tang Jiang-he, Li Wen-yao, Zhan Shuang-hao, et al.Rotation scheme design method for dual-axis ins with horizontal outer-axis structure[J]. Navigation Positioning and Timing, 2016, 4(3): 1-8.
[8]常国宾, 许江宁, 李安, 等. 载体运动对双轴连续旋转调制式惯导方案误差的影响[J]. 中国惯性技术学报,2011, 19(2): 175-179.Chang Guo-bin, Xu Jiang-ning, Li An et al. Influence of body dynamics on the error of INS scheme with dual-axis continuous autocompensation technique[J]. Journal of Chinese Inertial Technology, 2011, 19(2): 175-179.
[9]张伦东, 练军想, 胡小平. 载体角运动对旋转式惯导系统旋转调制效果的影响[J]. 国防科技大学学报, 2011,33(4): 152-156.Zhang Lun-dong, Lian Jun-xiang, Hu Xiao-ping. The effect of vehicle angle motion on rotation modulation technology for rotating INS[J]. Journal of National University of Defense Technology, 2011, 19(2): 175-179.
[10]覃方君, 李安, 徐江宁. 载体角运动对旋转调制惯导系统误差影响分析[J]. 武汉大学学报(信息科学版), 2012,37(7): 831-833.Qin Fang-jun, Li An, Xu Jiang-ning. Analysis of errors of rotating modulation ins effected by angular motion of vehicle[J]. Geomatics and Information Science of Wuhan University, 2012, 37(7): 831-833.
[11]王国臣, 袁保伦, 饶谷音, 等. 激光陀螺双轴旋转导航系统高精度转动控制的设计与实现[J]. 中国惯性技术学报, 2015, 23(4): 438-441.Wang Guo-chen, Yuan Bao-lun, Rao Gu-yin, et al. Highprecision rotating scheme for laser gyroscope dual-axis rotating inertial navigation system[J]. Journal of Chinese Inertial Technology, 2015, 23(4): 438-441.
Carrier movement isolation algorithm for rotary-modulation inertial navigation system
SUN Wei-qiang1, CAO Dong1, QI Jia-xing2, LIU Wei1, ZHANG Ling-yan1
(1. Tianjin Navigation Instrument Research Institute, Tianjin 300131, China;2. Automation Station in Unit 72433 of PLA, Jinan 250031, China)
In rotary-modulation INS (inertial navigation system), the rotary modulation effect is affected by the carrier movement. An algorithm for isolating the carrier movement was brought up to solve this problem.First, the mathematical relationship between the carrier movement attitude angles and the executing components was established. Then the real-time decoupling algorithm of the moment signals for isolating the movement was designed. At last, the formula for isolating the moment signals of the carrier movement was derived, and the design of the carrier movement isolation algorithm was finished. Numerical simulations verify that this algorithm could reduce the influence of the carrier movement on the rotary modulation. The vehicle running experiment shows that, with this algorithm, the positioning error caused by the turning is reduced to almost 0 nm from 0.5 nm.
rotary modulation; strapdown inertial navigation system; carrier movement isolation; attitude decoupling algorithm
1005-6734(2017)04-0432-04
10.13695/j.cnki.12-1222/o4.2017.04.002
U661.1
A
2017-04-27;
2017-07-27
装备预先研究项目(3020107010202)
孙伟强(1984— ),男,工学硕士,高工,从事捷联式惯性导航系统研究。E-mail: sunwq1984@163.com

