中心力场质点机械能及机械能与离心率之间关系的简洁推导

曾卓全，潘孟美，王红晨

(海南师范大学 物理与电子工程学院, 海南 海口 571158)

中心力场质点机械能及机械能与离心率之间关系的简洁推导

曾卓全，潘孟美*，王红晨

(海南师范大学 物理与电子工程学院, 海南 海口 571158)

文章基于比耐(Binet)公式和近日点的机械能导出轨道离心率e和机械能E之间的关系式，同时还推导了不同轨道上质点机械能E的表达式.该方法通俗易懂，避免了复杂的积分运算，便于学生更好地理解中心力场质点轨道运动的问题.

有心力场; 离心率; 机械能; 比耐公式; 圆锥曲线

对于力学问题，在已知质点受力的情况下可以通过牛顿第二定律求出质点的运动规律，即质点的位置和时间的关系.行星绕太阳运动的问题可以简化为质点在有心力作用下运动的问题.在有心力的问题中，如何求解质点在中心力场中的运动轨道，是大学本科《理论力学》课程的重点与难点，不少初学者对这个问题理解比较吃力.教科书对有心力场问题的处理是从运动规律中消去时间t，得到r和θ的微分方程，再求解该微分方程从而得到轨道方程[1].但是该求解过程没有给出轨道方程中的积分常数A，而是从两个首次积分出发推导轨道离心率e和系统机械能E之间的关系式，这个方法的关键是要计算一个比较复杂的积分.从两个首次积分出发，构造质点轨道的常微分方程，利用积分公式得到轨道方程，这无疑是大学生应具备的基本能力.但从课程教学法的角度来说，如果能一题多解，能从不同角度看待这个问题，有益于增进学生对该问题的理解.本文利用轨道中的一些特殊点(远日点、近日点)，通过一些简单的代数运算，直接确定轨道离心率e和系统机械能E之间的关系，还给出积分常数A的具体表达式；同时，还研究了行星在不同轨道上的能量.

1 行星运动轨道方程

在行星绕太阳运动的问题中，行星所受的太阳引力与距离的平方成反比.欲求行星的轨道方程，通常先求运动规律，然后再从运动规律中把时间参数t消去,得到u和θ的微分方程，即比耐公式[1]：

(1)

将F=-mk2u2代入(1)式化简得：

.

(2)

解方程(2)得

(3)

式中A及θ0为常数，最后得到轨道方程：

(4)

如果把极轴转过一个角度，可使θ0=0，(4)式简化为

(5)

常数A由体系的机械能E和比角动量h决定.把(5)式和极坐标系下圆锥曲线的基本方程

(6)

相比较得

(7)

其中，p为圆锥曲线正焦弦长度的一半，e为轨道偏心率.

教材[1]并没有由此定出常数A，而是从另外一个角度得到e与E的关系式(别的一些教材也是这样处理的[2-4]).即：利用两个首次积分(角动量守恒、机械能守恒)，消去时间t，得到r和θ的微分方程，通过求解该微分方程得出轨道方程.将所得轨道方程与(6)式比较就能得到机械能(E)和偏心率(e)的关系式，与(5)式比较就能得到A与能量的关系式.具体过程简述如下.机械能守恒定律为

(8)

为能和角动量守恒结合起来，作如下变量代换

把上式代入(8)式中，得

两边积分，得到质点的轨道方程，

(9)

取θ0=0，再与标准表达式(6)式比较，从而确定离心率

(10)

这个方法的关键是要计算一个比较复杂的积分.本文将利用轨道中的一些特殊点(远日点和近日点)，通过一些简单的代数运算，直接确定离心率.

2 机械能与离心率之间关系的简洁推导及行星椭圆运动的周期

由机械能守恒定律

(11)

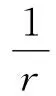
(12)

对轨道方程(3)考虑近日点(θ=0)，

(13)

将(13)式代入(12)式化简得

(14)

从中解出常数A，

(15)

将(15)式代入轨道方程(4)得：

(16)

比较圆锥曲线的基本方程(6)得离心率与机械能的关系：

(17)

(18)

虽然角动量不影响轨道类型，但影响轨道的偏心率.对于椭圆，角动量大则偏心率小，对于双曲线，角动量大则偏心率大.

对于作椭圆轨道运动的行星，还可计算其运动周期.设S是矢径扫过的面积，有

(19)

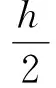
(20)

(21)

即：行星公转周期的平方与轨道半长轴的立方之比值是一个与行星无关的常数.

3 行星在不同轨道上的能量

本节计算行星在三类圆锥曲线(椭圆、抛物线、双曲线)轨道上的能量.

3.1行星在椭圆轨道上的能量

化简(11)式得

(22)

(23)

由(18)式有

(24)

下面用两种方法计算行星在椭圆轨道上的能量.

方法一.椭圆轨道近日点的径向坐标为r1=a-c.把r1=a-c和(18)式代入(24)式，化简得

(25)

比较(24)式与(25)式就得到行星在椭圆轨道上的机械能：

(26)

所以，体系的机械能决定椭圆轨道的半长轴.

方法二.椭圆轨道近日点(径向坐标为r1=a-c)到远日点(径向坐标为r2=a+c)的距离为r1+r2=2a.从(24)式，即

(27)

得到两根之和为

(28)

所以，行星在椭圆轨道上的机械能为：

(29)

3.2行星在抛物线轨道上的能量

(30)

所以，行星在抛物线轨道上的能量E=0.

3.3行星在双曲线轨道上的能量

双曲线轨道近日点(r1=c-a)，把r1=c-a和(18)式代入(24)式，化简得

(31)

比较(24)式与(31)式得行星在双曲线上的机械能为：

(32)

4 结论

本文基于比耐公式和近日点的机械能导出了行星的轨道偏心率e和机械能E之间的关系式，同时还推导了不同轨道上行星机械能E的表达式及行星作椭圆轨道运动的运动周期.文中所有的推导过程简单易懂，避免了繁杂的积分运算，能增进学生对求解质点在中心力场中运动的轨道问题的理解.同时，本文提供的方法对学生把握、运用远日点、近日点的性质去处理类似问题也是有益的.

[1] 周衍柏. 理论力学教程[M]. 第3版. 北京：高等教育出版社，2009.

[2] 梁昆淼. 力学：下册[M]. 第4版. 北京：高等教育出版社，2009.

[3] 金尚年, 马永利. 理论力学[M]. 第2版. 北京：高等教育出版社，2002.

[4] Morin D. Introduction to classical mechanics with problems and solutions[M]. Cambridge：Cambridge University Press, 2007.

[5] Goldstein H, Poole C, Safko J. Classical mechanics[M]. 3rd ed. New York：Pearson Education, 2002.

AConciseDerivationoftheParticle’sMechanicalEnergyandtheRelationbetweenEccentricityandMechanicalEnergyintheCentralForceField

ZENG Zhuoquan，PAN Mengmei，WANG Hongchen

(SchoolofPhysicsandElectronicEngineering,HainanNormalUniversity,Haikou571158,China)

The article derives the relation between the eccentricity e and mechanical E on the Binet formula and the mechanical energy of the perihelion, and also derives the formula of the particle’s mechanical energyEin different orbit. This method is easy to understand, avoiding the complex integral operation, and enhance students’ understanding of the problem.

central force field; eccentricity; mechanical energy; Binet formula; conic section

G 420；O 311.1

A

1674-4942(2017)03-0339-05

2017-03-21

海南省自然科学基金(20165196)

潘孟美，副教授，E-mail：panmengmei01@163.com

10.12051/j.issn.1674-4942.2017.03.016

责任编辑：吴兴华