利用微分算子法研究二阶齐次线性微分方程与Riccati方程通解之联系

林庆泽

(广东工业大学 应用数学学院, 广东 广州 510520)

利用微分算子法研究二阶齐次线性微分方程与Riccati方程通解之联系

林庆泽

(广东工业大学 应用数学学院, 广东 广州 510520)

文章应用微分算子法处理二阶变系数线性微分方程，揭示了二阶齐次变系数线性微分方程与Riccati方程的通解理论之间的联系，发现这两类方程之间的通解可以互相转化，同时给出转化的途径.最后，作为理论的应用分析了一些具体例子.

算子法;微分方程;Riccati方程;通解

对Riccati方程进行的许多研究的重要动机是很多物理问题涉及的方程与其密切相关.比如，量子力学中的Schrödinger方程常常可化为Riccati方程的形式[1].然而Riccati方程的非线性性为其求解带来了极大的难度.已有很多文献对满足一些特定条件的Riccati方程给出了解析的或者数值的解法.如文献[2]给出了具有多项式系数的Riccati方程的扭结孤解，而文献[3]则给出了具有有理函数系数的Riccati方程的有理解.近年来，一些新的研究方法，如Adomian分块方法和He变分迭代法等，被用于Riccati方程的研究并取得了很多成果[4,5].

微分算子法是近代发展起来的一种以代数观点处理分析问题的重要方法.著名数学家Hormander L在其长达4卷的名著中对线性偏微分算子做出了极为系统的论述，特别是在偏微分方程一般理论上取得了一系列突破性的成果[6].

文献[7]利用微分算子法研究了二阶常系数线性微分方程

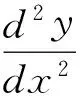
(1)

的通解理论.根据该微分方程的特征方程λ2+pλ+q=0的根的取值情况，得出了如下三种通解的积分表示.

1.若r1，r2是特征方程的两不相等的实根，则通解表达式为

(2)

2.若r1=r2=r是特征方程的重根，则通解表达式为

(3)

3.若特征方程无实根，即p2-4q<0时，该特征方程有两个复根

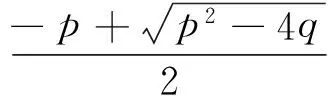
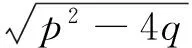
(4)

注：文献[7]对(4)式的表述存在着错误：漏写了几项.这里给出了改正.

本文在此基础上，将该微分算子法应用于二阶变系数线性微分方程的求解理论，揭示了二阶齐次变系数线性微分方程与Riccati方程的通解理论之间的联系，获得了这两类方程之间的通解可以互相转化的结论并给出一些例子作为应用.

1 算子法处理变系数线性微分方程的通解理论

对于一般的二阶变系数线性微分方程:

(5)

我们使用微分算子法将方程(5)化为下面的形式：

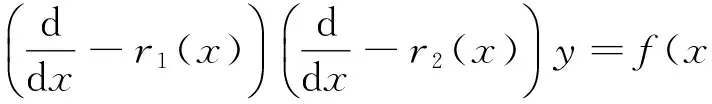
(6)

将(6)式展开成：

(7)

对照(5)式和(7)式，于是r1(x),r2(x)必须满足：

(8)

于是，根据微分算子方程(6)，求解方程(5)就等价于解一阶线性微分方程组：

(9)

而(9)中第一个方程的通解为

(10)

故求解方程组(9)等价于求解一阶线性微分方程：

(11)

因此二阶变系数线性微分方程(5)的通解为：

(12)

其中r1(x),r2(x)由方程组(8)决定.

而二阶变系数线性微分方程(5)对应的齐次线性微分方程的通解则为：

(13)

其中r1(x),r2(x)也由方程组(8)决定.

2 二阶变系数线性微分方程与Riccati方程的联系

由前面的推导可知，要求出二阶变系数线性微分方程(5)的通解，求解方程组(8)是一个非常关键的步骤.下面将证明：求解方程组(8)相当于求解一个Riccati方程.

由方程组(8)的第一个方程得到：r1(x)=-p(x)-r2(x).将其代入方程组(8)的第二个方程，得到：

(14)

方程(14)是一个Riccati方程[8,9].

于是我们得到：

定理1 若r2(x)是Riccati方程(14)的一个特解，令r1(x) =-p(x)-r2(x)，则二阶变系数线性微分方程(5)的通解由(12)表示.

现在反过来考虑，如何从二阶齐次线性微分方程的非零特解来推出对应的Riccati方程的通解呢？我们证明以下定理：

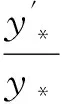
证明由方程(11)和公式(12)，

(15)

由于我们考虑的y*是二阶齐次线性微分方程的一个特解，故f(x)≡0，且其中C，C1都是确定的常数,从而，

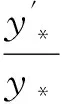
(16)

下面检验(16)是否是Riccati方程(14)的一个特解.记

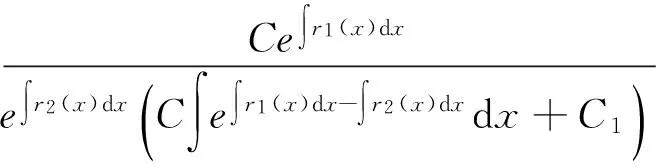
(17)

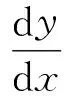
(18)

的两边并观察等式是否成立.此时代入后的方程(18)转化为

=-q(x)-p(x)r2(x)-(r2(x))2-(p(x)+2r2(x))H(x)-(H(x))2.

(19)

由于r2(x)是Riccati方程(14)的一个特解，所以方程(19)等价于

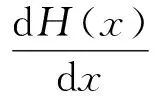
(20)

将(17)式代入到方程(20)，此时方程(20)两边都等于

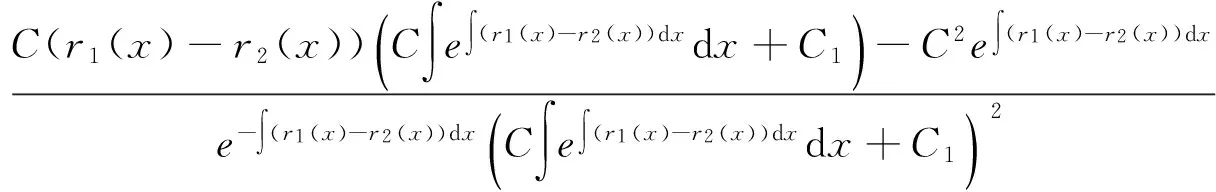
由定理2可知，若知道二阶变系数线性微分方程(5)对应的二阶齐次线性微分方程的一个非零特解，则我们能够给出其对应的Riccati方程(14)的一个特解.下面的定理告诉我们，若给出Riccati方程(14)的一个特解，我们就能够给出Riccati方程(14)的通解.

定理3[9,10]若y0是Riccati方程(14)的一个特解，则Riccati方程(14)的通解为：

(21)

证明若r2(x)是Riccati方程(14)的一个特解，令r1(x)=-p(x)-r2(x)，则可由定理2及(16)式知，函数

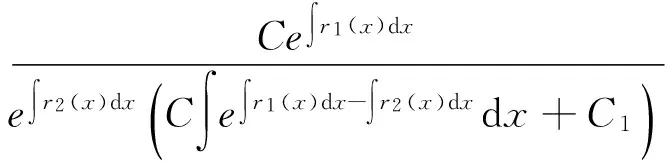
(22)

是Riccati方程(14)的通解.将r2(x)=y0及r1(x)=-p(x)-r2(x)代入(22)式右边，即得Riccati方程(14)的通解为

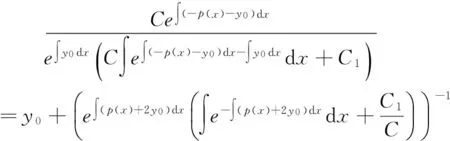
(23)

因此，Riccati方程(14)的通解即为(21)式.证毕.

Riccati方程(14)中(r2(x))2项的系数为-1，而对于一般的Riccati方程

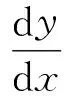
(24)

其中k(x)是连续可微的，我们有下面的定理：

定理4 对于一般的Riccati方程(24)，我们总是可以通过变换：g(x)=-k(x)y将方程(24)化为方程(14)的形式.

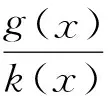
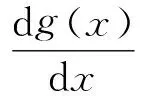
(25)

方程(25)即为方程(14)的形式.证毕.

3 应用举例

1.对于一般的常系数Riccati方程

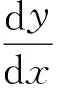
(26)

我们可以按照定理4做变换g(x)=-ky，将方程(26)化为方程(14)的形式：

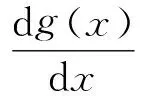
(27)

现在将Riccati方程(27)的求解转化为求解其对应的二阶齐次线性微分方程

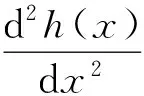
(28)

例1 求解常系数Riccati方程

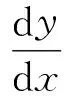
(29)

解作变换g(x)=-3y，方程(29)化为

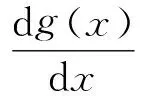
(30)

方程(30)对应的二阶齐次线性微分方程为

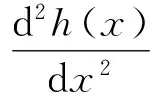
(31)

方程(31)的特征方程λ2-2λ+3=0无实根，有两个复根：

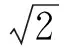
因此由(4)式，方程(31)的通解为：

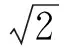
则由定理2，方程(30)的通解为：

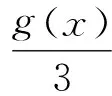
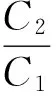
2.对于任意一个连续可微函数r2(x)，我们都可以找到无穷多个不同的Riccati方程，使得这些方程都以r2(x)为其特解.证明如下：

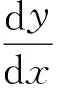
(32)

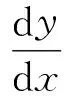
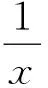
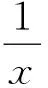
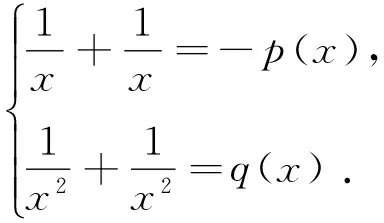
例3 求解二阶线性微分方程：

(33)

解方程(33)对应的Riccati方程为

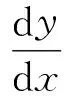
(34)

显然函数y=x为方程(34)的一个特根，故可令r2(x)=x，则r1(x)=x-x=0.因此根据定理1可知方程(33)的通解为：

4 结论

本文首先利用文献[7]中的微分算子法处理了二阶变系数线性微分方程，得出了其通解的积分表示形式.其次，本文揭示了微分算子方程的构造与对应的Riccati方程的关联性，从而由定理1、定理2、定理3和定理4得出了二阶齐次变系数线性微分方程与Riccati方程的求解问题可以互相转化的重要结论并给出了转化的途径.文中最后将常系数Riccati方程的通解问题转化为二阶常系数齐次线性微分方程的通解问题，而后者的解法完全由(2)、(3)和(4)式给出.

[1] Landau L D, Lifshitz E M. Quantum mechanics: non-relativistic theory, Volume 3[M]. 3rd ed. Beijing: Beijing World Publishing Corporation, 1999.

[2] Navickas Z, Ragulskis M, Marcinkevicius R, et al. Kink solitary solutions to generalized Riccati equations with polynomial coefficients[J]. Journal of Mathematical Analysis and Applications, 2017, 448(1): 156-170.

[3] Echi N. Rational solutions of Riccati differential equation with coefficients rational[J]. Applied Mathematics and Computation, 2012, 218(21): 10341-10366.

[4] Eltawil M A, Bahnasawi A A, Abdel-Naby A. Solving Riccati differential equation using Adomian’s decomposition method[J]. Applied Mathematics and Computation, 2004, 157(2): 503-514.

[5] Abbasbandy S. A new application of He’s variational iteration method for quadratic Riccati differential equation by using Adomian’s polynomials[J]. Journal of Computational and Applied Mathematics, 2007, 207(1): 59-63.

[6] Hormander L. The analysis of linear partial differential operators, Volume I-IV[M]. New York: Springer, 2005.

[7] 林庆泽. 算子法在处理线性微分方程中的应用[J]. 兰州文理学院学报(自然科学版), 2016, 30(1): 13-16.

[8] 丁同仁, 李承治. 常微分方程教程[M]. 北京: 高等教育出版社, 2004.

[9] Reid W T. Riccati differential equations[M]. New York: Academic Press, 1972.

[10] Scott M R. Invariant imbedding and its applications to ordinary differential equations:an introduction[M]. London: Addison-Wesley, 1973.

StudyontheRelationbetweentheGeneralSolutionsoftheSecondOrderHomogeneousLinearDifferentialEquationandtheOnesofRiccatiEquationbyDifferentialOperatorMethod

LIN Qingze

(SchoolofAppliedMathematics,GuangdongUniversityofTechnology,Guangzhou510520,China)

The second-order linear differential equations with variable coefficients are processed by differential operator method, and the relation between the general solutions of the second-order homogeneous linear differential equations with variable coefficients and the ones of Riccati equations is revealed. Then, the conclusion that the general solutions between the two equations can be transformed into each other is deduced and the way of transformation is given. Finally, some examples are given as theoretical applications.

operator method; differential equation; Riccati equation; general solution

O175

A

1674-4942(2017)03-0237-06

2017-01-14

林庆泽，硕士，E-mail：gdlqz@e.gzhu.edu.cn

10.12051/j.issn.1674-4942.2017.03.001

责任编辑：吴兴华