引信气流激振压电发电机结构参数影响分析

邹华杰， 张江华， 陈荷娟， 王泽平

(1.常州机电职业技术学院 机械工程学院， 江苏 常州 213164；2.南京理工大学 机械工程学院， 江苏 南京 210094)

引信气流激振压电发电机结构参数影响分析

邹华杰1,2， 张江华1， 陈荷娟2， 王泽平1

(1.常州机电职业技术学院 机械工程学院， 江苏 常州 213164；2.南京理工大学 机械工程学院， 江苏 南京 210094)

满足引信用小型振动压电发电机气流致振发电要求，解决稳定激振力的问题，控制结构敏感参数是一种有效方法。通过模拟吹风实验，分析气流致声激振机构的相关结构参数对激振力的影响规律。结果表明，不同共振腔长度对应的激振力幅值与入流速度近似呈现线性增大趋势，且长度越大其斜率越小，反之亦然，喷口到共振腔的间距和喷口环隙对激振力幅值的影响较复杂，过大或过小都会使得激振力幅值较小甚至没有波形产生；共振腔长度是影响激振力频率的主要因数，频率随长度的增大而变小，呈现反比关系，喷口到共振腔的间距和喷口环隙对频率的影响较小。因此，对于高速气流，短共振腔可以获得较大幅值的高频稳定激振力，以及需合理控制喷口到共振腔的间距和喷口环隙使得激振力幅值较大。

兵器科学与技术； 引信； 气流致声； 压电发电机； 激振力

0 引言

随着弹药灵巧化和智能化的发展趋势，各种复杂微电子应用系统也需要持续自供电或作为其他能源的补充电源，越来越需要电磁兼容性好的小型物理电源。引信用气流激振压电发电机[1]是一种利用弹丸飞行过程中的迎面气流激励压电换能器振动而发电的引信物理电源，具有结构简单且没有活动部件等特点。因此，如果能够通过提高压电发电机的驱动性能来增加其输出功率，将具有极大的应用前景。

关于这类气流激振压电发电机，国内学者对其进行了相关研究。李映平等[1]对振动式压电换能机理、压电换能器的固有频率以及振动压电发电的原理性实验等进行了相关的研究。黎晖等[2]对这种气流激振压电发电机的压电片和谐振腔的固有频率进行了推导。雷军命等[3]在文献[1]的基础上，设计了直径为34 mm的换能器，研究了压电振子的谐振特性，对气流激振压电发电机的输出电压和输出功率进行了简单实验研究。徐伟等[4]结合微机电(MEMS)技术提出了一种引信用MEMS气流谐振压电发电机，并通过流体- 固体耦合分析和压电仿真分析，对压电片的振动位移响应以及发电机的输出电压进行了研究。何鹏[5]设计了具有气流调节功能的进气口，并对迎面气流进入管内的流场进行了分析。在文献[5]的基础上，邹华杰等[6]注重于气流致声激振过程，设计了一个基于环形喷嘴—共振腔结构的气流致声激振机构，并通过数值仿真和实验对其气流致声激励特性进行了研究，结果表明由于共振腔内驻波声场的存在，使得激振力呈稳定正弦振动。在文献[6]的基础上，Li[7]对喷注流场中旋涡脱落过程进行了分析。邹华杰等[8]对发电机中声管固定方法进行了分析。根据“频率泵浦”设计思想[9]，Zou等[10]设计了小型气流致声激振压电发电机结构，并对其激振力以及电输出特性进行了研究，结果表明激振力与输出电压幅值成正比，且频率一致，该发电机具有结构简单、体积小、振动频率高且没有活动部件等特点，适合小口径弹引信弹载物理电源。以上文献都是针对这种气流激振压电发电机的气流激振机理以及压电换能进行的研究，关于结构参数对激振力特性影响方面却鲜有相关的研究报告。

结构参数对共振腔内驻波共振特性起决定性作用，影响激振力的幅值和频率，进而影响发电机的输出特性。为了实现提供稳定激振力，关键是有效控制结构敏感参数。为此，本文的研究注重于气流致声激振过程，通过模拟吹风实验，分析气流致声激振机构的相关结构参数对激振力的影响规律，通过对比各种结构参数组合下的激振力，从而确定良好波形激振力的气流致声激励机构结构参数及其变化范围。

1 气流激振压电发电机结构及工作原理

图1所示为气流激振压电发电机的结构示意图，由气流致声激振机构和压电换能器组成，图中H为环隙，D为共振腔直径，X为环形喷口到共振腔的距离，L为共振腔长度。气流致声激振机构主要由环隙、喷注和共振腔(压电换能器封闭末端)组成。其中，环隙由进气道和阻塞构成；喷注是弹丸飞行时的迎面气流(即入流)进入环隙再出来后得到的稳定涡流，喷注遇到共振腔口部的边棱(尖劈)产生扰动而形成边棱音[11]。喷注边棱音是典型的反馈气流声源，其作用恰恰可以弥补喷注气流的损失，放大气流机械能。与风吹声不同的是反馈在这里起主要作用，由喷口发出的高速喷注在空腔内(共振腔前端)静止的空气中通过时，喷注的边界上因高速流与静止介质的接触，不断产生旋涡并向前推动，因此喷注不断变宽。一部分遇到共振腔口部(边棱)时发生反射回到喷口，激发更多旋涡；一部分进入共振腔内激发其腔体振动，并在底部(刚性底部)反射回喷口。在声源处(共振腔口部)同时存在正、负向声波，如果它们同相则振动加强，可以产生频率主要由共振腔长度决定的声波，即在共振腔内形成驻波，共振腔底部声压最大(压力波的波腹)。共振腔底部声压(即激振力)驱动压电换能器振动、输出电能，实现声能到电能的转换。

图1 气流致声激振压电发电机的结构示意图Fig.1 Schematic diagram of airflow-induced vibration piezoelectric generator

2 实验装置和方法

本实验以气流致声激振过程为研究对象，忽略温度、湿度以及来流等因素的影响，仅模拟管内气流的压力或速度环境。实验系统主要由气源模拟系统、压力测量系统和实验试件等组成，如图2所示。气源模拟系统主要由气罐、减压阀和流量计组成。压力测量系统主要由压力传感器和数据记录仪组成。

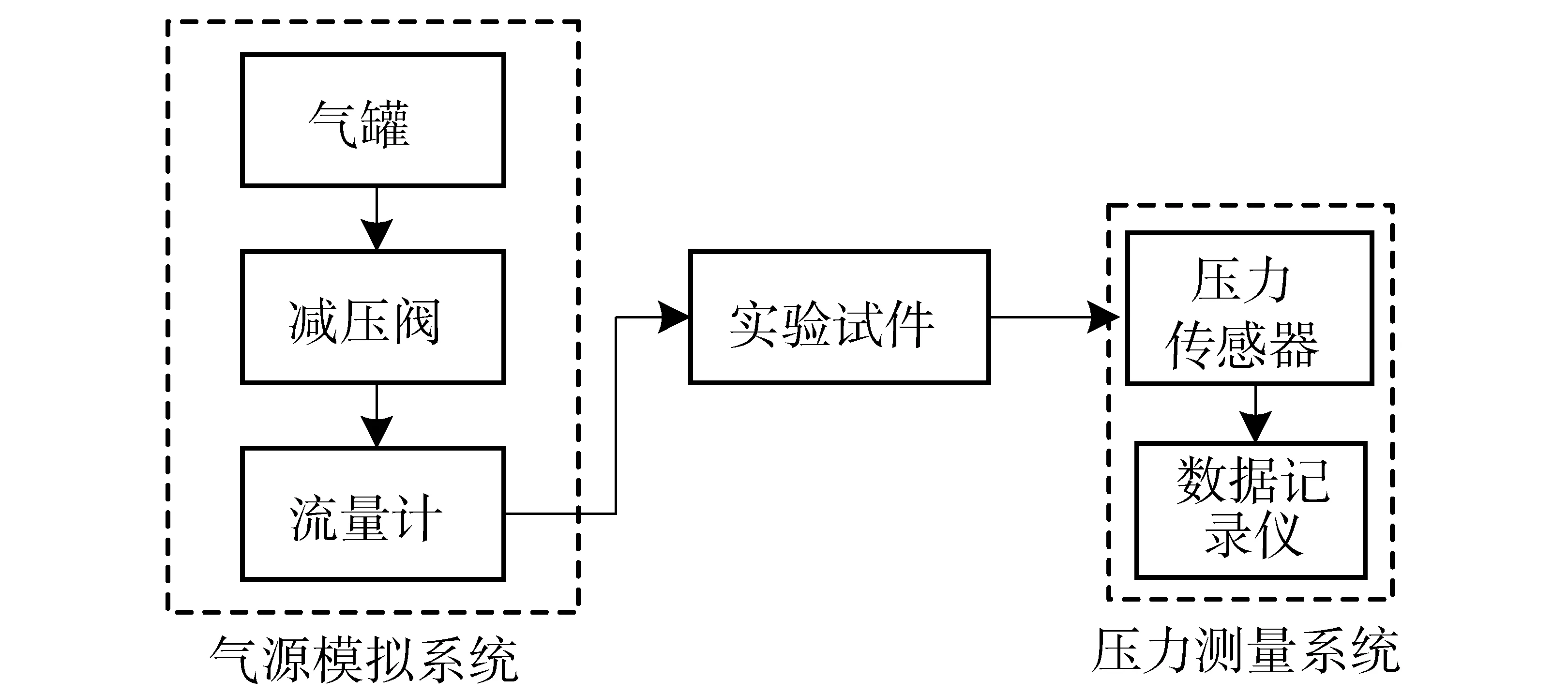
图2 实验系统框图Fig.2 Block diagram of experimental system

图3所示为实验照片。实验时，打开气罐，通过减压阀来调节进气口的气流大小，并通过流量计监测流量值；气流进入试件后，用压力传感器测量共振腔底部声压(激振力)，并用数据记录仪对相应数据进行记录。

图3 实验照片Fig.3 Experimental setup

实验所选取的气源流量范围为100～300 L/min，对应试件入口处的气流速度v与流量Q之间的表达式为

v=Q/S，

(1)

式中：v为气流速度；Q为流量；S为截面积。

3 结构参数影响实验分析

在进行气流致声激振机构的结构参数影响分析时，不考虑尖劈角度大小以及共振腔的壁厚，考虑的主要结构参数有4个，如图1所示，包括：1)共振腔长度L；2)共振腔直径D；3)间距X，即环形喷口到共振腔的距离；4)环隙H，即环形喷口的大小。将共振腔直径作为定值(D=10 mm)，其他3个参数作为可变值。

共振腔底部声压的变化能够直接反映气流激振压电发电机的激振力特性，针对气流致声激励机构的3个结构参数，开展共振腔底部声压曲线测量实验研究。为了全面了解结构参数对激振力的影响规律，分别对气流致声激励机构在某一单个参数不同取值条件下的实验测量结果进行分析，得到激振力变化规律曲线。

3.1 共振腔长度影响

为满足平面声波传播条件，将图1所示的共振腔设计为半封闭形式，当D=10 mm时，L应大于5 mm. 于是在分析长度对激振力的影响时，设计图1的实验样机如下：X=3 mm，H=1 mm，L分别为7 mm、10 mm、15 mm、20 mm. 激振力随时间的变化曲线以及对应的快速傅里叶变换(FFT)如图4所示，声压曲线都呈正弦波形状，幅值和频率都比较稳定。实验结果如下：

1)激振力幅值与流速呈现线性关系，如图5所示。在流速小于70 m/s时，随着流速的增大，L越小其激振力越小；在流速大于90 m/s时，随着流速的增大，L越小其激振力越大。

2)激振力频率与流速关系，如图6所示。L越大，频率偏差越小；当L=20 mm时，所对应的频率偏差值不大于157 Hz，相对误差为4.3%. 频率偏差值小，说明频率对流速不敏感。

根据以上分析可知，在较大流速情况下，为获得高频、大振幅的稳定激振力，可以选择尽可能短的共振腔。

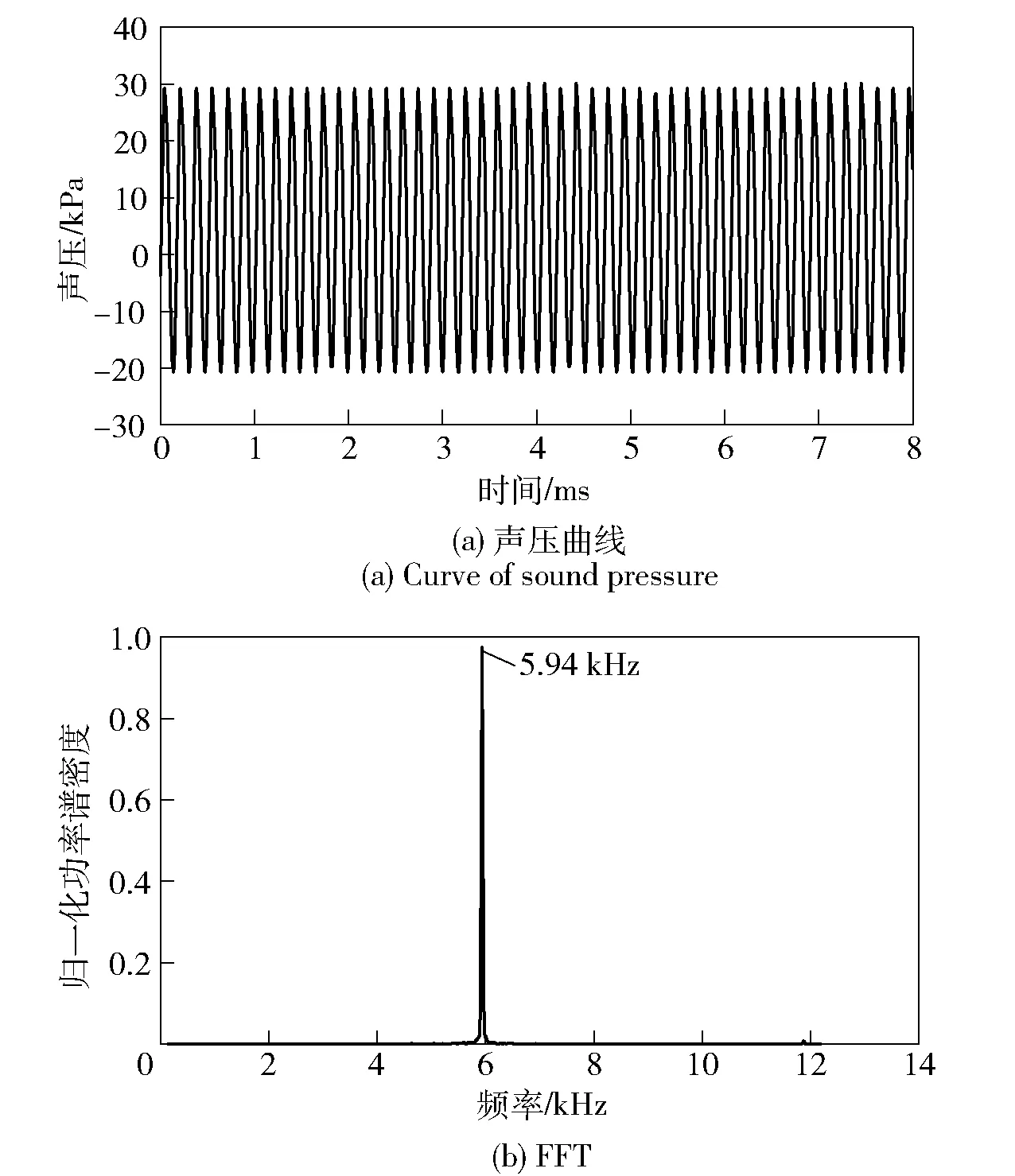
图4 L=10 mm及v=106 m/s时声压随时间的变化曲线Fig.4 Sound pressure vs. time for L=10 mm and v=106 m/s

图5 声压与流速的关系Fig.5 Relationship between sound pressure and airflow velocity

图6 频率与流速的关系Fig.6 Relationship between frequency and airflow velocity

3.2 间距影响

在分析间距对激振力的影响时，设计图1 的实验样机如下：L=7 mm，H=1 mm，X分别为2.0 mm、2.5 mm、3.0 mm、3.5 mm、4.0 mm. 激振力随时间的变化曲线以及对应的FFT如图7所示，声压曲线都呈正弦波形状，幅值和频率都比较稳定。实验结果如下：

图7 X=3 mm及v=74 m/s时声压随时间的变化曲线Fig.7 Sound pressure vs. time for X=3 mm and v=74 m/s

图8 声压与流速的关系Fig.8 Relationship between sound pressure and airflow velocity

图9 X=4.0 mm及v=53 m/s时声压曲线Fig.9 Sound pressure vs. time for X=4.0 mm and v=53 m/s

图10 X=2.0 mm及v=106 m/s时声压曲线Fig.10 Sound pressure vs. time for X=2.0 mm and v=106 m/s

图11 X=2.5 mm及v=127 m/s时声压曲线Fig.11 Sound pressure vs. time for X=2.5 mm and v=127 m/s

1)激振力幅值与流速的关系如图8所示。当流速较小(50～70 m/s)时，X越小其声压幅值越大；X越大其声压幅值越小或没有声振动产生，如图9所示，这是因为X越大时，射流振荡的损失较大，最终在共振腔内底部产生的声压幅值较小，从而导致激振力幅值较小或没有声振动产生。当流速较大(90～160 m/s)时，X越小其声压幅值越小或没有声振动产生，如图10和图11所示，这是因为X越小时，射流来不及形成振荡，使得在共振腔内底部产生的声压幅值较小，从而导致激振力幅值较小或没有声振动产生。

2)频率与流速的关系如图12所示。从图12中可知，激振力频率随入流的速度变大几乎呈线性趋势，且小间距激振机构的频率增大能力最强，增加幅度最大。结果表明，小间距对应的频率大，但间距越大，频率稳定性越好。

图12 频率与流速的关系Fig.12 Relationship between frequency and airflow velocity

根据以上分析可知，在较大流速情况下，为保证产生声波并获得稳定性好的高频振动频率，间距不能小于3.0 mm.

3.3 环隙影响

在分析环隙对压电换能器输出电压的影响时，设计图1的实验样机如下：L=8 mm，X=3 mm，H分别为0.5 mm、1.0 mm、1.5 mm. 激振力随时间的变化曲线以及对应的FFT如图13所示，声压曲线都呈正弦波形状，幅值和频率都比较稳定。实验结果如下：

图13 H=1.0 mm及v=85 m/s时声压随时间的变化曲线Fig.13 Sound pressure vs. time for H=1.0 mm and v=85 m/s

1)激振力幅值与流速的关系如图14所示。当流速较小(50～70 m/s)时环隙较小，其声压幅值变得越小或没有声振动产生，如图15所示。这是因为H较小(H=0.5 mm)时，射流振荡幅值较小，最终在共振腔内底部产生的声压幅值较小，从而导致激振力幅值较小或没有声振动产生。当流速较大(100～160 m/s)时，H过大则其声压幅值将变得越小或没有声振动产生，如图16所示。这是因为H较大(H=1.5 mm)时，射流不宜形成振荡，使得在共振腔内底部产生的声压幅值较小，从而导致激振力幅值较小或没有声振动产生。结果表明，H=1.0 mm时的激振机构，其振幅值始终处于最大，存在振幅随入流速度线性变大的临界环隙值。

图14 声压与流速的关系Fig.14 Relationship between sound pressure and airflow velocity

图15 H=0.5 mm及v=53 m/s时声压曲线Fig.15 Sound pressure vs. time for H=0.5 mm and v=53 m/s

图16 H=1.5 mm及v=116 m/s时声压曲线Fig.16 Sound pressure vs. time for H=1.5 mm and v=116 m/s

2)激振力频率与流速的关系如图17所示。从图17中可知，环隙越大，频率越高，且频率随入流速度近似线性增大，高入流速度时，频率偏差值都在500 Hz左右，表明其频率的稳定性较好。

图17 频率与流速的关系Fig.17 Relationship between frequency and airflow velocity

根据以上分析可知，为了获得高振幅、高频振动信号，需将环隙值控制在合理的范围内。

4 结论

本文通过模拟吹风实验研究，对影响激振力幅值和频率的结构参数进行了分析。由实验结果得出以下结论：

1) 不同共振腔长度对应的激振力幅值与入流速度近似呈现线性增大趋势，且长度越大其斜率越小，反之亦然；间距和环隙对激振力幅值的影响较复杂，过大或过小都会使得激振力幅值较小甚至没有声压波形产生。

2) 共振腔长度是影响激振力频率的主要因素，频率随长度的增大而变小，呈反比关系；间距和环隙对频率的影响较小。

因此，对于高速气流，短共振腔可以获得较大幅值的高频稳定激振力；另外，需合理控制间距和环隙，使得激振力幅值较大。由此获得的结构敏感参数值可作为工程设计的依据。

References)

[1] 李映平．引信压电发电机原理及试验研究[D]．南京：南京理工大学，2006．

LI Ying-ping. The principle of fuze piezoelectric power supply and experimental investigations [D]．Nanjing: Nanjing University of Science and Technology，2006．(in Chinese)

[2] 黎晖，高敏，王广龙．引信用压电式射流发电机的原理与研究[J]．电源技术，2009，33(12)：1120-1122．

LI Hui，GAO Min，WANG Guang-long．Principle and analysis of piezoelectric fluidic generator for fuze[J]．Power Technology，2009，33(12)：1120-1122．(in Chinese)

[3] 雷军命．引信气流谐振压电发电机[J]．探测与控制学报，2009，31(1)：23-26．

LEI Jun-ming．An air-driven fluidic resonance piezoelectric generator for fuze [J]．Journal of Detection & Control，2009，31(1)：23-26．(in Chinese)

[4] 徐伟，王炅，陆静．引信用MEMS气流谐振压电发电机[J]．探测与控制学报，2011，33(1)：9-13．

XU Wei，WANG Jiong，LU Jing．MEMS air-driven fluidic resonance piezoelectric generator for fuze [J]．Journal of Detection & Control，2011，33(1)：9-13．(in Chinese)

[5] 何鹏. 引信新型弹载发电机气流控制进气口内流场数值模拟[D]. 南京: 南京理工大学, 2012.

HE Peng. Numerical simulation of airflow control inlet internal flow field of fuze on-boarded generator [D]. Nanjing: Nanjing

University of Science and Technology, 2012. (in Chinese)

[6] 邹华杰，陈荷娟，梁医．引信振动压电发电机气流致声振源特性研究[J]．兵工学报，2015，36(4)：610-618．

ZOU Hua-jie，CHEN He-juan，LIANG Yi．Study of airflow-induced acoustic characterization of fuze vibration piezoelectric generator [J]． Acta Armamentarii，2015,36(4)：610-618． (in Chinese)

[7] Li F．Numerical analysis of vortex shedding behavior of piezoelectric microgenerator from dynamic airflow induced vibration[J]．Advanced Materials Research，2013，694：1595-1601．

[8] 邹华杰，陈荷娟，赖长缨，等．微环音气流压电发电机声管固定方法[J]．探测与控制学报，2014，36(3)：25-30.

ZOU Hua-jie，CHEN He-juan, LAI Chang-ying, et al．Fixation methods of sound tube of micro ringtone airflow piezoelectric generator[J]．Journal of Detection & Control，2014，36(3)：25-30．(in Chinese)

[9] Priya S， InmanD J．Energy harvesting technologies [M]．NY, US: Springer，2009：26-27．

[10] Zou H J，Chen H J，Zhu X G. Piezoelectric energy harvesting from vibration induced by jet-resonator system [J]. Mechatronics, 2015，26(2): 29-35.

[11] 马大猷．现代声学理论基础[M]．北京：科学出版社，2004：296-306．

MA Da-you．Modern acoustic theory foundation[M]．Beijing：Science Press，2004: 296-306．(in Chinese)

AnalysisofStructureParametersofAirflow-inducedVibrationPiezoelectricGeneratorforFuze

ZOU Hua-jie1,2, ZHANG Jiang-hua1, CHEN He-juan2, WANG Ze-ping1
(1.College of Mechanical Engineering, Changzhou Vocational Institute of Mechatronic Technology, Changzhou 213164，Jiangsu，China；2.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094，Jiangsu，China)

In order to meet the requirements of airflow-induced vibration of small piezoelectric generator for fuze, and solve the critical issue of stable excitation force, the key is to effectively control the sensitive parameters of generator structure. The influence of related structural parameters of airflow-induced excitation device on excitation force is analyzed through simulating flow test. The test result shows that the amplitudes of excitation force corresponding to different resonator lengths increase approximately linearly with the airflow velocity, and the longer the length of resonator is, the smaller the slope is, and vice versa. The space between nozzle and resonator and the ring gaps have the complex effects on the amplitude of excitation force , and too big or too small gap would make the amplitude smaller or even no waveform formed. The length of resonator is the main factor impacting on the frequency of excitation force, and the frequency decreases with the increase in the resonator length, presenting an inverse relationship. The space between nozzle and resonator and the ring gaps have less effects on the frequency of excitation force. Therefore, for high airflow velocity, the stable excitation force with high amplitude and frequency can be obtained by short resonator. In addition, reasonable space and ring gaps are also important for ensuring bigger amplitude of excitation force. The resulting sensitive parameter values of sound excitation device can be used as references for engineering design.

ordnance science and technology； fuze; airflow-induced sound; piezoelectric generator; excitation force

2017-03-02

国家自然科学基金项目(51377084)； 江苏省自然科学基金青年基金项目(BK20160296)

邹华杰(1988—)， 男， 讲师， 博士。 E-mail: zhj88000@163.com

TJ430.3+8

A

1000-1093(2017)10-2055-07

10.3969/j.issn.1000-1093.2017.10.023