超声椭圆振动车削三维形貌形成研究

张国华， 李咚咚， 李茂伟， 张德远

(1.北京卫星制造厂， 北京 100094；2.北京航空航天大学 机械工程及自动化学院， 北京 100191)

超声椭圆振动车削三维形貌形成研究

张国华1， 李咚咚1， 李茂伟1， 张德远2

(1.北京卫星制造厂， 北京 100094；2.北京航空航天大学 机械工程及自动化学院， 北京 100191)

为研究椭圆振动车削表面三维几何形貌形成规律及影响因素，采用金属切削理论对椭圆振动切削过程和三维切削模型进行了分析。研究结果发现：切削过程中相邻两转之间不同的相位差特征值对最终表面形貌有着重要的影响；通过已有的试验结果表明，相位差特征值分别为0和0.5时所形成的表面形貌截然不同，与理论分析结果相吻合。

机械制造工艺与设备; 超声椭圆振动; 表面形貌; 精密加工

0 引言

超声椭圆振动车削是一种新型加工方法[1]，具有降低切削力[2-4]、提高零件系统的稳定性[5-7]、提高表面质量的优势，特别是在航空航天、兵器工业和难加工材料精密及超精密等加工领域内发挥了重要的作用。

然而，从目前绝大部分的研究成果和文献可以看出，针对超声椭圆振动车削表面形貌的研究还比较少，现有的研究主要基于实验手段来验证表面质量提高，或是基于振动往复熨压的切削特性来分析研究表面成因[8-12]。对于椭圆振动车削表面微观几何形貌形成的研究领域几乎处于空白，这束缚了超声椭圆振动车削在精密及超精密等加工领域内的进一步推广应用。

本文针对超声椭圆振动精密加工过程中表面微观几何形貌形成进行了详细研究，通过已有的实验结果进行了验证，验证了分析的准确性。

1 椭圆振动车削三维形貌形成机理

1.1 表面几何形貌理论公式的推导

对相位差不存在时椭圆振动车削表面形成机理前人已进行了分析，但是对相位差存在时表面几何形貌形成机理还没有系统的研究，故本文对表面几何形貌形成机理进行全面的研究。

选择带圆弧的刀具，取工件一个区域进行分析。普通车削加工时，圆弧刀具在已加工表面形成了图1所示的进给刀纹纹路。如果进给量fv满足fv≤2Rεsink′r，k′r为刀具的副偏角，则进给刀纹最大高度由几何关系[13]可知：

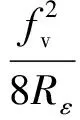
(1)

式中：Rε为刀尖圆弧半径。

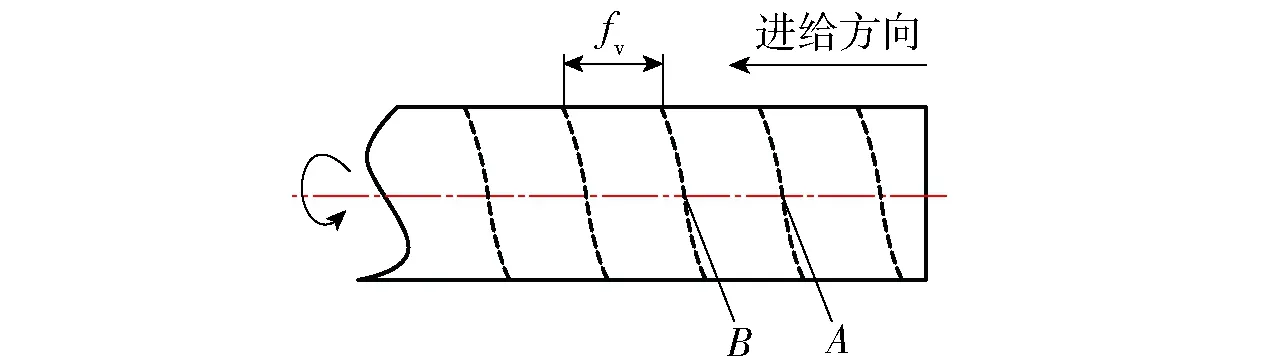
图1 工件车削位置Fig.1 Cutting position of workpiece

由(1)式可知，进给刀纹的几何高度仅与fv、Rε有关。精密加工时，由于两个参数都是在同一数量级，因此fv对H的影响相比Rε的影响更大一些。

椭圆振动车削过程中，刀具同时存在两个方向相互垂直振动：其中一个振动方向平行于切削速度，使得刀具产生周期性的分离运动；另一个振动方向垂直于切削速度，在切削方向上形成一系列具有一定高度的振纹，进给方向上的刀纹和切削方向上的振纹近似于相互垂直。在切削的过程中两者相互影响，彼此有一定的削弱作用，最终形成了椭圆振动车削所特有的表面形貌，其中垂直于切削速度的振动对已加工面的表面几何高度有着重要的影响。

超声振动对系统颤振有着极强的抑制作用，故不考虑系统颤振的影响，从几何角度来分析表面形貌的形成规律。如图2所示，取圆弧刀刃与进给刀纹相切的一点G进行分析，任意时刻刀具椭圆振动控制方程[12]如(2)式所示：

(2)

式中：AXmax为X坐标进给方向最大振幅值；AX为X坐标进给方向任意振幅值；AYmax为Y坐标进给方向最大振幅值；AY为Y坐标进给方向任意振幅值；w为超声椭圆振动加工频率；θ为刀具振动相位角。

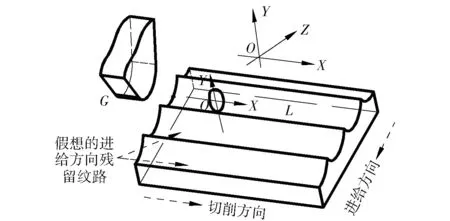
图2 刀具- 工件位置关系Fig.2 Position of cutting tool and workpiece

刀具由椭圆轨迹不同振动点开始切入时，由于刀具振动形式不同，切入工件后所形成的表面形貌也有所不同。工件转动一圈，刀具从A点到B点的切削行程为L，定义为刀具的一次切削行程，如图1所示。图2及图3中的工件为沿周向的展开图，对比之前的研究方法，引入频率行程速度系数KL：

KL= 2wL/v=m+n,

(3)

式中：v为刀具本身切削速度(不含振动速度)；m为整数；n为小数或0.

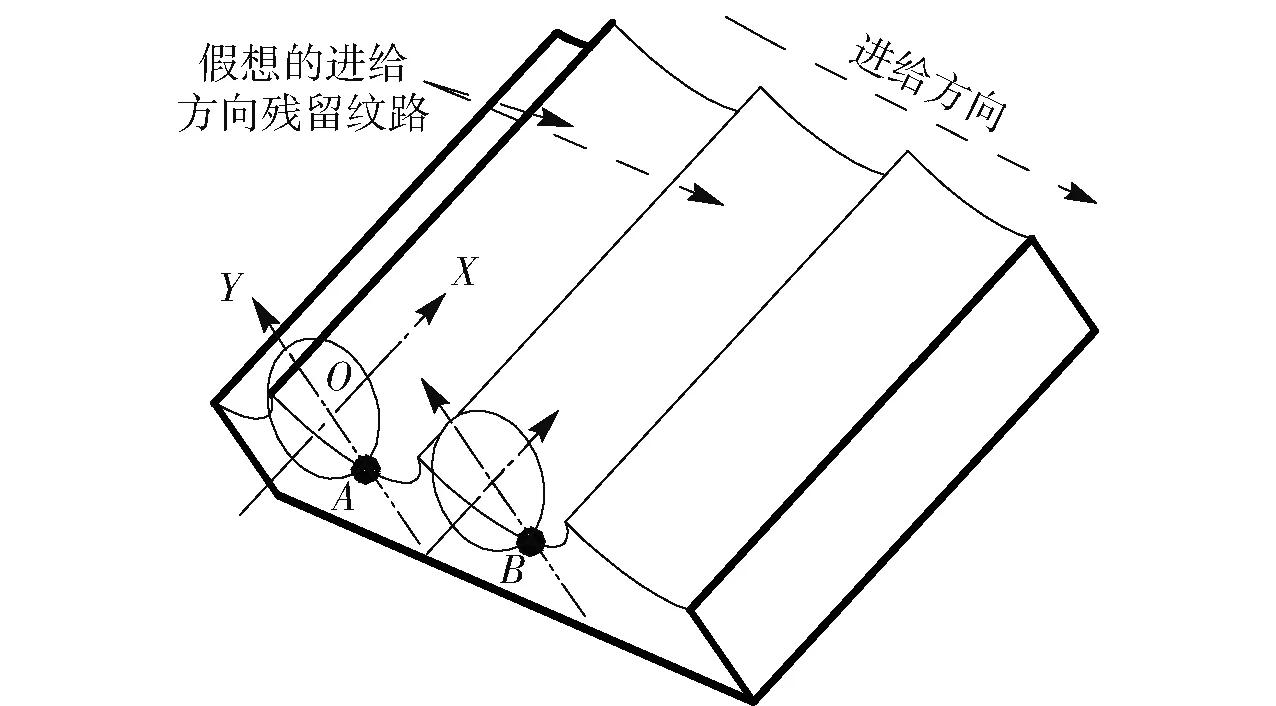
图3 刀具任意振动状态切入工件Fig.3 Cutting tool cutting into workpiece in any vibrational state

规定刀具一个完整的振动形态是走完一个完整的椭圆弧长s，椭圆轨迹走向沿进给方向看从起始点A点顺时针再回到A点，如图3所示。将n定义为相位差特征值，表达公式为

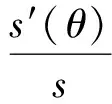
(4)

式中：s′(θ)是从起始点A点顺时针振动到任一点的弧长。

对图1、图3进行分析，假如在B点完成车削时，n=0，则KL只有整数部分m，那么以A点瞬时振动形态作为参考，可知在切削行程L距离内刀具运动到B点时完成了m个的完整椭圆轨迹，即在A点与B点刀具的瞬时振动形态完全一致，由(2)式可知，刀具椭圆振动控制方程完全一致，故相邻连转不存在相位差；如果在B点完成车削时，n≠0，则KL由整数部分m和小数部分n构成的，那么以A点瞬时振动形态作为参考，可知在切削行程L距离内刀具运动到B点时完成了m个完整椭圆轨迹和n个椭圆轨迹，即A点与B点刀具的瞬时振动形态不一致，由(2)式可知，刀具椭圆振动控制方程不一致，必然造成A点的相位θ值与B点的相位θ值不等，故相邻连转存在相位差，因此其中n可以表征反映出相邻两转之间的相位差。

1.2 相位差不存在时几何形貌形成分析

刀具起振点位于椭圆轨迹上A点时，刀具开始切入工件，A点轨迹参数为

(5)

切完第1刀后，第2刀车削时，刀具由椭圆轨迹上B点开始切入工件，A点与B点刀具的瞬时振动形态完全一致，如(5)式所示，即相位差特征值n=0.A点与B点不存在相位差，在平行于进给方向的任意切平面的位置上，相邻两刀的椭圆最低点A′点和B′点必然在同一水平位置，如图4所示。已加工表面的形貌如图5(a)所示，其俯视图投影后得到图5(b)。

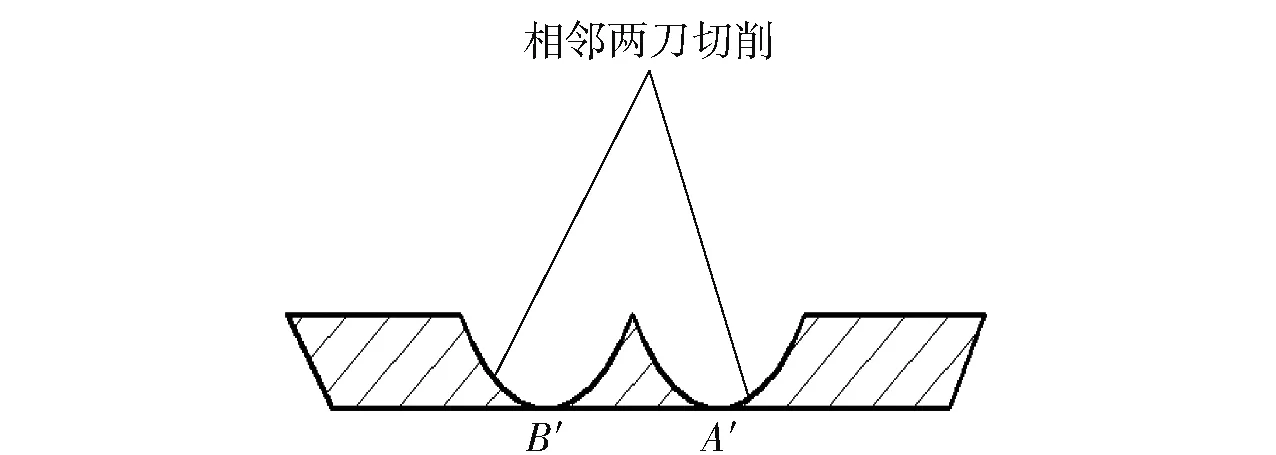
图4 在椭圆最低点切削后截面形状Fig.4 Shape at the lowest elliptical point

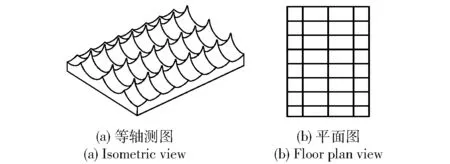
图5 椭圆振动车削三维形貌(n=0)Fig.5 3-D micro-surface shapes in ultrasonic elliptical vibration cutting(n=0)

该类型的表面形成机理基于工件相邻两刀车削时刀具以相同振动状态切入，李勋等[14]对此已经作了相应的研究，并对成型机理及影响因素进行了详细分析，表面几何高度值为车削形成的最高点至最低点的距离：H=RCC+REVC+R′CC，其中RCC为普通切削表面几何高度，REVC为超声切削表面几何高度，R′CC为普通切削与超声切削相互削弱的表面几何高度值。

1.3 相位差存在时几何形貌形成分析

但是大多数椭圆振动车削过程中，不可避免地存在相位差，这使得表面几何形貌形成过程更加复杂。假定第1刀车削时，刀具由椭圆轨迹上任意形态A点车削，第2刀车削时，刀具由椭圆轨迹上任意形态B点开始切入工件，即相位差特征值n≠0，如图3所示。

这种车削状态下形成如图6所示的三维表面形貌，由刀具Y方向振动和进给量的影响而形成的表面形貌几何高度H满足：H=RCC+REVC，图6中给出了第1刀沿椭圆1车削分别形成波谷1和波峰3，第2刀沿椭圆2车削分别形成波谷2、波峰1和波峰2. 形成过程可以描述如下：刀具沿椭圆1切入后，受到垂直于切削速度方向的Y方向振动影响，形成一系列的振纹高点；刀具沿椭圆2切入后，受到相位差及进给量的影响，相邻两刀的刀具轨迹形成重叠，第2刀切削就会对第1刀切削所形成振纹高点的重叠区域进行重复切削，该高点被切去一部分，从而振纹高度有所降低。

图6 椭圆振动车削三维形貌(n≠0)Fig.6 3-D micro-surface shape in ultrasonic elliptical vibration cutting(n≠0)

如果相位差特征值n由0逐渐增大时，波谷1就会在波峰1与波峰2之间变动游走，很明显地发现波谷1与波谷2重合时，波峰3与波峰1重合，此时重复切削量最少，表面形貌几何高度H最大，振动形态相同时，相位差特征值n为0；随着相位差特征值n逐渐增大到0.5时，表面形貌几何高度H值逐渐降低，当波谷1与波峰2重合，波峰3与波谷2重合，此时重复切削量最多，H值达到最小；随着相位差特征值n继续增大到1时，表面形貌几何高度H值又开始逐渐增大，当波峰3与波峰2重合，此时重复切削量最少，表面形貌几何高度H最大，此时相位差特征值n=1. 据此分析，相位差特征值n=0时，表面形貌几何高度H值最大；相位差特征值n=0.5时，表面形貌几何高度H值最小；相位差特征值n为其他值时，表面形貌几何高度H值介于这两者之间。

相位差特征值n=0.5时刀具位于两个点的相对位置如图7(a)所示，由椭圆轨迹上A点开始切入工件，A点轨迹参数为

(6)

切完第1刀后，第2刀车削时，刀具由椭圆轨迹上B点开始切入工件，B点参数表达同(5)式。

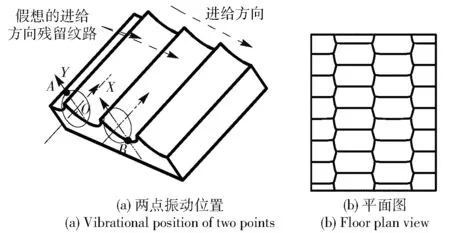
图7 椭圆振动车削三维表面形貌(n=0.5)Fig.7 3-D micro-surface shapes in ultrasonic elliptical vibration cutting(n=0.5)

图7(a)所处的加工位置开始加工，所形成的最终表面形貌类似图6，将图6在俯视图方向投影得到如图7(b)所示图形。

此外，不同的相位差特征值n所得到最终三维形貌基本类似图6所示，只是第1刀波峰和第2刀所形成的波谷相对位置不同，相对位置沿着X方向发生了错动。针对普通状况，列出了4种不同的相位差特征值n车削后所形成的表面形貌，俯视平面图如图8所示。

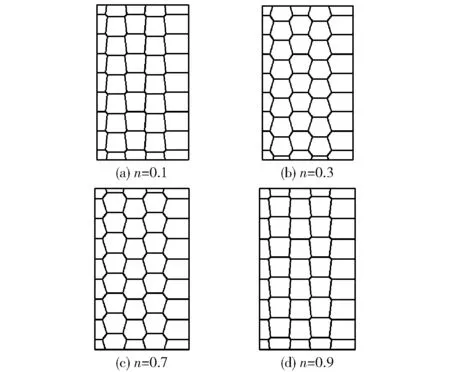
图8 椭圆振动车削三维表面形貌Fig.8 3-D micro-surface shapes in ultrasonic elliptical vibration cutting

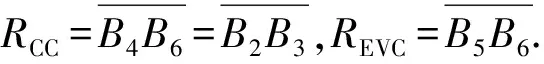
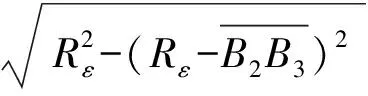
(7)

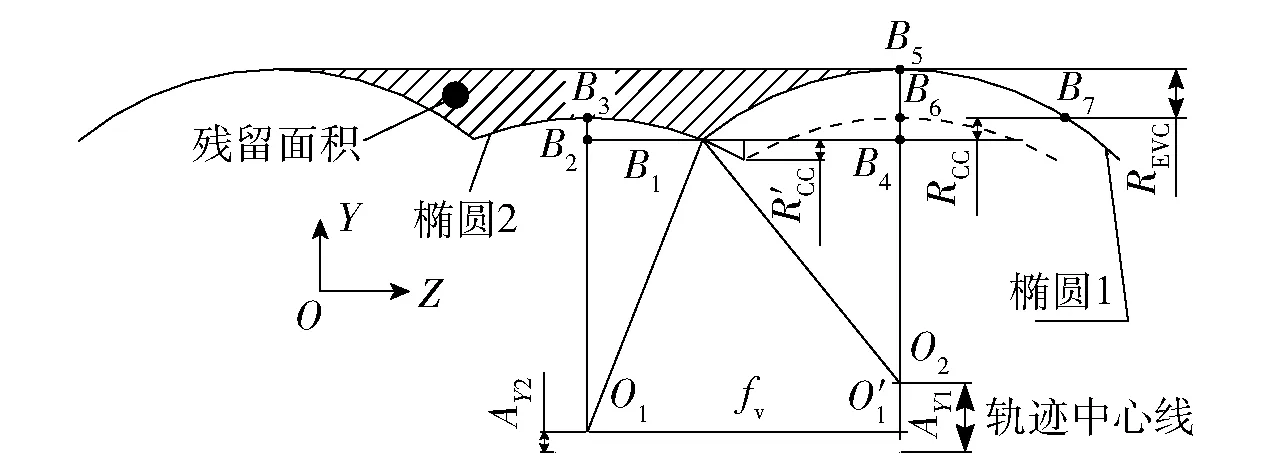
图9 相邻两转刀具轨迹几何关系Fig.9 Geometrical relationship of cutting tool between two adjacent turns

将上述几何关系代入(5)式，整理可得:

(8)

当振动频率w=0时，REVC=0，有H=RCC，(8)式退化为

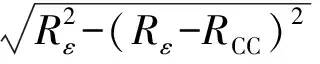
(9)

(9)式为普通车削表面形貌几何高度公式。故(8)式将超声振动车削与普通车削所形成的表面形貌几何高度理论公式统一起来。椭圆振动车削刀具运动轨迹控制方程式如下：

(10)

分析图10所示轨迹，为方便研究刀具在一个周期内的车削过程，不妨令刀具切入点位于Ps点，刀具位于P0点时，刀具Y负方向位于最大振幅位置，X正方向的振动速度达到大。此后X方向的振动速度开始逐渐减小，在Y方向的振幅为0时，振动速度减小至0. 此后刀具X方向振动速度开始增大，振动方向发生改变与工件运动的方向一致。当刀具运动到临界点P1点时，刀具X方向的速度达到临界速度，刀具开始与工件分离，刀具在下一次切入之前一直保持空切状态。此后刀具X方向的振动速度继续增大，当位于Y正方向最大振幅位置时，X负方向的振动速度达到最大。此后振动速度开始逐渐减小，在Y方向的振幅为0时，X负方向振动速度减小至0. 此后刀具X方向振动速度开始增大，振动方向发生改变与工件运动方向相反。由于对称性，刀具运动到第2个临界点P2点时，刀具X正方向的速度达到临界速度。此后刀具X正方向的振动速度继续增大，刀具运动到P3点时，刀具再次切入工件。至此刀具完成一个周期的车削，其中分离点和切入点如图10所示。取P0点刀具轨迹时间和位置作相对起点，则此刻P1点、P2点、P3点所对应的时间及位置分别为t1、t2、t3及X1、X2、X3，图10中P1点和P2点满足对称性，则有

(11)

图10 刀具切入与分离过程Fig.10 Cutting-in of cutting tool and its separation from workpiece

两个分离点速度方向满足以下条件：

(12)

P1点和P2点满足对称性：

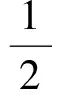
(13)

联立(11)式、(12)式、(13)式，可求H.

2 椭圆振动切削参数对表面形貌的影响

2.1 频率行程速度系数的影响

利用数值解析法求KL与H的关系，如图11所示。

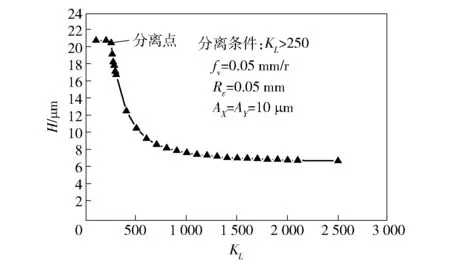
图11 频率行程速度系数- 表面几何高度曲线Fig.11 Relation between frequency travel speed coefficient and surface geometric height

图11中分离点左侧区域为分离区，右侧区域为不分离区。分析图11，在分离区：其他参数确定后，表面形貌几何高度H值随着KL的增大而逐渐降低，并且降低的趋势逐渐变缓，最终接近某一个数值并不会一直减小至0. 因此在满足车削加工的各项指标时，可以采用尽可能大的频率行程速度系数KL. 但是随着KL值增大到一定范围后，试图通过继续增加KL值来改善表面加工质量，效果会变的很微弱。随着KL值的增大，形成的表面形貌几何H值越来越低，这符合图11中的趋势。

2.2 切削参数的影响

为了进一步研究其他切削参数对表面形貌几何高度的影响，根据(8)式，作出了进给量—表面几何高度关系曲线、Y方向振幅—表面几何高度关系曲线、刀尖圆弧半径—表面几何高度关系曲线，如图12、图13及图14所示。

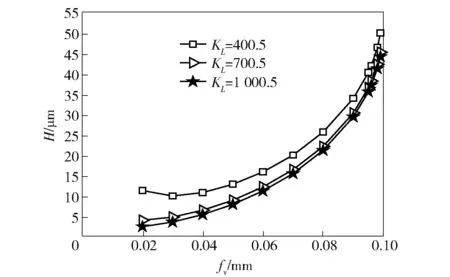
图12 进给量—表面几何高度曲线Fig.12 Relation between feed and surface geometric height

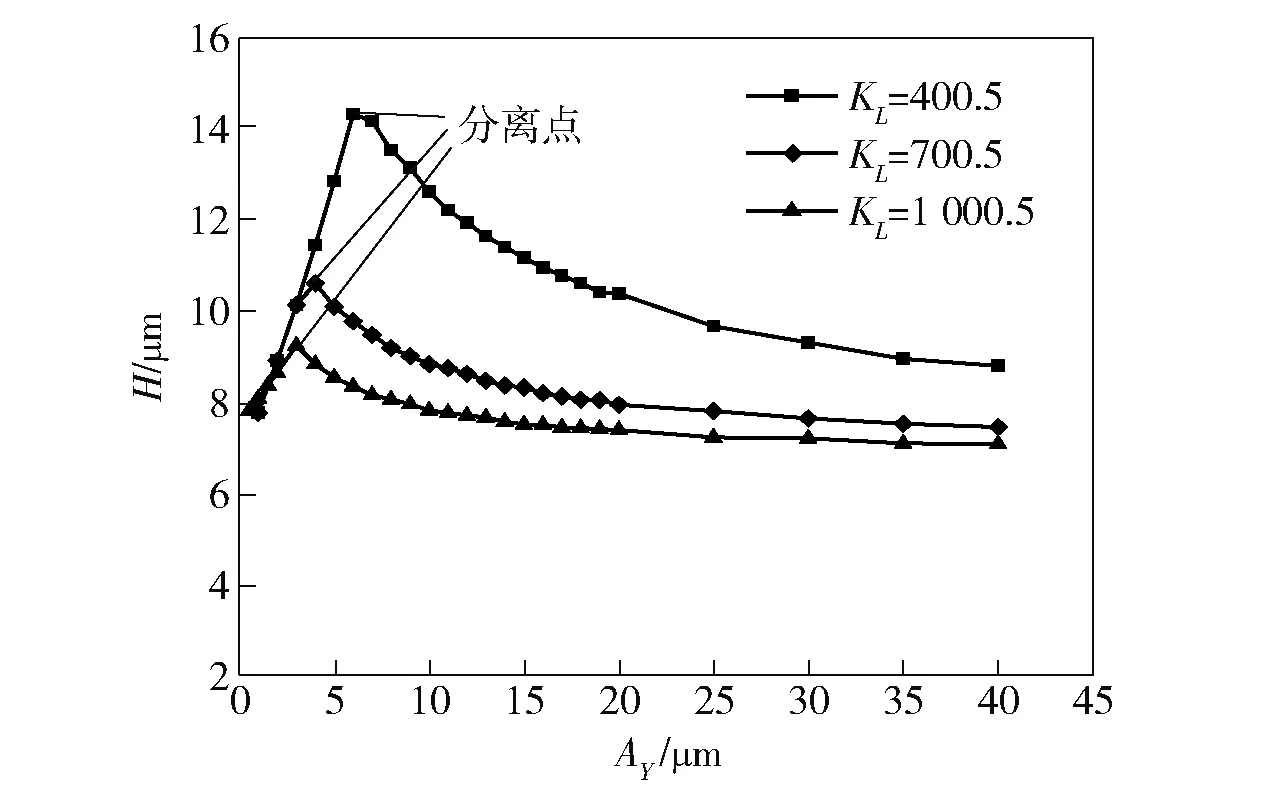
图13 Y方向振幅—表面几何高度曲线Fig.13 Relation between Y amplitude and surface geometric height

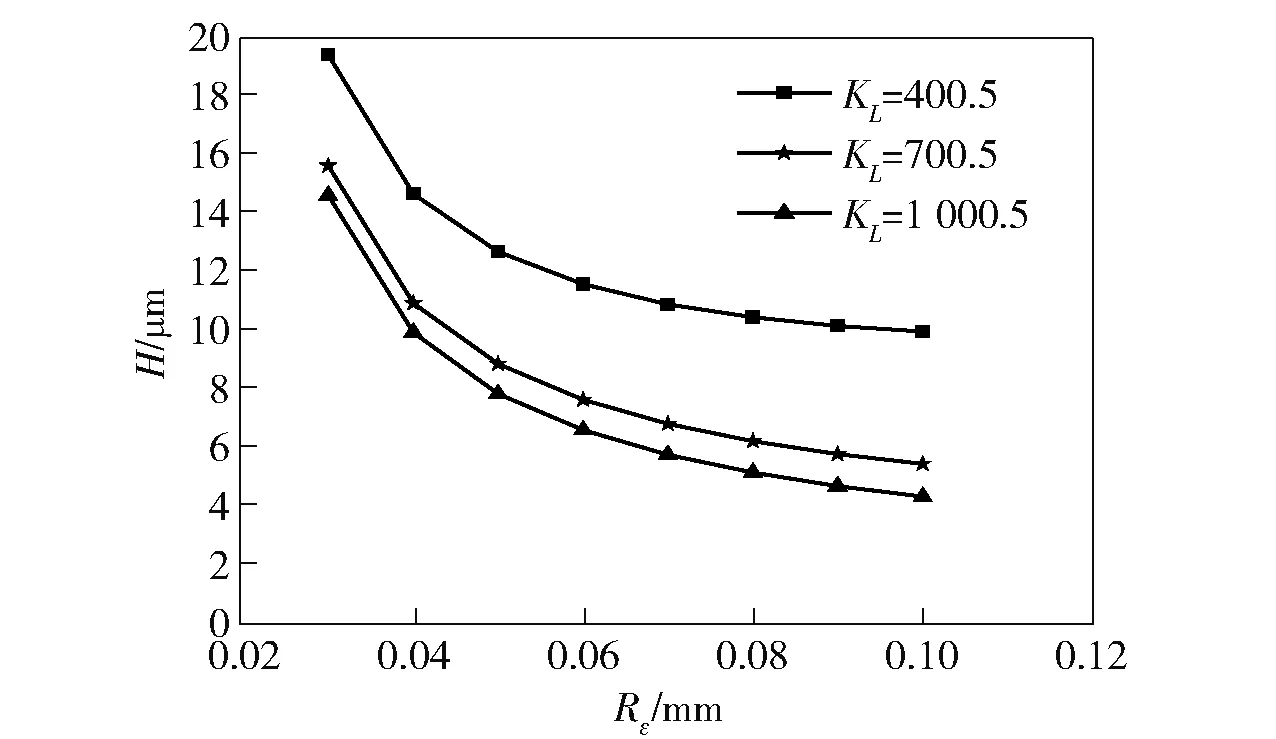
图14 刀尖圆弧半径—表面几何高度曲线Fig.14 Relation between cutting tool’s circular arc radius and surface geometric height

从图12可以看出：频率行程速度系数KL确定后，随着进给量fv值的增加，表面形貌几何高度H逐渐增大，并且当fv接近2Rε时，H值逐渐接近于刀尖圆弧半径Rε. 从图12中还可以知道，KL值逐渐增大可以在抑制由于进给量fv值增加而造成的已加工表面量恶化。但是频率行程速度系数KL增到一定范围后，这种抑制作用就变得不明显了。同时也可看出进给量fv值对H的影响要大于频率行程速度系数KL值。

图13中分离点左侧区域为相应参数下的分离区，右侧区域为不分离区。从图13可以看出：在分离区，频率行程速度系数KL值确定后，随着Y方向振幅AY的增加，表面形貌几何高度H逐渐减小；当AY值增大到几十微米后，H值逐渐接近某一固定数值。事实上对于超声振动车削，由于受到现有材料及换能器设计原理的限制，刀具单边振幅很难达到很大，因此很难作到已加工表面的H值接近图13中比较理想的状态。对比KL=400.5、KL=700.5和KL=1 000.5这3条曲线，可以看出，KL值越大，H值对Y方向振幅变化越不敏感。KL值比较大的时候，试图通过调整Y方向振幅大小来改善表面形貌，效果并不是很明显。在不分离切削区，Y方向振幅增大，表面形貌几何高度H随之增大。因此当刀具处于不分离区进行切削时，为获得比较好的表面形貌，Y方向振幅应尽可能的小。

从图14可以看出，表面形貌几何高度H随着刀尖圆弧半径增大而减小，频率行程速度系数KL越大，刀尖圆弧半径的这种影响也就越弱。

3 椭圆振动车削试验验证

图15 双弯复合椭圆振动系统原理图Fig.15 Double bending composite elliptical vibration system

为了更清楚地验证第2节相位差对表面三维形貌影响的准确性，以李勋等[14]所做的车削试验结果来验证前面分析的正确性，车削试验系统为双弯椭圆振动系统及试验系统，振动原理如图15、图16所示。

图16 车削试验系统图Fig.16 Vibration cutting test system

椭圆振动车削过程中主要的切削条件及参数如表1所示。

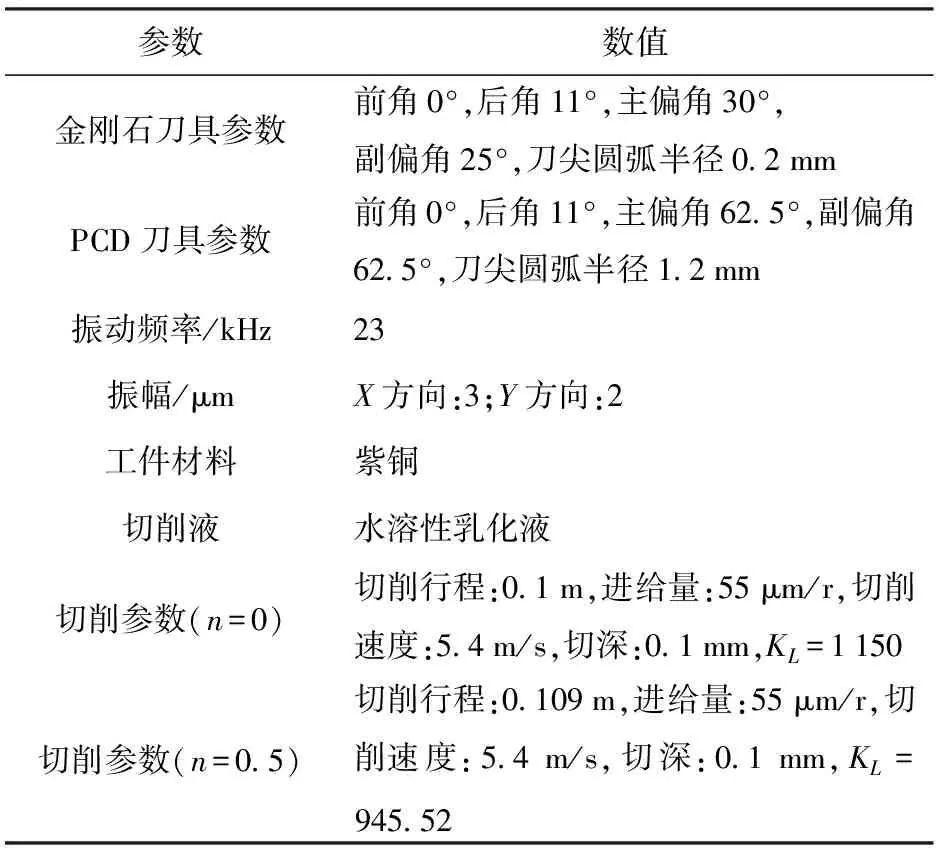
表1 超声椭圆振动车削试验条件

依据李勋等[14]试验所得到的表面形貌照片如图17所示。在频率行程速度系数KL中的相位差特征值n=0时，对比理论分析所得到图5(a)与试验所得到的图17(a)，可以发现两者的表面形貌一致性非常好；相位差特征值n=0.5时，对比理论分析图5(b)与试验所得到的图17(b)，可以发现两者的表面形貌一致性非常好。

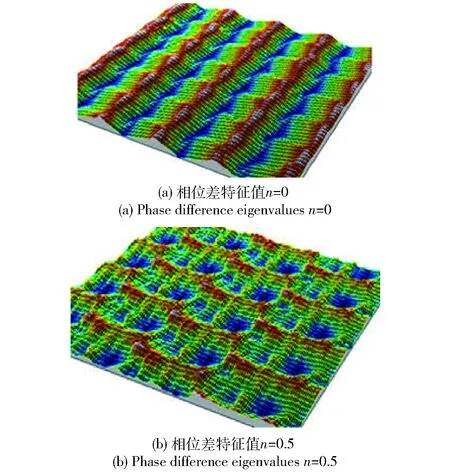
图17 不同频率行程速度系数的微观几何形貌Fig.17 Micro-surface shapes at different frequency travel speeds

通过相位差特征值n取两种不同值的对比分析，验证了第2节分析的频率行程速度系数KL对表面几何形貌影响的正确性，也说明了在实际加工过程中相位差特征值对微观表面几何形貌的形成有着重要的影响。

4 结论

1)通过理论分析，推导出了超声椭圆振动表面形貌理论公式，将普通车削与超声振动车削理论公式统一起来；椭圆振动车削时，切削表面几何形貌是由进给刀纹和Y方向振动产生的振纹彼此削弱、共同作用而形成的。

2)最终的表面形貌几何高度H值是由频率行程速度系数KL、进给量、Y方向振幅和刀尖圆弧半径共同决定的，每个参数对H值的影响各有不同。

3)通过试验验证了相位差特征值n是否为0对表面几何形貌有着重要的影响，两者呈现出截然不同的表面形貌。

References)

[1] 隈部淳一郎. 精密加工- 振动切削基础与应用[M]. 韩一昆，译. 北京: 机械工业出版社, 1985.

Kumabe J．Fundamentals and application of vibration cutting[M]．HAN Yi-kun，translated．Beijing：China Machine Press，1985．(in Chinese)

[2] Ma C X，Shamoto E，Moriwaki T．Study on the thrust cutting force in ultrasonic elliptical vibration cutting [J].Materials Science Forum, 2004: 396-400, 467-470．

[3] 张德远, 张成茂. 飞机交点孔超声椭圆振动精密加工技术[J]. 中国机械工程, 2012, 23(1):39-41．

ZHANG De-yuan, ZHANG Cheng-mao．Ultrasonic elliptical vibration precision machining for aircraft intersection holes [J]．China Mechanical Engineering, 2012, 23(1):39-41．(in Chinese)

[4] Zhou X Q, Zuo C M, Liu Q, et al. Surface generation of freeform surfaces in diamond turning by applying double-frequency elliptical vibration cutting[J]. International Journal of Machine Tools & Manufacture, 2016, 104:45-57.

[5] Zhang J, Suzuki N, Wang Y, et al. Ultra-precision nano-structure fabrication by amplitude control sculpturing method in elliptical vibration cutting[J]. Precision Engineering, 2015, 39:86-99．

[6] Kim G D，Loh B G．An ultrasonic elliptical vibration cutting device for micro V-groove machining：kinematical analysis and micro V-groove machining characteristics[J]．Journal of Materials Processing Technology，2007, 190(1):181-188．

[7] 马春翔，社本英二，森肋俊道，等．超声波椭圆振动切削提高加工系统稳定性的研究[J]．兵工学报，2004，25(6)：752-756．

MA Chun-xiang，Shamoto E，Moriwaki T，et a1．Study on the improvement of machining system stability by applying ultrasonic elliptical vibration cutting[J]．Acta Armamentarii，2004，25(6)：752-756．(in Chinese)

[8] Jung H, Hayasaka T, Shamoto E. Mechanism and suppression of frictional chatter in high-efficiency elliptical vibration cutting[J]. CIRP Annals-Manufacturing Technology, 2016, 65(1):369-372.

[9] Lin J, Han J, Zhou X, et al. Study on predictive model of cutting force and geometry parameters for oblique elliptical vibration cutting[J]. International Journal of Mechanical Sciences, 2016, 117:43-52．

[10] Nath C，Rahman M，Neo K S．A study on the effect of tool nose radius in ultrasonic elliptical vibration cutting of tungsten carbide [J]．Journal of Materials Processing Technology，2009，209(17)：5830-5836．

[11] Kurniawan R, Kiswanto G, Ko T J. Micro-dimple pattern process and orthogonal cutting force analysis of elliptical vibration texturing[J]. International Journal of Machine Tools & Manufacture, 2016, 106:127-140.

[12] 张成茂，张德远．导套式椭圆超声镗削模拟实验研究[J]．兵工学报，2013，34(4)：465-470．

ZHANG Cheng-mao, ZHANG De-yuan．Simulation experiment study on elliptical ultrasonic vibration boring of leading bushing [J]．Acta Armamentarii，2013，34(4)：465-470．(in Chinese)

[13] 陈日曜. 金属切削原理[M]. 第2版.北京: 机械工业出版社，2012.

CHEN Ri-yao．Metal-cutting principie [M]．2nd ed. Beijing：China Machine Press，2012．(in Chinese)

[14] 李勋, 张德远. 超声椭圆振动切削表面形貌形成机理的研究[J]. 中国机械工程, 2009, 2(7): 807-811.

LI Xun，ZHANG De-yuan．Research on micro-surface formation mechanism of ultrasonic elliptical vibration cutting [J]．China Mechanical Engineering，2009, 2(7): 807-811．(in Chinese)

ResearchonFormationof3-DMicro-surfaceinUltrasonicEllipticalVibrationCutting

ZHANG Guo-hua1， LI Dong-dong1， LI Mao-wei1， ZHANG De-yuan2
(1.Beijing Satellite Manufacturing Factory，Beijing 100094, China；2.School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China)

In order to find the influence factors and the influence law of the 3-D micro-surface formation of ultrasonic elliptical vibration cutting, the elliptical vibration cutting process and 3-D cutting model are analyzed based on the metal cutting theory. The results show that the different phase difference eigenvalue between two adjacent turns in vibration cutting process has an important influence on the final surface geometry. The existing cutting test results show that the final surface shapes with the eigenvalues of 0 and 0.5 are very different, and the results agree with the theoretically analyzed results.

manufacturing technology and equipment; ultrasonic elliptical vibration; surface morphology; precision machining

2017-04-06

张国华(1985—)，男，工程师。E-mail：zgh650@163.com

张德远(1963—)，男，教授，博士生导师。E-mail：zhangdy@buaa.edu.cn

TG506.5

A

1000-1093(2017)10-2002-08

10.3969/j.issn.1000-1093.2017.10.017