基于落点的弹道导弹需要速度求解方法*

范金龙,刘新学,武 健,刘庆国

(火箭军工程大学,西安 710025)

基于落点的弹道导弹需要速度求解方法*

范金龙,刘新学,武 健,刘庆国

(火箭军工程大学,西安 710025)

为了提高需要速度的求解精度,解决当前飞行状态和目标位置不定情况下需要速度的求解问题,文中提出了一种基于落点的需要速度求解方法。在惯性坐标系下,建立了需要速度的求解模型,对目标点与弹道导弹绝对弹道面之间的纵横向偏差进行修正,计算导弹当前飞行状态下的需要速度。仿真结果证明,该方法可有效求解空中某飞行状态下导弹的需要速度,精度较高,打击目标可以适当变换。

弹道导弹;落点;绝对弹道面;需要速度;变换目标

0 引言

闭路制导方法的基本思想[1]是:导弹发射前,根据发射点和目标点的位置计算虚拟目标,在制导过程中,首先,根据导弹的真位置矢r、真速度矢v和虚拟目标m′,按照椭圆弹道理论求解导弹的需要速度vR;然后,根据vR和当前导弹飞行的真速度矢v,求出导弹的待增速度vg;最后,控制导弹的推力方向,使加速度a的方向与速度vg的方向一致,当待增速度vg=0时,控制发动机关机,完成闭路制导。

虚拟目标计算时,根据标准弹道对再入阻力和地球扁率进行修正,理论上所求的虚拟目标存在偏差。当导弹飞行中与标准弹道偏差较大时,虚拟目标就会发生较大改变,使用射前装订的虚拟目标会产生较大的偏差[23]。虚拟目标是导弹发射前确定的,导弹发射之后,如果需要变换打击目标,地面难以根据导弹的实时位置和新目标点计算出新的虚拟目标,因此,传统的闭路制导方法在弹道导弹发射之后难以满足变换打击目标[4]的需求,制约着弹道导弹的机动作战能力。

文中提出了一种基于落点的需要速度求解方法,需要速度求解过程中不需要依赖虚拟目标,精度较高,目标点只需在可攻击区域内即可,能够支持导弹变换打击目标。

1 基本思想

基于落点的需要速度求解方法的基本思想是:假设导弹以当前飞行状态关机,导弹的落点为L,以地心O过发射点F矢量L1和地心O过落点L矢量L2求出导弹的绝对弹道面[1]S1,以面S1的法向量n1与地心O过目标点M的矢量L3求出平面S2,假设导弹的落区的平均高程为h,R为地心到地面任意点的距离,联立面S1、S2,R+h,求解交点,在两个几何交点中,一般取北半球上的交点为真实交点。具体求解思路及参数关系如图1、图2所示。

图中,F为导弹在空中的某一初始位置,L为导弹在当前位置以当前速度自由飞行的落点,M为目标点,J为面S1、S2与地表的交点,绝对弹道面S1为惯性坐标系下地心O、起始点F、落点L构成的平面。ΔL为交点J与导弹落点L的大地线距离,ΔH为交点J与目标点M的大地线距离,A1为交点J与目标点M之间的大地方位角,A2为交点J与落点L之间的大地方位角。

图1 宏观示意图

图2 具体参数示意图

求解需要速度时,首先判断ΔL、ΔH的正负,再利用步长加速法对导弹当前速度进行迭代,不断改变导弹初始位置的速度值,最终使纵横向偏差小于ε(ε为迭代的偏差限制条件),此时初始位置的速度就为导弹在当前状态下打击目标M的需要速度。

2 模型建立

2.1 导弹的运动模型[5]

在发射坐标系中,建立导弹的被动段运动方程,考虑地球扁率和自转的影响,导弹受到空气动力、柯氏惯性力、牵连惯性力和地球引力的作用[6],导弹的质心运动方程为:

(1)

2.2 需要速度的求解模型

空间中过任意两点的弹道有无数多条,为了确定唯一弹道需要规定限制条件,一般的方法是给定速度倾角ϑk或者给定导弹的飞行时间Tm,为了便于计算,文章在进行仿真时给定速度vy的值,不加改变。基于落点的需要速度求解方法具体求解步骤如下:

1)设导弹在空间某一点F(x,y,z),速度为(vx,vy,vz),目标点为M(xm,ym,zm),导弹以当前速度关机时导弹的落点为L(xl,yl,zl)。计算S1、S2与地表的交点为J(xj,yj,zj),通过交点J计算纵横偏差ΔL和ΔH,判断ΔL、ΔH的大小,如果满足偏差限制条件|ΔL|<ε、|ΔH|<ε,此时导弹的速度(vx,vy,vz)就是所求的导弹对目标M的需要速度,如果不满足则进行步骤(2)。

2)当导弹当前速度不能满足要求时,进行迭代修正当前速度。首先根据目标点与绝对弹道面的位置关系,判断ΔL、ΔH的正负,然后利用变步长法进行迭代,求解vx的增加量Δvx1、Δvx2,vz的增加量Δvz1、Δvz2,令vx=vx+Δvx1或vx=vx+Δvx2,vz=vz+Δvz1或vz=vz+Δvz2,将此时的vx、vz一起代入被动段弹道进行弹道解算。

3)重复步骤1)、2),直到满足精度要求,迭代停止,输出需要速度。

基于落点的弹道导弹需要速度求解流程如图3所示。

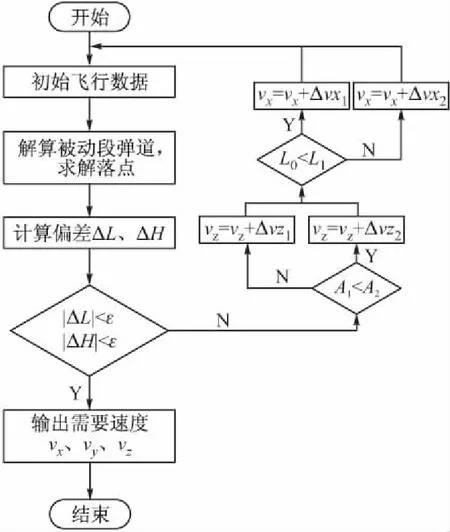
图3 需要速度的求解流程图

图3中,L0为起始点F到落点L的射程,L1为起始点F到落点M的射程[7];Δvx1、Δvx2为变步长法求得的x轴方向速度迭代值;Δvz1、Δvz2为变步长法求得的z轴方向速度迭代值。

3 仿真分析

文中假设一种洲际弹道导弹作为基础进行仿真,设导弹飞行中的初始位置坐标为(E121°00′00″,N35°00′00″),高程为100 km,初始瞄准方位角AT=1.0 rad,导弹的当前速度为(1 500 m/s,1 000 m/s,5 m/s)。为了便于计算,规定导弹在惯性坐标系下的速度vy保持不变,导弹目标点的高程为2 000 m,迭代要求的偏差限制条件为ε=10 m。下面给定不同目标点,求解导弹在当前位置对不同目标的需要速度,如表1所示。

表1 不同目标点的需要速度求解表

仿真结果表明,该方法能够有效求得导弹的需要速度,速度较快,对于目标的位置没有要求,且通过迭代求解的需要速度有较高的精度。

图4 vx随目标点纬度B的变化曲线

图5 vz随目标点纬度B的变化曲线

图6 vx随目标点经度L变化曲线

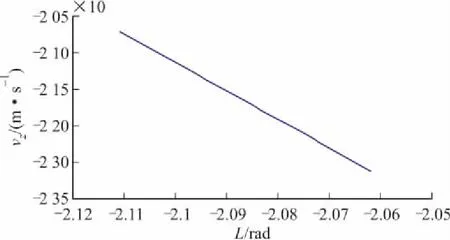
图7 vz随目标点经度L的变化曲线

图8 vx随空间位置x的变化曲线

目标的位置和当前位置发生变化时,导弹的需要速度也随之发生变化。下面仿真研究在目标经纬度、起始点空间位置变化时需要速度的变化规律。在图4～图7中,经纬度用弧度表示,图8、图9中,空间坐标x为地心直角坐标系中的坐标。

图9 vz随空间位置x的变化曲线

仿真结果表明,在此初始位置不变的情况下,在目标点位置发生变化时,导弹的x轴、z轴方向速度成线性变化[8],并且线性程度较好。目标的位置不变,导弹在空间的初始位置发生变化时,导弹x轴、z轴方向速度的变化呈现较好的线性。

4 结束语

文章分析现有的闭路制导方法,根据传统“需要速度”的求解方法及其特点,提出了基于落点的需要速度求解方法。该方法能够有效地求解导弹在空中某一初始状态下针对某一目标的需要速度,不需要求解虚拟目标,计算精度较高;目标的位置可以在允许区域内变化,导弹能够实现变换打击目标。因此,该方法具有一定的工程应用价值和前景。

该方法的缺点是计算量较大,对弹上计算机的性能要求高。为了解决计算量大的问题,下一步可针对某一型号的弹道导弹进行研究,分析导弹需要速度随空间位置、目标点位置改变的变化规律,利用需要速度变化规律线性强的特点,求解需要速度的插值多项式,然后将网格节点的需要速度信息和插值多项式参数存储到弹上,那么,当导弹飞经该区域时,就可以调用网格节点信息,利用插值多项式求解导弹实时的需要速度。这样就能够保证导弹在大范围机动时保持较高的精度,并具备一定的变换打击目标的能力。

[1] 肖龙旭,王顺宏,魏诗卉.地地弹道导弹制导技术与命中精度 [M].北京:国防工业出版社,2009:180-216.

[2] 王继平,王明海.基于虚拟目标点制导的误差分析 [J].飞行力学,2007,25(4):50-53.

[3] 王明海,李邦杰,刘新学.弹道导弹线性制导方案改进方法研究 [J].飞行力学,2003,21(2):38-40.

[4] BOGLER P L.Tracking a maneuvering target using input estimation [J].IEEE Transactions on Aerospace and Electronic Systems,1987,AES-23(3):298-310.

[5] 张毅,肖龙旭,王顺宏.弹道导弹弹道学 [M].长沙:国防科技大学出版社,2005:99-157.

[6] 马瑞萍,肖凡,张涛.一种基于速度倾角的闭路制导方法 [J].航天控制,2012,30(1):6-9.

[7] 熊介.椭球大地测量学 [M].北京:解放军出版社,1988:67-90.

[8] 邓建中,刘之行.计算方法 [M].2版.西安:西安交通大学出版社,2001:119-148.

SolutionofRequiredVelocityofBallisticMissileBasedonPointofFall

FAN Jinlong,LIU Xinxue,WU Jian,LIU Qingguo

(Rocket Force University of Engineering,Xi’an 710025,China)

In order to improve the solution accuracy of required velocity and solve the required velocity under the condition that the flight status and target location were uncertain,in this paper,a method based on point of fall for required velocity calculation was presented.In inertial coordinate system,the solving model of required velocity was established,the vertical and horizontal deviations between the object point and the absolute ballistic plane of ballistic missile were revised and the required velocity in current flight state was calculated.The simulation results indicated that this method could effectively solve the required velocity of missile in a certain fligh state with higher accuracy,and the targets could be changed properly.

ballistic missile; point of fall; absolute ballistic plane; required velocity; change objective

10.15892/j.cnki.djzdxb.2017.02.010

2016-05-17

范金龙(1990-),男,山东安丘人,硕士研究生,研究方向:飞行器总体、结构分析与飞行力学。

TJ762.2

A