远场水下爆炸作用下平板的冲击响应仿真*

辛春亮,王新泉,涂 建,王 伟,叶志萍

(1 北京航天长征飞行器研究所,北京 100076; 2中国航天员科研训练中心,北京 100094)

远场水下爆炸作用下平板的冲击响应仿真*

辛春亮1,王新泉1,涂 建1,王 伟1,叶志萍2

(1 北京航天长征飞行器研究所,北京 100076; 2中国航天员科研训练中心,北京 100094)

为了对舰船水下防护结构设计提供参考,采用LS-DYNA软件中的声固耦合法对远场水下爆炸作用下平板的冲击响应问题进行了模拟,计算结果与公认的双渐进近似算法计算结果较为接近。计算模型中采用了空化声单元和粘性非反射边界,并对比了网格加密、不同水柱高度和是否考虑空化的影响。LS-DYNA的声固耦合法计算速度快,计算准确度接近公认的双渐进近似算法,为国内水下爆炸数值计算人员提供了一种新的思路和计算工具。

LS-DYNA软件;远场水下爆炸;粘性边界条件;数值模拟

0 引言

舰船在水下爆炸下的结构响应一直是舰船设计者最为关心的问题,为此国内外进行了大量实船水下爆炸试验。水下爆炸试验耗费大、组织时间长、限制多,还会带来很多环境问题。随着计算技术的发展,研究者们逐渐转向采用数值计算来解决实船水下爆炸问题。

1 远场水下爆炸数值计算方法

根据舰船结构的受力状态,水下爆炸可分为近场和远场水下爆炸。在远场水下爆炸中舰船结构只发生弹性变形,气泡效应通常可以被忽略,数值计算模型中可只考虑冲击波和空化加载。LS-DYNA是LSTC公司推出的通用显式动力分析程序,该软件有多种算法可用于水下爆炸数值模拟,如流固耦合法、LOAD_SSA、LS-DYNA/USA等[1]。

流固耦合法主要用于近场水下爆炸计算。由于计算耗费和计算准确度的原因,难以用于远场水下爆炸模拟。这种方法需要将从爆源至结构、结构附近很大范围的流体划分网格,爆源附近的网格需要尤其细密,否则会抹平冲击波峰值,如此一来,计算模型将极其庞大。此外,EULER和ALE算法本身的耗散效应也会抹平冲击波峰值,使之传播失真。

LOAD_SSA可以用来模拟远场水下爆炸对结构的响应。这种方法可以考虑球面入射波、反射波、辐射波以及附带水质量带来的影响。由于不需要建立流体网格,这种方法计算速度很快,缺点是附带水质量没有考虑主冲击波过后后续流体的空化特性。

目前流体动力学计算软件更多采用有限元和非反射边界来模拟远场水下爆炸问题。这种方法可称之为声固耦合法,流体为线性声学介质,采用有限元模拟,在非反射边界处波可以无反射地透射出去。例如常用的有限元和边界元耦合法,在LS-DYNA中称之为LS-DYNA/USA模块,这种方法在流体边界上采用双渐进近似算法(DAA),可以考虑附带水质量的影响,计算准确度很高,但这种方法计算附带水质量矩阵时,需要不断对非稀疏矩阵求逆,计算耗费较大,计算时间较长。目前国内研究者仍然难以获得LS-DYNA/USA模块。

LS-DYNA中另一种非反射边界为粘性边界[2],这是一种局部近似非反射边界,最早由Lysmer和Kuhlemeyer[3]提出用来解决土壤和结构相互作用问题,后来Cohen和Jennings[4]又做了进一步的研究。对于入射压力波,粘性边界算法计算每个边界节点的法向应力和切向应力,在每个节点匹配入射应力,由此得到的反射应力为零。

σnorm=-ρcdvnorm

τshear=-ρcsvtan

(1)

式中:σnorm是边界法向应力;τshear是边界切向应力;ρ是材料密度;cd是畸变波速;cs是膨胀波速;v是质点速度。

为了模拟流体中的空化效应,水域采用空化声单元(CAFE)。空化声单元将流体域看做带有双线性状态方程的声学域,假定密度变化很小,只有畸变波可以在流体中传播,这就意味着当粘性边界用于流体边界时只需匹配σnorm。在流体中忽略粘性,流体的应力状态可以描述为流体的总压力p,这样当粘性边界施加在流体网格边界时,压力可采用如下简化形式:

p=-ρcvnorm

(2)

式中c是流体声速。

粘性边界可较为精确的处理法向入射波[3],但当入射角度从90°降到0°时精度急剧下降。此外,这种边界不考虑附带水质量,在附带水质量显著影响舰船响应的问题中计算精度不如双渐进近似算法。然而式(2)采用平面波假设形式,平面波假设均施加于水下爆炸早期阶段,因此对于空化声单元模型早期响应,粘性边界与双渐进近似算法的计算结果差别不会很大,但计算速度要快得多。

2 Bleich-Sandler平板问题

Bleich-Sandler平板问题是一个非常经典的考虑空化效应的远场水下爆炸验证算例[5-6]。在该问题中,平板浮于3.81 m高水柱的自由面上,平板和水域只允许垂向(Z向)运动。模型尺寸、材料参数见表1、表2和图1。

采用8节点声单元在水柱X、Y、Z三个方向分别划分100、1、1个网格,即流体网格尺寸为边长0.038 1 m的正方体,采用声学材料MAT_90来模拟流体。为了模拟无限水域,水域底部施加粘性边界条件。采用一个Belyschko-Tsay壳单元来模拟平板,材料模型为线弹性。

表2 平板几何尺寸和材料参数

图1 Bleich-Sandler问题示意图

在LS-DYNA声固耦合法中,耦合界面处的流体和结构网格可以采用3种方式:1)共节点;2)网格一一对应耦合;3)网格不匹配耦合。这里采用第二种一一对应的耦合方式。为了计算稳定,声固耦合时,流体单元尺寸须满足:

(3)

式中:ρ是流体密度;D是流体声单元在垂直于结构湿面方向上的厚度;ρs是结构密度;ts是结构单元厚度。

输入载荷为以指数形式衰减的平面入射冲击波,见式(4),输入点冲击波参数如表3所列。零时刻计算程序根据输入载荷和式(4)初始化流体压力,冲击波波前位于距平板湿面一个流体单元的节点处。这样做的优点是不用计算入射波在流体中的传播,避免了冲击波传播失真和能量耗散。

表3 Bleich-Sandler问题中入射波参数

(4)

式中:p0是输入点冲击波峰值超压;τ是时间常数。

3 粘性边界算法与双渐进近似算法计算结果对比

图2是平板垂向速度计算结果,图中还叠加了采用双渐进近似边界[2]时的计算曲线,该计算结果已经过验证。与双渐进近似边界条件相比,采用粘性边界条件时,平板最大速度略低,空化加载前负向最大速度也存在差异,除此以外两条曲线其他部分吻合较好。产生这些差异的原因是双渐进近似算法边界条件考虑了附带水质量而粘性边界条件未考虑。

图2 分别采用双渐进近似和粘性边界条件时平板垂向速度

图2中,采用粘性边界条件时计算曲线峰值过后存在轻微伪震荡,伪震荡与在有限元模型考虑空化效应有关。图3是不同网格密度的计算结果,可以看出网格加密后曲线更为光滑,噪音很低,而峰值几乎没有变化,但空化加载时间提前。网格加密到2和4倍原始网格后,曲线B和C几乎重合,这说明,网格加密到一定程度后,计算结果趋于收敛。

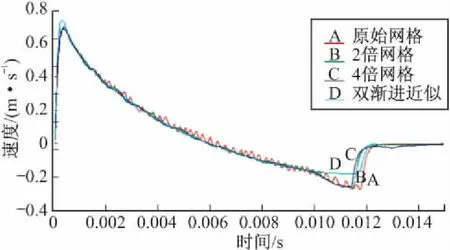
图3 采用不同网格密度时平板垂向速度

在远场水下爆炸问题中,船体的整体运动受附带水质量的影响。由于非反射边界不考虑附带水质量效应,这就需要流体域足够大,能够包含全部附带水质量。图4是计算模型中考虑不同水柱高度时的计算结果。在这些计算模型中,流体长度方向网格数量分别为50、100、200和400,即流体网格尺寸不变。由图可见,水柱长度越小,与双渐进近似算法计算结果偏差就越大。曲线C和D对应的水柱长度分别为7.62 m和15.24 m,这两条曲线几乎完全重合,与双渐进近似算法计算曲线也非常接近。这说明,随着水柱长度的加大,粘性边界条件不考虑附带水质量的缺陷逐渐被抵消,计算结果趋于收敛。

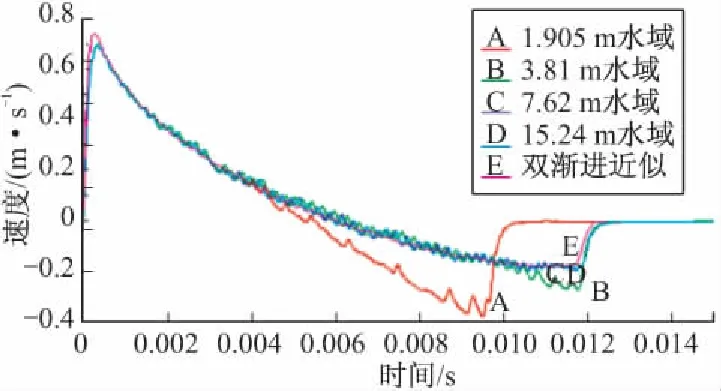
图4 不同水柱高度时平板垂向速度

空化加载对舰船结构影响较大,如图5所示。由于平板最大速度由主冲击波决定,所以是否考虑空化对此没有影响。而不考虑空化时平板速度在峰值过后很快衰减为零,且没有负向速度。

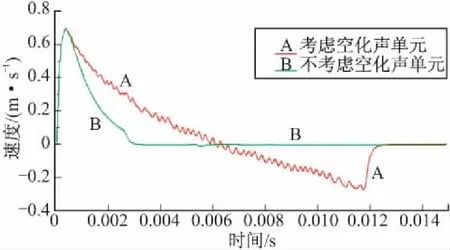
图5 考虑和不考虑空化时平板垂向速度

图6是水域空化时空图,对应计算模型的水柱长

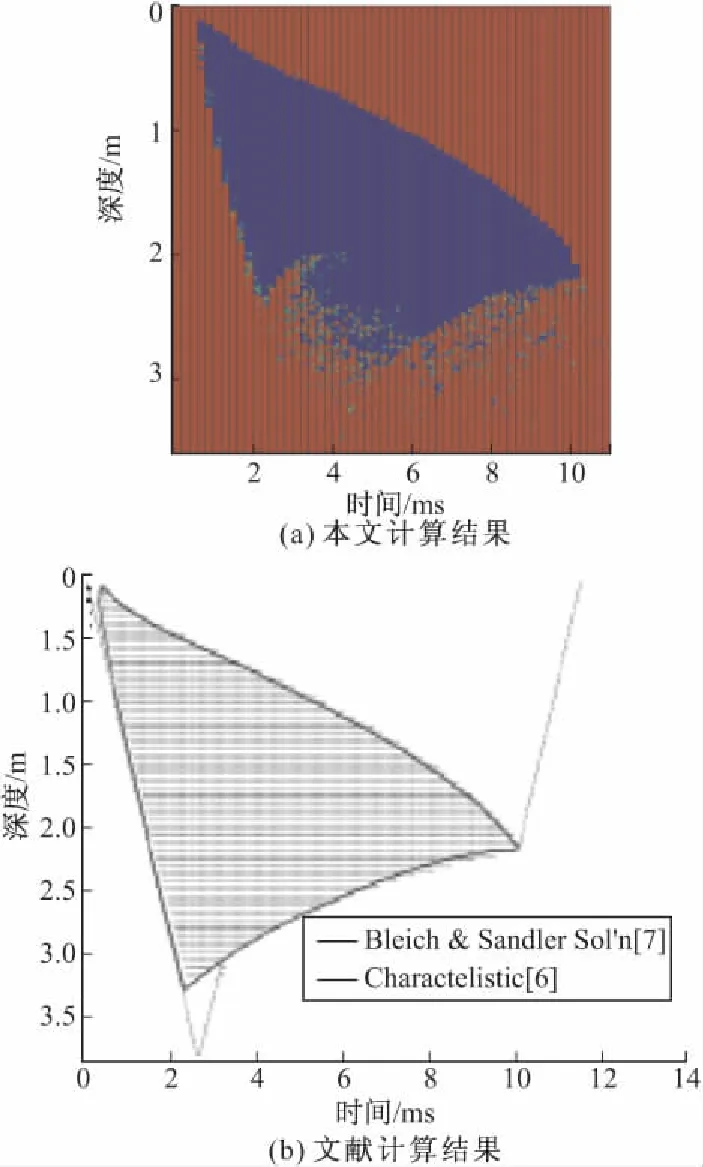
图6 水域空化时空图

度为7.62 m、流体长度方向网格数量为400。空化形成和闭合时间大约在0.4 ms和10.1 ms。图6(a)形状与图6(b)文献[6-7]计算结果大致吻合。图6(a)中,空化时空区上边界非常清晰,由于气泡和水混杂在一起,下边界较难明确分辨。在空化出现的时间段内,空化并未延伸到平板底部,平板和空化带之间始终存在未空化水的堆积区。空化带上、下边界收敛闭合在一起时空化溃灭,对应的时空位置为(10.1 ms,2.2 m)。图7是距离平板底部2 m处水单元压力曲线,曲线中第一个压力峰值是入射波将要抵达平板底部时该单元的压力,第二个峰值是衰减后的入射波和平板反射波的叠加形成的,随后由于平板运动导致水中压力急剧下降为空化压力,9.9 ms时刻由于空化闭合,压力又迅速回升。

图7 距平板底部2 m处水单元压力曲线

4 结论

文中介绍了LS-DYNA中的声固耦合法,并采用该方法对Bleich-Sandler平板问题进行了模拟。声固耦合法采用粘性非反射边界,主要考虑冲击波和空化加载,不计及气泡脉动和附带水质量。当计算水域取值较大时,LS-DYNA中的声固耦合法能够较为准确的预测远场水下爆炸下平板的响应。声固耦合法内嵌于LS-DYNA软件中,适合于远场水下爆炸分析,计算效率高,这种分析方法可为国内水下爆炸仿真人员和舰船设计者提供参考。

[1] 辛春亮,秦健,刘科种,等.基于LS-DYNA软件的水下爆炸数值模拟研究 [J].弹箭与制导学报,2008,28(3):156-158.

[2] KLENOW B,BROWN A.Assessment of non-reflecting boundary conditions for application in far-field UNDEX finite element models[C]// 77th Shock and Vibration Symposium.Monterey:SAVIAC,2006.

[3] LYSMER J,KUHLEMEYER R L.Finite dynamic model for infinite media [J].Journal of Engineering Mechanics Division,1969,95(4):859-878.

[4] CHOEN M.Silent boundary methods for transient wave analysis:PB82-201831[R].1983.

[5] MAIR H U.Benchmarks for submerged structure response to underwater explosions[J].Shock and Vibration,1999,6(4):169-181.

[6] BLEICH H H,SANDLER I S.Interaction between structures and bilinear fluids[J].International Journal of Solids and Structures.1970,6(5):617-639.

[7] SPRAGUE M A,GEERS T L.Computational treatment of cavitation effects in near-free-surface underwater shock analysis [J].Shock and Vibration,2001,8(2):105-122.

NumericalSimulationofPlateResponseSubjecttoFar-fieldUnderwaterExplosion

XIN Chunliang1,WANG Xinquan1,TU Jian1,WANG Wei1,YE Zhiping2

(1 Beijing Institute of Space Long March Vehicle,Beijing 100076,China; 2 China Astronaut Research and Training Center,Beijing 100094,China)

Acoustic-structure interaction method in LS-DYNA software was used to solve plate response subject to far-field underwater explosion.Cavitation acoustic finite element (CAFE) and non-reflecting boundary were used in UNDEX models.Results with different fluid mesh density,different length of fluid column,with or without CAFE effects were compared with DAA results.This kind of method could offer significant savings in computational time over DAA without greatly affecting accuracy of results.

LS-DYNA software; far-field underwater explosion; viscous boundary condition; numerical simulation

10.15892/j.cnki.djzdxb.2017.02.019

2016-06-12

辛春亮(1973-),男,山东日照人,研究员,博士,研究方向:战斗部设计和数值模拟。

TG156

A