间隔纸靶测试弹丸章动试验数据拟合分析*
倪庆乐,王雨时,闻 泉,张志彪,李作华
(1 南京理工大学机械工程学院,南京 210094; 2 辽宁华兴机电有限公司,辽宁锦州 121017)
间隔纸靶测试弹丸章动试验数据拟合分析*
倪庆乐1,王雨时1,闻 泉1,张志彪1,李作华2
(1 南京理工大学机械工程学院,南京 210094; 2 辽宁华兴机电有限公司,辽宁锦州 121017)
针对引信技术关注的火炮外弹道起始段弹丸章动规律问题,结合理论分析得到的数学模型,利用MATLAB拟合间隔纸靶试验得到的章动数据,得到外弹道起始段弹丸章动规律半经验表达式。该方法解决了纸靶法离散化测试数据处理和判读问题,可较准确得出章动周期,并解决传统章动测试离散化数据无法给出最大章动角真值且系统偏小的问题。
外弹道学;数值拟合;章动规律;章动角;经验公式
0 引言
弹丸章动角及章动角速度测量对于武器弹药外弹道研究,尤其是对研究弹丸自由飞行状态下的气动特性、飞行稳定性和武器散布精度均有重要意义。目前章动角随弹道弧长变化规律测试基本上采用高速摄影、狭缝摄影和间隔纸靶方法。高速摄影和狭缝摄影方法受设备所限应用较少,且因所得照片小又不清晰,难以定量判读。间隔纸靶法应用较为普遍,但其穿孔边缘破碎后长短轴判读很难准确,测试精度较差。此外,实验中测得的数据均为离散数据,传统数据处理方法[1]将最大章动角直接取为测得离散数据中的最大值具有一定的偶然性。
文献[2]通过室内模拟试验方法,定量解决了在外弹道姿态测量时对所测值准确度不确定的状况,确定了狭缝像机动态角度测量误差为0.1°。文献[3]提出采用非接触式光学立靶测量原理测量弹丸章动周期的方法,测量结果表明:此方法可解决狭缝像机不能实时测量且使用繁琐的问题。文献[4]对弹丸飞行姿态进行了运动学分析,其中涉及到旋转稳定弹丸和尾翼稳定弹丸的章动规律:旋转稳定弹的攻角不断减小,弹头运动曲线为幅值不断减小的外摆线;非旋转尾翼弹的攻角幅值按指数规律衰减,且周期逐渐增大,总体趋势作平面阻尼运动;旋转尾翼弹复攻角曲线为内摆线,但文中未对推导结论做试验验证。文献[5]提出一种数字化图像采集与处理纸靶弹孔方法,对纸靶法获取的弹孔图像进行数据判读以测量弹丸飞行状态参数,结果表明:对于章动角大于5°的情况,测量精度优于0.2°;章动角介于1°~5°时,测量精度优于0.5°。目前所见文献主要是针对弹丸章动测试方法以及理论推导的研究,尚未见基于实验测试数据的章动规律分析。
文中基于章动实验测试数据,利用MATLAB拟合弹丸章动规律,为弹丸飞行过程中的弹载装置受力计算提供依据。
1 章动角实验数据的曲线拟合
根据已有外弹道理论推导的章动角规律,初步假设章动角拟合曲线为平面曲线:
(1)
式中:A是与章动角幅值有关的系数;B是章动角幅值衰减速率;C是章动周期;D是章动角周期衰减速率;E是章动角曲线左右平移的距离;F是动力平衡角。
根据某76 mm口径火炮杀伤爆破弹章动角测试数据,按最小二乘法原则,应用MATLAB对数据进行拟合,得到的章动角拟合曲线各参数如表1所列。表中的和方差是拟合数据和原始数据对应点的误差的平方和,其越接近于0说明模型选择和拟合得越好,数据预测也越成功。
实验测得的章动角数据与其拟合曲线对比如表2所列。

表1 章动角拟合曲线各参数

表2 实验测得的章动角数据与拟合曲线的对比
由表2中数据可以看出:依据经验推算出的纸靶摆放位置合理,能较好地反映章动角的变化趋势。但第1、2、4、5发的拟合曲线在炮口附近的章动角为负值,这是没有意义的,原因或为弹丸出炮口时受到的起始扰动较大,致使弹道起始段章动规律不符合曲线。第1、2、4、5发的拟合曲线的最大值,即拟合的最大章动角小于测得的最大章动角,且第1、4发的拟合曲线的最小值为负值,显然这也是不符合实际的。因此,将第1、2、4、5发的拟合曲线的最大值固定为测得的最大值,将第1、4、5发的拟合曲线的最小值定为实测结果再次进行拟合,得到的拟合曲线参数如表3所列。实验测得的章动角数据与固定最大值的拟合曲线对比见表4。

表3 拟合曲线最大值固定为测量最大值时的各拟合参数
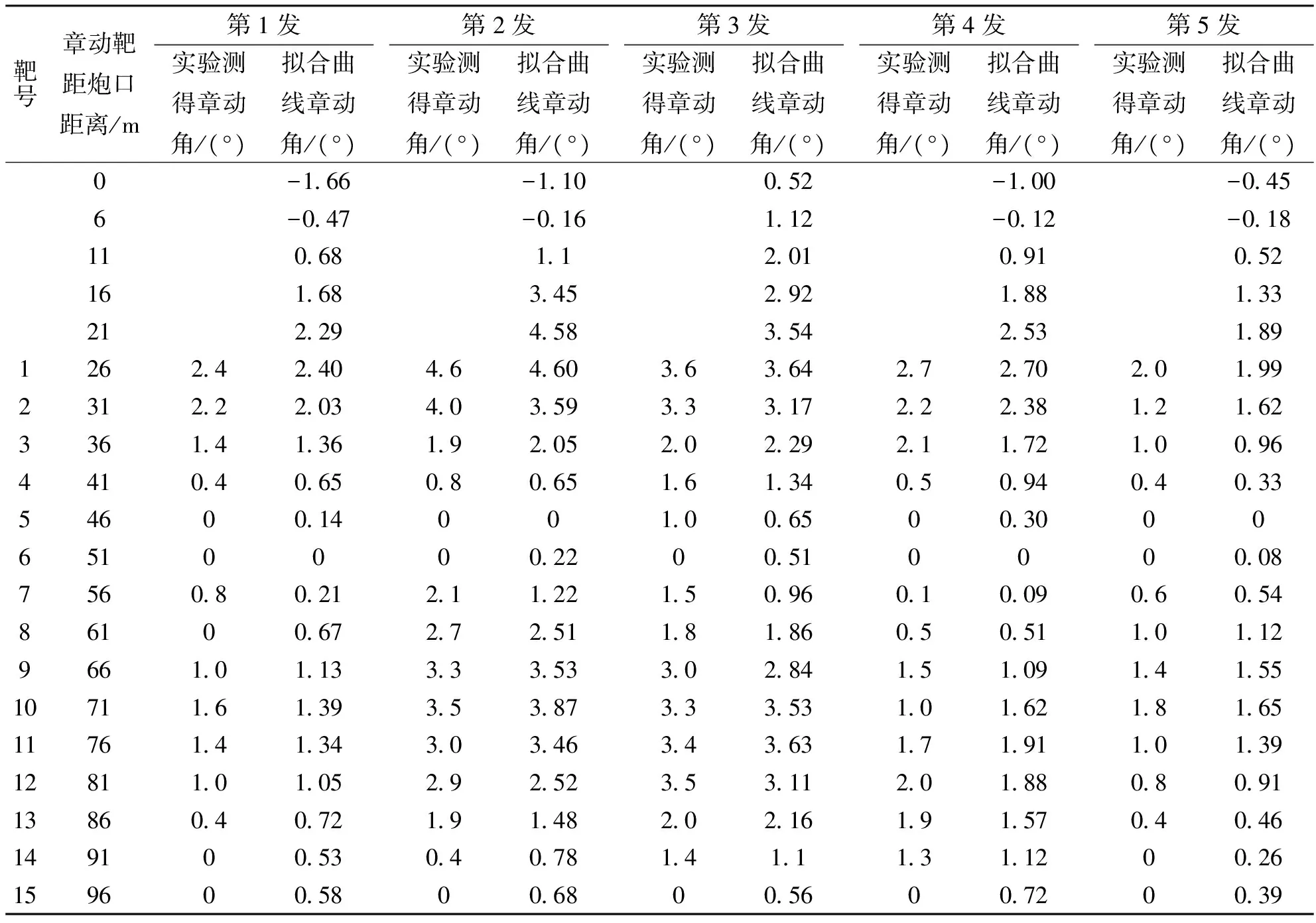
表4 实验测得的章动角数据与固定最大值的拟合曲线对比
文献[6]中指出:在弹丸飞行过程中,起始扰动、不对称因素、风、底排工作不正常、燃烧流动规律变化等因素有可能引起章动角增大。因此,将拟合曲线设定为:
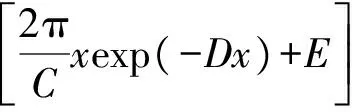
(2)
式中G为表示章动角随射程增大的系数。进一步对实验数据进行分析,拟合结果如表5所列。不同关系式假设条件下拟合参数A、F与最大章动角的关系如表6所列。弹丸章动角实验数据描点曲线与按式(2)给出的拟合曲线如图1所示。
由于间隔纸靶试验得到的章动角数据为离散值,所以不一定能恰好反映最大章动角。而由表5可看出,按式(2)对试验数据进行拟合后得到的最大章动角均大于试验测得的最大章动角,说明按式(2)拟合可解决传统章动测试离散化数据无法给出最大章动角真值且系统偏小的问题。

表5 假设章动角增大时拟合曲线各参数
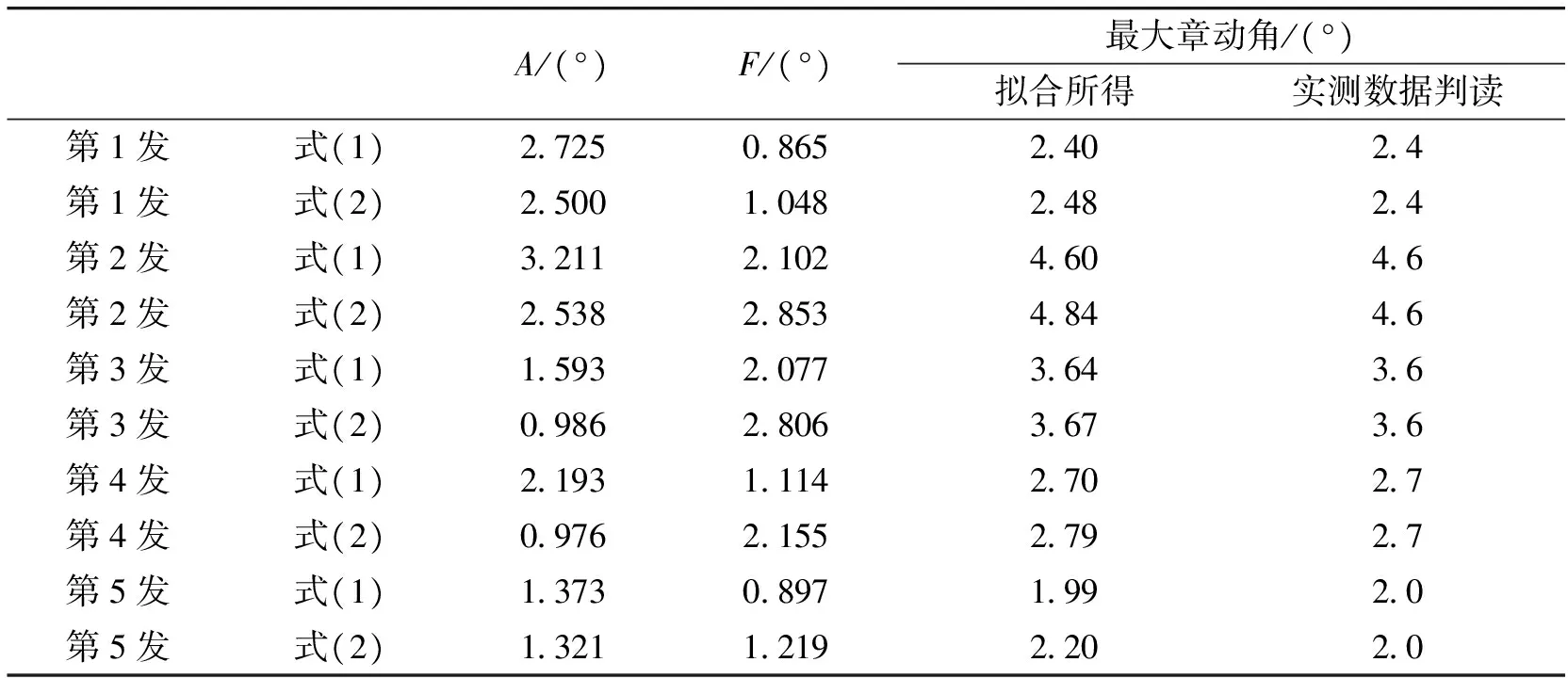
表6 不同关系式假设条件下拟合参数A、F与最大章动角的关系

图1 弹丸章动角实验数据描点曲线与拟合曲线
而由图1各曲线可看出:第1、5发的拟合曲线第二个峰值略小于实际测量值,原因或为纸靶摆放位置误差或靶孔测量误差。
2 分析和讨论

b)实测5发数据的最大章动角范围是2.0°~4.6°,散布较大。由于样本量较少,所以难以进行统计学处理。而对应最大章动角的情形是一种极限弹道环境,故很有必要加大章动角测试样本量至20发以上。
c)如表1和表3所列,式(1)中的拟合参数B>0,且B≈0,说明弹丸飞行初始段章动角幅值略有衰减,但衰减较为缓慢。
d)从表1、表3和表5可以看出,76 mm口径火炮榴弹章动角衰减周期范围为41.91~65.00 m,变化范围达47%。该衰减周期大小与章动角幅值无关。由于对应最短章动周期的情形也是一种极限弹道环境,所以从这个意义上讲加大章动角测试样本量也是很有必要的。
e)如表1和表3所列,式(1)中的拟合系数D<0,且D≈0,说明弹丸飞行初始段章动衰减周期基本不变略有增长,但增长较为缓慢。
f)表3中的F值为弹丸章动时的动力平衡角,未见其值与章动角幅值有关。
g)如表5所列,式(2)中的拟合系数G<0,且G≈0,说明这5发弹丸章动角是收敛的,逐渐减小,并未发散。
h)如果靶场和弹炮系统试验条件允许,在弹丸初速较高、受拦截间隔纸靶影响较少的情况下,应尽可能多测更大距离(衰减周期)内的章动角数据,为准确预测弹丸章动角远距离上衰减规律和确定弹丸飞行是否有可能失稳提供参考。
3 结论
文中针对弹丸外弹道飞行过程中的章动规律问题,基于某76 mm口径火炮杀伤爆破弹章动角测试数据,依据最小二乘法原则,利用MATLAB软件进行拟合,拟合所得弹丸章动曲线与测试值较为符合,解决了纸靶法离散化测试数据的处理和判读问题,可较准确得出章动周期,并解决传统章动测试离散化数据无法给出最大章动角真值且系统偏小的问题。通过半经验表达式可确定外弹道初始段任意距离点的章动角数值,用于弹载装置如引信机构动态特性特别是引信弹道炸问题的理论分析和计算机仿真研究。
[1] 闫章更,祁载康.射表技术 [M].北京:国防工业出版社,2000:106-109.
[2] 施浣芳,刘群华.狭缝高速摄影章动角测量室内模拟设计 [J].高速摄影与光子学,1991,20(2):209-214.
[3] 高听,单长胜,李建安.弹丸章动周期的光学立靶测量法 [J].光子学报,2003,32(11):1386-1390.
[4] 张斐.弹丸飞行姿态运动学分析与模拟试验研究 [D].太原:中北大学,2013.
[5] 杜博军,李国荣,姜志.弹丸章动纸靶数据高精度处理方法 [J].弹道学报,2014,26(3):50-53.
[6] 郭锡福.火炮武器系统外弹道试验数据处理与分析 [M].北京:国防工业出版社,2013:128.
FittingDataAnalysisofProjectileNutationTestedbyIntervalPaperTarget
NI Qingle1,WANG Yushi1,WEN Quan1,ZHANG Zhibiao1,LI Zuohua2
(1 School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China; 2 Liaoning Huaxing Electromechanical Co.Ltd.,Liaoning Jinzhou 121017,China)
Fuse technology concerns projectile trajectory initial segment nutation law issues,semi-empirical expressions of nutation law were got in initial segment of projectile exterior ballistic by mathematical model,external ballistics theory obtained and MATLAB to fit the data.Processing and interpretation issues were solved for discrete test data paper target method obtained,and accurate nutation cycle can be obtained.The problem solved is traditional nutation test discrete data can’t give real maximum nutation angle and the system is too small.
external ballistics; numerical fitting; nutation law; nutation angle; empirical formula
10.15892/j.cnki.djzdxb.2017.02.035
2016-07-20
倪庆乐(1991-),男,河北衡水人,硕士研究生,研究方向:引信设计及其动态特性的研究。
TJ012.3
A

