义务教育课程标准与中考试卷一致性分析——以2013—2016年厦门市中考数学试卷为例

缪 琳，陈清华，苏圣奎



义务教育课程标准与中考试卷一致性分析——以2013—2016年厦门市中考数学试卷为例

缪 琳1，2，陈清华1，苏圣奎1，3

（1．福建师范大学数学与信息学院，福建福州 350117；2．上海市虹口实验学校，上海 200080；3．福建省厦门第六中学，福建厦门 361012）

基于义务教育数学课程标准的中考试卷分析与研究是了解当前新课程教育改革中国家课程设计与数学学业评价体系关联程度的新视角．以认知水平为核心维度，对厦门市中考数学试卷与义务教育数学课程标准进行基于“SEC”的一致性分析，发现它们之间不具有统计学上显著的一致性，二者差异较大．因此建议完善课程标准，规范课程评价体系，进一步开展多向一致性研究，促进学业考试的合理纠偏及教师的专业化发展．

课程标准；中考；一致性分析

1 引言

20世纪末，美国教育部与NISE合作，成立了课程与评价的一致性分析协会．21世纪初在上介绍了一系列的一致性研究成果，引起了全世界对一致性研究的重视和兴趣．中国关于课程标准的一致性研究起步较晚，目前国内关于“数学科一致性”定量研究主要是以借鉴韦伯分析模式和“SEC”分析模式为主，包括课程标准与评价的一致性研究、课程标准与教科书的一致性研究、课堂教学与学业评价一致性研究等诸多方面．在中国知网检索从2013年1月—2017年8月，以“课程标准一致性”为主题词的文章共735篇，以“课程标准一致性+数学”为主题词的文章共117篇，而涉及课程标准与评价，尤其是关于“课程标准与中考数学评价一致性”的研究仅6篇．可见义务教育初中数学学科在这个方面的研究较少．

“国家课程标准是教材编写、教学、评估和考试命题的依据，是国家管理和评价课程的基础．”[1]然而时至今日，基于标准的教学虽是当前课程改革的主流，可在实践操作中却屡屡受挫，其根源在于以初中升学为重心的学业水平考试（简称中考）是作为学业评价的主要手段，它对教学起着关键性的导向作用．“进行数学教育改革，应该改变传统的应试制度，采用在标准基础上的评价制度．”[2]“只有当评价这一最后的出口是基于标准的时候，教材编写和教师教学才有可能是基于标准的．”[3]因此学业评价与课程标准的一致性问题正成为国内外课程研究的重要方向．其研究，不仅提供了课程标准和评价是否吻合这一结果，而且研究过程能够帮助教师看到评价是如何与课程标准、课堂教学发生联系的，能更好地促进一线教师对课程标准与评价的理解．

2 研究过程

2.1 研究对象

以《义务教育数学课程标准（2011年版）》（以下简称《义务课标》）及2013—2016年厦门市中考数学试卷（以下简称厦门卷）为研究对象．

2.2 研究工具

判定和分析课程系统各相关要素吻合程度的理念、程序与方法的总和称之为“一致性分析范式”[4]．为了改变基础教育薄弱的状态，强化基于课程标准的评价，推进课程与评价的契合性，美国最早开始关于课程标准与评价的一致性研究，并研究出诸多一致性模式．“SEC”一致性分析是由美国学者安德鲁·帕特（Andrew Porter）和约翰·史密森（John Smithson）在韦伯一致性分析工具的基础上建立且应用最为广泛的分析模式之一．该模式以知识的广度和深度为框架进行搭建，建立统一评价标准．其中“知识广度一致性标准可以为我们探究内容标准中的主题范围与评价测试涉及的主题范围之间的相关性提供平台，知识深度一致性标准是分析评价与课程标准一致性的核心维度”[5]．

“SEC”分析模式通过对研究对象进行“知识广度”（即“内容主题”）和“知识深度”（即“认知水平”）的划分，构建以“内容主题”和“认知水平”为框架的二维矩阵；在该二维矩阵框架下对研究对象进行编码、统计，通过矩阵对研究内容进行标准统一的描述，利用该二维矩阵所产生的比率值数据进行计算；而后根据其匹配程度由一致性系数公式得到一致性系数，再根据统计学原理计算出该二维矩阵一致性系数的临界值，把所求得的一致性系数与临界值进行比对，从而判断其所比较对象在统计学意义上的一致性程度的强弱．

2.3 编码框架的确定

《义务课标》把课程内容划分为4个部分：“数与代数”、“图形与几何”、“统计与概率”、“综合与实践”[6]．其中“综合与实践”是在“数与代数”、“图形与几何”、“统计与概率”这3个模块中加以具体落实．为了将课程内容进一步细化统计分析，参考《上海市中小学数学课程标准（试行稿）》，将“数与代数”细分为“数与运算”、“方程与代数”、“函数与分析”3个知识模块[7]．从而将“内容主题”划分为“数与运算”、“方程与代数”、“图形与几何”、“函数与分析”、“数据整理与概率统计”等5个知识模块．

《义务课标》中对课程结果目标分为：了解、理解、掌握、运用．该认知水平的划分是以布鲁姆认知领域中的行为目标划分为基础，从简单到复杂，按照思维的种类和水平划分两种水平：记忆水平以及理解水平，并结合了研究对象的实践性、层次性、可操作性进行细分．综合考虑各种一致性模型的认知水平划分、国内对数学认知水平的划分实际情况、“SEC”认知水平维度的编码可操作性，认知水平划分采用《义务课标》认知水平的划分模式．即划分为“了解”（同义词：知道）、“理解”（同义词：会、会用、认识、识别）、“掌握”（同义词：能、能用）、“运用”（同义词：证明）等4个认知水平，这里将《义务课标》中的“探索”归为“掌握”，比如“探索不等式的基本性质”．

综上，构建“SEC”一致性分析模型如表1所示[8]：

表1 “SEC”一致性分析二维框架

2.4 对研究对象的整理及编码

对研究对象的整理与编码，是由3位具有研究生学历且有十多年教学经验的初中数学老师，经过“SEC”一致性分析模型编码培训基础上进行的．3位老师分别对2013—2016年厦门中考数学卷编制双向细目表，整理考点所属的知识邻域，厘清相应认知水平层次，进而对试题与《义务课标》进行编码．编码过程中相互之间存在异议的内容主题和认知水平通过多轮讨论、协商，并结合多位专家意见，最终达成共识，得到编码结果的原始数据（表2、表3）：

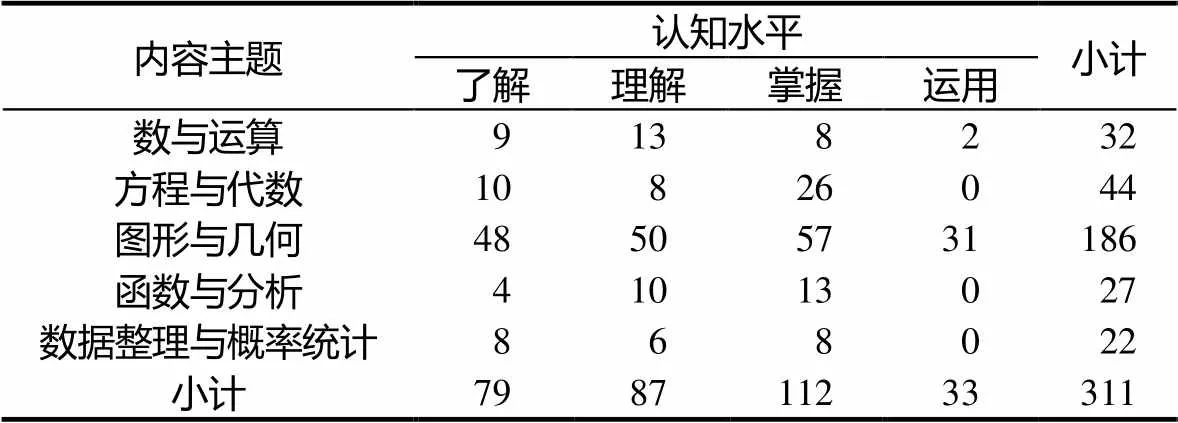
表2 义务课标原始数据

表3 2013—2016年厦门卷原始数据

3 研究结果

3.1 总体一致性系数情况

将上述原始数据转化为比率数据：即将表格中每个单元数据除以表格右下方总数据，得到每个单元格数据占总体数据的比率，其比率和为1；再将比率数据代入一致性系数公式，计算一致性系数，其一致性系数如图1所示．

可知，《义务课标》与2013—2016年厦门卷一致性系数均小于临界值0.914 2，二者之间不具有统计学上显著的一致性．为了更直观、全面、具体表现厦门卷与《义务课标》的差异，下面将通过曲面图、柱形图和折线图进行详细描述．

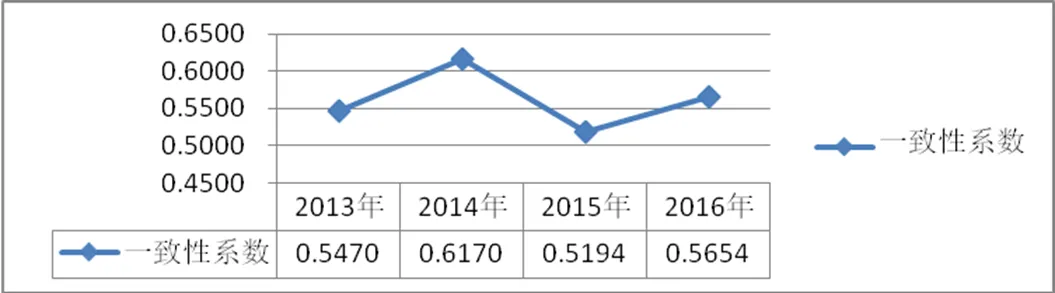
图1 2013—2016年厦门卷与义务课标一致性系数

3.2 总体一致性分布情况——曲面图分析

《义务课标》和厦门卷曲面图如图2、3、4、5、6所示．横坐标代表内容主题，纵坐标代表认知水平．横轴、纵轴的交点代表该内容主题下认知水平的权重，不同深浅的色块代表不同权重，越靠近中心区域则权重越大．（注：所有图形中，主题A——数与运算；主题B——方程与代数；主题C——图形与几何；主题D——函数与分析；主题E——数据整理与概率统计．）

图2 义务课标曲面图

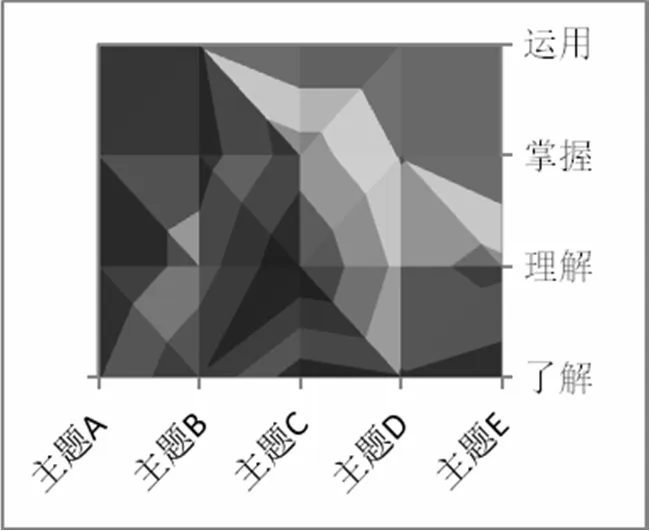
图3 2013年厦门卷曲面图

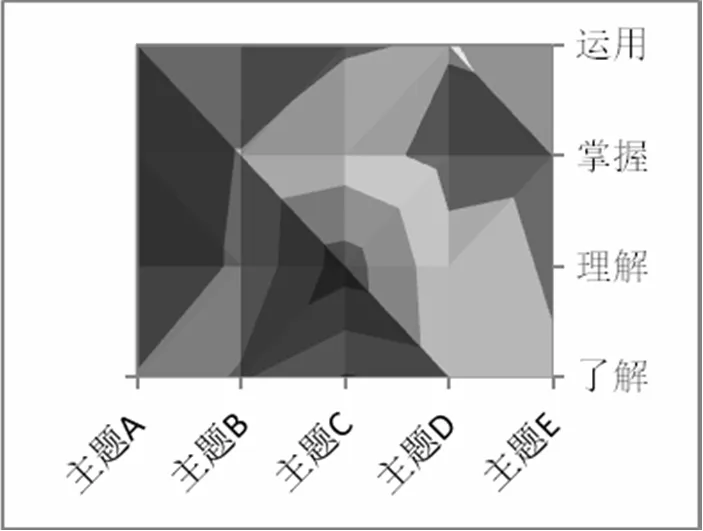
图4 2014年厦门卷曲面图

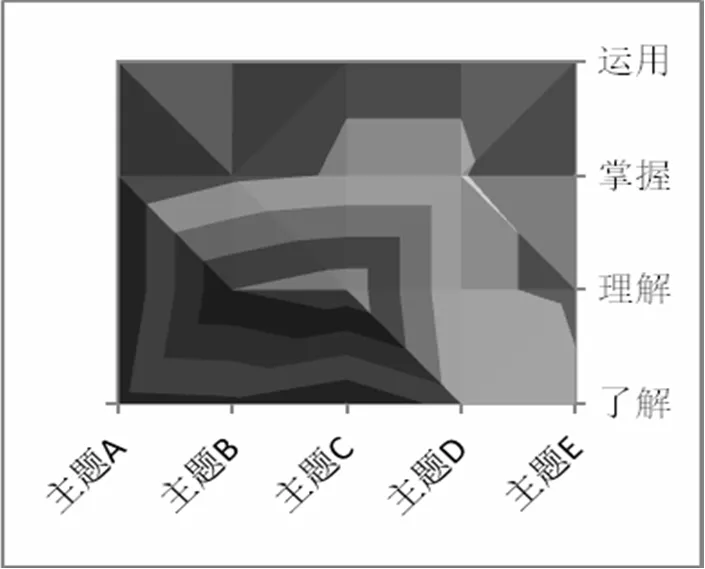
图5 2015年厦门卷曲面图

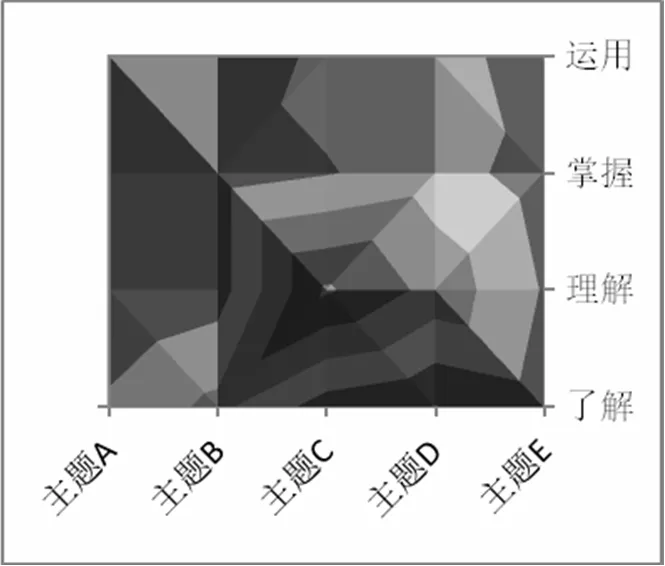
图6 2016年厦门卷曲面图

从上述图形形状可以看出厦门卷考查要求与《义务课标》要求有较大的差异．二者相比，不同点：考查重点不一致，厦门卷均侧重于“图形与几何”水平2考查，《义务课标》侧重点“图形与几何”水平3考查．相同点：厦门卷与《义务课标》在“数与运算”水平4、“方程与代数”水平4、“数据整理与概率统计”水平4的考查力度基本一致．

3.3 一致性分布情况——柱形图与折线图分析

为了具体呈现厦门卷与《义务课标》的一致性状态，将上述对象比率数据值按照内容主题和认知水平主题制作成柱形图并结合折线图加以分析（如图7）．

图7 义务课标与2013—2016年厦门卷柱形图

（1）认知水平1“了解”．

该认知水平下厦门卷知识点总数权重起伏较大（2013年0.280 0，2014年0.333 3，2015年0.200 0，2016年0.226 7），仅2013年、2014年考查力度高于《义务课标》要求（0.254 0）．具体情况如图8所示．

“数与运算”、“方程与代数”、“数据整理与概率统计”4年试卷考查力度均高于《义务课标》要求．“图形与几何”4年试卷考查力度均远低于《义务课标》要求．“函数与分析”前3年试卷考查力度均高于《义务课标》要求．

图8 义务课标与2013—2016年厦门卷折线图1

（2）认知水平2“理解”．

该认知水平下厦门卷知识点总数权重有所起伏（2013年0.473 3，2014年0.346 7，2015年0.533 3，2016年0.413 3），4年考查力度均高于《义务课标》要求（0.279 7）．具体如图9所示．

图9 义务课标与2013—2016年厦门卷折线图2

“数与运算”4年试卷均未进行考查，低于《义务课标》要求．“方程与代数”、“图形与几何”、“函数与分析”、“数据整理与概率统计”4年试卷考查力度均高于《义务课标》要求．

（3）认知水平3“掌握”．

该认知水平下厦门卷知识点总数权重起伏不大（2013年0.200 0，2014年0.200 0，2015年0.146 7，2016年0.173 3），但4年考查力度均远低于《义务课标》要求（0.362 7）．具体如图10所示．

图10 义务课标与2013—2016年厦门卷折线图3

“数与运算”4年均未考查，远低于《义务课标》要求．“方程与代数”、“图形与几何”4年考查力度均小于《义务课标》要求．“函数与分析”2014年考查力度处于最低，且低于《义务课标》要求，其余3年均高于《义务课标》要求．“数据整理与概率统计”2013年与2015年均未考查，2014年与2016年考查力度均高于《义务课标》要求，且2014年考查力度达到峰值．

（4）认知水平4“运用”．

该认知水平下厦门卷知识点总数权重呈现上升趋势（2013年0.046 7，2014年0.120 0，2015年0.126 7，2016年0.186 7），上述4年考查力度仅在2013年低于《义务课标》要求（0.106 1），其余3年均高于《义务课标》要求．具体如图11所示．

图11 义务课标与2013—2016年厦门卷折线图4

“数与运算”前3年未考查，仅2016年有所考查且考查力度高于《义务课标》要求．“方程与代数”《义务课标》对其没有考查要求，仅在2013年有所考查且考查力度高于《义务课标》要求，后3年试卷未考查．“图形与几何”2013年未考查，其余3年考查力度均低于《义务课标》要求．“函数与分析”《义务课标》对其没有考查要求，但仅2013年未考查，其余3年均考查，考查力度高于《义务课标》要求．“数据整理与概率统计”《义务课标》对其不做考查要求，2013年与2016年均未考查，其余两年均考查，考查力度高于《义务课标》要求．

4 研究结论

4.1 总体一致性情况

厦门卷与《义务课标》的一致性系数均远低于临界值，二者之间不具有统计学上显著的一致性．一致性水平程度为：“2014年”>“2016年”>“2013年”>“2015年”．

4.2 在内容主题上的一致性情况

不同点：厦门卷在“数与运算”、“图形与几何”4年考查力度均低于《义务课标》要求，尤其是“图形与几何”的考查力度远低于《义务课标》要求；“方程与代数”、“函数与分析”、“数据整理与概率统计”4年考查力度均高于《义务课标》要求，尤其以“函数与分析”的考查力度增幅最大．厦门卷与《义务课标》的次重点有所不同，《义务课标》侧重“方程与代数”主题，而厦门卷侧重点则在“方程与代数”及“函数与分析”主题之间交错考查，且均高于课标要求．

相同点：从知识内容的重视程度上，厦门卷与《义务课标》都一致地对“图形与几何”内容主题尤为重视．

4.3 在认知水平上的一致性情况

不同点：厦门卷与《义务课标》对认知水平各层级考查的重视程度不同，不仅表现在对认知水平重点考查项目不同，对各层级的重视程度也不相同．如认知水平2“理解”4年考查力度均远高于《义务课标》要求；水平3“掌握”4年考查力度均远低于《义务课标》要求．同时，考查重点也不一致，厦门卷侧重考查“图形与几何”的认知水平2“理解”，而《义务课标》侧重“图形与几何”的认知水平3“掌握”．厦门卷同《义务课标》相比：“数与运算”在认知水平1“了解”的考查力度加强；“方程与代数”在认知水平1和认知水平2上都有所加强，在认知水平3上减弱；“图形与几何”在认知水平2考查力度加大，且变化较大，在认知水平1、3、4上都有所减弱；“函数与分析”的考查整体都有所加强，认知水平1、2考查的力度大于认知水平3、4；“数据整理与概率统计”在认知水平1或认知水平2的考查力度上均有所加强．

相同点：厦门卷在认知水平1“了解”仅前两年高于《义务课标》要求，4年数据均值与《义务课标》要求基本一致；水平4“运用”仅头尾两年低于《义务课标》要求，4年数据均值与《义务课标》要求基本一致．

5 思考与建议

5.1 完善《义务课标》学业评价体系

中考数学试卷与《义务课标》一致性问题，促使研究者反思是否应该进一步完善《义务课标》中的学业评价体系，规范学业水平考试（中考），使得考试内容、评价体系更为规范、严谨．如果试卷与《义务课标》的一致性较差，将不利于基于课标的教与学的推进，将淡化课标的主导作用，影响课标的落实程度．鉴于中考数学试卷对日常教学的影响，建议开展多向研究，力求试卷与《义务课标》显著一致[7]．试题命制者在试卷命制的过程中尽量贴近《义务课标》，结合一致性研究方法改善命题技术、借鉴命题方法，通过研究相关因素的一致性，借鉴科学的量化比较方法，对存在显著差异的中考数学试卷进行纠偏和改进，使得中考是基于《义务课标》的考查，以更好的保证《义务课标》的全面有效落实．

5.2 建立与《义务课标》相一致的学业评价标准

厦门市自1981年成为国家经济特区以来，秉承“先行先试、敢闯敢试”的创新精神，不仅在经济发展上成果显著，其教育质量在福建省也是首屈一指．然而通过对其近4年的中考数学试卷与《义务课标》的一致性分析，其结果并不尽如意．崔允漷指出，“学业成就评价有两个目的．对外，要能满足公众问责的要求；对内，要能满足学生学习改善的要求．”[3]基于课标的课堂教学成为近年教育改革的大趋势，然而“学校对教师的评价、教师对学生的评价仍然以学生的考试成绩为主要依据，多元化的评价体系基本上形同虚设”[10]，这必将导致广大一线教师实施的是“基于中考的课堂教学”即“基于评价的教学”．而当“评价”远离课标，此时的“评价”还是否能真正促进学生的学业改善，提高学生的数学素养？因此，“建立与《义务课标》相一致的学业评价标准，特别是针对重点内容的评价标准，建立层次明确的评价指标体系，对改进学业评价具有重要的意义”[11]．

5.3 提高教师的专业化水平

“教师是决定教改成功与否的重要人力资源之一”[12]，一线教师实施基于《义务课标》的教学已成为课程改革的关键环节，课程改革的深化需要“合格的、新型教师即科研型教师”[14]．然而，教师随着教学年限的增长，教学经验逐步丰富，成长为经验型的教师，对中考的研究往往落实在对考题的解法和教法上，对试卷命题的合理性缺乏理论上的认识．“教而不研则退，研而不教则废”[13]．开展“SEC”模式的一致性研究，通过比较不同因素一致性的同时，引导数学教师从统计技术分析的角度看待教育教学问题，其中包括课堂教学的落实，数学试题的命制、评价以及解题方法的研究等，其研究过程能够帮助教育工作者更加深刻了解学业评价（考试）与《义务课标》、教师的教与学生的学之间的关系，加深对《义务课标》的理解，有效实施基于《义务课标》的教学，从而提升教师教学的专业水平，促进教师从“经验型”向“科研型”发展，走向专业化道路．

由于仅从定量分析的角度对2013—2016年厦门市中考数学试卷与《义教课标》的一致性程度进行研究，研究结果表明其不具有统计学上显著的一致性，因此，需要对影响其不一致性的因素（比如教学问题、试卷命制问题）做进一步研究．总之，基于课程标准的中考数学试卷的一致性研究尚处于起始阶段，广大数学教育研究工作者应致力于开发出适应我国教育的一致性研究工具，扩大其研究广度（如课堂教学实录、教案、教材习题、试题命制等），进行多区域比较，开展多方位研究，注意可执行度和编码的信度问题，从统计分析的角度使教育政策的制定者更直观了解各区域的教育发展状态，使义务教育迈向优质均衡化发展，使教学的执行者能更好地执行基于标准的教学，更好地发挥出中考的导向作用，更好地促进一线教师对课程标准的理解提供相关统计数据．

[1] 中华人民共和国教育部．基础教育课程改革纲要（试行）[EB/OL]．（2011-12-06）[2017-03-10]．http://www.360doc. com/content/11/1206/19/7015966_170182949.shtml.

[2] 安淑华．中国数学教育改革的几点思考[J]．数学教育学报，2004，13（4）：10-12．

[3] 崔允漷，夏雪梅．试论基于课程标准的学生学业成就评价[J]．课程·教材·教法，2007，27（1）：13-18．

[4] NORMAN L W. Alignment of science and maths standards and assessments in four states [M]. Washington, D. C. : Council of Chief State School Officers, 1999: 23.

[5] 刘学智，马云鹏．美国“SEC”一致性分析范式的诠释与启示——基础教育中评价与课程标准一致性的视角[J].比较教育研究，2007，29（5）：64-68．

[6] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：3．

[7] 上海市教育委员会．上海市中小学数学课程标准（试行稿）[M]．上海：上海教育出版社，2004：29．

[8] 缪琳，陈清华．基于“SEC”一致性分析的初中数学考查研究[J]．上海教育科研，2017（2）：43-49．

[9] GAVIN W F. Estimating critical values for strength of alignment among curriculum, assessments, and instruction [J]. Journal of Educational and Behavioral Statistics, 2011, 36(6): 393-394.

[10] 吕世虎，江懿，李强．义务教育阶段数学新课程实施现状调查——从甘肃省教师视角的研究[J]．数学教育学报，2011，20（5）：32-36，51．

[11] 董琴，郭凌，马云鹏．基于标准的学业评价模式：瑞典数学课程评价评析[J]．数学教育学报，2016，25（3）：29-33．

[12] 骆洪才，昌国良，范凌．义务教育数学课程改革研究阶段性评述[J]．数学教育学报，2008，17（3）：23-26．

[13] 游家水．科研型教师的素质及其培养的对策[J]．教育导刊，2004（Z1）：102-104．

[14] 郑强，杨世明．科研型数学教师及其培养[J]．数学教育学报，2002，11（3）：72-74．

Analysis of Compulsory Education Curriculum Standards in Consistency with Senior High School Entrance Examinations——Based on the Mathematical Test Papers in Senior High School Entrance Examination in Xiamen (from 2013 to 2016)

MIAO Lin1, 2, CHEN Qing-hua1, SU Sheng-kui1, 3

(1. College of Mathematics and Informatics, Fujian Normal University, Fujian Fuzhou 350117, China;2. Shanghai Hongkou Experimental School, Shanghai 200080, China;3. No.6 High School of Xiamen, Fujian Xiamen 361012, China)

Analysis and research of senior high school entrance examinations, which were based on the compulsory education mathematics curriculum standards, were the novel view to explore the correlation between the designs of the country curriculum in current new reform of curriculum education and the evaluation system of mathematical achievement. This paper constructed the model of Surveys of Enacted Curriculum (SEC) and analyzed the correlation between the mathematical test papers in senior high school entrance examination in Xiamen and the compulsory education mathematics curriculum standards via taking cognitive level as the core-dimensions. Our results showed that they were not statistically significant alignment and there exists some main difference. We suggested to improve the curriculum standards, normalize the curriculum evaluation system, and further the research on different alignments. All works would be conducive to reasonably correcting the examinations and promoting the development of the teachers’ specialization.

curriculum standards; senior high school entrance examinations; alignment analysis

[责任编校：周学智]

G632.0

A

1004–9894（2017）05–0044–05

缪琳，陈清华，苏圣奎．义务教育课程标准与中考试卷一致性分析——以2013—2016年厦门市中考数学试卷为例[J]．数学教育学报，2017，26（5）：44-48．

2017–05–12

全国教育科学“十三五”规划2016年度教育部重点课题——高中生数学核心素养的策略与评价研究（DHA160364）；福建省教育厅研究生教改项目——扎实基础，深化改革，推进数学一级学科研究生大类培养模式（2015）；福建省教育科学“十三五”规划2016年度课题——基于福建全省统一命题的数学科中考研究（FJJKXB16-013）

缪琳（1979—），女，福建福安人，中学一级教师，硕士，主要从事中学数学评价研究．