对数学教学中“教思考 教体验 教表达”的认识与思考

严 虹，游泰杰，吕传汉



对数学教学中“教思考 教体验 教表达”的认识与思考

严 虹，游泰杰，吕传汉

（贵州师范大学数学科学学院，贵州贵阳 550001）

在中国全面深化课程改革的今天，培育中小学生核心素养成为课堂教学的重要目标．核心素养是学生在接受相应学段的教育过程中，逐步形成的适应个人终身发展和社会发展需要的必备品格和关键能力．研究旨在阐述数学教学在“教思考、教体验、教表达”（简称“三教”）的教育理念下，重在培养学生的数学思维、促进学生的数学领悟、强化学生的数学交流，并最终培育学生的数学核心素养；在此基础上进一步阐述了“三教”之间的逻辑关系．

数学教学；教思考；教体验；教表达

当前中国正处在经济转型升级的关键时期，创新人才培养机制、提高人才培养质量也随之进入一个十分重要和紧迫的阶段．中小学教育务必摒弃“唯考试评价”、“唯分数论”的观念，真正树立人人成才、多样化人才、终身学习、系统培养的理念；摒弃拼规模、比数量的观念，真正树立起以人才培养为中心、以适应社会需要为检验标准、以学生为本、把促进学生全面发展、健康成长作为改革的出发点和落脚点，让每个孩子都能成为有用之才的理念．要以“立德树人”为宗旨，以发展学生“核心素养”为目标，以实现课堂教学转型和建立学校课程体系为重点．

在全面深化课程改革的大背景下，在数学教育的各个阶段中，教师如何进行数学教学，进而最终达到培育学生核心素养的目标？成为当前数学课堂教学中亟待解决的重要问题．

2014年1月，贵州师范大学吕传汉教授提出：在数学教学中教思考、教体验、教表达（简称“三教”）的教育理念，尝试用“三教”引领“创设数学情境与提出数学问题”教学，进而培育学生核心素养．主张：

教思考，让学生会用数学的思维分析世界，学会“想数学”，促进学生思辨能力的培育；

教体验，让学生会用数学的眼光观察世界，学会“做数学”，获得个人学习体验；

教表达，让学生会用数学的语言表达世界，学会“说数学”，表达、交流加深思考．

最终达到培育学生数学核心素养的目的．

1 “教思考”重在培养学生的数学思维

1.1 “思考”与“思维”的概念辨析

“思考”是指“进行比较深刻、周到的思维活动”；“思维”是指“在表象、概念的基础上进行分析、综合、判断、推理等认识活动的过程．思维是人类特有的一种精神活动，是从社会实践中产生的”[1]．

教思考，旨在让学生学会“想数学”．未来高中数学教学活动要树立以发展学生数学核心素养为导向的教学意识，创设有利于学生数学核心素养发展的教学情境，启发学生思考，引导学生把握数学内容的本质．树立敢于质疑、善于思考、严谨求实的科学精神．

数学学科教学应注重培养学生的数学思维，这是数学教育的基本目标之一．“人们在学习数学和运用数学解决问题时，不断地经历直观感知、观察发现、归纳类比、空间想像、抽象概括、符号表示、运算求解、数据处理、演绎证明、反思与建构等思维过程．这些过程是数学思维能力的具体体现，有助于学生对客观事物中蕴含的数学模式进行思考和做出判断．”[2]

1.2 “教思考”能够培养学生的“数学思维”

爱因斯坦指出“独立思考是创新的基础”．苏霍姆林斯基认为“要培养自己孩子的智力，那你就得教给他思考”．强调必须通过思考获得知识．

“思考”是指“进行比较深刻、周到的思维活动”，“进行比较深入的考虑”，“进行分析、综合、推理、判断等思维活动”．从国内学术界对于“思考”的常见定义中，可以发现“思考”具有的基本特征：比较深刻的一种思维活动．

在全球范围内不少发达国家或数学教育优质国家的数学课程标准文本中均有要求学生数学地“思考”．比如：澳大利亚教育部颁发的《澳大利亚数学课程》文本[3]中，提及“课程聚焦于培养逐步复杂的数学理解、流畅、逻辑推理、分析思考和问题解决技能”．澳大利亚F-10年级数学课程由3条内容线索和4条精通程序线索交织而成．其中，“精通程度线索是理解、流畅、问题解决和推理．它们描述了内容是怎样被探索或开发的，也就是，思考和做数学”；“学生培养一种逻辑思考和行动的越来越复杂的能力，例如分析、证明、评估、解释、推理、判断、归纳的能力”；“让学生加入到关于问题的解决方案的推理和思考中，这些需要找到解决方案的策略是数学课程的核心部分”．又如，新加坡教育部公布的《初中数学教学大纲》文本[4]中，数学课程目标中包含“发展数学思考和问题解决技能，应用这些技能公式化并解决问题”．

“数学是一种模式的科学”，在数学教学中“教思考”，让学生逐渐学会“思考”，这对于培养学生的数学思维有着特殊而重要的作用，一方面，“思维”本身就蕴含在“思考”概念内涵之中；另一方面，当教师在数学课堂中有意识地引导学生“思考”数学问题中蕴含的“数学思维方式和方法”，自然能够在潜移默化中培养学生的“数学思维品质和能力”．

1.3 在数学教学中如何“教思考”

任何学习都需要思考，数学学习尤其需要思考，没有思考就没有真正的数学学习．

在数学教学中“教思考”，就是要教学生“想数学”，教学生学会“数学地思考”．所谓“数学地思考”，就是用数学的眼光观察世界、从数学的角度思考问题．教师在数学教学中，要引导学生感受数学与生活世界的联系，在“数学地思考”过程中体验到数学刻画现实问题的价值，体验到成功应用数学知识解决问题的快乐．

“在数学教学中如何教思考”，教师可以重点考虑如下问题：

（1）在教学设计中注重渗透哲学层面的数学思维方法．比如：抽象、概括、归纳、分析（发散思考）、综合（集中思考）、判断（从概念获得、问题解决及数学应用中获得），等等．

例如，数学教学应重视引导学生进行哲学层面的思考．函数概念的教学，就要让学生理解现实生活中的问题都是多变量（因素）问题，但人们为了研究的方便，采取抽象的方法（抓主要因素，忽略次要因素，采取“主要考虑”某一变量，将多变量问题变成单变量问题来近似处理）、概括的方法（不同的现象用同一个数学模型来表述）获得相关的数学模型．北师大版数学教材九年级“函数”概念，给出了引入概念的3个情境（现象）：烧开的牛奶温度随时间而变化；公园中的摩天轮座椅高度随时间而变化；汽车刹车公式中路程随着速度而变化．这里，都明确告诉学生两个变量的关系，容易给学生造成这些现象都是单变量（因素）关系的错觉．应突出“主要考虑”路程与速度、高度与时间等关系（忽略次要因素）．

（2）在课堂教学中进行数学知识和技能传授的同时，思考有关的思维方法是如何呈现的？应通过创设恰当的数学情境，引导学生通过思考“发现问题”进而“提出问题”，尝试用数学方法“分析问题”最终“解决问题”，培养学生的数学思维．

又如，重视给小学生传递数学思维方法，在小学计算教学中要突出3点：一是转化的思想；二是在计算教学中，让学生体验解决问题方法的多样性；三是让学生在体验数学与生活的联系中进而体验数学应用的广泛性．在小学数学概念教学中要突出：一让学生体验数学的抽象性；二让学生体验数学的概括性．重视学生问题意识的培养．从小学生开始，就要诱导学生，在学习中不断发现问题、提出问题、分析问题和解决问题[5]．

（3）从解题、实验、实践的反思中，逐步培养辩证的思维方法和批判能力．

在数学教学中应该特别倡导一种批判性思维方式——“反思”．看问题的角度是否最佳？分析过程的逻辑关联度如何？解决问题的情感态度是积极还是消极？反思，是元认知（反审认知）活动，是对思维过程的审查，是完整的思维过程的重要组成部分．

新加坡数学课程中提出了一个适用于从小学到A水平所有水平的数学框架，设置了教学、学习和数学评估的方向．数学问题解决是数学学习的中心．它涉及一系列情境中数学概念和技能的获得与应用，包括非常规的、开放的和现实世界中的问题．数学问题解决能力的发展依赖于5个相互关联的成分，即：概念、技能、过程、态度和元认知．其中“元认知”也即对认知的认知，是指个人对自己思维过程的认识以及控制调节过程的能力，特别是对问题解决策略的选择和使用．它包括对思维的监控，对学习过程的自我调节．该成分的核心就是“反思”的批判性思维方式．

俗话说：失败是成功之母．如果缺少反思的思辨能力，“失败是成功之母”就会成为一句空话．《论语·学而》说：“吾日三省吾身”，它不但强调反思对处事、交友、学习的重要性，而且把反思看作是人的优秀品质之一．

通过反思来处理、改善有关问题研究．在学校学习生活中，指导学生常作生活反思、学习反思，解题反思，逐渐养成反思的习惯，定能促进学生认知的发展和事业的成功．

2 “教体验”重在促进学生的数学领悟

2.1 “体验”与“领悟”的概念辨析

在此之前，首先区分一下“经验”与“体验”：经验，由实践得来的知识或技能（有直接经验与间接经验）；体验，通过实践来认识周围的事物；亲身经历[6]．体验的特征在于：具有实践、探究的过程性；强调亲身经历；具有个性化特征，是个体内化的经验．在数学课程中，“体验”则是描述过程目标的行为动词（经历、体验、探索）之一，是指“参与特定的数学活动，主动认识或验证对象的特征，获得一些经验”．

教体验，旨在让学生学会“做数学”．此处的“体验”主要是指“学习体验”．学习体验，可以理解为学生通过有目的（有引导）的学习实践活动来感受、体会、领悟周围的事物，以及由此获得相关知识、技能、情感与观念等内容的过程．

“领悟”则是指“领会；理解”[1]．数学学习中的“数学领悟”，通常是指一种心理状态，即“新的数学概念和知识还没有被学生掌握之前，已潜伏于所展示的数学素材之中，当学生脑中已掌握的知识技能和思想方法被适时地激活后，通过持续的观察、比较、分析和判断，大胆的尝试、联想、想象和猜想，使得认识由此及彼、由表及里地不断积聚、不断深化，最终出现的恍然大悟或是豁然开朗的心理状态”[7]．

2.2 “教体验”能够促进学生的“数学领悟”

学习体验，离不开学生自己的学习活动；学习体验，是学生在活动经验基础上的反思、领悟与升华，是学生个体内化的经验；学习体验，是以学科学习的知识、技能、学科思想方法和情感、态度、价值观为载体，并通过学生个体的思考、领悟获得的思维积淀．学生这种个性化的经验积淀到一定程度后，就会积聚深化为自己独特的“数学领悟”，使得自身能够迅速理解数学知识，逐步掌握数学思维方法，最终形成自己的数学素养．

比如，数学教师通过在课堂上“教体验”，使得学生能在情境中抽象出数学概念、命题、方法和体系，积累从具体到抽象的活动经验，从而“体验”数学抽象的过程，促进自身对于“数学抽象”素养的领悟．

又如，通过在课堂上“教体验”，使得学生能感悟数学与现实之间的关联，学会用数学模型解决实际问题，积累数学实践的经验，从而“体验”数学建模的过程，进而促进自身对于“数学建模”素养的领悟．

再如，通过在课堂上“教体验”，使得学生在具体的情境中感悟事物的本质，形成数学直觉，从而“体验”直观想象的过程，进而促进自身对于“直观想象”素养的领悟．

综上所述，在数学课堂中通过教师有意识有引导地教学生“体验”，能够使得学生深化所掌握的有关表层知识，进而对蕴涵于其中的知识与技能、数学思想方法、情感与观念等内容有所感悟和体会．

2.3 在数学教学中如何“教体验”

在中小学数学课堂教学中，教师应该重点考虑如下问题：

（1）引导学生关注知识内涵与逻辑脉络的学习，重视激发学生的学习兴趣．

（2）指导学生获得数学学习体验的方法，教学生在知识理解、语言文字运用、解题、实验、实践的反思中体验有关思想方法．

（3）创设恰当的学习情境，给学生搭建体验的平台，引导学生在探究过程中获得知识、再发现的学习体验．

（4）引导学生在自主学习、合作探究、讨论辩论中获得勤于思考、敢于质疑、勇于创新的体验．

（5）获得数学活动体验，最重要的是积累提出问题和解决问题的体验，总之，是“从头”想问题、思考问题、解决问题全过程的体验．不仅仅是实践的经验，也不仅仅是解题的经验，更加重要的是思维的体验．

在数学教学中，教师要善于利用学生乐于参与的心理，在课堂上充分设置数学探究、数学实验等环节，同时在课外布置具有实践性的数学问题，引导学生真正的“做数学”，在“做数学”中学数学，并获得对数学精神、思想与方法的感悟，获得数学学习的情感体验．

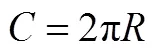
让学生获得体验：

如何从已知圆周长、圆面积的整体出发，用分成1/360等分来探求未知的弧长、面积公式．从而获得由整体探求局部的学习体验．若将弧长分为等分，每一份长为，又如何求曲边微小三角形的面积的体验？如何据此求出扇形的面积体验？（这里，也可作为一个问题留给学生走出课堂思考．）特别让学生获得足够大时，微小扇形中弧与弦曲直不分的体验——微分与求和的学习体验．从而获得由局部探求整体的学习体验．

这样，学生获得的就不仅仅是学习弧长与扇形面积公式知识的体验，重要的是获得在教师引导下的独立思考，进一步获得“由整体探求局部”和“由局部探求整体”及微分情况下的“直曲不分”辩证思维的数学领悟．

总而言之，学生学习重在学习体验的积累．这种体验的积累，就铸成学生的素养，即积淀在学生身上的终身受益的潜在能力．重视数学学习活动体验教学，有利于培养学生从该数学的角度思考问题，积累发现问题、提出问题、分析问题、解决问题的经验，促进学生具有个性特征的思辨能力的发展[5，8]．

3 “教表达”重在强化学生的数学交流

3.1 “表达”与“交流”的概念辨析

“表达”是指“表示（思想、感情）”[1]．“教表达”，旨在让学生学会“说数学”．教表达，要重视数学中“自然语言”、“符号语言”、“图形语言”的转换．

“交流”则是指“彼此把自己的供给对方”[1]．这里的“数学交流”主要是指：在课堂或课外学习过程中，能够将自己习得并理解的数学知识、技能、思想方法、情感态度等以口头或书面的形式传递给对方．

3.2 “教表达”能够促进学生的“数学交流”

苏霍姆林斯基认为：“怎样才能做到使教师与学生的关系中充满着高尚意念呢？首先必须使教师在传授给学生意识的那些思想中能表现他自己，能触及孩子心灵的不是冷冰冰的真理，而是教师活生生的、热情的个性．这要看教师传授给学生的那些知识在多大程度上已成为他自己的信念，在多大程度上进入了他的心灵．”[9]

表达是一种十分重要的软能力，引导儿童学会表达，让儿童在生生互动、师生互动中思维碰闯，在表达中倾听，在倾听中交流，在交流中思考，促进儿童知识学习的加深理解，增长智慧，获得体验，积淀素养．

表达能力是核心，表达包括书面的文字表达和口语表达．倾听他人首先基于他人表达，经过倾听者的思考后才会有各自见解的交流．学生在学科的学习活动中，通过独立思考、展示交流、质疑批判，有助于学生交流能力的培养，铸成学生终身受益的素养[8，10-20]．

3.3 在课堂教学中如何“教表达”

教学中，教师应该重视引导学生“说数学”，让学生会用数学的语言表达世界，要特别重视引导儿童进行自然语言、图形语言和符号语言的转换表达，鼓励他们敢讲话，敢追问，把自己的思考说出来，用自己原生态的、甚至有些粗糙的语言诠释对数学意义的理解，在相互表达、交流中增强学习体验．

在中小学数学课堂教学中，教师应该深入思考如下问题：

（1）引导学生在解题、实验、实践的反思中，通过师生互动、生生互动表述自己的思考．

（2）引导学生在合作学习、展示交流、讨论辩论中提升口头表达能力．

（3）指导、鼓励学生撰写“学习日记”、“学习心得”、“小论文”等，简要讲述自己感兴趣的见闻，敢于发表自己的意见，培养学生的文字表达能力．

（4）课堂结束时，布置课外作业的同时，最好能够布置一个相关的思考问题——尤其是学生讨论中出现的富于思考的问题，让学生走出课堂思考．

……

例如，2016年9月，贵州省兴义八中阳光书院尹慧梅老师在讲授“垂直于弦的直径”时，十分关注学生表达交流．她设计了4个问题的“问题串”，引导学生通过交流表达，巩固和应用垂径定理及其推论．为激活学生的思考，问题教师没有直接给出，而是在课件中以让学生以“点击”的方式随机选题回答．学生跃跃欲试，课堂气氛达到高潮．

点击出的其中一个问题如下：

问题：如图所示，⊙的直径为10，弦=8，为上的一个动点，那么长的取值范围是多少？

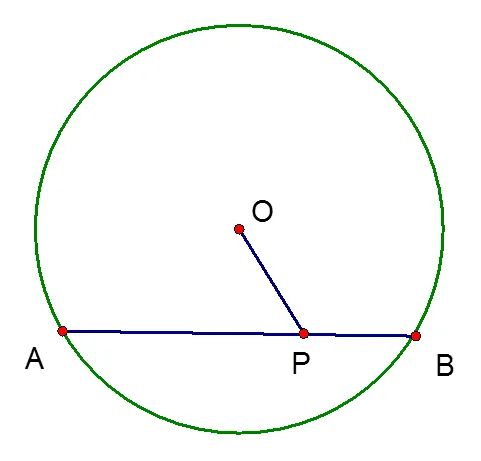
学生思考1分钟后陆续有人举手，2分钟后，举手学生达到半数．教师叫了中等成绩的学生A回答．

生A：此题要求线段的取值范围，一般应找到它的最大值和最小值，前面学过圆中最长的线段是直径，所以当点运动到或时最长为5，那么最短在哪里呢？

（因为平时的教学习惯，她当起了小老师，点名让另一个学生回答）

生B：当垂直于时最短，因为垂线段最短，但我不会求．

生C：用刚才的垂径定理，垂直于弦的直径则平分弦可知此时为的中点，再用勾股定理即可求出3≤≤5．

生D：小结一下，本题主要应用了垂径定理、勾股定理、垂线段最短这几个定理．

生E（小声的说）：还有圆的对称性．（老师给予肯定）

下课时，教师还留下一个问题让学生离开课堂思考：如何四等分一段圆弧？让学生根据课堂所学知识课后进行拓展思考、交流表达，利于促进学生核心素养的培养．

4 “三教”之间的逻辑关系

“三教”是对课堂教学本质属性的高度概括，是一个有机的整体，没有截然的界限．3者各司其职又相互配合，共同实现对学生全面发展的培养．同时，3者之间又存在着一定的逻辑关系，可以简单地概括为：

没有思考就没有体验，没有体验就难以表达，表达是思考和体验的结果；

在思考中体验，在体验中思考，因有所思考和体验而更准确的表达；

在体验和表达中产生新的思考．

具体如下：

深入思考是获得深刻体验的基础．没有深入的思考，就难以真正理解问题，就无法认识学习对象的本质，就感悟不到学科的精神和思想方法，也无法获得知识发现、科学研究中的情感体验．

深刻体验是清楚表达的前提．有所体验是言之有物的基础，正如俗语所言：如人饮水，冷暖自知．对于一个事物没有完整的、深刻的体验，要想通过语言、文字加以说明和解释，其结果就是盲人摸象、管中窥豹．

因此，在教学中，教师应通过“教思考”引导学生获得“体验”，通过“教思考”达到“教体验”，并让学生在有所体验的基础通过充分的反思、讨论、交流、辩论、倾听、叙述、描写等，发展他们的语言表达能力、文字表达能力和社会交往能力，实现“教表达”．更进一步，在体验、表达的过程中，引导学生发现新的问题，引起学生新的思考．因此，“教思考”、“教体验”、“教表达”3者之间形成一种互为基础、相互依存的关系．

5 结束语

当前，中国基础教育课程改革正处于以“立德树人”为宗旨，以发展学生“核心素养”为目标，以实现课堂教学转型为重点的“再出发”阶段，“三教”教育理念的提出，旨在培育学生的思辨能力，并在“做数学”、“说数学”中积淀学生个性化经验，促进学生数学核心素养的形成．

“创设数学情境与提出数学问题”的教学模式（简称“情境—问题”教学模式），是由贵州师范大学吕传汉、汪秉彝两位教授在2000年提出，并在西南地区乃至全国进行了长达15年教学实验研究的一种课堂教学模式．该教学模式的核心在于把“质疑提问”、培养学生的问题意识、提高学生提出问题与解决问题的能力贯穿于教学过程的始终．旨在培育学生的数学核心素养，促进创新人才的成长．

因此，“三教”教育理念与“情境—问题”教学模式，对学生的培育：

宗旨一致——培育创新型人才；

内涵一致——突出思维能力训练；

逻辑相容——以“问题”激活思考；

切入点同——从“情境”中提出问题、促进思考，解决问题；从“表达”中促进深入思考．

据此，拟在中小学数学课堂教学中，用“三教”教育理念引领“情境—问题”教学，进行培育学生核心素养的实践和理论层面的研究．

贵州师范大学基础教育师资培训中心和数学科学学院，自2015年以来，已经组织中小学专家团队，在贵州省的黔西县四中、兴义八中、兴义黄草中心学校、贵阳市、遵义市的部分中小学及习水县城乡百余所中小学，开展“三教”+“情境—问题”课堂教学培育学生核心素养的教学研究，力图通过实践层面的实证研究，探究“三教”+“情境—问题”教学的内在联系和培育学生核心素养有效的、可操作的经验．

“三教”引领数学课堂教学实验刚刚开始，尚有许多问题值得进一步思考，诸如：

（1）如何诠释“三教”理念与“情境—问题”教学模式的内在联系？

（2）如何评价“教思考”与学生核心素养培育的关系？

（3）如何引导学生在学习体验中积淀核心素养？

（4）如何引导学生在学习交流中促进思维发展？

（5）如何设计课时核心问题激活课堂学习？

（6）如何指导学生在自主学习中表达、交流与思考？

（7）如何在“情境学习”中培育学生核心素养？

（8）如何应用民族数学文化促进数学课堂学习？

（9）如何引导学生在自然语言、图形语言和符号语言转换中促进数学思维发展？

……

这些都是值得进一步研究的问题．

在全面深化课程改革的今天，要通过数学课堂教学，在“教思考、教体验、教表达”的教与学活动中，关注学生的学习活动及学习的获得．将培育学生的必备品格和关键能力的要求贯穿到各学段，融合到各学科，落实到教育、教学的全过程，最后体现在学生身上，促进中小学学生健康、良好的发展．

[1] 中国社会科学院语言研究所词典编辑室．现代汉语词典[M]．6版．北京：商务印书馆，2012：86，646，828，1 230．

[2] 中华人民共和国教育部．普通高中数学课程标准（实验）[M]．北京：人民教育出版社，2003：3．

[3] ACARA. The australian curriculum: mathematics [EB/OL]. (2014-01-01) [2017-02-08]. http://www.australian curriculum.edu.au/.

[4] Singapore examinations and assessment board. Mathematics syllabus [EB/OL]. (2013-01-01) [2017-02-08]. https:// www.seab.gov.sg/.

[5] 吕传汉，汪秉彝．论中小学“数学情境与提出问题”的数学学习[J]．数学教育学报，2001，10（4）：9-14．

[6] 夏征农，陈至立．辞海普及本[M]．6版．上海：上海辞书出版社，2010：3 867．

[7] 周建峰．数学领悟能力及其培养[J]．中学教研（数学），2005（7）：28-30．

[8] 吕传汉，汪秉彝．再论中小学“数学情境与提出问题”的数学学习[J]．数学教育学报，2002，11（4）：72-76．

[9] 王天一．苏霍姆林斯基教育理论体系[M]．北京：人民教育出版社，2003：27．

[10] 任旭，夏小刚．问题情境的创设：基于思维发展的理解[J]．数学教育学报，2017，26（4）：15-18．

[11] 陈志辉．中美两国初中数学课程的问题情境水平比较研究——以“函数”内容为例[J]．数学教育学报，2016，25（1）：5-9．

[12] 吴琼，高夯，韩继伟．高中数学教师专业知识研究——基于吉林省数学教师的调查[J]．数学教育学报，2016，25（6）：20-22．

[13] 黄友初．教师课堂教学行为的四个要素[J]．数学教育学报，2016，25（1）：72-74．

[14] 张波．两种教学方式的碰撞——在MSU和B老师一起备课[J]．数学教育学报，2016，25（1）：75-79．

[15] 韩继伟，黄毅英，林智中．初中数学教师的学科知识研究[J]．数学教育学报，2016，25（2）：49-54．

[16] 高红志，陈雪梅．思维视角下数学教师专业发展的探索——基于四节同课异构课“正弦定理”的课堂教学案例分析[J]．数学教育学报，2016，25（2）：66-68．

[17] 吕宝珠．中学数学教师对数学和科学课程整合态度的调查——以优质中学为例[J]．数学教育学报，2016，25（3）：61-65．

[18] 尹瑶芳，孔企平．国内中小学教师MPCK来源研究的定性元分析[J]．数学教育学报，2016，25（5）：22-24．

[19] 李兴贵，王新民．数学归纳推理的基本内涵及认知过程分析[J]．数学教育学报，2016，25（1）：89-91．

[20] 王立东，郭衎，孟梦．认知诊断理论在数学教育评价中的应用[J]．数学教育学报，2016，25（6）：15-17．

Cognition and Thinking about “Teaching Thinking, Teaching Experience, and Teaching Expression” in Mathematical Education

YAN Hong, YOU Tai-jie , LV Chuan-han

(School of Mathematical Science, Guizhou Normal University, Guizhou Guiyang 550001, China)

On the background of deepening curriculum reform in China, cultivation of key competence had become a very important aim in classroom teaching of primary and middle school students. Key competence was the essential character and key abilities gradually shaped adjusting to personal lifelong development and social development during the educational process for every relevant schooling section. The study was aimed at elaborating the conception that mathematical teaching should follow educational philosophy about “teaching thinking, teaching experience and teaching expression”. And based on “three teachings”, the students should develop their mathematical thinking, promote mathematical comprehension and strengthen mathematical communication. The paper further expressed the logical relationship about “three teachings”.

mathematical teaching; teaching thinking; teaching experience; teaching expression

[责任编校：周学智]

G420

A

1004–9894（2017）05–0026–05

严虹，游泰杰，吕传汉．对数学教学中“教思考 教体验 教表达”的认识与思考[J]．数学教育学报，2017，26（5）：26-30．

2017–09–03

2015年度教育部人文社会科学研究项目——基于连贯性视阈的基础教育阶段数学课程国际比较研究（15YJC880104）；天津市教育科学“十三五”规划课题——“幼小”“小初”学段衔接的课程建设实践研究（BE3330）

严虹（1980—），女，江苏南京人，教授，博士，主要从事数学教育、数学课程国际比较研究．