ICME-13之HPM专题研究综述

沈中宇，邹佳晨，汪晓勤



ICME-13之HPM专题研究综述

沈中宇1，邹佳晨2，汪晓勤2

（1．华东师范大学数学系，上海 200241；2．华东师范大学教师教育学院，上海 200062）

第13届国际数学教育大会的TSG 25是HPM研究组．此研究组一共有38个报告，报告的主题可以分为7类．从中可总结出国际HPM研究的特点有：重视理论基础；研究方法规范；多元文化交融．对中国HPM研究的启示有：构建理论框架，重视本土特色；规范研究方法，注重实证研究；关注多元文化，加强国际交流；丰富教学方式，开拓第二课堂．

ICME-13；HPM；特点；启示

国际数学教育大会（简称ICME）是国际数学教育委员会（简称ICMI）最重要的活动之一，每4年召开一次，第13届国际数学教育大会（简称ICME-13）于2016年7月24—31日在德国汉堡的汉堡大学和汉堡会议中心举行．会议共有54个专题研究组（Topic Study Group，简称TSG），其中TSG 25的主题是“数学史在数学教育中的作用”，即通常所说的HPM（History and Pedagogy of Mathematics）．

HPM专题研究组在ICME中有着较长的历史，在1976年德国卡尔斯鲁厄举行的ICME-3中，根据提议，ICMI执行委员会在它随后的会议中开设了这一研究小组[1]．而在中国，自从2005年第一届全国数学史与数学教育研讨会召开以后，数学史在数学教育中的作用日益受到关注．据统计，《数学教育学报》2010年后载文下载频次前20的论文中，就有6篇与数学史、数学文化对数学教育的作用有关[2]．虽然国内的HPM研究文献日益增多，但研究水平仍有待提高；研究者需要有国际视野，及时了解国际HPM研究动态，从中汲取经验与启示[3]．

有鉴于此，这里对TSG 25的所有报告内容进行综述和分析，试图回答以下问题：TSG 25的报告涉及哪些研究内容？有何特点？对HPM研究与HPM视角下的数学教学实践有何启示？

1 TSG 25基本情况概述

1.1 TSG 25的目标和理念

TSG 25的目标在于建立一个学术论坛，让来自世界各地的研究者分享他们的研究兴趣、研究结果和国际化的思想，包括数学史融入数学教学的理论探讨、实践经验和实证研究，并让他们从交流和研讨中获得丰厚的回报；同时，也激发年轻学者对HPM领域的研究兴趣．TSG 25的讨论包括所有层次的教育，从小学到大学，包括在职教师的培训．

TSG 25的理念是：数学是人类智慧的宝库，有着漫长的历史与充满活力的今天，因此，数学知识不仅由其演绎结构所决定，也受到原始动机的引导，这对数学知识的理解是不可或缺的．学习数学并不仅仅意味着学习现成的数学知识，还需要了解知识背后潜在的动机、数学家的活动与反思过程．因此，在数学教学中，教师需要给予学生“做数学”的机会．获取数学知识的逻辑结构和了解知识的产生过程都应该是数学教学的核心．

因此，在数学教育中，认识到数学具有以下的特征是非常重要的：不同的文化都对数学的发展做出过贡献；数学与其他科学、哲学、艺术和技术都有着密切的联系；随着时间的推移，关于“数学是什么”，已经产生过很多不同的观点；数学是刺激和支持科学技术、艺术和社会发展的永恒力量．

数学史融入数学教育有助于在学生中建立科学与人文的联系，这对今日数学教育尤为重要．通过数学学习，学生既要获得技术知识，也要接受博雅教育．

1.2 TSG 25的主题

TSG 25围绕以下6个主题展开：（1）数学史融入数学教育的理论或概念框架；（2）历史与认识论在数学教育中的应用：课堂实验和教学材料；（3）数学课程或教科书中的数学史调查；（4）课堂上的原始素材及其教学效果；（5）在数学教学中将历史和认识论作为一个跨学科的方法来揭示数学和科学的密切联系；（6）文化和数学的交融．

2 TSG 25的内容简述与分析

在TSG 25中，来自17个国家的学者共作了34个报告，其中16个为常规报告、18个为口头交流报告，另外还有4份海报．常规报告的时间为15分钟，外加5分钟讨论；口头报告的时间为10分钟，外加5分钟讨论．海报则在所有TSG的海报环节展示．

这些报告均符合TSG 25的6个主题中一个或多个主题，为了更清晰地展示各报告的内容，将其重新分成以下7类[4-6]，这7类涵盖了会议的6个主题且每个报告均属于这7类中的1类．

第1类：HPM理论探讨；

第2类：教育取向的数学史研究；

第3类：历史相似性实证研究；

第4类：教学实践与课例开发；

第5类：HPM与教师专业发展；

第6类：数学史融入数学教材研究；

第7类：技术与HPM．

图1给出了各类主题的分布．

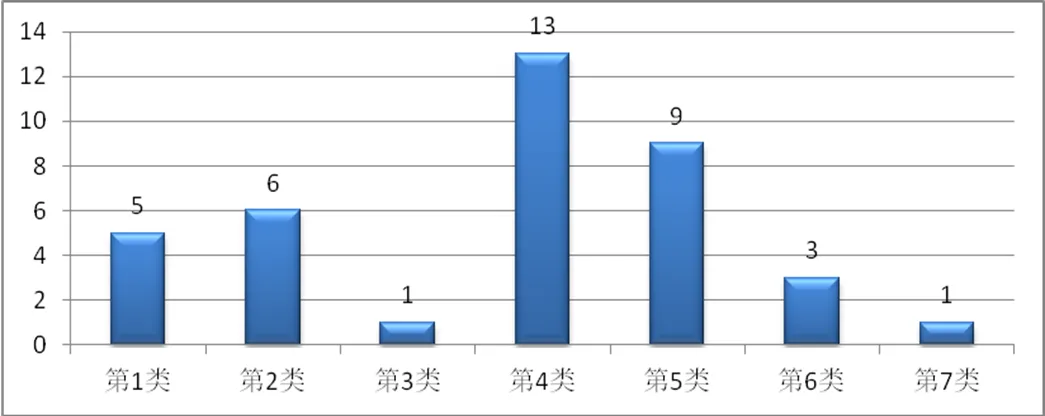
图1 38个报告中各类主题的频数分布

从图1可见，有关教学实践与课例开发、HPM与教师专业发展和教育取向的数学史研究的报告占了73.7%．

2.1 HPM理论探讨

在HPM的理论层面，需要解决“为何”与“如何”问题，即数学史的教育价值、数学史与数学教育方方面面的关联以及数学史在数学教学中的运用方式．有3个常规报告和两个口头报告聚焦理论探讨．

来自德国的Weiss-Pydstrygach在报告中指出，数学史有助于再现代数概念的几何背景，弥补代数教学中的背景缺失．报告呈现了霍纳法的丰富几何背景，说明这些几何背景可以促进和完善学生对数学的理解[7]．

来自墨西哥的Fonseca在报告中追溯了1980年代在墨西哥数学教育界兴起的社会认识论．该理论强调，数学知识是由社会建构而不是由学校创造的，学校系统中的数学知识改变了数学的结构和表现形式；数学知识的社会建构是一个从个体对数学对象的直接行动开始到人类的社会活动、到社会中的反复实践、再到作为材料和思想形态的呈现、最后到社会实践的管理这一嵌套的过程．社会认识论关注知识的4个维度——社会与文化、认识论、认知和教学，将知识视为一个动态发展的过程[8]．该理论为HPM理论与实践研究提供了参考．

来自丹麦的Kjeldsen和Johansen在报告中以卡丹（Cardano，1501—1576）的数学问题以及幂的现代理论说明，代数符号作为一种认知工具，对于学生的数学学习具有重要作用．作者建议，可以通过列出清晰的学习目标、设计学习单进行相关主题的教学[9]．

来自丹麦的Sørensen在报告中鉴于教师选择和运用数学史料的困难，提出了一个史料选择和开发的框架——从篇幅、语言和层次3个角度选择历史素材，根据教学目标将数学史作为背景或内容的支持[10]．作者又提出基于课程的数学史开发流程——从原始材料到丹麦语翻译、再到情境化、润饰和评论，最后给出教学建议．

洪燕君以三角形内角和定理的教学为例，呈现了数学史融入数学教学的实践模式——高校HPM研究团队与中学一线教师开展合作，以及具体流程——按准备、设计、实施和评价4个步骤实施教学[11]．

5个报告分别讨论数学史的教育价值、社会认识论与HPM之间联系、教育取向的数学史料的开发流程以及数学史融入数学教学的实施方法．

2.2 教育取向的数学史研究

教育取向的数学史研究是以服务教育为目的，针对数学课程中涉及的概念、公式、定理、问题的历史所进行的文献研究．该主题有一个常规报告、3个口头报告和两份海报，内容涵盖小学、中学、大学3个学段．

来自墨西哥的Vásquez鉴于学生学习加减法存在的困难，强调教学活动背后的现实与文化背景的重要性，因此对历史上的加减算法进行了考察[12]．马来西亚的Aisah在海报中鉴于学生认识负数存在困难，对负数在东西方被人们接受的历史过程作了探讨，并揭示了文化对数学发展的影响[13]．

来自德国的Sternemann在报告中对e的历史进行了研究，发现雅各·伯努利（Jacob Bernoulli，1654—1705）并没有像人们通常认为的那样发现了e，50年后的欧拉（L. Euler，1707—1783）才发现了该常数，教师可以从历史素材中获得教学启示[14]．突尼斯的Mrabet在报告中讨论了泰勒斯定理的历史，并提出若干教学建议[15]．印度的Arora在海报中考察了印度《绳法经》中的有关材料及其教育价值[16]．

来自美国的Lodder的报告考察了“网络图和生成树”的历史，并从作为工具的数学史、认知迷惑、目标层次与元层次4个方面对史料的运用进行了分析[17]．

2.3 历史相似性研究

历史相似性研究，是指根据历史发生原理，将学生对数学概念的理解过程与数学概念的历史发展过程相对照．只有一个常规报告聚焦历史相似性的实证研究．西班牙的Sanz首先考察了历史上有关分数的文字题以及不同时空数学家（如斐波那契（Fibonacci，1175—1250）、Aurel、欧拉等）的解法．让学生解同样的问题，作者发现：学生偏爱代数解法而非算术解法，因而并未显示出历史相似性．不过，作者指出，历史上数学家的解法对于从算术到代数过渡阶段的教学仍然具有重要启示[18]．

从上述报告可见，虽然前人对学生从算术到代数过渡的历史相似性已做过不少研究，但仍然存在进一步研究的空间．

2.4 教学实践与课例开发

教学实践与课例开发是指将数学史融入数学教学的实践探究，此主题是TSG 25的热点之一，共有6个常规报告、6个口头报告和一份海报涉及该主题，涵盖了小学、中学、大学不同学段．

来自希腊的Tsiapou选取中国数学典籍《九章算术》中的问题以及刘徽的事迹，对希腊的小学生开展相关的教学活动，教学实践表明，这些活动有助于学生数学观的改变[19]．

来自西班牙的Guevara在报告中指出，可以利用几何直观来学习代数．作者分析了刘徽《九章算术》注和花拉子米（Al-Khwarizmi，约780—850）《代数学》中的一元二次方程解法的潜在价值，并按Giardino的步骤，让学生完成有关任务．研究表明，几何直观对于学生从算术到代数的过渡具有促进作用[20]．法国的De Varent将古巴比伦数学泥版中的面积计算方法应用于10年级的课堂中，试图引发学生对现代方法进行反思，结果发现，泥版上的方法并未起到理想的教学效果，究其原因，可能与学生在泥版的阅读理解上存在困难有关[21]．希腊的Kotarinou让学生参与项目“希腊化时期的亚历山大：知识的灯塔”的研究，通过文献研读、话剧演出的方法让学生学习相关的数学知识[22]．希腊的Syriopoulos将历史叙事应用于教学，激发了学生的学习兴趣[23]．德国的Krohn将历史上的天文学问题用于11~12年级的教学，让学生经历历史上数学问题的解决过程，同时也迎合了现代教育的需要[24]．虞佳玮利用中国的《九章算术》和《海岛算经》中与数学课程内容相对应的问题，对法国某国际学校七~九年级学生进行了教学实验[25]．此外，方倩报告了数学史融入二项式定理的实践研究[26]，杨懿荔报告了HPM视角下的斜率概念的教学研究[27]，沈中宇报告了HPM视角下“全等三角形应用”的同课异构教学研究[28]．

也有学者对大学阶段的HPM教学实践展开研究．美国的Clark针对学生从中学数学向大学数学的过渡中所存在的困难而开设了一个讨论班，讲授从欧几里得（Euclid，约330BC—275BC）到希尔伯特（Hilbert，1862—1943）的数学发展历史．实践表明，数学史的教学有助于解决学生的过渡困难[29]．美国的Baggett在教学实践中以读书报告、研讨会的方式指导学生（来自不同国家）进行历史研究．经过6轮教学之后，作者针对所产生的一些问题，对历史研究活动作了一定的调整[30]．德国的Schöneburg实施了一项跨学科的课题研究，将有关缩放尺的历史材料用于教学，揭示了发明于四百多年以前的缩放尺的教育价值[31]．

从以上看到，有关小学数学教学的报告关注学生的信念以及原始素材的使用；有关中学数学教学的报告关注数学史在改善教学方面的有效性，并呈现了丰富多彩的实践方式．

2.5 HPM与教师专业发展

HPM与教师专业发展是关于数学史对数学教师专业发展影响的研究，在该主题上有4个常规报告与5个口头报告，涉及职前与在职两类教师．

来自加拿大的Guillemette利用历史现象学的方法对6位修读数学史课程的职前教师进行研究，通过教学录像和访谈等手段，对职前教师在阅读历史素材时产生的认识论迷失现象进行了进一步的描述，从而揭示数学史对职前教师教育的作用[32]．巴西的Bernardes将数学家西尔维斯特（Sylvester，1814—1897）和凯莱（Cayley，1821—1895）的有关工作运用于矩阵和特征值的教学，以此考察数学史对职前教师的矩阵和特征值概念转变的影响[33]．德国的Spies基于Grigutsch的信念分类和Schoenfeld等人的信念系统，对职前教师的微积分信念进行了调查；通过向职前教师讲授雅各·伯努利求抛物线切线的方法，发现他们的信念发生了改变[34]．

黄友初从MKT理论出发，就勾股定理的历史，对10名职前教师进行培训，发现数学史有助于丰富和完善他们的MKT[35]．齐春燕通过对8位职前教师的调查，发现基于数学史的问题提出活动促进了教师专门内容知识（SCK）的发展[36]．德国的Thieme利用讲座的方式对职前教师进行数学史知识（包含原始材料）的培训，发现学生对数学史知识的学习存在一定的困难[37]．

来自英国的Lawrence从拉斐尔（Raphael，1483—1520）名画“雅典学院”中的数学知识出发，设计了一门在职教师培训课程，课程提升了教师学习数学的热情，并让他们获得了职业认同感[38]．新加坡的Dindyal针对学生死记微积分公式的现象，开展了将微积分的历史融入教学的两轮课例研究，共6节课．结果表明，教师获得了专业发展[39]．王科、邹佳晨利用教师专业发展的诠释学循环模型，划分了HPM驱动下的教师专业发展的4阶段，即数学史诠释学循环和数学教学诠释学循环的分离阶段、接触阶段、交叉阶段和包含阶段[40]．

从该主题的报告可见，针对职前教师的研究关注原始素材对教师情感的影响，而针对在职教师的研究关注教师的在职培训、课例研究以及教师专业发展的模型．

2.6 数学史融入教材研究

有一个常规报告、一个口头报告和一份海报涉及数学教材中的历史分析．

来自德国的Schorcht采用4个维度对德国教科书中的数学史任务（先给出一段数学史材料，然后提出数学问题）进行了分析，并对其中涉及的数学史材料进行了分类[41]．土耳其的Kirez利用有关分析框架，对土耳其第二次课程改革之后五~八年级的数学教科书进行了考察，发现其中涉及的数学史内容较为肤浅[42]．美国的Koirala考察了2010年出版的美国“州共同核心数学标准”中涉及的数学史内容，特别分析了婆什迦罗（Bhaskara，1114—1185）《莉拉沃蒂》中的有关内容[43]．

几位报告人都是基于某个特定的框架来分析教科书中的数学史内容．

2.7 技术与HPM

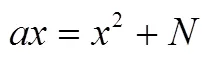
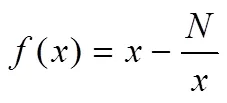
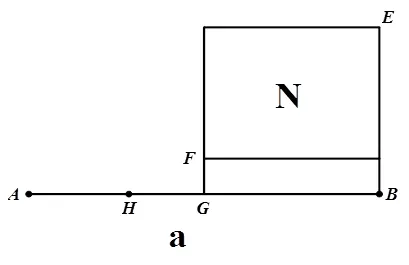
图2 解法1

图3 解法2

技术为HPM插上一双翅膀，技术与HPM的融合必将成为未来HPM研究的重要方向之一．

3 TSG 25的特点

根据TSG 25的所有报告，可以总结出当前国际HPM研究的若干特点．

3.1 重视理论基础

由38个报告可见，单纯的理论思辨、数学史研究或课堂实践较少，更多的是将数学史研究、课堂实践、教师专业发展等研究与相应的理论结合起来，重视理论的指导，这标志着HPM研究领域正在逐渐走向成熟．

报告人引用了一些常用的理论或观点．关于数学史的教育价值，有Jankvist的工具说和目标说[17]，刘柏宏对数学史教育价值的描述[39]，Heeffer和Fried等提出的数学史对数学教学的作用[23]．关于数学史的应用方式，有Sfard的认知交流理论[33]，Barnett等关于原始素材使用方式的框架[17]．关于数学史与教师专业发展的关系，有Jahnke的“再定位”（reorientation）理论[38]，Barbin的认知迷惑理论[32]，Radford的客观化（objectification）理论[32]．

还有一些报告提出了新观点或新框架．关于教育取向的数学史研究，Sørensen[7]从教师的需要出发，提出了面向课程的数学史开发流程以及供教师阅读的数学史素材的模板，有一定的借鉴意义．关于教学实践与课例开发，Kjeldsen和Johansen[19]将认知科学中的“认知工具”概念应用于数学学习中，提出“数学认知工具”概念，并指出：数史提供了数学的认知工具．关于HPM与教师专业发展，Spies[34]对已有的教师信念系统理论，如Grigutsch的工具—系统—过程—实用信念系统、Schoenfeld的经验主义信念系统以及Burscheid和Struve的形式信念系统进行了梳理和整合，从学习动机和数学本质两个新的维度来看待教师的信念．

3.2 研究方法规范

各报告运用了各种不同的研究方法，包括现象学方法、质性分析法、人种志研究、问卷调查、访谈、测试等．如，Sanz利用数学史上的问题对学生进行测试[17]；Guillemette采用现象学方法对教师阅读数学史材料之后的生活体验进行研究[32]．

Schorcht在报告中[41]首先从教科书数学史任务中提取古今联系、数学发展、数学人物、知识目标4个维度；为了对每个数学史任务进行分类，采用Mayring提出的质性内容分析法，这是一个系统的方法，一共分为10个步骤，首先将需要分析的材料提取出来，第2步确定以上所说的4个维度，第3~4步提取出材料中的属性并进行编码，属性由4个维度刻画而来，第5~7步对例子进行描述，从而必要时对属性进行修正，第8步根据极值、理论兴趣和经验频率确定属性，第9步确定原型，第10步对原型进行详细描述，再结合Kelle和Kluge的类型构建以及数学家Ganter，Wille和Stumme的形式概念分析，最后确定德国教科书中的5类数学史任务，然后利用两个例子对其中的两类任务进行了说明，最后说明利用这些属性不仅可以分析，也可以用于编制数学史相关的任务．

3.3 多元文化交融

从小学的刘徽、加减法、分数运算、面积算法、负数，到中学的一元二次方程解法、幂的表示、微积分初步、e的历史、泰勒斯定理，再到大学的网络图和生成树、矩阵等，各报告涉及丰富多彩的数学史素材，其中有古代中国、印度、希腊、阿拉伯以及欧洲的数学史素材，充分展现了数学文化的多元性．

西方学者表现出对东方历史文化的浓厚兴趣，如Guevara在其报告中发掘刘徽和花拉子米解一元二次方程方法的潜在价值[20]．Tsiapou将中国《九章算术》中的问题以及刘徽的事迹用于教学，在“哲学卡片”活动中让学生了解汉朝的历史文化对刘徽的影响，并探究刘徽在数学上发现的背景，而在“数学树”活动中让学生将刘徽的数学成就进行整理和分类[18]．这说明，国外学者对中国数学史有较深入的研究，并乐于将其应用于课堂教学．

值得注意的是，国外数学教学中运用数学史的方式十分丰富，有学习单、数学史课程、讲座、讨论班、名画中的数学史展示、原始材料的直接使用、数学拓展课、数学建模活动、戏剧表演、数学史课程包等．国内则主要集中于将数学史融入某个具体知识点的常规课堂教学中，这在某种意义上反映了东西方数学教育制度和数学课堂文化的差异．

在2012年ICME-12的HPM小组中有16%的报告由东方学者所作[45]，而到ICME-13中，这一比例上升到了26%．因此，HPM的国际化程度日益增加，东西方的学术思想必将在交融中共同发展．

4 结论与启示

由上可见，TSG 25的报告涉及7类主题；总的说来，各报告展现了重视理论基础、研究方法规范、多元文化交融的特点．据此，得到如下启示．

（1）构建理论框架，重视本土特色．理论与实践相结合为国外学者所重视，也是今后HPM研究的趋势．HPM领域的大多数理论都是建立在作者所在国家的教育现实之上的，很多学者将数学史原始文献运用于教学实践．因此，如何将有关理论以及实践经验本土化，与中国的数学教育现实相结合，建立中国HPM理论框架，值得继续探讨．

（2）规范研究方法，注重实证研究．在HPM的初创阶段，人们主要以思辨或者纯历史研究为主，而在国内，HPM领域的思辨或经验总结类的文献至今仍然占有相当大的比重．从TSG 25的众多报告中可以看出，HPM领域今天已经发展到了实证研究阶段，因此，需要建立并采用科学合理的研究方法，提升HPM的研究水平．

（3）关注多元文化，加强国际交流．在信息化和全球化时代，多元文化在世界学术界已深入人心，传统的“西方中心论”早已成为明日黄花．而在课堂上，只讲“中国最早”、“中国第一”的数学史话题也是远远不够的．HPM本身就是一个跨学科的研究领域，要求研究者具有开阔的视野和博大的胸怀．加强中外交流、借鉴他山之石、关注多元文化、博采东西方数学史素材，是未来HPM理论和实践研究的必然需求．

（4）丰富教学方式，开拓第二课堂．国外HPM教学实践形式较为开放，主题也比较丰富．而在国内，由于升学压力和教学进度的限制，HPM在课堂上的空间很小．可以借鉴国外相关经验，通过更多样的形式（如拓展课程、数学话剧等）来运用数学史，更好地发挥数学史的育人价值，让数学史真正成为数学学科落实“立德树人”根本任务的有效教学工具．

[1] 冯振举，戴丽丽．国际HPM的发展历程及启示[J]．西北大学学报（自然科学版），2005（5）：652-656．

[2] 万家练．对《数学教育学报》下载频次较高的论文评析——以2010年后的载文为例[J]．数学教育学报，2016，25（2）：96-102．

[3] 康世刚，胡桂花．对我国“数学史与中小学数学教育”研究的现状分析与思考[J]．数学教育学报，2009，18（5）：65-68．

[4] 汪晓勤，张小明．HPM研究的内容与方法[J]．数学教育学报，2006，15（1）：16-18．

[5] 汪晓勤．HPM的若干研究与展望[J]．中学数学月刊，2012（2）：1-5．

[6] 汪晓勤．数学史与数学教育研究[C] // 鲍建生，徐斌艳．数学教育研究导引．南京：江苏教育出版社，2013：403-422．

[7] PYDSTRYGACH Y W. Algebra without context is empty, visualizations without concepts are blind [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[8] FONSECA F W R. The socioepistemologic approach to the didactic phenomenon: an example [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[9] KJELDSEN T H, JOHANSEN M W. The history of artifacts as a resource in mathematics education [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[10]  SØRENSEN H K. Facilitating source-centered history of mathematics in Danish upper-secondary mathematics education [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[11]  HONG Y. Teaching mathematics from the perspective of HPM: process and model [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[12]  VÁSQUEZ M R. History of mathematics in the classroom: algorithm of the addition and subtraction [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[13]  AISAH. How negative numbers can be accepted in the community [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[14]  STERNEMANN W. About continuous compound interest by Jacob Bernoulli [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[15]  MRABET S. The development of Thales theorem throughout history [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[16]  ARORA. Activities for the construction of geometrical figures based upon Sulba Sutra [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[17]  LODDER J. Primary historical sources in the classroom: graph theory and spanning trees [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[18]  SANZ M T. Missing curious fraction problems: the unknown heritage and the unknown numbers of heirs [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[19] TSIAPOU V. Liu hui shares his views about mathematics with students of a Greek primary school [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[20]  Guevara I. Geometry and visual reasoning to introduce algebraic language as Liu Hui and Al-Khwarizmi did [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[21]  VARENT C. Consequences of the use of an ancient mathematical tablet in the classroom [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[22]  KOTARINOU P. Expanding contexts for teaching upper secondary school geometry [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[23]  SYRIOPOULOS S. The course of a theorem in time: a mathematical narration addressed to 11th grade students. [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[24]  KROHN T. Authentic & historic astronomical data meet new media in mathematics education [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[25]  YU. Teaching mathematics in Chinois by using Chinese mathematical history [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[26]  FANG Q. Instructional design and implementation of binomial theorem from the perspective of HPM [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[27]  YANG Y. An instruction design about inclination and slope [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[28]  SHEN Z. Teaching of application of congruent triangles from the perspective of HPM [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[29]  CLARK K. A seminar designed to address the transition problem from school to university mathematics: initial results [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[30]  BAGGETT P. Involving students in research in the history of mathematics education: from book report to major project [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[31]  SCHÖNEBURG S. The pantograph----a historical drawing device for math teaching [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[32]  GUILLEMETTE D. An empirical study concerning lived experience of pre-service teachers engaged in the reading of historical texts [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[33] BERNARDES A. History of matrices: promoting commognitive conflicts and encouraging reflection on meta- discursive rules in prospective teachers [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[34]  SPIES S. Making domain-specific beliefs explicit for prospective teachers----an example of using original sources [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[35] HUANG H. A qualitative study on the development of pre-service teachers’ knowledge in the history of mathematics----a case of the Pythagorean theorem [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[36]  QI C. Research on the problem posing of the HPM [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[37] THIEME B S. A curriculum for history of mathematics in pre-service teacher education [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[38]  LAWRENCE S. Euclid’s art after Bath [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[39]  DINDYAL J. A historical perspective for teaching calculus: the development of a lesson package [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[40]  WANG K, ZOU J. The model of teachers’ professional development on integrating the history of mathematics into teaching in Shanghai [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[41]  SCHORCHT S. History of mathematics in textbooks from first to seventh grades----types of tasks [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[42]  KIREZ B. History of mathematics in the Turkish middle school mathematics curriculum and textbooks [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[43]  KOIRALA. Using history of mathematics to address the Common Core Standards [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[44]  SUZUKI T. The method of geometrical solution of equations using Geogebra: focus on the root of quadratic equations in Ars magna [C]. Hamburg: 13th International Congress on Mathematical Education, 2016.

[45] 黄友初，朱雁．HPM研究现状与趋势分析[J]．全球教育展望，2013，42（2）：116-123．

Research Summary of HPM in ICME-13

SHEN Zhong-yu1, ZOU Jia-chen2, WANG Xiao-qin2

(1. Department of Mathematics, East China Normal University, Shanghai 200241, China;2. College of Teacher Education, East China Normal University, Shanghai 200062, China)

The TSG 25 of ICME-13, held in Hamburg in July 2016, focused on the role of history in mathematics education. There were a total of 38 reports in this study group which dealed with seven types of topics. It was revealed from all reports of TSG 25 that importance was attached to theoretical basis, research methodology and multicultural communication.

ICME-13; HPM; features; enlightenment

[责任编校：周学智]

G40–03

A

1004–9894（2017）05–0071–06

沈中宇，邹佳晨，汪晓勤．ICME-13之HPM专题研究综述[J]．数学教育学报，2017，26（5）：71-76．

2017–05–14

上海市教育科学研究重大项目——中小学数学教科书的有效设计子课题——中小学数学教科书中数学文化素材的案例设计（D1508）

沈中宇（1991—），男，江苏苏州人，博士生，主要从事数学史与数学教育研究．