小学生几何直观能力测评模型的构建探究

张和平，裴昌根，宋乃庆



小学生几何直观能力测评模型的构建探究

张和平1，3，裴昌根1，2，宋乃庆1，2

（1．中国基础教育质量监测协同创新西南大学分中心，重庆 400715；2．西南大学数学与统计学院，重庆 400715；3．凯里学院，贵州凯里 556011）

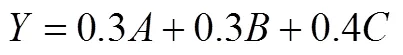
小学生；几何直观能力；测评指标；测评模型

几何直观能力是人思维能力发展的基础，是公民的重要素养，也是基本素养，对人的终身发展意义重大．几何直观是《义务教育数学课程标准（2011年版）》[1]（以下简称《标准》）中的一个核心概念，也是中国新提出的数学核心素养之一[2]．随着《标准》的颁布，学界对“几何直观能力”虽有不少研究，但主要关注其内涵[3]与课堂教学[4]方面，对学生几何直观能力的测评研究鲜有．几何直观能力测评模型是科学、客观检测学生几何直观能力的一种定量评价手段，在当前中国注重发展学生核心素养的改革背景下，构建小学生几何直观能力的测评模型显得重要而迫切．通过文献分析、实证调查等方法，借鉴学生课业负担测评模型[5]、小学低段数学符号意识测评指标体系[6]等已有测评模型研究思路，可界定几何直观能力的操作性定义，探索其测评指标，基于因子分析法和专家评分两种方法构建小学生几何直观能力的测评模型，并对模型进行初步检验．

1 相关研究

1.1 几何直观能力内涵的研究

关于几何直观能力的认识，国内外学界有不同的看法．早在1984年，徐本顺、商应钢在“关于思维中的几何直观问题”一文中提出：“借助于几何直观进行思维，不妨称它为几何直观思维．这种思维既有形象思维的特点，又有抽象思维的特点，它属于中间思维形式．”[7]中国数学家徐利治认为：“借助于见到的或想到的几何图形的形象关系产生对数量关系的直接感知，即可称为几何直观．”[8]Jones在一文中指出，“首先，几何直观在解决几何问题时起到关键决策作用；其次，直观的一些机制在解决问题的过程中的某个环节是有影响的．”[9]在2004年召开的第十届国际数学教育大会（ICME-10）上，Fujita和Jones所作的报告把几何直观（geometrical intuition）定义为，“作为在心里创建和操纵几何图形的一种技能，能看到几何特性，通过图像联系几何概念和定理，并决定从哪里开始什么时候解决几何问题．”[10]

《标准》把“几何直观”界定为：“几何直观是指利用图形描述和分析问题”[1]《标准》颁布后，几何直观能力培养引起了更多的理论研究者和实践者的重视．有学者认为：“几何直观是指，借助于见到的（或想象出来的）几何图形的形象关系，对数学的研究对象（空间形式和数量关系）进行直接感知、整体把握的能力．”[11]也有学者提出“几何直观是种意识，也是种技能与能力，更是种思维方式”[12]的多种表现形式．还有学者把几何直观能力划分为直观感知和直观洞察两个能力层次[13]．

由已有文献发现，几何直观能力主要涉及认识基本图形、直观感知、直观洞察、利用图形描述问题、利用图形分析问题、利用图形解决问题．因此，几何直观能力是指形成图形的认识并利用图形描述与分析数学问题的能力．

1.2 测评模型的研究

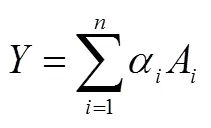
2 操作性定义及测评指标

2.1 操作性定义

基于对已有研究的分析，初步将小学生几何直观能力的行为表现划分为认识基本图形、直观感知、空间想象、直观洞察、数形结合、利用图形描述问题、利用图形分析问题、利用图形解决问题等8个方面，并藉此设计访谈提纲．

经过多次访谈与论证，调整了原有行为表现，舍去直观感知、空间想象、直观洞察、数形结合4个指标，接受教育专家与一线教师的一些意见，增加了“由具体物体抽象出图形”的行为指标，初步构建了小学生几何直观能力的操作性定义：（1）学生由具体物体抽象出图形；（2）认识图形并能用符号表示图形，会画基本的图形；（3）利用图形描述问题，主要是利用图形表示数以及运算、数学问题，把复杂问题变得简明、形象；（4）利用图形分析问题，探索解决问题的思路；（5）利用图形解决问题，通过图形建立数量关系，得出结果．这个操作性定义是探索测评指标和构建测评模型的重要支撑．

2.2 测评指标的初步探索

按照操作性定义，综合教育专家与一线教师意见，初步构设了小学生几何直观能力的测评指标，即由具体物体抽象出图形、认识图形、利用图形描述问题、利用图形分析问题、利用图形解决问题5个维度，每个维度下划分出不同的行为观测指标（观测变量）．

组织重庆、贵州两地的教育专家、一线教师和教研员，共同编制了小学生几何直观能力的测试题．试题编制的基本构想是将小学生几何直观能力划分为5个维度，每个维度预设相应的行为观测指标．在贵州抽取3所具有代表性学校四年级共122名学生进行初试，经讨论与修改，形成比较正式的测试题．该测试卷共10个题项（TM1、TM2、……、TM10），各题项具体反映的测试维度如表1所示．

表1 测试题项以及具体对应测评指标维度

正式施测，抽取贵州省3所具有代表性学校的四年级学生进行测试，共发放问卷541份，收回520份有效测试卷，有效率为96%．整套测试题的Cronbachs Alpha系数为0.624，依据已有研究成果[16]，该测验是可以接受．以10个测试题的得分作为原始数据进行探索性因子分析，Kaiser-Meyer-Olkin值是0.752，表示各题项间有共同因素存在，可以进行因子分析．用主成份分析法提取特征值大于1的因子，其旋转成份矩阵如表2所示．

由表2可知，对照原假设题项所反映的测试项目，并综合考虑各因素的共同性和在各抽取因子上的负荷量差异，得到以下结果：（1）从10个反映小学生几何直观能力的测试题中提取出3个主成份，即把预设的5个测评指标降维成3个测评指标；（2）“由具体物体抽象出图形”、“认识图形”两个指标被提取到一起，“利用图形分析问题”、“利用图形解决问题”两个指标被提取到一起．主要基于以下原因：研究认为“具体物体抽象出图形”、“认识图形”都属于学生在认识和掌握图形过程之中的一种能力表现，因此将提取的这一成份重新组合记为“形成图形的认识”，即能由具体物体抽象出图形，形成对图形及其形状的认识，并会画基本图形的能力；而对于“利用图形分析问题”、“利用图形解决问题”的合并重组，采纳了专家的意见“针对几何直观，主要体现在分析问题上，解决问题可以看成是分析问题的一个组成部分”，以及结合《标准》对“几何直观”描述性界定即“几何直观是指利用图形描述和分析问题”，因此把提取的这一成份记为“利用图形分析问题”，把“利用图形解决问题”作为“利用图形分析问题”的一个二级测评指标．事实上，反过来认真分析《标准》对“几何直观”描述性定义，发现有3个关键词（或是3个过程）：一是（掌握）图形，二是（利用图形）描述问题，三是（利用图形）分析问题，这和探索性因子分析结果不谋而合，形成相互佐证．

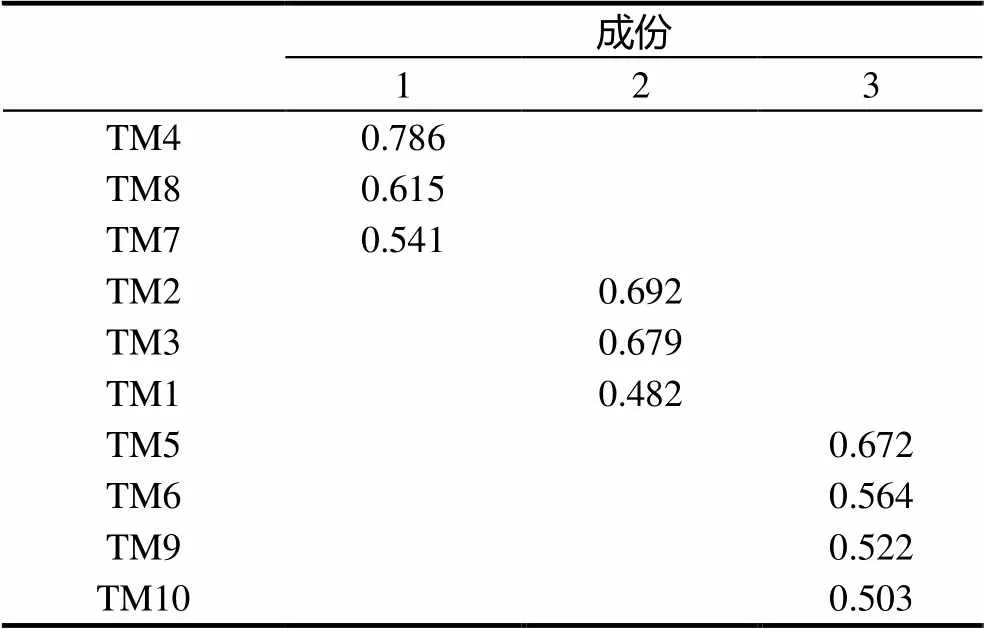
表2 旋转成份矩阵a

综上，从原构想的5个测评指标中提取并重新整合得到了3个一级测评指标，即形成图形的认识、利用图形描述问题和利用图形分析问题．基于操作性定义，并通过对专家反复的咨询，也确定了3×3个二级指标，如表3所示．

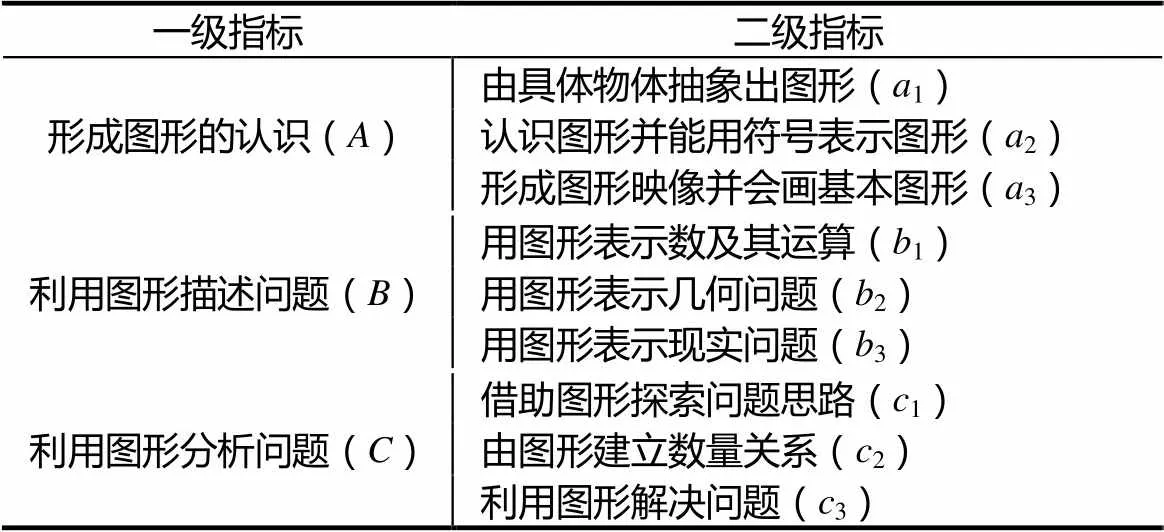
表3 小学生几何直观能力测评指标及符号表示

2.3 测评指标的认同度与验证性分析

经文献梳理和探索性因子分析提取小学生几何直观能力的测评指标，需要对指标进行验分析，主要考察高校教育专家、一线小学教师与教研员等对测评指标的认同度，以及二级指标对一级指标的解释度等．研究者将小学生几何直观能力测评指标编制成问卷，通过问卷调查收集数据进行验证性因子分析．该问卷分两个部分，第一部分是对9个二级测评指标的认同度进行评价，采用李克特5级量表记分，选项“完全同意”、“较同意”、“不清楚”、“较不同意”、“完全不同意”分别记为5分、4分、3分、2分和1分，一方面是对探索出的测评指标验证其认同度与解释度，另一方面是借助结构方程模型计算因素负荷量确定指标权重；第二部分是对3个一级指标的重要性进行评分（共为100分），旨在通过专家评分法确定测评指标的权重．然后，通过两种方法综合构建测评模型．

利用所编制的调查问卷对重庆市数学培训班学员进行初试，经修改后形成正式的问卷．正式问卷的施测对象来自重庆、贵州、海南、吉林、浙江等省（市）承办的小学数学教师国家（省）级培训班学员和培训专家，共发放调查问卷480份，回收有效问卷共431份（其中教育专家23人，小学教师与教研员403人，其他5人），有效率为90％．问卷的Cronbachs Alpha系数为0.839，调查问卷具有较高信度．

2.3.1 测评指标的认同度分析

对问卷中的9个二级指标进行了认同度分析，结果如图1所示（1:3代表的指标见表3）．

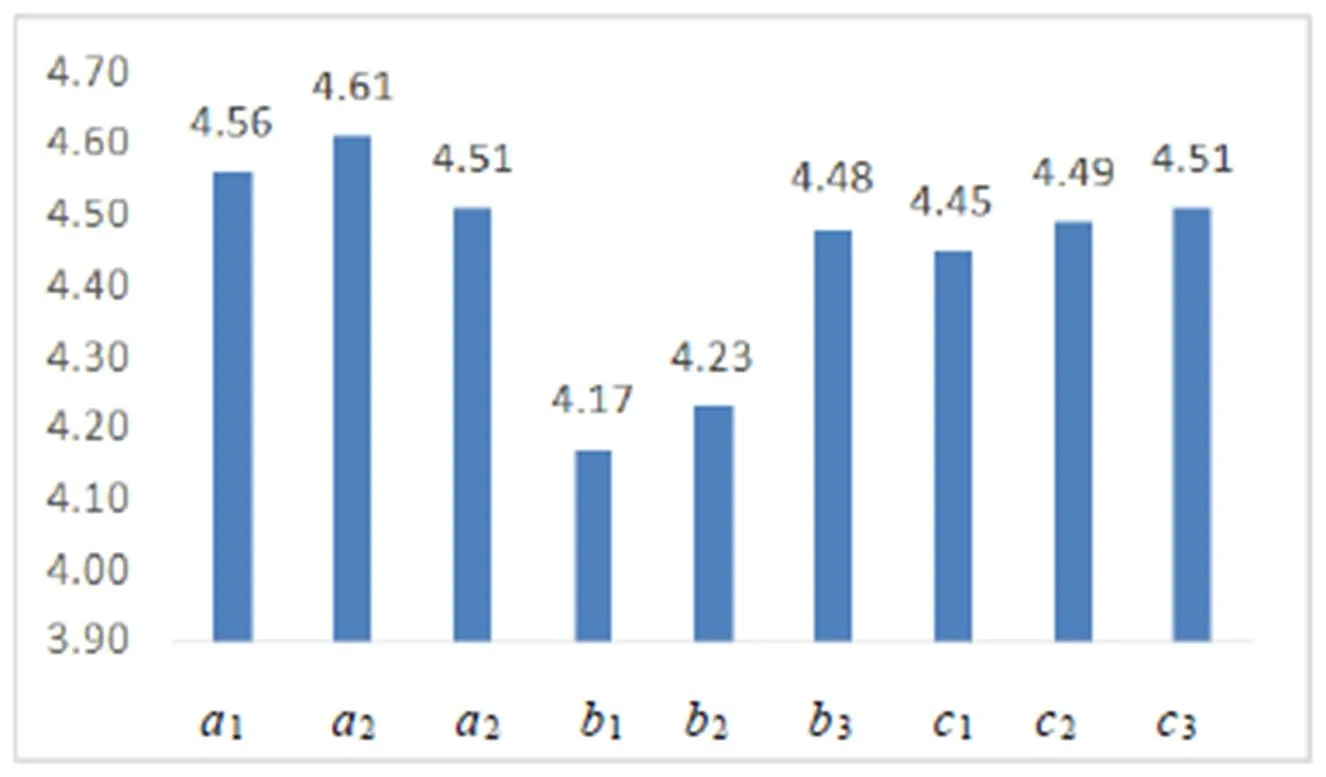
图1 测评指标的认同度调查结果

从图1看出，所有指标的认同度都比较高，达到4.17以上．不仅如此，从认同度图形变化趋势中还发现数据具有一定的规律性，即9个测评指标中前3个指标认同度均值整体最高，其次是后3个指标，中间3个指标认同度均值整体最低．从上述数据分析可知，一方面说明调查对象对“形成图形的认识”、“利用图形分析问题”的认同度高于“利用图形描述问题”，另一方面也体现了教育专家、小学教师与教研员对“用图形来表示数及其运算”（认同度为4.17）可能关注较少．

2.3.2 测评指标的验证性因子分析

利用二级测评指标调查问卷数据进行验证性因子分析（），并用AMOS24.0软件作为计算工具，结果如图2和表4所示．

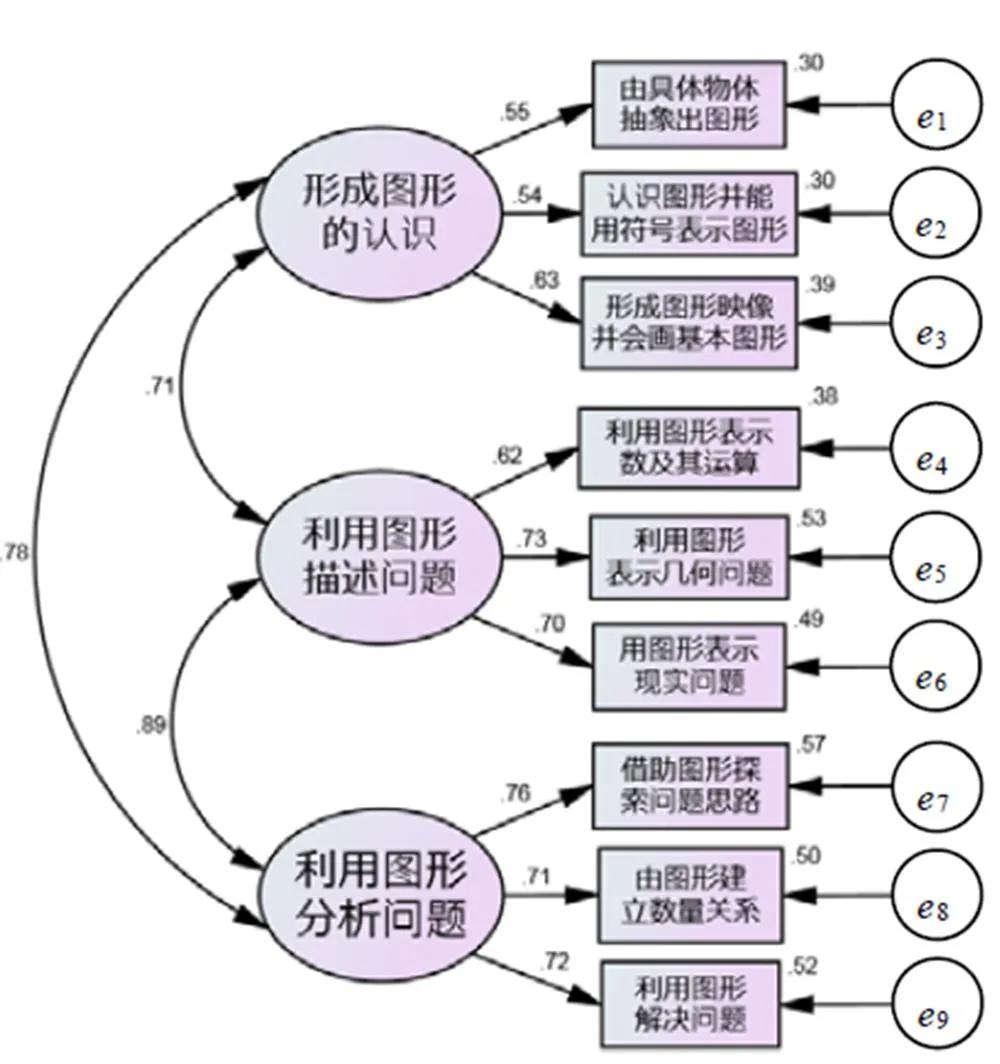
图2 验证性因子分析结果

表4 验证性因子分析适配指标结果

从图2中数据发现，因素负荷量介于0.54至0.89之间，说明模型的基本适配度良好[17]．从表4的数据结果可知，预设模型的基本适配指标均达到标准，表示样本数据与预设模型的拟合度良好，初步说明所划分的测评指标科学、合理。

3 测评模型的构建

基于前面对测评模型的相关理论分析，为保证构建测评模型的可靠性，利用因子分析法和专家评分法综合尝试构建小学生几何直观能力的测评模型．

3.1 利用因子分析法构建测评模型

在前面进行的验证性因子分析中发现，3个一级指标之间存在较高的关联度，分别是0.71、0.89、0.78，且样本数据与预设模型适配较好，说明该研究可能存在一个较高阶潜在变量可以解释这3个维度，因此进行了二阶验证性分析，结果如图3所示．

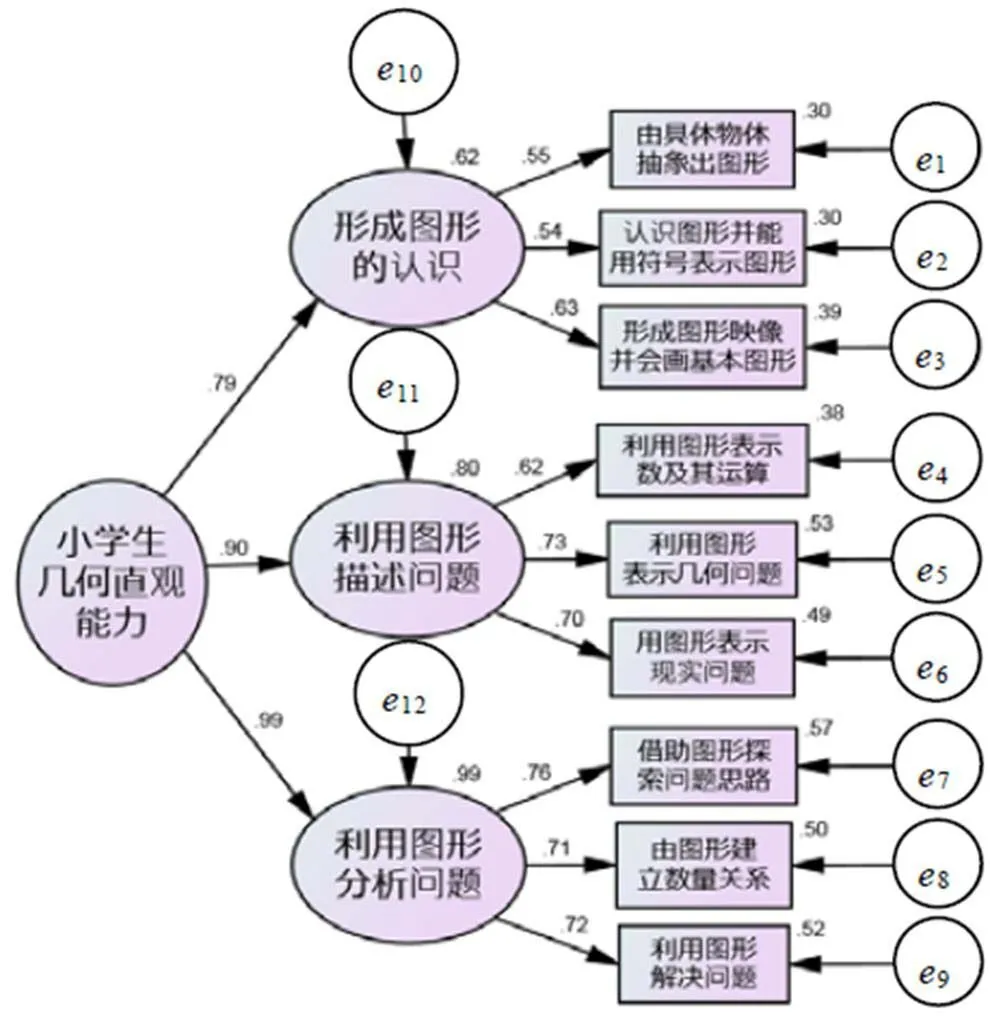
图3 验证性因子分析结构方程模型标准化系数

表5 二阶验证性分析适配指标结果

由表5数据可知，样本数据与预设模型具有良好的拟合度和适配度．由于结构方程模型的因素负荷量表示因子之间关系密切程度[18]，因素负荷量越大表示该因子越重要．因此，依据因素负荷量的大小可以确定因子的权数．借鉴已有的测评模型构建方法，利用图3中的因素负荷量值，经计算并标准化后3个一级指标“形成图形的认识”、“利用图形描述问题”、“利用图形分析问题”在几何直观能力中的重要程度比例为0.29:0.34:0.37．对二级指标进行迭代运算，并标准化，“形成图形的认识”中3个观测变量比值为0.32:0.32:0.36，“利用图形描述问题”中的观测变量比值为0.30:0.36:0.34，“利用图形分析问题”中的观测变量比值为0.35:0.32:0.33．用数学线性表达式表示，可得小学生几何直观能力测评模型为：

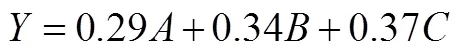
并且，

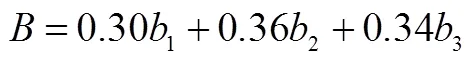
利用综合权重表示测评模型，可写为：

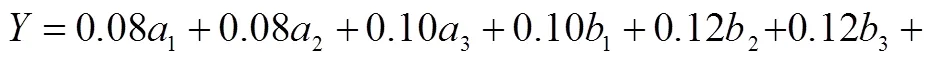
3.2 运用专家评分法构建测评模型

设计专家评分方法，旨在从中收集到更丰富的信息，而且便于对部分专家的评分进行有针对性的回访．对问卷第二部分3个指标数据求均值，结果依次是0.33、0.31、0.36．借鉴相关研究的线性描述方式，基于对模型应该好理解、好测算的原则，按照调查结果的重要程度均值构建小学生几何直观能力测评模型的数学线性表达式为：

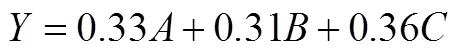
其中、、、所代表的意义与①式相同．专家评分法更表现的是质性研究，考虑到测试实际情况的需要，只要求给3个一级指标的重要程度评分．

3.3 小学生几何直观能力测评模型表述

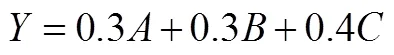
4 模型的初步检验

测评模型的构建，需要对其进行必要的检验．研究检验模型合理性的基本方法有二：一是专家对模型结构的质性判断；二是利用测评指标及其模型编制测试题并实施测试，考察模型的可操作性、可靠性与延展性．

4.1 专家判断

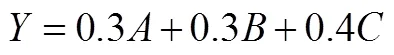
4.2 测试检验

研究构建的测评指标和模型的重要目的之一是为了编制小学生几何直观能力的测试卷，并用测试题测试分析学生的能力特征．借鉴TIMSS关于内容维度（数与代数、图形与几何、统计与概率）的比例，按照上述测评指标和测评模型编制成一套测试卷，经过组织西南大学教育专家和贵州的小学教师与教研员讨论，以及初试与修改，最后形成一套由10个题目构成的“小学生几何直观能力的测试题”．研究抽取贵州、重庆等有代表性学校的四年级、五年级、六年级学生进行测试，发放试卷1 192份，收回有效问卷1 093份，有效率92%．对试卷进行初步分析，整套测试题的Cronbachs Alpha系数为0.616，表示该测验可以接受．经计算，四、五、六年级成绩均分分别是57.41、69.03和77.84，说明测试题检测结果能反映小学生的几何直观能力会随着年级的增高而提升，经方差检验年级之间的成绩存在显著性差异（=0.00<0.05，=133.161）．因此，研究构建的小学生几何直观能力测评指标及其模型符合专家们的经验和认识，获得专家较好的认同．按照测评指标及模型编制的测试题，经检测分析，测试题能在大范围进行测试，具有可操作性，能反映小学生几何直观能力会随着年级的增高而提升的特征．

5 讨论与结论

5.1 讨论

5.1.1 几何直观能力测评指标关系及权重值的复杂性

研究是基于文献梳理、专家咨询以及《标准》的基础上经因素分析确定测评指标，提出3个一级指标和9个二级指标，并获得较高的认同度，但从文献梳理和操作性定义探索可知，几何直观能力测评涉及数与代数、图形与几何、统计与概率三大课程内容领域，确定测评指标难度很大，可能存在多种测评视角．研究在构建测评模型过程中主要考虑对象是针对整个小学，3个能力指标权重比例为3:3:4，但不同年龄段的学生各个指标的能力要求可能是存在差异的，一年级可能注重“形成图形的认识”能力培养，而六年级可能更注重培养学生“利用图形分析问题”的能力，因此，在使用测评模型过程中要根据需要适当调整．

5.1.2 利用因子分析和专家评分两种方法综合构建测评模型

研究采用因子分析法和专家评分法分别构建了两个测评模型①与②．经四舍五入取整十数后3个能力指标的系数比例都是3:3:4，一定程度上说明两种方法构建的模型基本具有一致性．因子分析法构建测评模型主要基于实证数据的分析，具有客观性；而专家评分法主要依靠专家的专业知识与经验，具有主观性，将二者结合起来，是定量研究与定性研究相结合的一种构建方法，既客观又符合实际，提高了研究结果的可靠性．

5.2 结论

研究得出如下主要结论：

（1）初步形成“小学生几何直观能力测评指标”，包括3个一级指标和9个二级指标．

（3）经检验，该测评模型可操作，数据结果与专家判断基本一致．

总之，该模型是测评小学生几何直观能力科学、可靠且可操作的工具．

[1] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：6．

[2] 洪燕君，周九诗，王尚志，等．《普通高中数学课程标准（修订稿）》的意见征询——访谈张奠宙先生[J]．数学教育学报，2015，24（3）：35-39．

[3] 朱黎生．《义务教育数学课程标准（2011年版）》修订了什么[J]．数学教育学报，2012，21（3）：7-10．

[4] 蒋文蔚．几何直观思维在科学研究及数学教学中的作用[J]．数学教育学报，1997，6（4）：67-71．

[5] 宋乃庆，杨欣，王定华，等．学生课业负担测评模型的构建研究——以义务教育阶段学生为例[J]．西南大学学报（社会科学版），2015，41（3）：75-81．

[6] 李艳琴，宋乃庆．小学低段数学符号意识测评指标体系的初步构建[J]．课程·教材·教法，2016，36（4）：23-28，38．

[7] 徐本顺，商应钢．关于思维中的几何直观问题[J]．西北大学学报（自然科学版），1984（2）：91-96，105．

[8] 徐利治．谈谈我的一些数学治学经验[J]．数学通报，2000，39（5）：1-3．

[9] JONES K. Researching geometrical intuition [J]. Proceedings of the British Society for Research into Learning Mathematics, 1993, 13(3): 15-19.

[10]  FUJITA T, JONES K, YAMAMOTO S. Geometrical intuition and the learning and teaching of geometry [C]. Copenhagen: The 10th International Congress on Mathematical Education (ICME-10), 2004: 2-3.

[11] 孔凡哲，史宁中．关于几何直观的含义与表现形式——对《义务教育数学课程标准（2011年版）》的一点认识[J]．课程·教材·教法，2012，32（7）：92-97．

[12] 蔡宏圣．几何直观：小学数学教学的视角[J]．课程·教材·教法，2013，33（5）：109-115．

[13] 曹培英．跨越断层，走出误区：“数学课程标准”核心词的实践解读之四——几何直观（上）[J]．小学数学教师，2013（6）：12-15．

[14] 蔡庆有，邝孔秀，宋乃庆．小学数学教材难度模型研究[J]．教育学报，2013，9（5）：97-105．

[15] 朱亚丽．义务教育资源配置均衡发展测评模型的构建研究——基于对重庆统筹城乡教育的调研[D]．重庆：西南大学，2015：78-85．

[16] 萨克斯 J，牛顿 J W．教育和心理的测量与评价原理[M]．王昌海，张树东，赵丽波，等译．4版．南京：江苏教育出版社，2002：301．

[17] 吴明隆．结构方程模型——AMOS的操作与应用[M]．重庆：重庆大学出版社，2010：224．

[18] 吴明隆．问卷统计分析实务——SPSS操作与应用[M]．重庆：重庆大学出版社，2010：188．

Study on Constructing Assessment Model of Geometrical Intuition Ability for Elementary School Students

ZHANG He-ping1, 3, PEI Chang-gen1, 2, SONG Nai-qing1, 2

(1. Center of Southwest University of National Innovation Center for Assessment of Basic Education Quality, Chongqing 400715, China;2. Mathematics and Statistics Institute, Southwest University, Chongqing 400715, China;3. Kaili University, Guizhou Kaili 556011, China)

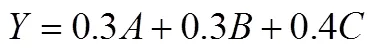
elementary school students; geometrical intuition ability; assessment indicators; assessment model

[责任编校：周学智]

G620

A

1004–9894（2017）05–0049–05

张和平，裴昌根，宋乃庆．小学生几何直观能力测评模型的构建探究[J]．数学教育学报，2017，26（5）：49-53．

2017–09–06

2015年中国基础教育质量监测协同创新中心项目——小学生数学素养发展的评价、监测与改进（201506BZK02）；贵州省2017年科技厅项目——几何直观能力测评模型构建及实证研究（黔科合LH字[2017]7164号）

张和平（1974—），男，贵州从江人，凯里学院副教授，西南大学博士生，主要从事数学教育与教育测评研究．