基于动三轴试验的层间错动带动孔压特性及能量分析

朱 凌，裴向军，崔圣华，孟祥瑞

(地质灾害防治与地质环境保护国家重点实验室(成都理工大学)，四川 成都 610059)

基于动三轴试验的层间错动带动孔压特性及能量分析

朱 凌，裴向军，崔圣华，孟祥瑞

(地质灾害防治与地质环境保护国家重点实验室(成都理工大学)，四川 成都 610059)

2008年汶川地震触发的大光包滑坡滑带形成背景是渗水层间错动带，该带强度变化是决定滑坡启动的主要因素，动孔压发展是土体材料强度劣化的根本原因，故基于系列室内动三轴试验研究该带材料孔压特性。结果表明，动载下层间错动带材料孔压快速增长，循环剪应力比越大，孔压增长越快，不同荷载条件下应变达到5%时动孔压比等于1，材料液化，根据动孔压比与振次比曲线的拟合关系提出幂函数应力模型。从能量角度描述层间错动带材料孔压增长特性，揭示出循环剪应力比对累积能量耗损与动孔压比曲线影响较小而围压对其影响较大，并进一步提出孔压增长的能量模型。

层间错动带；动孔压；应力模型；能量模型

岩体在复杂的构造背景下发生挤压或拉张破坏并且沿某一破裂面发生剪切错位形成剪切破碎带，在复杂的剪切破碎带中有一类沿层间变形的软弱带，称为层间错动带[1]。层间错动带强度很低，力学性能差，尤其在地震作用下，层间错动带的强度变化往往决定了山体的稳定性；在动荷载下孔隙水压力的增长是土体强度降低的根本原因，因此研究循环荷载下孔压的增长规律有十分重要的意义。

一直以来，众多专家学者对动荷载下的孔压增长规律进行了研究。Seed等[2]最早在等压固结不排水试验的基础上提出了循环荷载下砂的动孔压发展模式：

式中：ud——振动N次的孔压；

σ3——试样初始有效围压；

Nf——试样破坏时的振动次数；

θ——试验参数。

Finn等[3]提出在非等压固结情况下用孔隙水压力等于围压一半时的振动次数N50代替Nf，将Seed的公式进行了修改。徐志英等[4]通过对天津粉砂进行动单剪试验，得到了在偏压固结下的动孔压模型。张建民等[5]考虑土的密度、固结应力比及动荷载作用强度对孔压的影响，建立了孔压增长的A型、B型和C型曲线。因为这类模型的特点是将动孔压与施加的动应力联系起来，通过Nf隐现动应力的大小，因此统称为孔压的应力模型。孔隙水压力的应力模型无法解释动应力在发生卸荷时的反向剪缩特征，而这种现象对孔压的变化有重要的作用，同时，应力模型的建立是以室内等幅应力的动三轴试验为基础，而实际动应力幅值很复杂，不可能保持等幅应力。因此鉴于应力模型的缺陷，何广讷[6]提出使用能量法评价土体的液化势，通过有限元法算出结点处单元体积土体的振动能量，然后与相应条件下试样的界限振动能量比较,来判断土体是否液化。随后曹亚林等[7]提出动孔压的增长与土中累积耗损的能量密切相关，累积耗损能量是反映土中动孔压增长程度的一个重要物理量。王桂萱等[8]通过试验得到振幅、频率、荷载形式和荷载的不规则性对动孔压和累积耗损能量的关系没有影响，固结围压对其影响较大。刘叔灼等[9]通过饱和尾矿土不排水循环剪切试验，得出在循环荷载作用下孔压的增大与塑性应变和黏滞累积能量耗损有关，孔压增长与能量耗损的关系受循环应力比、轴-径向固结应力比的影响。郭莹等[10]通过不排水循环单剪以及轴向和扭转双向耦合循环剪切试验，建立了复杂应力条件下饱和松砂的动孔压增长与能量耗损的关系。由于能量分析法将循环荷载下孔压的升高与土颗粒重新排列消耗的能量联系起来，能更加直接地反映孔压增长过程，并且能量是标量，可使用迭加原理来解决复杂应力条件下孔压的增长过程，因而孔压的能量模型比应力模型更为可靠。

前人对动荷载下不同材料的孔压发展过程进行了大量研究，但多数学者仅针对某一种粒径范围的理想材料进行研究，与实际差别较大。本文通过现场调查，结合实地情况，对2008年汶川地震触发的最大规模滑坡大光包滑坡层间错动带材料进行动三轴试验，研究在循环荷载下该材料的孔压增长特性，建立层间错动带动孔压增长应力模型和能量模型，为预测地震作用下大光包滑坡层间错动带的孔压增长提供借鉴。

1 试验基本情况

1.1地质背景

大光包滑坡位于绵阳市安县高川乡，是2008年汶川地震触发的最大规模滑坡，体积约11.59×108m3,堆积体最大厚度约515 m，主滑方向63°[11]。滑坡启动后在南侧暴露出长约1.8 km的顺层滑带，岩性是震旦系灯影组富藻白云岩，通过在滑面打钻和挖探槽发现不同深度物质结构差异较大，在滑面以下0～1 m处主要是砂土，1 m以下岩体高度碎裂化，随深度增加岩体碎裂化程度减小[12～13]。为研究岩质滑坡中这种滑带土的成因。作者所在团队根据滑带产状在大光包滑坡山体背后开挖长约20 m的平硐(图1)。

图1 大光包滑坡Fig.1 Daguangbao landslide

从平硐中找到一层3～5 m厚的层间错动带，该带与上覆白云岩地层有明显的分界，且该错动带与滑坡南侧滑面残留的滑带土物质成分基本一致。表明滑坡滑带产生于震旦系灯影组富藻白云岩的层间错动带[12～13]。

1.2试验材料

通过在平硐中的调查，层间错动带土质材料是白云岩在多期次的构造活动下被强烈剪切、碾磨形成，颗粒分布不均匀，局部夹有角砾，从平硐中可以明显看到层间错动带有地下水渗出，材料基本处于饱水状态，本次试验材料取自该层间错动带，由于山体后缘并未受到滑坡运动过程的影响，因此该材料能反映震前大光包滑坡滑带的特性。

震旦系灯影组富藻白云岩主要由泥晶藻白云石基质和亮晶白云石胶结物组成。由于试验条件限制，剔除大于5 mm的颗粒，样品主要由砂粒(0.075～2 mm)组成，约占总质量的56%。图2是试样的颗分曲线。

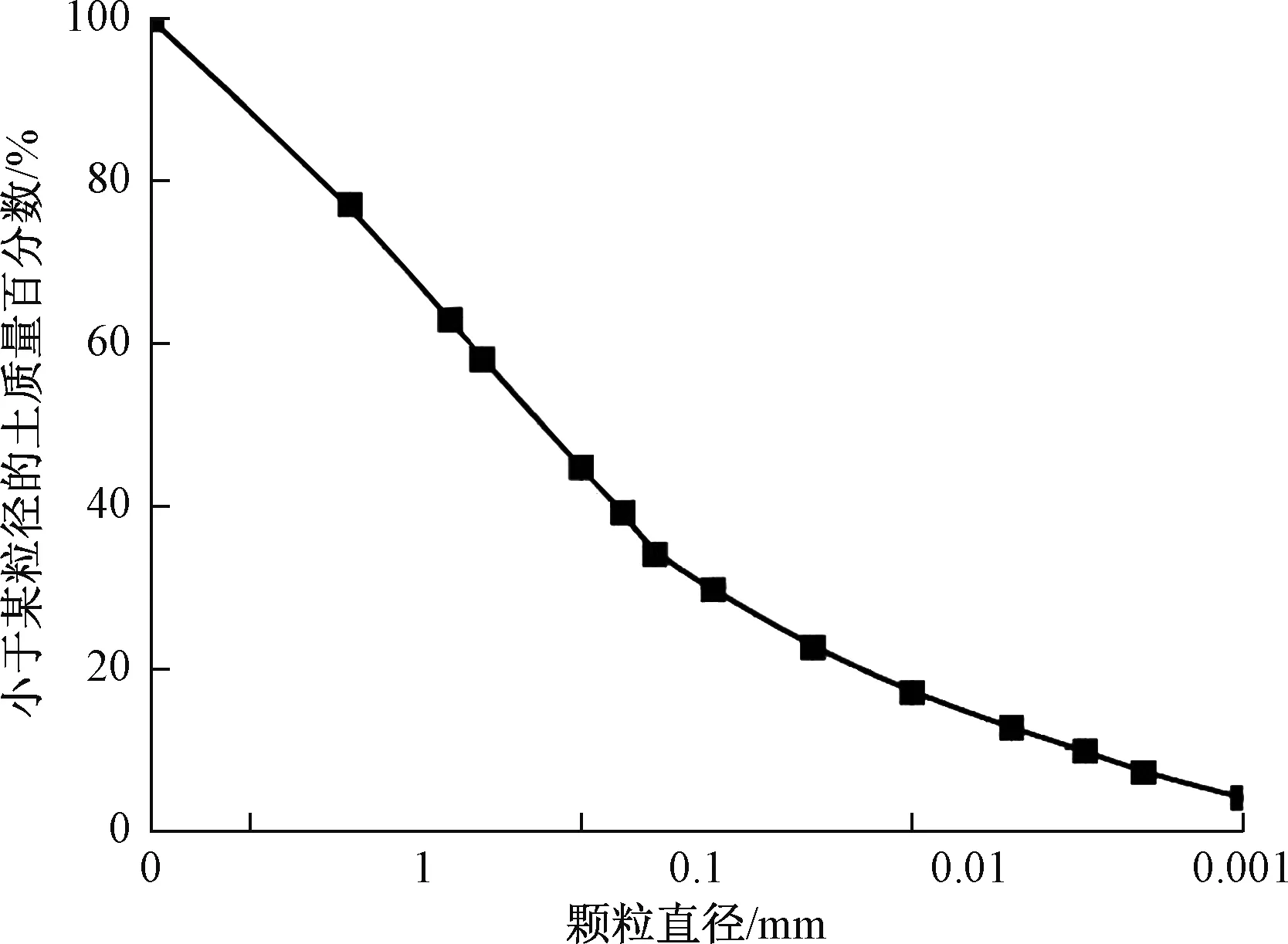
图2 颗分曲线Fig.2 Gradation curve

在天然条件下大光包滑坡层间错动带材料天然含水率较高，测试得到天然含水率达到9.44%，接近于材料液限，表1是试样的物理性质参数指标。

表1 试样物理性质参数指标

1.3试验仪器

试验使用地质灾害与地质环境保护国家重点实验室的MTS810 Teststar程控伺服土动三轴试验机(图3)，该仪器可加轴向振动荷载0～25 kN，围压0～2 MPa，频率1～10 Hz。

图3 MTS810土动三轴试验机Fig.3 MTS810 soil dynamic triaxial testing machine

1.4试验方法

本次试验使用直径50 mm，高100 mm的圆柱体样品。将烘干的重塑土配制10%的初始含水率后，在密闭环境中静置24 h使水分均匀分布，然后按照干密度1.8 g/cm3确定每层土的重量，分层击实，为使制样均匀将接触面刮毛。

使用反压饱和法对试样饱和，先设置初始围压20 kPa，向样品中通CO2约2 h，然后使用1 h水头通水约1.5 h后关闭阀门测试B值，此时B值约为0.3。后施加反压，每级增加20 kPa，为防止试样膨胀而破坏，围压与反压之差稳定在20 kPa，每级应力施加后稳定20 min再施加下一级，当B>0.95认为试样达到饱和。饱和完成后分别施加围压100，150和200 kPa进行等压排水固结，在关闭出水阀门5 min内孔压不变认为固结完成。然后施加1 Hz的正弦等幅循环荷载，在不同循环剪应力比(σd/2σ3)0.2，0.3和0.4下振动，应变达到5%认为试样破坏。

2 试验结果

图4是层间错动带在围压100 kPa、循环剪应力比0.3时的动孔压比(ud/σ3)、应变(εd)和动应力(σd)时程曲线。从图4(a)可以看出，在振动初始阶段孔压上升较快，20 s时动孔压比达到0.2，随后孔压增长速率稍微放缓，振动40 s后动孔压比约为0.35，在该时间点后孔压增长速率随振动时间逐渐加快，80 s时动孔压比达到0.9，随后增速减缓，试验结束(应变达到5%)时动孔压比基本达到1。由图4(b)可以看出，在0～70 s时应变增长缓慢，仅达到1.5%；经过某一临界点后应变迅速增长，在很短时间内达到应变破坏标准(5%)。由图4c可以看出，在0～60 s时动应力基本稳定在60 kPa，60～70 s有小幅度的减小，随后动应力衰减速度增大，在80 s时仅有40 kPa。

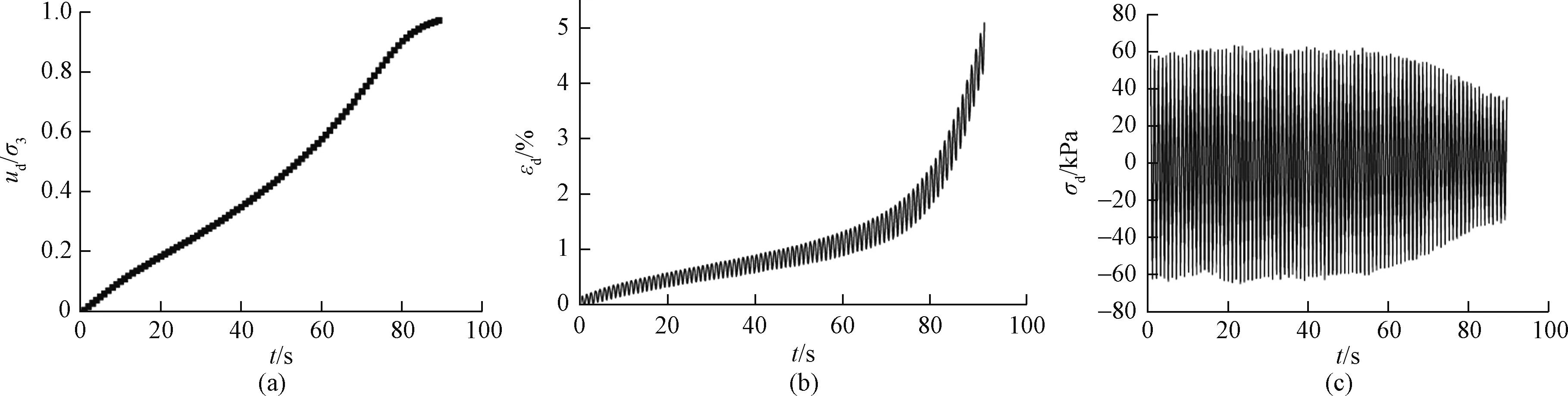
图4 动三轴典型时程曲线Fig.4 Typical epoch curve of the dynamic triaxial test

3 动孔压增长特性

图5是不同循环剪应力比下动孔压比与振动次数(N)关系曲线，从图中可以看出：(1)随着振动次数增加孔隙水逐渐累积，动孔压比增大；(2)在不同循环剪应力比下达到应变破坏标准时(εd=5%)，动孔压比均大于0.95，试样基本液化；(3)循环剪应力比越大，孔压增长越快，达到相同动孔压比需要的振动次数越少。

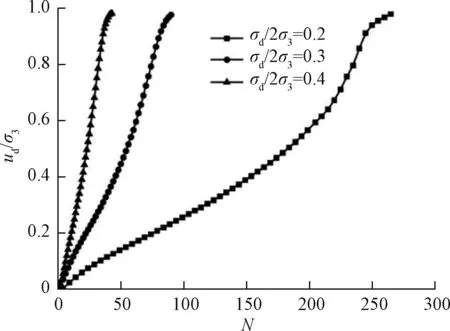
图5 不同循环剪应力比下ud/σ3与N关系曲线Fig.5 Relationship between ud/σ3 and N under different cyclic shear stress ratios

从图6中看出不同循环剪应力比下动孔压比与振次比曲线形态具有差异，在循环剪应力比较小时(σd/2σ3=0.2，0.3)，振动初始阶段孔压增长速率较快，振次比在0.2～0.5时孔压增速降缓，随后动孔压比又迅速增长，振次比到0.9时动孔压比趋于稳定。在循环剪应力比较大时(σd/2σ3=0.4)，振动前期孔压基本匀速增长，振次比达到0.9以后动孔压比稳定。

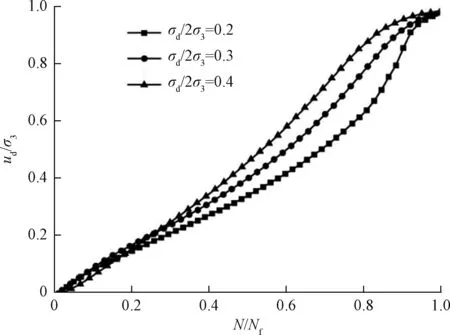
图6 不同循环剪应力比下ud/σ3与N/Nf关系曲线Fig.6 Relationship between ud/σ3 and N/Nf under different cyclic shear stress ratios

循环剪应力比一定，不同围压下的动孔压比与振动次数关系曲线如图7所示，可以看出不同围压100，150，200 kPa下动孔压增长曲线形态相似，随着振次增加孔压增长较快，在动孔压比达到约0.95时孔压增速降缓并趋于稳定，在不同围压下试样均能达到液化。

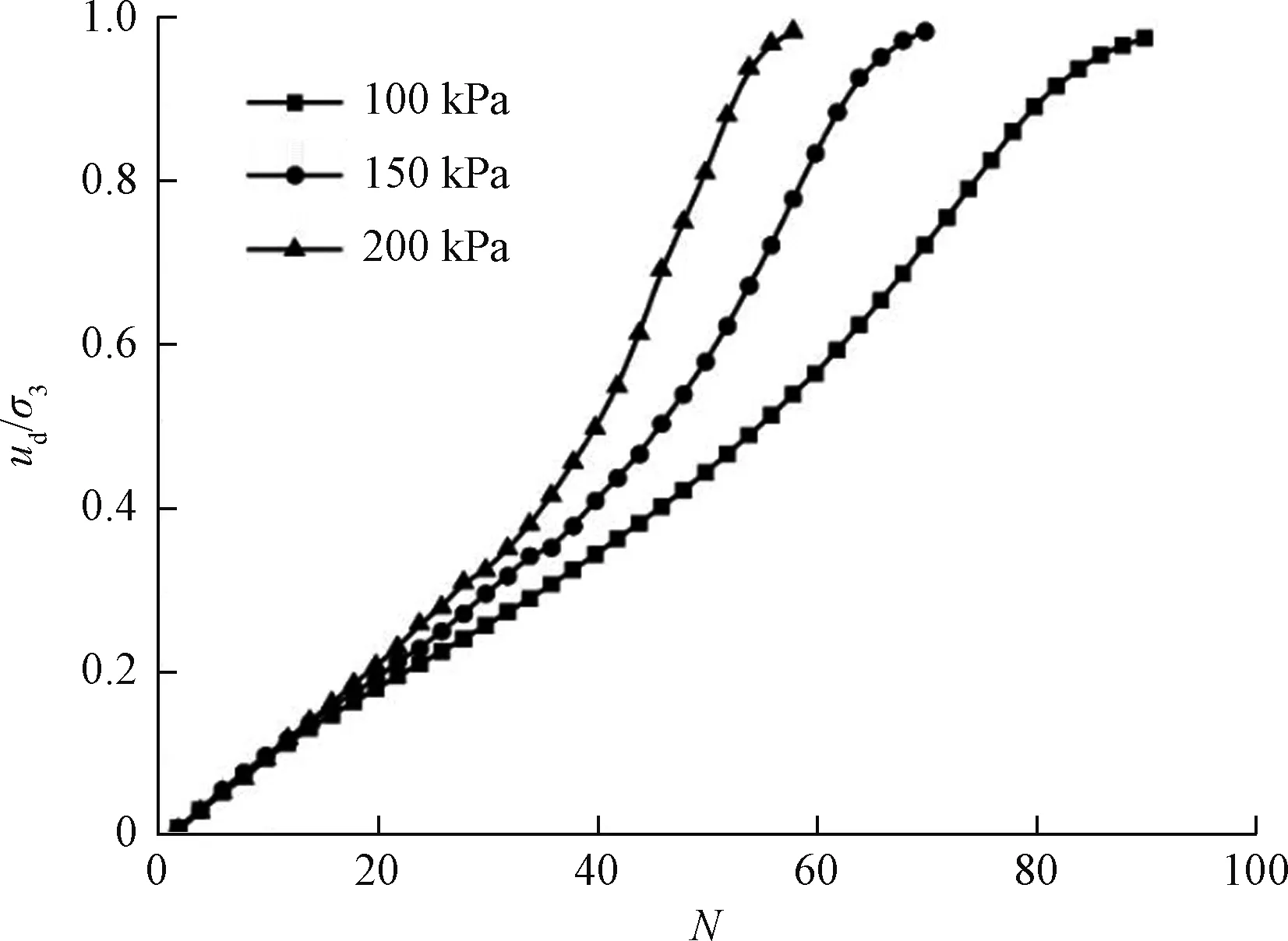
图7 不同围压下ud/σ3与N关系曲线Fig.7 Relationship between ud/σ3 and N under confining pressure

图8是不同固结围压下动孔压比与振次比的关系曲线，从图中可以看出不同围压下各试验点分布在较窄的范围内，离散小。尽管在振次比一定时，动孔压比随围压的增大而稍有减小，但这种差值很小，基本上没有变化，因此可认为围压对动孔压比与振次比曲线没有影响，在不同固结围压下的动孔压比与振次比的关系曲线可近似归一。

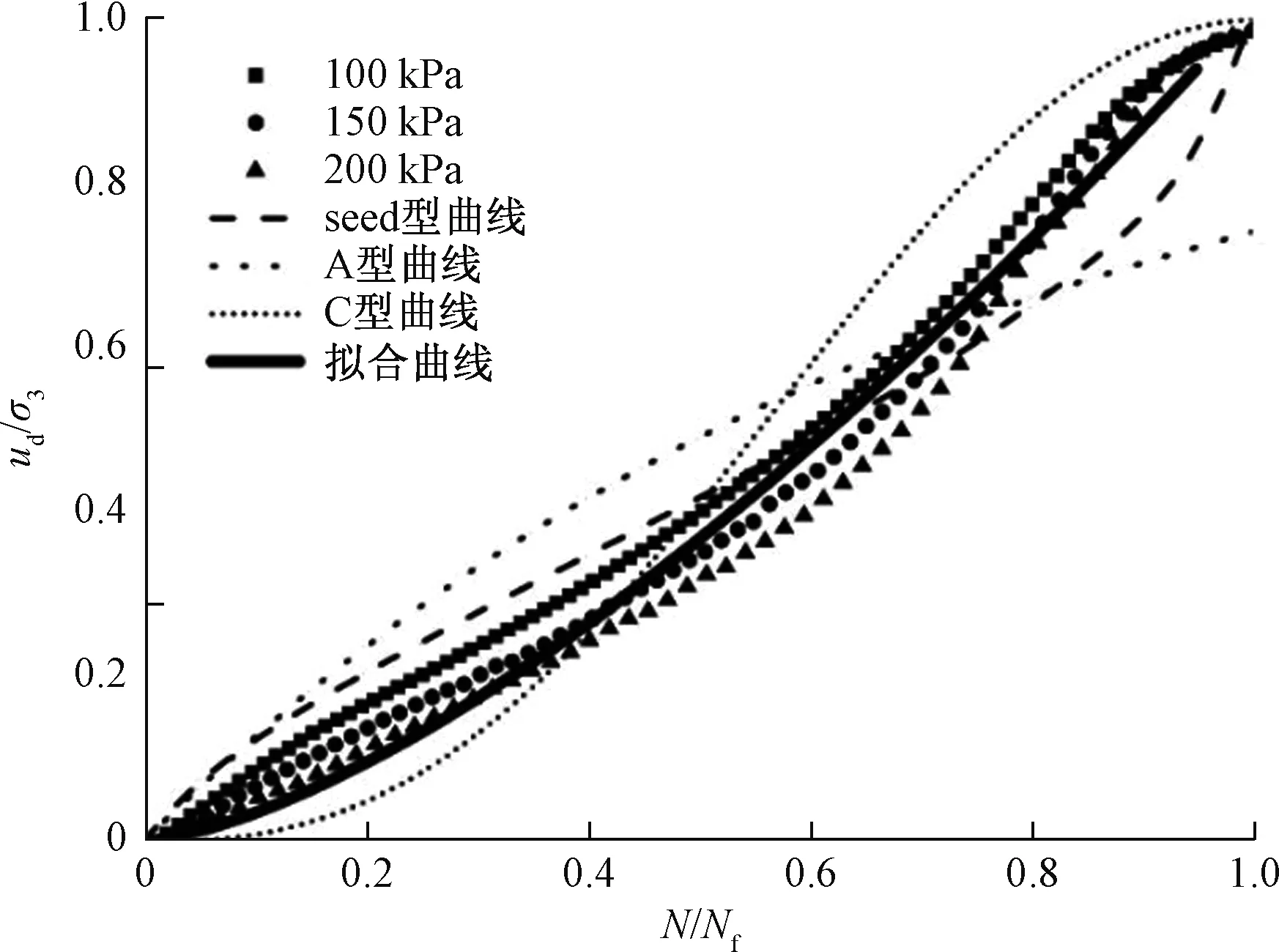
图8 不同围压下ud/σ3与N/Nf关系曲线Fig.8 Relationship between ud/σ3 and N/Nfunder confining pressure

分别使用Seed，张建民A型、C型曲线对动孔压比与振次比关系曲线进行拟合，发现拟合效果较差(图8)，均不能准确反映孔压的增长情况，因此本文通过origin软件对数据进行多次的分析拟合，发现幂函数拟合效果较好，表达式为：

式中：Nf——试样破坏时的振动次数；

a，b——试验参数，a=1.0122，b=1.468，R2=0.9912。

4 动孔压增长的能量分析

外界振动荷载作用会给土体传递能量，由于土颗粒之间的粘结力较弱，在振动时会发生颗粒之间的相对运动和重新排列，这个过程会损耗一定的能量。何广讷等[14]将其概括为输入能量Ei、损耗能量W和输出能量E0，3种不同能量满足表达式：

饱和土由土颗粒和孔隙水两相组成，在振动过程中土颗粒的相对运动和重新排列不仅会消耗一定的能量，而且使土体压密、孔隙水压力增长。因此在振动过程中的能量损耗是反映土体孔隙水压力增长的一个重要指标，本文考虑使用能量分析法计算层间错动带中孔隙水压力的增长，建立一个孔隙水压力增长的能量模型。

4.1计算方法

何广讷等[14]提出“土中振动能量的耗损主要产生于循环剪力荷载下土颗粒发生相对滑移和重新排列而出现的应力应变滞后反应”。因此一般采用应力应变滞回曲线的面积表示循环荷载振动一周在土中耗损的能量。前人多将应力应变滞回曲线简化成椭圆图形，通过计算椭圆的面积来求出损耗能量，但由于滞回曲线不是标准的椭圆，使用这种方法误差较大。

本文根据每相邻两个数据点对应的应力、位移值将滞回曲线划分成多个小多边形，通过计算每个小多边形的面积(图9)，累积相加得到滞回曲线的面积。

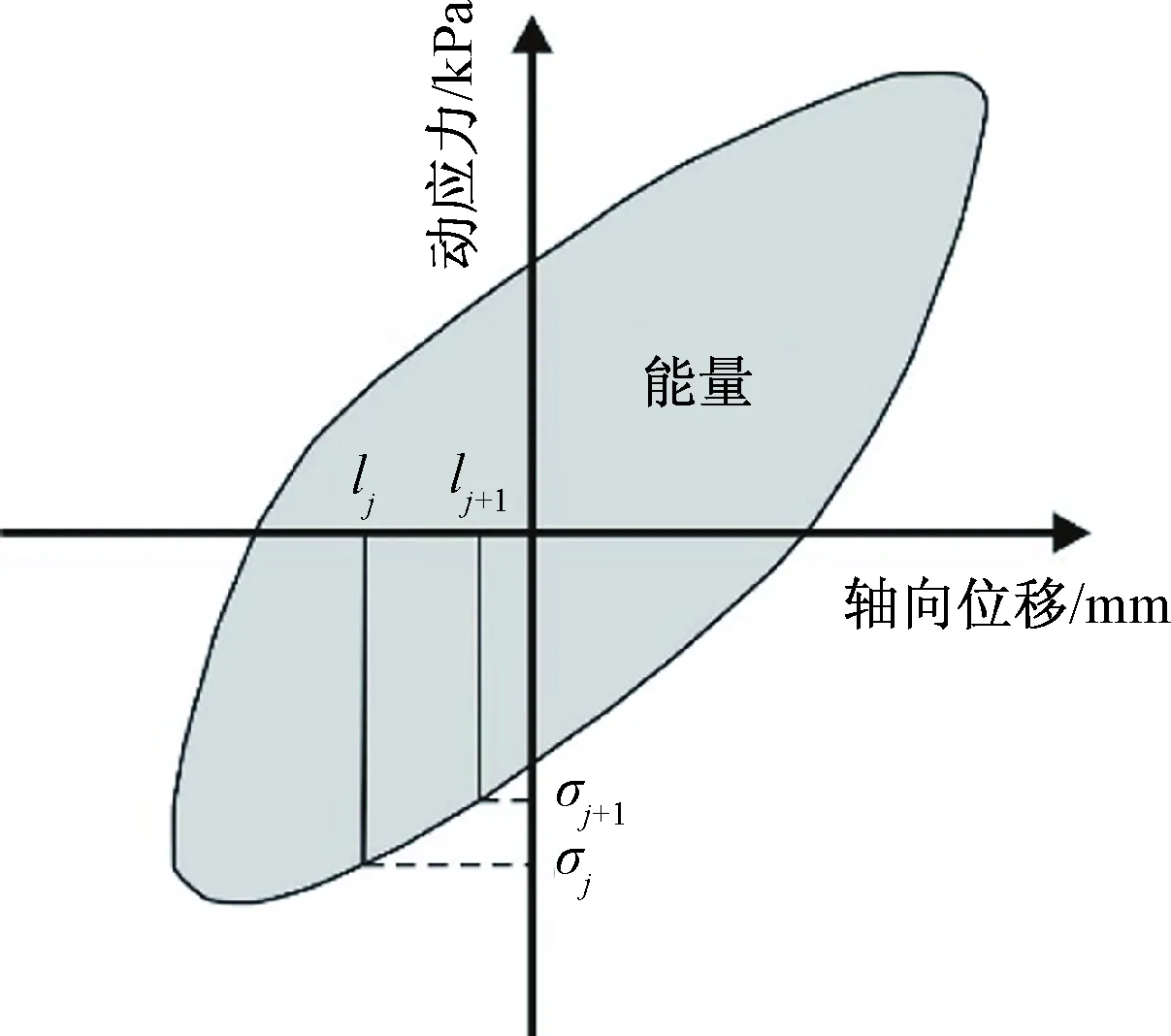
图9 滞回曲线Fig.9 Hysteresis curve

使用MTS土动三轴试验机可以设置在每个循环振次内得到的应力应变数据个数，为了尽可能使计算的滞回曲线面积准确，本次试验设置每个循环振次得到40组应力应变数据，滞回曲线面积计算公式如下：

式中：Si——第i个循环振次滞回曲线的面积；

σj，lj——一个循环周期内第j个数据点对应的动应力和轴向位移。

因此第i周累积耗损能量值就等于第1周到第i周滞回曲线面积的和：

在循环荷载作用下，孔隙水压力会随应力变化波动，同时，随着振次增加孔压会逐渐累积，本文选取每个循环周期孔压的平均值作为分析点，研究动孔压与累积耗损能量的关系。公式如下：

式中：udi——第i周的平均动孔隙水压力；

ui,max，ui,min——第i周的最大孔隙水压力和最小孔隙水压力值。

4.2能量耗散规律

如图10所示，在振动过程中需要不断消耗能量，随振次增加累积耗损能量将会逐渐增大。同时，在振动过程中每一循环振次的耗损能量也在逐渐增大，如在振动初始阶段(1～10周)每周次平均循环耗损能量约为28.9 J/m3。而在振动后期(31～40周)每周次平均耗损能量约为55.5 J/m3。但每周次的耗损能量增大到一定值后将基本不会随着振次增加而增大，说明在振动过程中能量耗损有一定的极限值。

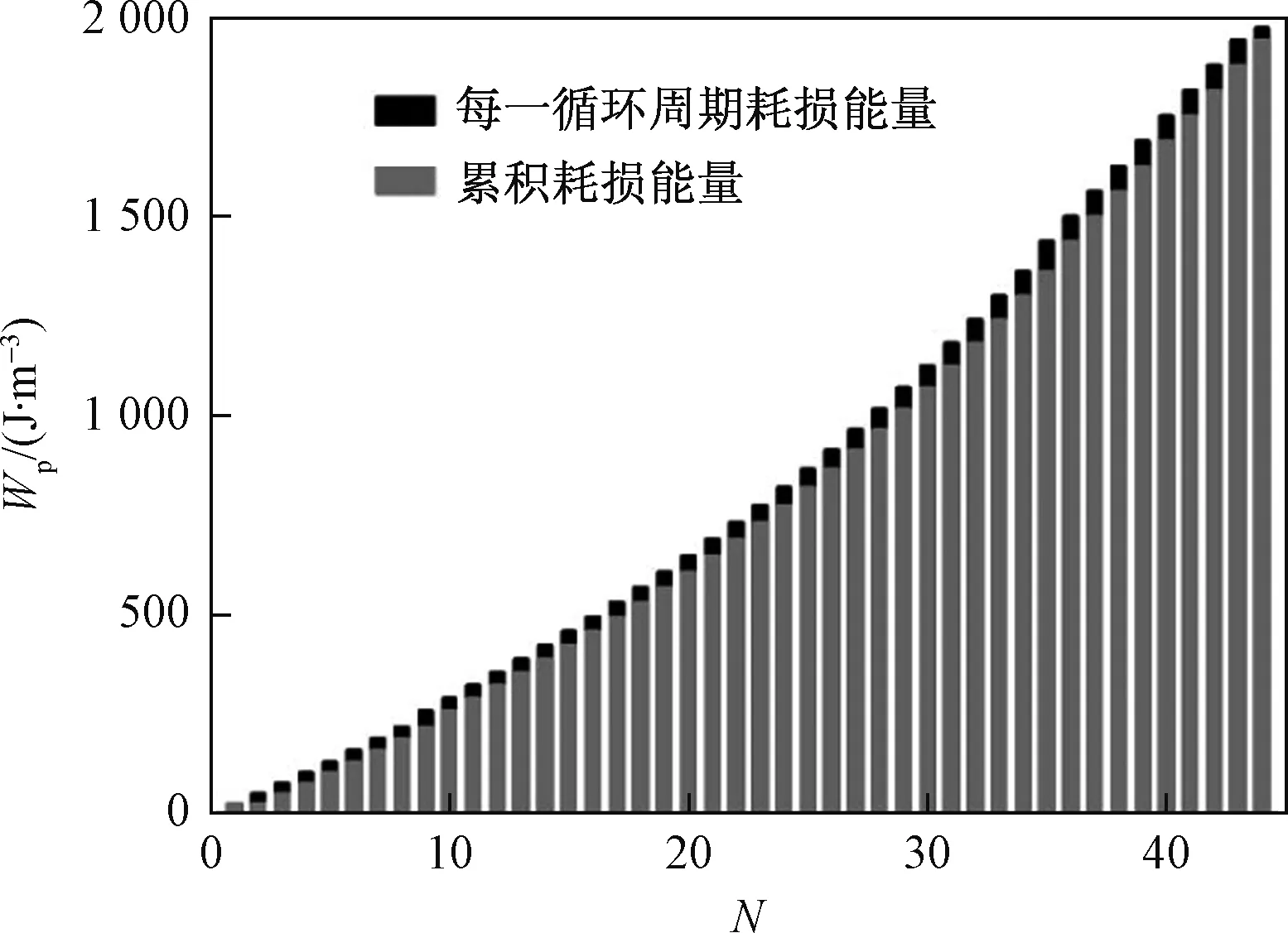
图10 Wp与N关系曲线Fig.10 Relationship between Wp and N

4.3动孔压比与累积耗能关系

图11是不同循环剪应力比下动孔压比与累积耗损能量的关系曲线，从图中可以看出：(1)在不同循环剪应力比下动孔压比随累积耗损能量增加而上升。(2)循环剪应力比对动孔压比与累积耗损能量曲线影响较小，达到相同动孔压比需要的能量基本相同。(3)根据动孔压比的增长特征，曲线可以分为两个阶段：①动孔压比在0～0.9时，该阶段累积损耗能量增长较快，孔压快速上升，曲线斜率较大。②动孔压比在0.9～1时，该阶段累积损耗能量增长较快，动孔压基本保持稳定，曲线斜率小。

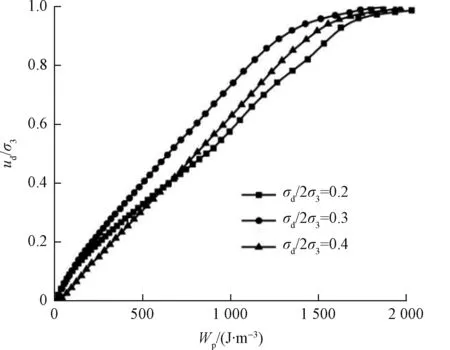
图11 不同循环剪应力比下ud/σ3与Wp关系曲线Fig.11 Relationship between ud/σ3 and Wp under different cyclic shear stress ratios

循环剪应力比一定，不同围压100，150和200 kPa下动孔压比与累积损耗能量关系曲线如图12所示，从图12中可以看出，不同围压下动孔压比与累积能量损耗的关系曲线形态与图11基本相同，前期孔压增长较快，后期趋于稳定。但围压对动孔压比与累积耗损能量曲线影响较大，围压越大，达到相同动孔压比累积耗损的能量越多，围压越小，累积耗损能量相对较小。

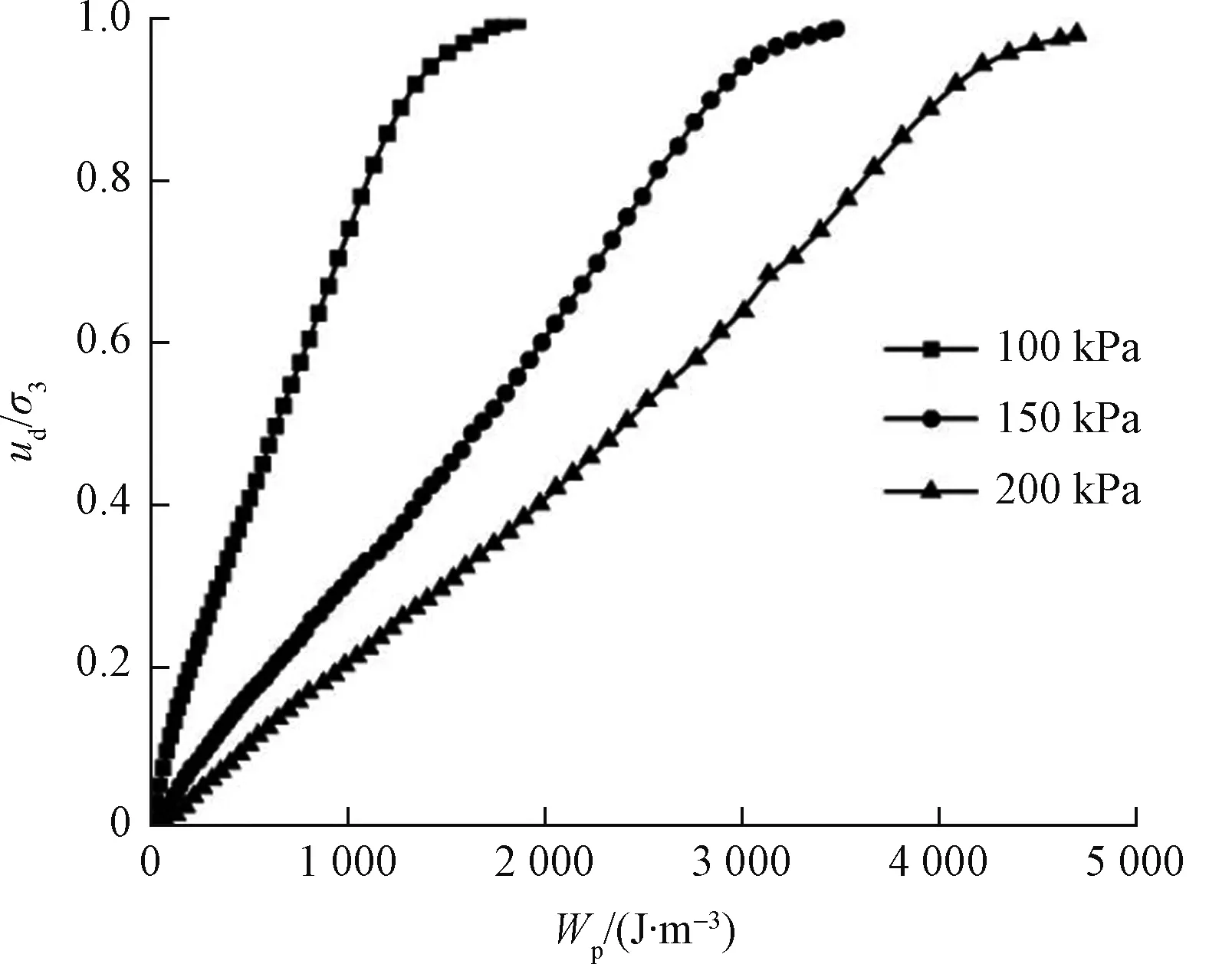
图12 不同围压下ud/σ3与Wp关系曲线Fig.12 Relationship between ud/σ3 and Wp under confining pressure

4.4动孔压比与累积耗能归一化模型

根据上述研究，孔隙水压力的增长与累积耗损能量有关，而循环剪应力比对动孔压比与累积耗损能量关系曲线影响较小，围压对曲线影响较大，为建立不受围压影响的耗损能量归一化曲线，引入试样破坏时的累积耗损能量值进行归一化无量纲处理。将归一化结果示于纵坐标是对数坐标的平面内。得到如图13所示的结果。

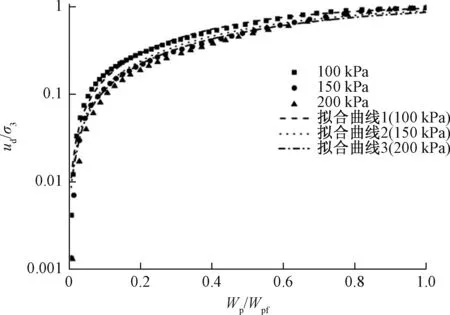
图13 不同围压下ud/σ3与Wp/Wpf关系曲线Fig.13 Relationship between ud/σ3 and Wp/Wpf under confining pressure

使用origin软件对归一化曲线多次分析拟合，发现指数函数拟合效果较好，得到如下拟合公式：

式中：Wpf——试样破坏时的累积耗损能量；

a——试验参数，随固结围压的增大而减小。

拟合结果见表2。

表2 拟合结果

5 讨论

大光包滑坡层间错动带在地质历史时期经历了多次构造剪切和地下水胶结的循环作用。角砾和岩屑沿着错动方向定向排列，渗水作用使土颗粒之间的联结减弱，在多次的构造力作用下错动带颗粒之间的原有结构发生松弛和破坏，材料结构性很差。因此重塑土样动孔压特征基本能够反映原始层间错动带孔压变化规律。根据采样在室内筛分得到的结果，层间错动带角砾含量小于10%，在角砾含量较小时，试样的骨架主要由砂颗粒之间的相互接触形成，孔压增长特性以砂粒控制为主，角砾影响很小，因此本文去掉大于5 mm的角砾进行试验对孔压增长影响较小。然而虽然本文使用材料砂粒占比较大，但和常规砂土的动孔压增长规律相比仍然有较大差异，张建民等[5]将不同条件的砂土动孔压增长过程归纳为A型、B型和C型曲线，砂土的孔压增长过程会根据土的密度、固结应力比和动荷载作用强度由A型到C型变化，但本文得到的试验结果用张建民提出的三类曲线拟合效果较差，使用幂函数拟合效果较好，这主要与试样中含有一定比例的角砾和粘粒有关，该层间错动带材料动孔压增长规律与常规砂土相比差异较大。

6 结论

(1)在动荷载作用下层间错动带孔压增长较快，循环剪应力比越大，孔压增长越快，应变达到5%时动孔压比达到1。

(2)不同固结围压下动孔压比与振次比关系曲线离散型较小，可近似归一，用幂函数拟合效果较好，表达式为：ud/σ3=a×(N/Nf)b。

(3)使用能量分析法研究层间错动带中孔隙水压力的增长规律，发现随累积耗损能量增加，孔压逐渐增大。循环剪应力比对动孔压比与累积耗损能量曲线影响较小，围压对曲线影响较大。

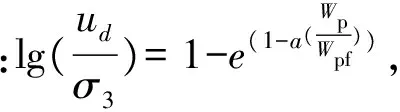
[1] 江权,冯夏庭,周辉,等.层间错动带的强度参数取值探讨[J]. 岩土力学,2011,32(11):3379-3386.[JIANG Q, FENG X T, ZHOU H,etal. Discussion of strength value for interlayer shear belt[J]. Rock and Soil Mechanics,2011, 32(11):3379-3386.(in Chinese)]

[2] SEED H B, LYSMER J, MARTIN P P. Pore-water pressure changes during soil liquefaction[J].Journal of the Geotechnical Engineering Division, 1976, 102(4): 323-346.

[3] FINN W D L, LEE K W, MARTIN G R. An Effective Stress Model for Liquefaction[J]. ASCE, 1977,103(GT6).

[4] 徐志英,沈珠江.地震液化的有效应力二维动力分析方法[J].河海大学学报，1981,9(3):1-14.[XU Z Y, SHEN Z J. 2-D Dynamic analysis of effective stresses of seismic liquefaction[J]. Journal of Hohai University, 1981,9(3):1-14.(in Chinese)]

[5] 张建民,谢定义. 饱和砂土振动孔隙水压力增长的实用算法[J]. 水利学报,1991,22(8):45-51.[ZHANG J M，XIE D Y. Practical calculation of dynamic pore water pressure in saturated[J].Journal of Hydraulic Engineering，1991,22(8):45-51.(in Chinese)]

[6] 何广讷.评价土体液化势的能量法[J]. 岩土工程学报,1981,3(4):11-21.[HE G N. Energy analysis procedure for evaluating soil liquefaction potential[J]. Chinese Journal of Geotechnical Engineering, 1981,3(4):11-21.(in Chinese)]

[7] 曹亚林,何广讷,林皋. 土中振动孔隙水压力升长程度的能量分析法[J]. 大连工学院学报,1987,26(3):83-89.[CAO Y L, HE G N, LIN G. An energy approach for analysing the development of cyclic pore water pressure[J]. Journal of Dalian Institute of Technology, 1987, 26(3):83-89.(in Chinese)]

[8] 王桂萱,桑野二郎,竹村次朗. 循环荷载下砂质混合土孔隙水压力特性研究[J].岩土工程学报,2004,26(4):541-545.[WANG G X, Jiro Kuwano, Jiro Takemura. Study on excess pore water pressures of sands mixed with clays under cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2004,26(4):541-545.(in Chinese)]

[9] 刘叔灼,李慧子,单毅,等. 基于能量法的尾矿土动孔压模型研究[J]. 岩土工程学报,2016,38(11):2051-2058.[LIU S Z, LI H Z, SHAN Y,etal. Energy method for analyzing dynamic pore water pressure model for tailing soil[J]. Chinese Journal of Geotechnical Engineering, 2016,38(11): 2051-2058.(in Chinese)]

[10] 郭莹,刘艳华,栾茂田,等. 复杂应力条件下饱和松砂振动孔隙水压力增长的能量模式[J].岩土工程学报,2005, 27(12):1380-1385.[GUO Y，LIU Y H, LUAN M T,etal. Energy-based model of vibration-induced pore water pressure build-up of saturated loose sand under complex stress condition[J]. Chinese Journal of Geotechnical Engineering, 2005,27(12):1380-1385.(in Chinese)]

[11] 李天涛,裴向军,黄润秋. 强震触发大光包巨型滑坡运动特征研究[J]. 水文地质工程地质,2014,41(2):116-121.[LI T T, PEI X J, HUANG R Q. A study of motion features of the Daguangbao large-scale landslide induced by the Wenchuan Earthquake[J]. Hydrogeology & Engineering Geology,2014,42(2):116-121.(in Chinese)]

[12] 黄润秋,裴向军,崔圣华. 大光包滑坡滑带岩体碎裂特征及其形成机制研究[J]. 岩石力学与工程学报,2016,35(1):1-15.[HUANG R Q, PEI X J, CUI S H. Cataclastic characteristics and formation mechanism of the rock mass in sliding zone of Daguangbao landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(1):1-15.(in Chinese)]

[13] 裴向军,黄润秋,崔圣华,等. 大光包滑坡岩体碎裂特征及其工程地质意义[J]. 岩石力学与工程学报，2015，34(增刊1):3106-3115.[PEI X J, HUANG R Q, CUI S H,etal. The rock mass cataclastic characteristics of Daguangbao landslide and its engineering geological significance[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(Sup 1): 3106-3115.(in Chinese)]

[14] 何广讷,曹亚林. 饱和无粘性土动力反应的能量分析原理与方法[J]. 土木工程学报,1990,23(3):2-10.[HE G N, CAO Y L. Fundamentals and applications of the energy method in soil dynamics[J]. China Civil Engineering Journal,1990,23(3):2-10.(in Chinese)]

责任编辑：张明霞

Dynamicporepressureofthebeddingfaultmaterialwithinthebasallayerandenergyanalysisbasedonthetriaxialtest

ZHU Ling, PEI Xiangjun, CUI Shenghua, MENG Xiangrui

(StateKeyLaboratoryofGeohazardPreventionandGeoenvironmentProtection(ChengduUniversityofTechnology),Chengdu,Sichuan610059,China)

The Daguangbao landslide was triggered by the 2008 Wenchuan earthquake. The sliding zone formed in a bedding fault along which groundwater could be found to flow. The key factor of the landslide initiation is the strength change in the bedding fault under the earthquake effect, and the development of dynamic pore pressure is the root cause of the material strength of soil degradation. Therefore, a series of dynamic triaxial tests were conducted on the materials to examine the property of dynamic pore pressure. The results show that the dynamic pore pressure of the bedding fault material grows faster under the dynamic load, and the dynamic pore pressure increases faster when the cyclic shear stress ratio is greater. The dynamic pore pressure ratio is basically equal to the confining pressure when the strain reaches 5%, and the materials are liquefied. A stress model of a power function according to the relationship of the dynamic pore pressure ratio and cycle ratio is proposed. The response of pore water pressure can be described by using energy, revealing that the cyclic shear stress ratio has less effect on the relationship of the dynamic pore pressure ratio and cycle ratio. The confining pressure has a great influence on the relationship of the dynamic pore pressure ratio and cycle ratio. The theoretical energy model of dynamic pore pressure is further proposed.

bedding fault; dynamic pore pressure; stress model; energy model

TU411.7

A

1000-3665(2017)05-0072-08

裴向军(1970-)，男，教授，博士生导师，主要从事地质灾害、工程边坡稳定性评价及工程治理教学和研究工作。

E-mail:peixj0119@tom.com

10.16030/j.cnki.issn.1000-3665.2017.05.12

2017-02-23;

2017-04-25

国家创新研究群体科学基金项目资助(41521002)；国家自然科学基金项目资助(41572302)

朱凌(1993-)，男，硕士研究生，主要从事地质灾害防治研究工作。E-mail：1325935632@qq.com