跨季节蓄热型地源热泵热传递规律研究

吴 晅，路子业，刘 卫，梁盼龙，田雪凯，金 光

(1.内蒙古科技大学能源与环境学院，内蒙古 包头 014010；2.储运与建筑工程学院，中国石油大学(华东)，山东 青岛 266580)

跨季节蓄热型地源热泵热传递规律研究

吴 晅1，路子业1，刘 卫1，梁盼龙1，田雪凯2，金 光1

(1.内蒙古科技大学能源与环境学院，内蒙古 包头 014010；2.储运与建筑工程学院，中国石油大学(华东)，山东 青岛 266580)

基于有限元分析法，建立了准三维非稳态传热模型。在试验验证的基础上，分析了跨季节蓄热型地源热泵蓄热过程中土壤温度、单位井深换热量、热作用半径随热泵运行时间的变化规律，讨论了土壤结构、入口水温、入口质量流量、热泵运行模式等对土壤传热规律的影响，并研究了土壤热平衡问题。结果表明：同一半径不同深度处，土壤温度增长幅度随土壤热扩散率的增加而增大；土壤热作用半径随热泵运行时间及入口水温的升高而增加，并逐渐趋于稳定；间歇运行模式下，地埋管附近土壤温度及换热量均呈波动式变化，且当径向距离大于0.3 m时，与连续模式一致；在满足换热量的情况下，流体质量流量不宜过大；系统运行一个周期(360 d)后土壤温度基本可以恢复，且流体入口温度不宜低于40 ℃。

地源热泵；地埋管；热作用半径；运行模式；土壤热平衡

土壤热失衡是影响地源热泵系统运行效率和寿命的主要因素，其产生的主要原因是热泵在实际运行过程中，从土壤中取热量与蓄热量不相等，造成土壤温度偏离初始温度。土壤热失衡在我国北方地区尤为突出，由于我国北方地区冬季热负荷远大于夏季冷负荷，热泵长期运行导致土壤蓄、取热量严重失衡，造成热泵机组不能正常运行而失效[1～2]。

为了解决上述问题，国内外学者做了大量的研究。杨卫波等[3]提出热泵间歇运行模式与太阳能蓄热等方式缓解土壤热失衡，其研究表明：合理的间歇运行模式有利于地埋管附近土壤温度的恢复，太阳能蓄热技术的应用能很好地补偿季节带来的负荷差。李新国等[4]基于TRNSYS平台对天津地区太阳能-地源热泵系统蓄热和取热进行了研究，得出太阳能跨季节蓄热技术能够提高冬季热泵制热系数，确保热泵机组的正常运行。王芳等[5]提出将相变材料用于地源热泵回填材料区域，得出相变材料不仅对地埋管换热器换热过程土壤温度变化起到缓解作用，同时能够保证系统的COP处于最佳范围。Tian等[6]提出了AHC-GCHP(空气源-地源热泵系统)混合系统，研究表明：该系统能有效解决土壤热平衡问题和提高系统COP。Yang等[7]对影响土壤热失衡问题的因素做了研究，得到土壤导热系数、热扩散率越大，土壤热失衡的程度越小，埋管的合理布置能够有效缓解土壤热堆积。You T等[8]提出热虹吸(HCUT)方案及混合式地源热泵系统(GSAHP)并在多个城市进行测试，结果显示该方案能够缓解热泵全年运行过程中的热不平衡率，确保系统稳定高效运行，并且相对传统热泵系统能减少约15%的电能消耗。Rabin Y等[9]基于理论分析对相变材料PCM在热泵换热性能方面做了大量研究，得出PCM能够缓解热泵取热速率提高土壤温度恢复率。

然而，以上研究主要侧重于热泵系统运行效率、回填材料的研究及蓄热型地源热泵在特定地区的适宜性分析，而对跨季节蓄热型地源热泵蓄热过程中地埋管传热规律的研究甚少，但这方面的研究对于跨季节蓄热型地源热泵在实际工程上的应用至关重要。查阅相关文献，发现对于蓄热型地源热泵在内蒙中部地区应用的研究甚少。为此，本文针对内蒙中部地区土壤蓄热过程地埋管传热规律进行了研究，讨论了不同层土壤、入口水温、入口质量流量和热泵运行模式等对竖直地埋管传热规律的影响，最后对蓄热型地源热泵全年运行(蓄热-恢复-取热)过程中土壤温度的变化规律进行了分析，旨在为土壤热失衡问题的解决及蓄热型地源热泵在内蒙中部地区的应用提供理论指导。

1 竖直U型地埋管热传递模型

1.1物理模型

由于竖直U型地埋管几何形状的特殊性和土壤(多孔介质)传热的复杂性，为研究结果能够更加真实地反映地埋管实际传热规律，文中对模型做了以下假设：

(1)U型地埋管在钻井内对称分布，同时地埋管换热器与土壤间接触紧密忽略接触热阻。

(2)土壤及地埋管均为均质各向同性的材料，且热物性参数不随温度的变化而改变。

(3)不考虑土壤中水分迁移引起的换热量，认为土壤中的传热为多孔介质传热问题。

(4)由于钻井较深(20～200 m)，而地埋管进、出口温差(3～5 ℃)较小，因此可以认为单位微元管段流体对应的同一层土壤温度不变。

(5)基于假设4，忽略地埋管纵向传热，认为热量在土壤中的传递仅沿半径方向。

(6)采用当量直径法，将竖直U型地埋管等效为一当量直径的单管[10]。

deq=(2dpoDU)1/2

(1)

式中：dep——当量管直径/m；

dpo——U型地埋管外径/m；

DU——U型管管脚之间的距离/m。

竖直U型地埋管热传递物理模型，见图1。流体以入口温度Tin进入U型地埋管一端，与土壤发生充分热交换后以温度Tout流出，达到与周围土壤换热的目的。

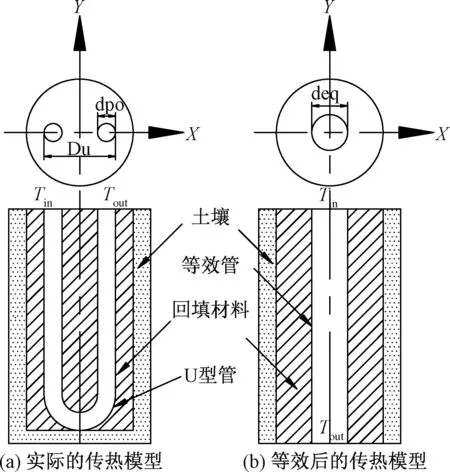
图1 竖直U型地埋管传热模型Fig.1 A transfer model of the buried vertical U-tube

1.2数学模型

1.2.1控制方程

本文基于有限元分析法，采用COMSOL软件进行模拟求解[11]。地埋管附近区域采用加密网格处理，离地埋管较远距离处采用标准网格处理。管内流体流动用到连续、动量方程计算管道中不可压流体的速度、压力[12]：

(2)

(3)

式中：u——等效管横截面流体的平均速度/(m·s-1)；

ρ——流体的密度/(kg·m-3)；

p——压力水头/m。

dh=4A/Z

式中：Re——雷诺数；

μ——流体的黏性系数/(N·s·m-2)；

e——U型管内表面粗糙系数/mm；

F——质量力/(N·kg-1)；

dh——当量管直径/m；

A——当量管横截面积/m2；

Z——当量管湿周/m。

管道内流体传热过程所用到的热平衡方程：

(4)

Qwall=(hZ)eff(Text-T)

式中：Cp——比热容/(J·kg-1·℃-1)；

k——导热系数/(W·m-1·℃-1)；

Q——广义热源/W；

Qwall——通过管壁的换热量/W；

(hZ)eff——对流换热系数h与管壁截面周长乘积的有效值；

Text——管壁外侧土壤的温度/ ℃。

式(4)右边第二项为黏性剪切所产生的热量。

土壤导热微分方程[13]：

(5)

式中：ρe——多孔土壤的密度；

ce——多孔土壤的定压比热容；

λe——多孔土壤的导热系数。

ρe=ερ1+(1-ε)ρs

(6)

ce=εc1+(1-ε)cs

(7)

λe=ελ1+(1-ε)λs

(8)

式中：ε——土壤的孔隙率，本文中源项S等于0。

1.2.2初始条件与边界条件

(1)初始条件：

Tin=Tout=Tp=T0τ=0

(9)

(2)边界条件：

①土壤无穷远处边界条件为：

T(x，y，z，τ)=T0

(10)

②地表与底部土壤边界条件为：

(11)

③流体入口处边界条件为：

Tin(z,τ)|z=0=Tf(τ)

(12)

④U地埋管内壁与流体的边界条件为热泵运行时：

(13)

热泵停止时：

h=0

(14)

⑤管外壁与土壤接触面处的边界条件为：

Tp(z,τ)|r=rout=Ts(z,τ)|r=rout

(15)

⑥单位井深换热量为：

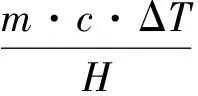
(16)

式中：T0——土壤初始温度/℃；

Tp——竖直U型地埋管初始温度/℃；

Tf(τ)——不同时刻下地埋管入口水温/℃；

h——管内流体对流换热系数/(W·m-2·℃-1)；

q——单位井深换热量/(W·m-1)；

m——入口流体质量流量/(kg·s-1)；

c——流体定压比热容/(J·kg-1·℃-1)；

ΔT——地埋管入、出口温差/℃；

H——钻井深度/m；

rin、rout——当量直径单管内、外径/m。

2 模型的试验验证

利用本文建立的模型对文献[14]中的试验进行模拟，以验证模型的准确性。模拟值与试验值的对比结果见图2、3。图2为热泵连续蓄热60天过程中，埋管进、出口温度随运行时间的变化规律。

从图2可以看出，地埋管进口温度模拟值保持不变，实验测试值曲线围绕模拟值上下做微小波动。地埋管出口温度测试值变化范围较大，且模拟值在热泵运行5天后几乎保持不变，分析可知试验测试值波动较大是因为热泵实际运行过程中受气候条件等因素影响较大，而模拟值则因所建模型边界条件较为理想，所以模拟值的规律性较好且波动浮动较小。

图2 实验测试值与模拟值对比结果Fig.2 Comparison of the calculated and experimental values

图3分析了地埋管出口水温实验测试值与模拟值之间的相对误差，可以看出相对误差最大为0.14%，最小误差为0.01%。在实际工程中以上误差均在允许范围以内，因此本文所建传热模型能够较好地研究热泵实际运行过程中地埋管换热器与土壤之间的传热规律。

图3 误差分析结果Fig.3 Comparison results of errors

3 不同因素对地埋传热规律的影响

3.1计算参数

表1和表2均为内蒙中部地区某地源热泵设计过程中所用到的技术参数及地质参数资料[15]。

表1 计算参数Table 1 Calculation parameters

3.2土壤结构的影响

对内蒙中部地区土壤结构进行分析得出地表以下0～12 m土壤主要由砂质、黏土和砾砂组成； 12～40 m由中粗砂和卵砾石层组成； 40～100 m以中粗砂、黏土和粉质黏土为主。由于不同深度范围之间的土壤热物性参数差异较大，因此人为的将以上三种不同深度范围之间的土壤分为上、中、下三层，物性参数见表2。

表2 地下土壤结构Table 2 Subsoil structure

注：λ为导热系数/(W·(m·℃)-1)；Cp为比热容/(J·(kg·℃)-1)；ρ为密度/(kg·m-3)。

研究结果见图4。从图4(a)可以看出，径向距离(r=0.5 m)一定时，不同层土壤温度均随运行时间的增加而升高，涨幅依次为中层、下层、上层。图4 b反映了土壤结构对热作用半径的影响规律，可以看出随着运行时间的增加，热作用半径逐渐增加且趋于稳定，中层最大，上层和下层次之。结合表2中的数据可知，三层土壤导热系数大小依次为，中层>上层>下层；而热扩散系数大小依次为中层(6.83×10-7m2/s)>下层(3.33×10-7m2/s)>上层(2.27×10-7m2/s)。因此，热量在土壤中的传递速率大小取决于土壤热扩散系数的大小。在运行时间一定时，热扩散率越大热量在土壤中的传递速率越快且热作用半径也较大，反之亦然。

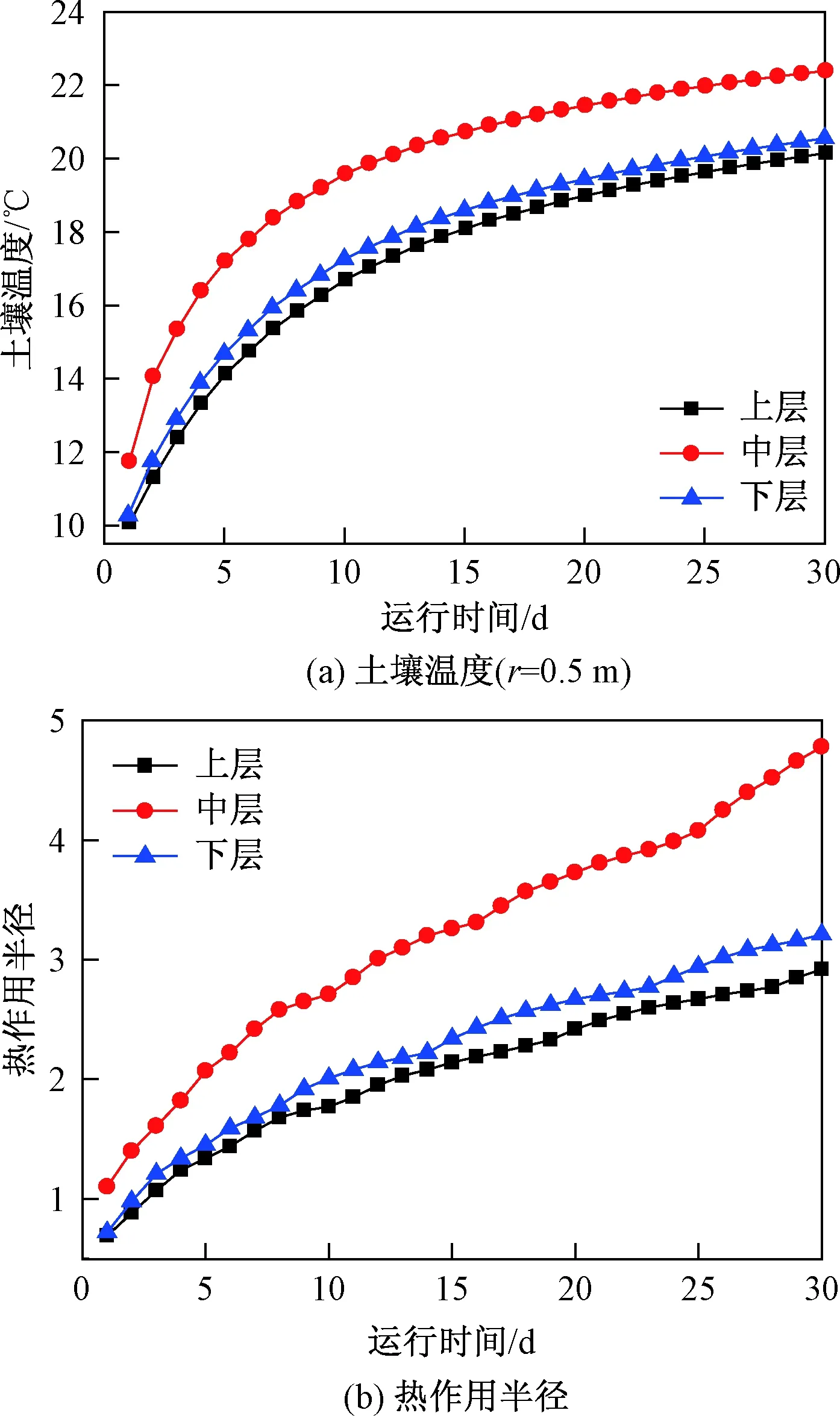
图4 土壤结构对地埋管传热规律的影响Fig.4 Effects of subsoil structure on heat transfer characteristics of the buried pipe

3.3入口水温的影响

为探究入口水温对地埋管传热规律的影响。图5 分别给出了不同入口水温对地埋管出口温度及单位井深换热量的影响(质量流量为1.13 kg/s)。从图5可以看出，当流体入口温度为30、40、50和60 ℃时，地埋管散热48 h后，对应的出口温度分别为29.38、39.05、48.78和58.46 ℃，相应的入、出口温差依次为0.62、0.95、1.22、1.54 ℃；其对应的单位井深换热量依次为29.4、43.7、57.9和73.1 W/m。

分析可知，流体入口温度增加时，地埋管换热器与周围土壤之间的温差增大温度梯度增加，单位井深换热量增加。因此，在流体入口质量流量保持不变的情况下，增加入口水温有利于地埋管入、出口温差及单位井深换热量的增加。综上分析，在地埋管材质温度变形范围内，热泵运行过程中，应适当提高流体入口温度，从而达到增加单位井深换热量，提升土壤蓄热量的目的，这对于改善内蒙地区土壤热失衡问题具有重要意义。

图5 埋管出口水温和单位井深换热量随入口水温的变化规律Fig.5 Dynamic changes in the outlet water temperature and the transfer rate per unit borehole depth with different inlet water temperatures

3.4质量流量的影响

进入地埋管中水的质量流量不同，会对地埋管进出口温差及单位井深换热产生影响。图6 分别给出了地埋管进出口温差及单位井深换热量随热泵运行时间的变化规律(入口水温为40 ℃)。图6(a)可以看出地埋管进出口温差随流体质量流量的增加而减小，这是由于流体质量流量越小流动过程中在地埋管中停留的时间长与土壤发生热交换较充分，温度下降程度较大；而流体质量流量越大时，在地埋管中停留的时间较短，且不能与地埋管周围土壤充分换热，因此温差较小。

图6(a)显示了流体质量流量为1.13、1.69、2.26和2.83 kg/s时，地埋管散热48 h后对应的进出口温差分别为0.92、0.61、0.47和0.38 ℃。从图6(b)可以看出，三种不同质量流量下地埋管散热48 h后，单位井深换热量基本相等。结合式(16)可知，单位井深换热量主要取决于流体质量流量和地埋管进出温差；而质量流量小的情况下进出口温差较大,质量流量大的情况下进出口温差较小，单位井深换热量由二者共同决定。对图6(b)曲线分析可知四种质量流量下单位井深换热量基本相等。从热泵运行18～48 h可以看出，流体质量流量大的换热量相比质量流量小的换热量有所升高，也就是说随着热泵运行时间的增加流体质量流量相对入、出口温差占主导因素。在本文的研究条件下地埋管入口流体质量流量宜取1.13～1.69 kg/s，过大会导致循环水泵功率的增加。

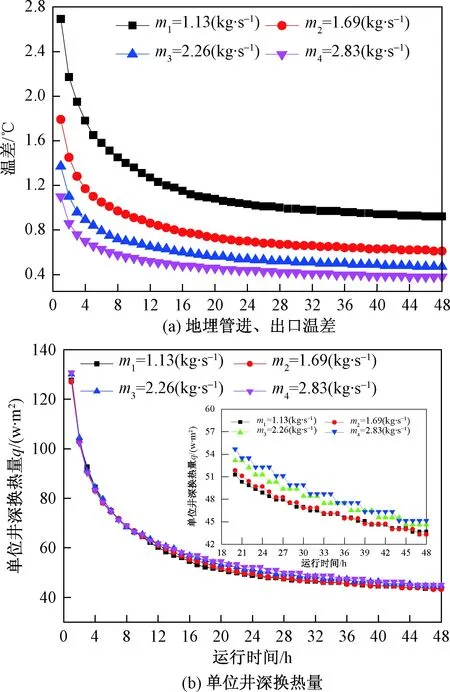
图6 不同质量流量下进出口温差及单位井深换热量的变化规律Fig.6 Outlet water temperature difference and transfer rate per unit borehole depth with different mass fluxes

3.5热泵运行模式的影响

热泵在实际运行过程中，涉及到连续运行和间歇运行两种模式。以下主要分析了两种运行模式对土壤温度场及单位井深换热量的影响。

图7反映了热泵间歇(开机1 h，停机1 h)运行模式下，径向距离(r=0.08 m)相等的情况下，不同层土壤温度场的变化规律。可以看出，三层土壤温度均出现波动式上升，上层土壤温度最高、中层次之、下层最低，这是因为蓄热过程中流体首先经过上层土壤，与其进行热交换后再与中层及下层土壤热交换。

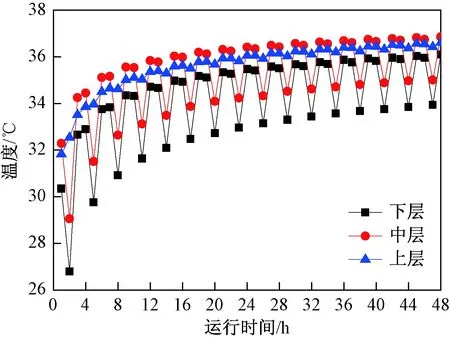
图7 间歇模式土壤温度Fig.7 Soil temperature of the intermittent operation

图8分别给出了两种模式下同一深度(H=80 m)处，不同径向距离处土壤温度的变化规律。从图8(a)可以看出，间歇运行模式下土壤温度随着径向距离的增加波动幅度逐渐降低。当r=0.3 m时，土壤温度波动幅度与连续运行模式一致。图8(b)反映了热泵连续运行模式下，土壤温度场的变化规律。可以看出，不同半径处，土壤温度均随热泵运行时间的增加而升高，离地埋管越近土壤温度越高，但趋于稳定，整个运行过程中土壤温度未出现过上下波动的现象。分析可知热泵连续运行模式下热量是连续传递的，因此未出现温度的波动。

图8 两种模式下土壤温度的变化Fig.8 Changes in soil temperature of two models

图9给出了两种运行模式下，单位井深换热量随时间的变化规律。可以看出，连续运行模式下单位井深换热量，先下降后保持不变；而间歇模式下单位井深换热量，先升高后下降再升高，这样周期性的变化。从热泵运行效率方面来讲，间歇模式增加了地埋管中热量散失的时间，土壤温升率处于较低范围，同时降低了循环水泵的功率，提高了地埋管的换热效率及系统COP。因此，在满足系统负荷的前提下，应采用间歇运行模式。

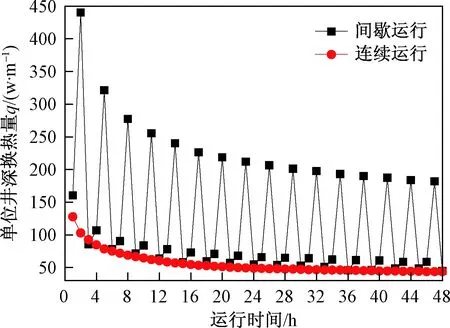
图9 单位井深换热量Fig.9 Transfer rate per unit borehole depth

4 全年蓄热-恢复-取热过程

跨季节蓄热型热泵系统对于解决土壤热失衡问题具有重要指导意义。以下主要研究了蓄热型地源热泵系统全年运行过程中，地埋管周围土壤温度场的变化规律。同时，依据内蒙中部地区全年气候特点，以热泵运行一年为周期，对内蒙中部地区蓄热型热泵系统运行过程中，土壤温度变化进行动态模拟。本文选取运行模式为，夏季蓄热3个月，春秋季恢复3个月，冬季取热6个月，从而实现热泵全年运行。

由图10 可知，全年运行过程中不同半径处土壤温度随热泵蓄热、恢复及取热时间的不同，均呈现出上升、缓慢下降和下降的变化规律。由图10可知蓄热型热泵经历一个运行周期后，径向距离为0.5、0.8、1.0及1.5 m处土壤温度分别为8.16、9.29、9.6和10.16 ℃，可以看出随径向距离的增加土壤温度逐渐升高。

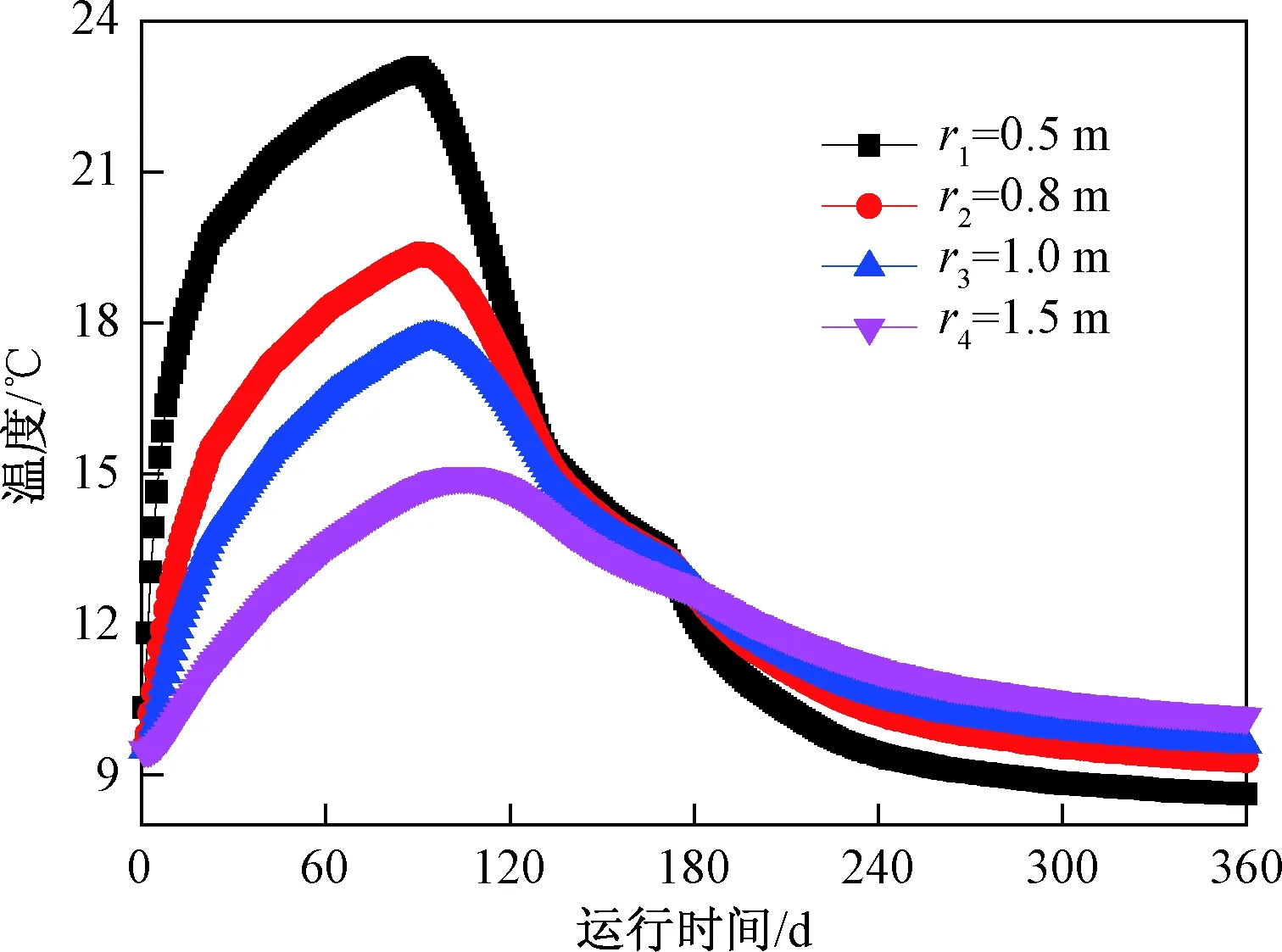
图10 不同半径处土壤温度的变化Fig.10 Changes in soil temperature at different radius

图11(a)给出了不同蓄热流体温度对径向距离(r=0.5 m)处土壤温度的影响。可以看出随着蓄热流体温度的提高，土壤温度逐渐升高；进一步分析可知当蓄热流体温度为40、50、60 ℃时对应的全年土壤温升分别为-1.34、3.93、8.72 ℃，也就是说对于蓄热流体温度为40 ℃时，经过一个运行周期后，土壤温度相对初始温度而言依然在下降，从解决土壤热失衡问题看，蓄热过程中流体温度不宜小于40 ℃具体应该结合实际工程热负荷而定。

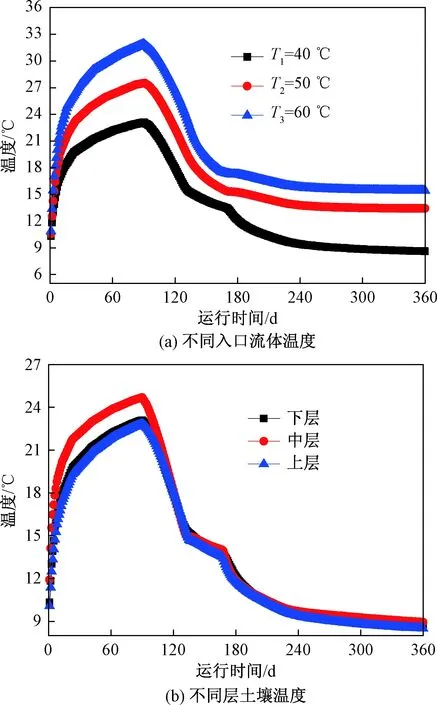
图11 土壤温度随时间的变化(r=0.5 m)Fig.11 Changes in soil temperature at r=0.5 m with the operation time

图11(b)为不同层土壤径向(r=0.5 m)处土壤温度随热泵运行时间的变化规律，可以看出中层土壤温升率较大且温度下降也较快，而上层和下层基本一致，这主要是因为中层土壤热扩散率较大，热作用半径也较大，在相同时间及相同的半径处其温升也较大。从蓄热的角度分析，上层和下层土壤适合作为蓄热材料，而中层土壤宜作为回填材料。

5 结论

(1)蓄热过程中，土壤热作用半径及土壤温度随热泵运行时间的增加而增大，且土壤热扩散率越大热量传递增幅越大。

(2)单位井深换热量取决于流体进出口温差和流体质量流量两个因素，且流体质量流量占主导因素。

(3)相比连续运行模式，间歇运行过程中地埋管附近土壤温度呈波动变化且土壤温升率较低，从而提高了热泵机组运行效率、地埋管换热量及热泵对浅层地热资源的利用率。

(4)跨季节蓄热型地源热泵系统能够较好地改善内蒙中部地区土壤热失衡问题。土壤热失衡改善效果随蓄热流体温度的提高而增加，从热泵全年运行考虑，蓄热期流体入口温度不应低于40 ℃。

[1] 刘爱华, 佟红兵, 冉伟彦. 北京某垂直地埋管区低温场变化规律研究[J]. 水文地质工程地质,2016, 43(4):165-170.[LIU A H，TONG H B，RAN W Y. A study of ground temperature changes in a vertical heat exchanger area of Beijing[J]. Hydrogeology & Engineering Geology, 2016,43(4):165-170.(in Chinese)]

[2] 王勇, 尹畅昱, 金逸韬. 基于岩土失调温度限值的土壤源热泵系统土壤蓄能状态评价[J]. 湖南大学学报(自然科学版), 2015, 42(1):127-135.[WANG Y, YIN C Y, JIN Y T. Evaluation of the ground energy storage condition of ground source heat pump system based on energy storage imbalance temperture limit[J]. Journal of Hunan University(Natural Sciences)2015, 42 (1):127-135.(in Chinese)]

[3] 杨卫波, 施明恒, 陈振乾.非连续运行工况下垂直地埋管换热器的换热特性[J]. 东南大学学报(自然科学版), 2013, 43(2):328-333.[YANG W B, SHI M H, CHEN Z Q. Heat exchange characteristics of vertical U-tube ground heat exchanger with discontinuous operation condition[J]. Journal of Southeast University (Natural Science Edition), 2013, 43(2):328-333.(in Chinese)]

[4] 李新国, 胡晓辰, 王健. 太阳能、蓄热与地源热泵组合系统能量分析与实验[J]. 太阳能学报, 2012, 33(4):640-646.[LI X G, HU X C, WANG J. Energy analyses and experiment on solar-ground coupled heat pump with seasonal storage system[J]. Acta Energiae Solaris Sinica, 2012, 33(4):640-646.(in Chinese)]

[5] 王芳, 郑茂余,李忠建,等. 相变材料在太阳能-地源热泵系统中的应用[J].太阳能学报, 2006, 27(12):1231-1234.[WANG F, ZHENG M Y, LI Z J,etal. Application of phase change material in solar assisted ground-source heat pump system[J]. Acta Energiae Solaris Sinica, 2006, 27 (12):1231-1234. (in Chinese)]

[6] Tian B W. A new solution for underground thermal imbalance of ground-coupled heat pump systems in cold regions: Heat compensation unit with thermo-syphon[J]. Applied Thermal Engineering, 2014, 64 (14):283-292.

[7] Yang W B. Numerical investigation on the underground thermal imbalance of ground-coupled heat pump operated in cooling-dominated district[J]. Applied Thermal Engineering, 2013, 58(13):626-637.

[8] You T, Wang B, Wu W,etal. A new solution for underground thermal imbalance of ground-coupled heat pump systems in cold regions: Heat compensation unit with thermosyphon[J]. Applied Thermal Engineering, 2014, 64(Supp1/2):283-292.

[9] Rabin Y, Korin E. Incorporation of phase-cange materials into a ground thermal energy storage system: theoretical stydy[J]. Journal of Energy Resources Technology, 1996, 118(3):237-241.

[10] Gu Yian, O Neal Denni L. Development of equivalent diameter expression for vertical U-tubes used in ground-coupled heat pumps[J]. Ashrae Transactions, 1998, 104(2):347-355.

[11] Stepan Ozana, Martin Pies, Tomas Docekal. Case studies on optimization problems in MATLAB and COMSOL multiphysics by means of the livelink[J]. Aip Conference Proceedings, 2016, 1738(1):571-578.

[12] 林瑞泰.多空介质传热传质引论[M]. 北京:北京科技出版社, 1995.[LIN R T. An introduction to heat and mass transfer in porous media[M]. Beijing: Beijing science and Technology Publishing House,1995. (in Chinese)]

[13] 陶文铨.数值传热学[M]. 2版.西安:西安交通大学出版社, 2001.[TAO W Q. Numerical heat transfer[M]. 2nd ed. Xi’an: Xi’an Jiao Tong University press, 2001. (in Chinese)]

[14] 高蓬辉, 纪绍斌, 周国庆，等. 地层储放能过程中温度场演化规律的试验研究[J]. 太阳能学报, 2013, 34(11):1916-1923.[GAO P H, JI S B, ZHOU G Q,etal. Experimental research on temperature of underground soil in the process of storage and release[J]. Acta Energiae Solaris Sinica, 2013, 34(11):1916-1923. (in Chinese)]

[15] 张永志, 顾洁. 内蒙古中部地区地源热泵单位井深换热量设计的研究[J]. 建筑节能, 2012, 256 (40):24-25.[ZHANG Y Z, GU J. Designing of Average Quantity of Heat Per Meter for Ground Source Heat Pump at central Inner Mongolia[J].Building Energy Efficiency, 2012, 256 (40):24-25. (in Chinese)]

责任编辑：张若琳

Astudyoftheheattransferlawofgroundsourceheatpumpwithseasonalheatstorage

WU Xuan1, LU Ziye1, LIU Wei1, LIANG Panlong1, TIAN Xuekai2, JIN Guang1

(1.SchoolofEnergyandEnvironment,InnerMongoliaUniversityofScienceandTechnology,Baotou,InnerMongolia014010,China; 2.CollegeofPipelineandCivilEngineering,ChinaUniversityofPetroleum(EastChina),Qingdao,Shandong266580,China)

Based on the method of finite element analyses a quasi 3-D unsteady-state heat transfer model was developed. Changes in soil temperature, transfer rate per unit borehole depth and thermal influencing radius for ground source heat pump with seasonal heat storage with the heat pumps operation time were analyzed by comparison with the experimental results. The effects of soil structure, inlet water temperature, inlet mass flux and operation models on heat transfer of soil and the issue of ground heat balance were investigated. The results indicate that soil temperature at the same radius of different depths increases with the soil thermal diffusivity, the thermal influencing radius increases with the operation time, and the inlet water temperature gradually tends to be steady. The fluctuation changes in the soil temperature and heat transfer rate under the intermittent operation model and the soil temperature of radial distance more than 0.3 m were fitted with two models, indicating that the mass flow rate of the inlet fluid was not too big under the requirement of the heat transfer rate of the system, the soil temperature is recovered after one cycle of operation (360 d) of the ground source heat pump system with seasonal heat storage, and the fluid inlet temperature should be more than 40 ℃.

ground source heat pump; buried pipe; thermal influencing radius; operation mode; ground heat balance

P314.1

A

1000-3665(2017)05-0164-08

金光(1970-)，女，博士，教授，从事热过程节能减排、新能源应用技术。E-mail:13772403854@163.com

10.16030/j.cnki.issn.1000-3665.2017.05.25

2016-07-12;

2016-08-10

内蒙古自治区科技创新引导奖励资助项目(2017CXYD-1)；内蒙古自治区自然科学基金资助项目(2015MS0561);2017年内蒙古自治区应对气候变化及低碳发展专项资金项目

吴晅(1976-)，男，博士，副教授，从事土壤源热泵技术研究。E-mail:wxgif@163.com