应力历史对弱透水层参数影响试验研究
李兆峰,戴云峰,周志芳,张博然,周翠英
(1.成都理工大学环境与土木工程学院,四川 成都 610059;2.中山大学工学院,广东 广州 510275;3.南京水利科学研究院水文水资源与水利工程科学国家重点实验室,江苏 南京 210029;4.河海大学地球科学与工程学院,江苏 南京 211100)
应力历史对弱透水层参数影响试验研究
李兆峰1,2,戴云峰3,周志芳4,张博然4,周翠英2
(1.成都理工大学环境与土木工程学院,四川 成都 610059;2.中山大学工学院,广东 广州 510275;3.南京水利科学研究院水文水资源与水利工程科学国家重点实验室,江苏 南京 210029;4.河海大学地球科学与工程学院,江苏 南京 211100)
弱透水层储存的地下水是地下水资源的重要组成部分,弱透水层水文地质参数对地下水资源管理与评价以及地面沉降等具有重要意义。通过室内试验对定降深条件下弱透水层水流运移规律进行了研究,并探讨了弱透水层释水过程中的变形规律和释水规律。试验结果表明,在相邻含水层定降深条件下,弱透水层固结变形滞后于相邻含水层的降深变化,且变形速度逐渐变小并趋于零。基于室内试验,利用配线法求得弱透水层不同应力状态下的水文地质参数,对比分析,大变形和小变形试验中土层的渗透系数变化不大,但贮水率明显变小,土层的固结系数变大。因此,土层的应力历史对土层的渗透系数影响不大,而对贮水率有较大的影响。
弱透水层;应力历史;滞后变形;水力参数
弱透水层储存的地下水是地下水资源的重要组成部分,然而在地下水管理和预测中却经常被忽视[1]。近年来,很多水文地质学者关注弱透水层[2~5]。在冲积平原和沉积盆地中弱透水层广泛分布,且主要由黏土、粉质黏土等细粒沉积物组成,具有低渗透性和高储水性的重要性质[6~9]。弱透水层的渗透系数一般小于10-8m/s,比含水层小几个数量级,而其贮水率比承压含水层大得多[10~12]。当抽水含水层水位下降时,水压力下降,有效应力升高,弱透水层储存的地下水释放到相邻含水层,同时弱透水层固结变形,造成地面沉降[13~14]。然而,弱透水层释水变形的大部分为塑性变形,即使含水层系统水位恢复,弱透水层也不会明显回弹,弱透水层水资源量具有不可恢复性[1,7,15]。因此,研究弱透水层水文地质参数的变化规律对地下水资源管理与评价以及地面沉降等都具有重要意义。
弱透水层的水文地质参数包括渗透系数和贮水率,其中渗透系数主要指垂向渗透系数(弱透水层中的水流为垂向的一维流)[16],而贮水率包括弹性贮水率(有效应力小于前期最大固结应力)和非弹性贮水率(有效应力大于最大前期固结应力)[17]。很多水文地质学者对弱透水层水文地质参数进行了大量研究[7,11,18~19]。叶淑君等[19]利用图解法对上海含水层系统中的弱透水层参数进行了研究。Zhou[7]等人提出了配线法求解弱透水层的渗透系数和贮水率,并通过室内试验验证了方法的可靠性。弱透水层应力历史对其参数影响的研究尚未发现。本文通过室内试验对定降深条件下弱透水层的释水变形规律进行研究,并探讨了应力历史对弱透水层参数的影响。
1 原理
Terzaghi一维固结理论在解决软土地基变形控制和预测中发挥着重要的作用,至今仍被广泛应用于计算各种荷载条件下土体的固结问题,如道路、贮油罐、填埋场等地基土的固结沉降计算。为了研究应力历史对弱透水层参数的影响,建立一个含水层系统概念模型如图1所示。假设:(1)弱透水层是均质的,且渗透系数和贮水率不随时间变化;(2)弱透水层水平侧向无限延伸;(3)弱透水层始终是饱和状态;(4)弱透水层中的水流为垂向一维流,且服从达西定律。通常情况下弱透水层的渗透系数比含水层小两个数量级以上,因此,弱透水层中的水流可近似为一维流动。坐标轴原点O位于弱透水层的上表面,厚度为l,坐标z向下为正。建立如下数学模型:
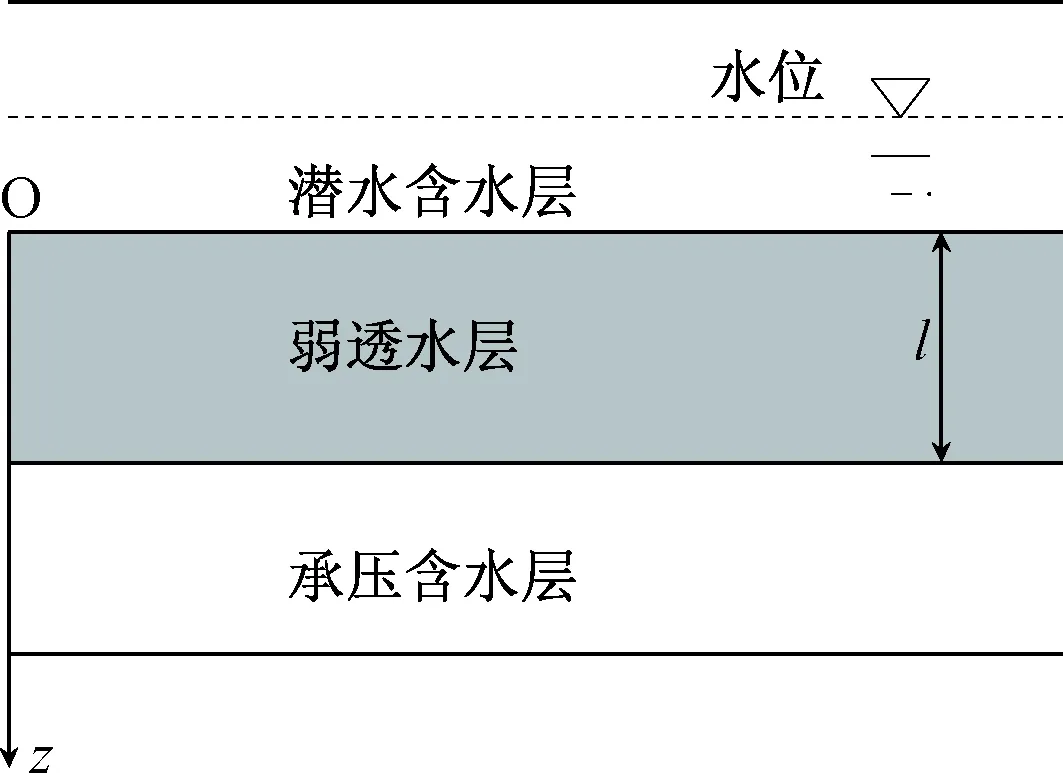
图1 含水层系统概念模型Fig.1 Conceptual model of the aquifer system
式中:cv——弱透水层的固结系数;
kv——渗透系数;
Ss——贮水率;
s——弱透水层内部的降深;
t——时间。
初始时刻土样中的降深为0,土样上边界降深为0,下边界为定降深,即:
式(1)~(4)所示的偏微分方程,利用分离变量法可以求得其解析解[20]。
根据Darcy定律,求得土样中的水流速度,土样底面的水流速度为:
无量纲化:
其中:
将式(7)和式(8)等号两边同时取对数,得:
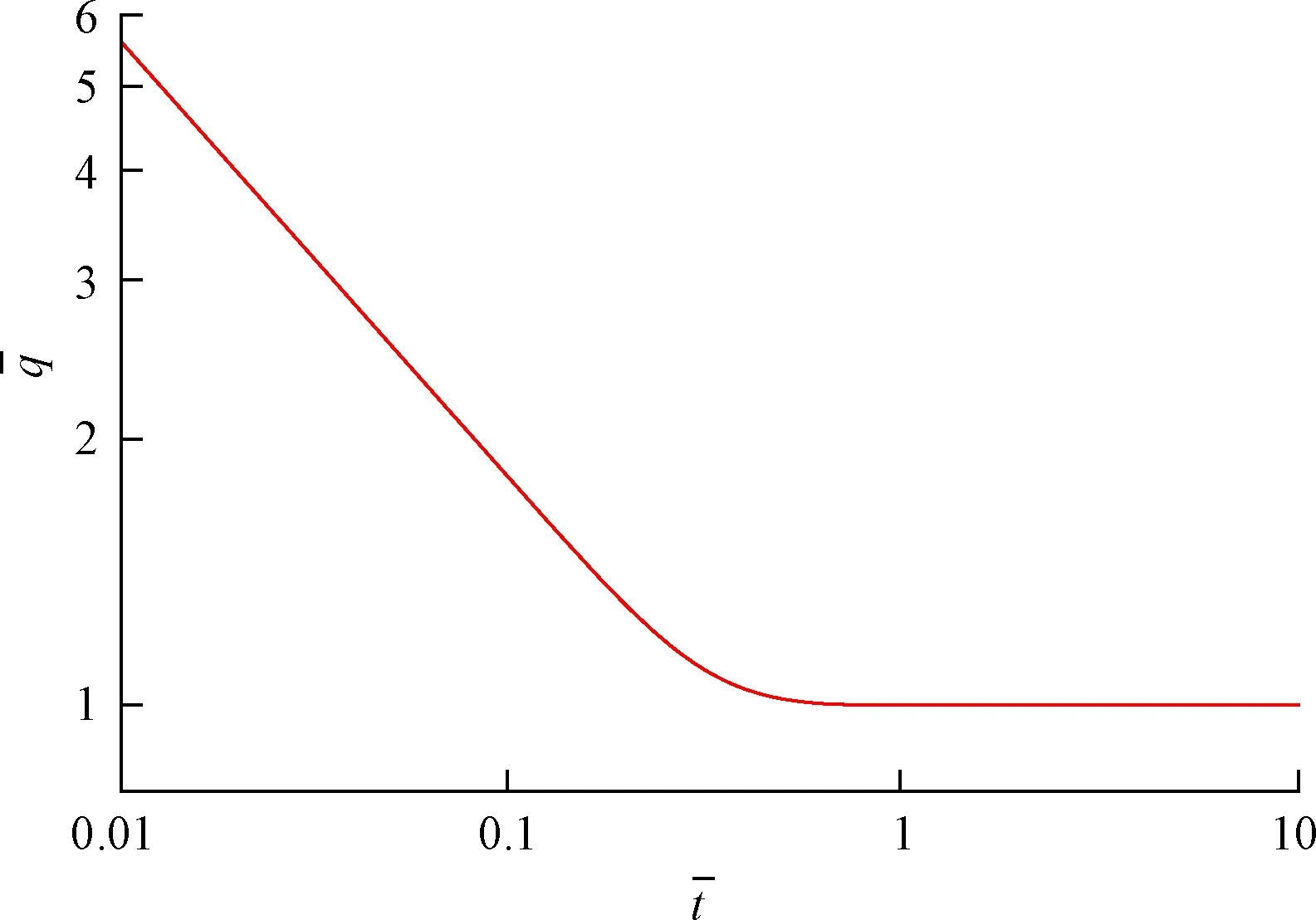
图2 土层底面流量标准曲线Fig.2 Standard curve of flow at the bottom of soil layer
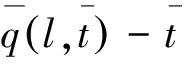
2 试验研究
2.1试验
为了研究弱透水层内部的水流特征,对相邻含水层定降深条件下弱透水层的水流特征、变形和释水规律进行研究。试验装置是在前人试验模型的基础上进行改进,并合理设计符合弱透水层的固结渗流环境。模型由模型主体(外径20 cm、内径19 cm)、沉降量测系统、流量监测系统、供水水槽组成(图3)。模型主体密封,下部为反滤层,中部填充试验用的土层,上部充满水。试验所用土样是从野外取回的粉质黏土,将其风干,碾碎并过筛(0.45 mm)。将制备的土样填充到试验设备的主体部分,试验土样初始时刻厚度l=15.5 cm。试验结束后取多组试样,用环刀法获得试验土层的干密度为1.63×103kg/m3,初始孔隙比e0=1.31。
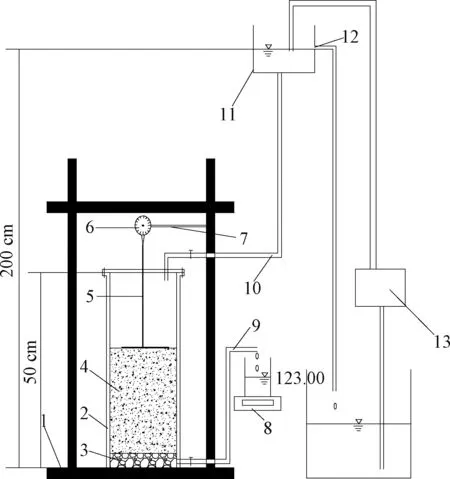
图3 试验模型示意图Fig.3 Schematic diagram of the experimental model1—底座;2—容器主体;3—反滤层;4—黏土层;5—刚性杆;6—百分表;7—支架;8—电子天平;9—出水管;10—进水管;11—定水头供水槽;12—溢水口;13—蠕动泵
本文对同一土层进行了两组定降深条件下的水流运移试验。其中,第二组试验是在第一组试验基础上进行的,且第一组土层变形量比第二组大,故第一组为大变形试验,试验开始前土层属于正常固结土;第二组为小变形试验,试验开始前土层处于超固结状态。第一组试验开始前弱透水层上下两端水头相等,试验初始时刻打开下部出水口阀门,将下部反滤层水头突然降低ΔH=150 cm,并保持不变,持续观测下部出水口处的流量和土层的变形量,待出水口流量达到稳定(此过程为大变形试验)。关闭出水口阀门,此时土层开始发生回弹变形,持续观测百分表读数,待百分表读数稳定,即土层回弹变形结束。土层回弹变形稳定后,试验土层厚度l=14 cm,此时可以进行第二组试验。与第一组试验步骤相同,试验开始时刻将下部反滤层水头突然降低ΔH=150 cm,并保持不变,持续观测下部出水口处的流量和土层的变形量,待出水口流量达到稳定(此过程为小变形试验)。土层底面流量记录的数据为某一时刻t时,出水口总出水量q。假设过水断面面积为A,t1时刻总水量为q1,t2时刻总出水量为q2;则计算所得(t1+t2)/2时刻的瞬时流量为(q2-q1)/A(t2-t1)(表1、表2)。
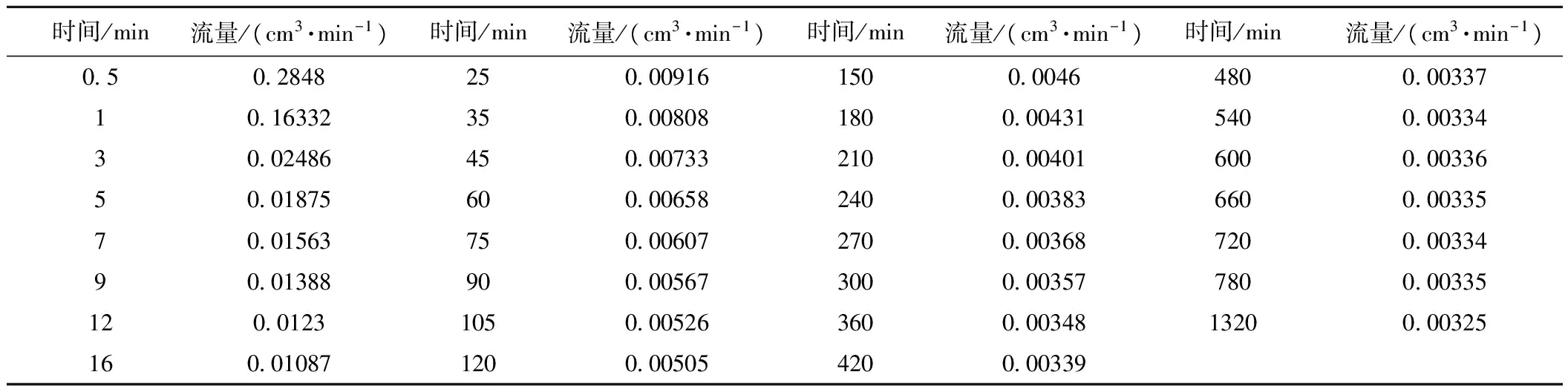
表1 大变形试验土层底面流量

表2 小变形试验土层底面流量
2.2试验结果分析
两次试验的土层累积变形曲线如图4所示。试验结果表明,在两次定降深条件下水流运移试验中,土层的变形规律是相同的,初始时刻变形较快,随后变形速度逐渐减小并趋于稳定,土体的变形较相邻含水层的降深存在滞后现象。在降深相同的条件下,第一次试验中土样的总变形量要比第二次试验大,即大变形试验土层释水量比小变形试验大,说明试验土层贮水率与土层的固结历史有关。
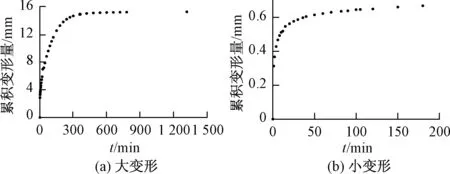
图4 土层累积变形量Fig.4 Cumulative deformation of soil layer
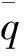
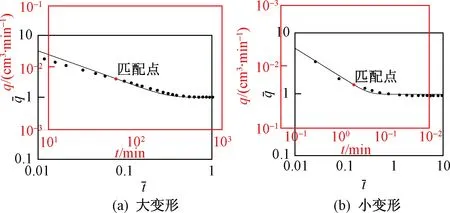
图5 土层底面流量配线求参数Fig.5 Parameter determination with flow at the bottom of soil layer

[q][t][q][t]6582×10-3cm3/min60min2008
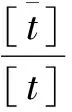

表4 小变形时匹配点坐标
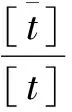
计算结果表明,大变形和小变形试验土层的固结系数分别为9.7和0.26 cm2/min,土层大变形和小变形试验中滞后释水现象的滞后因子(τ0=l2/cv)分别为750和20,即土层大变形试验和小变形试验的释水现象分别在750 min和20 min时基本结束,土层内部的水流由非稳定流变为稳定流。因此,土层大变形试验的滞后因子较大,滞后释水现象所需时间较长。计算结果与试验结果一致。
大变形试验和小变形试验分别取试验开始750 min和20 min之后的土层底面流量,利用Darcy定律,计算土层的渗透系数分别为3.11×10-4、3.09×10-4cm/min,两次试验的计算结果和利用配线法获得的参数基本相同,说明利用配线法计算弱透水层渗透系数的精确性。利用配线法获得大变形和小变形试验土层的渗透系数均为3.1×10-4cm/min,通过对比分析,利用配线法获得的渗透系数与土层内部水流稳定(即土层变形结束)时的渗透系数相同。土的渗透性与土层孔隙比关系密切。土层初始孔隙比e0=1.31,大变形和小变形试验结束后土层对应的孔隙比分别为1.09和1.07,弱透水层的渗透系数随土层的孔隙比减小而非线性减小,由于两次试验结束时孔隙比变化不大,因此两次试验所求渗透系数基本相同是合理的。
小变形试验时土层的贮水率比大变形试验变小,且变化显著。对比分析可知,利用配线法获得土层的贮水率是土层固结引起的总释水量(即总变形量)的反映。大变形试验开始前土层属于正常固结土,而小变形试验开始前土层的前期固结压力大于现有的有效应力水平,土层处于超固结状态。试验结果表明,相同应力条件下,土层在超固结状态时的变形量比正常固结状态小。土层小变形试验是在大变形试验的基础上进行的,因此土层的应力历史对土层的渗透系数影响不大,而对土层的贮水率有较大的影响。
2.3验证
将利用配线法求得的土层水文地质参数代入式(6),计算得到土层底面的流量曲线和试验结果进行对比。图6分别为土层大变形和小变形试验时土层底面流量的实测值和计算值。对比可知,实测值和计算值一致,说明利用配线法求得的土层参数能很好地反映土层固结变形过程中的水流运动规律。
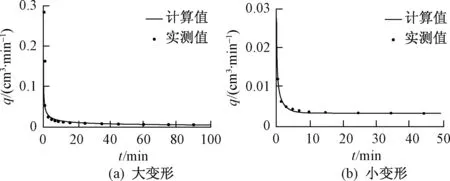
图6 土层底面流量Fig.6 Flow at the bottom of soil layer
3 结论
(1)弱透水层固结变形滞后于相邻含水层的降深变化,在相邻含水层定降深条件下,弱透水层的释水和变形速度由大变小并趋于零,验证了弱透水层滞后释水现象的存在。
(2)通过大、小变形试验对比可知,大变形试验的滞后释水现象时间较长,两次试验中土层的渗透系数变化不大,贮水率明显变小,固结系数变大。因此,弱透水层应力历史对其渗透系数影响不大,而对贮水率有较大影响。
研究成果对地面沉降和弱透水层释水量的计算具有一定的应用价值。本文未考虑弱透水层固结过程中水文地质参数的变化,需作进一步的研究。
[1] Konikow L F, Neuzil C E. A Method to Estimate Groundwater Depletion from Confining Layers[J]. Water Resources Research, 2007, 43(7): 931-936.
[2] 张云, 薛禹群, 吴吉春,等. 饱和黏性土蠕变变形试验研究[J]. 岩土力学, 2011, 32(3): 672-676.[ZHANG Y, XUE Y Q, WU J C,etal. Experimental study of creep deformation of saturated clay[J]. Rock and Soil Mechanics, 2011, 32(3): 672-676. (in Chinese)]
[3] 宋爽, 李绪谦, 冷菁, 等. 弱透水层中有机污染物(菲)的衰减研究[J]. 水文地质工程地质, 2011, 38(4): 111-116.[SONG S, LI X Q, LENG Q,etal. A study of the attenuation of the organic pollutant (phenanthrene) in an aquitard[J]. Hydrogeology & Engineering Geology, 2011, 38(4):111-116. (in Chinese)]
[4] 李静,梁杏,靳孟贵. 低渗透介质孔隙溶液的提取及其应用综述[J]. 水文地质工程地质, 2012, 39(4): 26-31.[LI J, LIANG X, JIN M G. Review on pore water extraction techniques in low-permeability media and their application[J]. Hydrogeology & Engineering Geology, 2012, 39(4): 26-31. (in Chinese)]
[5] 叶淑君,戴水汉. 地下水流二维、准三维及三维模型模拟结果比较[J]. 水文地质工程地质, 2003, 30(5): 23-27.[YE S J, DAI S H. Comparing of results of two dimensional, quasi three dimensional and three dimensional models for groundwater[J]. Hydrogeology & Engineering Geology, 2003, 30(5): 23-27. (in Chinese)]
[6] XUE Y Q, ZHANG Y, YE S J,etal. Land Subsidence in China[J]. Environmental Geology, 2005, 48(6): 713-720.
[7] Zhou Z F, Guo Q N, Dou Z. Delayed Drainage of Aquitard in Response to Sudden Change in Groundwater Level in Adjacent Confined Aquifer: Analytical and Experimental Studies[J]. Chinese Science Bulletin, 2013, 58(25): 3060-3069.
[8] Neuzil C E. Groundwater Flow in Low-Permeability Environments[J]. Water Resources Research, 1986, 22(8): 1163-1195.
[9] Yan X P, Kerrich R,Hendry M J. Distribution of the Rare Earth Elements in Porewaters from a Clay-Rich Aquitard Sequence, Saskatchewan, Canada[J]. Chemical Geology, 2001, 176(1/4): 151-172.
[10] Li Z,Zhou Z. An Analytical Solution for Leakage Rate and Depletion of Aquitard Influenced by the Delayed Yield Phenomenon[J]. Environmental Earth Sciences, 2015, 74(2): 1227-1234.
[11] Zhuang C, Zhou Z F, Zhan H B,etal. A New Type Curve Method for Estimating Aquitard Hydraulic Parameters in a Multi-Layered Aquifer System[J]. Journal of Hydrology, 2015, 527: 212-220.
[12] Neuzil C E. How Permeable Are Clays and Shales?[J]. Water Resources Research, 1994, 30(2): 145-150.
[13] Shi X Q, Xue Y Q, Ye S J,etal. Characterization of Land Subsidence Induced by Groundwater Withdrawals in Su-Xi-Chang Area, China[J]. Environmental Geology, 2007, 52(1): 27-40.
[14] Wu J, Shi X, Xue Y,etal. The Development and Control of the Land Subsidence in the Yangtze Delta, China[J]. Environmental Geology, 2008, 55(8): 1725-1735.
[15] 周志芳, 郑虎, 庄超. 论地下水资源的永久性消耗量[J]. 水利学报, 2014(12): 1458-1463.[ZHOU Z F, ZHENG H, ZHUANG C. Study on the unrecoverable depletion of groundwater resource[J].Journal of Hydraulic Engeering, 2014(12): 1458-1463. (in Chinese)]
[16] Neuman S P,Witherspoon P A. Theory of Flow in a Confined Two Aquifer System[J]. Water Resources Research, 1969, 5(4): 803-816.
[17] Helm D C. One-Dimensional Simulation of Aquifer System Compaction near Pixley, California, I: Constant Parameters[J]. Water Resources Research, 1975, 11(3): 465-478.
[18] Neuman S P, D A. Gardner. Determination of Aquitard/Aquiclude Hydraulic Properties from Arbitrary Water-Level Fluctuations by Deconvolution[J]. Ground Water, 1989, 27(1): 66-76.
[19] 叶淑君,薛禹群. 应用沉降和水位数据计算上海地区弱透水层的参数[J]. 岩土力学, 2005, 26(2): 256-260.[YE S J, XUE Y Q. Stress-strain analysis for storage coefficients and vertical hydraulic conductivities of aquitards in Shanghai area[J]. Rock and Soil Mechanics, 2005, 26(2): 256-260. (in Chinese)]
[20] ZHOU Z F, WANG J G, HUANG Y,etal. Conceptual Data Model and Method of Settlement Calculation for Deformation and Water Release from Saturated Soft Soil[J]. Environmental Earth Sciences, 2014, 71(9): 4235-4245.
[21] 周志芳,徐海洋. 一种实验确定弱透水层水文地质参数的原理与方法[J]. 水文地质工程地质, 2014, 41(5): 1-4.[ZHOU Z F, XU H Y. Theory and methods for determining hydrogeological parameters of an aquitard based on experimental data[J]. Hydrogeology & Engineering Geology, 2014, 41(5):1-4. (in Chinese)]
责任编辑:张若琳
Anexperimentalstudyoftheinfluenceofstresshistoryonparametersofanaquitard
LI Zhaofeng1,2, Dai Yunfeng3, ZHOU Zhifang4, ZHANG Boran4, ZHOU Cuiying2
(1.CollegeofEnvironmentandCivilEngineering,ChengduUniversityofTechnology,Chengdu,Sichuan610059,China; 2.SchoolofEngineering,SunYat-senUniversity,Guangzhou,Guangdong510275,China; 3.StateKeyLaboratoryofHydrology-waterResourcesandHydraulicEngineering,NanjingHydraulicResearchInstitute,Nanjing,Jiangsu210029,China; 4.SchoolofEarthScienceandEngineering,HohaiUniversity,Nanjing,Jiangsu211100,China)
The water in aquitards is an important part of groundwater resources. It is of important significance to determine hydrogeological parameters of an aquitard for the management and evaluation of groundwater resources and for land subsidence. This paper examined the law of the water flow in the aquitard with laboratory test and discussed the law of depletion and deformation of the aquitard when water is released from the aquitard. The results show that the consolidation of the aquitard lags behind the drawdown change of the adjacent aquifer. The deformation rate of the aquitard becomes smaller and tends to zeros under the condition of a constant drawdown of the adjacent aquifer. Based on the results of the laboratory test, the hydrogeological parameters of the aquitard were calculated by using the type curve method under different stress histories. The results suggest that the coefficient of permeability changes little, the specific storativity changes greatly and the consolidation coefficient of the soil layer becomes larger in the large deformation and small deformation tests. The small deformation test is carried out on the basis of the large deformation test of the soil layer. The stress history of the soil layer has little effect on the coefficient of permeability of the soil layer, but has a great influence on the specific storativity.
aquitard; stress history; delayed deformation; hydraulic parameters
P641.2
A
1000-3665(2017)05-0014-06
10.16030/j.cnki.issn.1000-3665.2017.05.03
2016-06-14;
2016-09-15
国家自然科学基金项目(4170225、41572209、51709186);中国博士后科学基金资助项目(2017M611863)
李兆峰(1987-),男,博士,主要从事地质资源与地质工程。E-mail: lizhfzx@gmail.com

