基于EnKF综合水头和浓度观测数据推估地下水流模型参数

兰 天，康学远，施小清，吴吉春

(南京大学地球科学与工程学院/表生地球化学教育部重点实验室，江苏 南京 210023)

基于EnKF综合水头和浓度观测数据推估地下水流模型参数

兰 天，康学远，施小清，吴吉春

(南京大学地球科学与工程学院/表生地球化学教育部重点实验室，江苏 南京 210023)

地下水反应运移模型具有参数个数众多，观测数据类型多样的特点。为了探究不同类型观测数据在反应运移模拟数据同化中的数据价值，构建了三氯乙烯降解反应运移模型的理想算例，基于水头和浓度两种类型观测数据，采用集合卡尔曼滤波方法推估渗透系数和贮水系数的非均质空间分布，讨论了影响同化结果的因素。结果表明：与仅同化水头数据的结果相比，联合同化水头和浓度观测数据推估渗透系数场和贮水系数场时具有更高的精度，在观测数据拟合和模型预测方面也有更好的表现。与目前溶质运移模型、非饱和流模型等地下水模型中的研究结果相似，数据同化结果受样本数量，观测井的数量和位置的影响，合理优化布置监测井和选择样本数量可有效改善数据同化效果并提高计算效率。

反应运移模型；参数估计；集合卡尔曼滤波；观测数据类型

地下水数值模拟具有易操作和广泛适用等特点，目前已逐渐成为地下水领域的主要研究方法之一[1]。其中，水文地质参数是数值模拟过程中必不可少的信息，但由于含水层的非均质[2]等复杂性质，许多水文地质参数的空间分布(如渗透系数等)在现有技术条件下无法快速准确获取，故利用一些易获取，精度良好的监测数据(如水头等)推估难以获取的水文地质参数分布成为了目前地下水领域的研究热点[3]。

非线性回归法和贝叶斯方法是目前地下水模型参数估计的两种主要方法，如Bachmaf等[4]利用非线性参数估计软件PEST[5]推估了水文地球化学反应的相关参数；Carniato等[6]利用贝叶斯方法对反应运移模型进行参数估计，并对残差相关性及模型误差进行了讨论。地下水反应运移模型综合了地下水水流模型，溶质运移模型以及水文地球化学模型，具有参数个数多，观测数据类型多样的特点，这给传统估计方法带来了极大的困难和挑战。鉴于传统方法在高维参数估计工作中存在计算效率和估计精度低下的缺陷以及参数多解的问题，数据同化方法被引入地下水模型的参数估计中。

数据同化方法包括变分方法、粒子方法、层次贝叶斯方法和卡尔曼滤波系列方法等[7]，其中集合卡尔曼滤波方法(Ensemble Kalman Filter，EnKF)[8～9]是卡尔曼滤波[10]的一种变体，其基于蒙特卡洛方法，通过统计样本调和模型预测与实际观测数据，进而给出当前状态和参数的最优估计。EnKF方法适用于处理大尺度非线性问题，最初用于海洋、气象学科，后逐渐扩展到水文地质领域[3,11～15]。沈晔等[14]系统地分析了集合卡尔曼滤波方法预测水头变化的原理及步骤，并展望了其在水文地质领域的应用前景；Chen等[15]针对承压水流运移问题，验证了EnKF方法联合更新参数和状态的效果，并讨论了集合大小、方差的选择等对同化结果的影响。

集合卡尔曼滤波方法在地下水溶质运移模型和非饱和流模型方面已有较多应用[3,13～15]，但目前鲜有应用于反应运移模型中。本文基于反应运移数值软件PHT3D[16]构建地下水反应运移理想算例，采用集合卡尔曼滤波方法(EnKF)联合水头和浓度两种类型观测数据以推估渗透系数和贮水系数的非均质分布，对比了在反应运移模型参数估计中单独使用水头数据和联合使用水头和浓度数据的同化效果。

1 方法

1.1地下水反应运移模型

常见的三维非稳定承压含水层地下水流运动方程为[17]：

式中：μs——承压含水层的贮水率；

H——承压含水层水头；

Kii——承压含水层xi方向渗透系数；

W——源汇项的单位体积流量；

t——时间。

给定边界条件和初始条件时，采用MODFLOW[18]数值方法求解该偏微分方程，计算得到各时间步长的地下水流场，代入对流—弥散方程[16]计算相应时间步长的地下水浓度场：

式中：Cn——第n种组分的总水相浓度；

Dii——流速方向与弥散张量主方向平行时的水动力弥散系数；

vi——沿xi方向的孔隙水实际平均流速；

rreac,n——由化学反应引起的浓度变化；

θ——孔隙度；

t——时间。

本文采用PHT3D软件求解该偏微分方程。

1.2集合卡尔曼滤波方法

定义x=[m,u]T为模型的状态向量，其中m是待估参数向量，维度为待估参数个数Nm。假设模型状态向量的集合样本数为Ne，第j个样本在第tk时刻的观测数据向量可表示为：

式中：dobs,j,k∈RNd；

Nd——观测数据个数；

dk——第tk时刻的实际观测值；

εj,k——观测误差。

对于第j个样本，在第k个同化步状态向量更新为：

式中：Cdobs,k——观测误差矩阵；

最后将Ne个样本更新后状态向量的均值作为第k个同化步各物理量的最优估计，即：

其中，〈·〉表示平均值。

2 理想算例

研究区为一个厚20 m，长宽均为21 m的平面二维承压含水层，假设含水层的孔隙度和弥散度在空间上均匀分布，取值如图1所示。图1所示的XY平面中上边界为定流量边界，Q=2.1 m3/d，其余含水层边界均为隔水边界，研究区初始水头为50 m。TCE在污染源区(6 m≤x≤10 m，16 m≤y≤20 m)的初始浓度为1.0 mg/L，其余区域初始浓度为0，其他各组分的初始浓度见表1。研究区内有2口定流量抽(注)水完整井和均匀布置的12口观测井，其中注水井流量Q1=10 m3/d，抽水井流量Q2=-12 m3/d，观测井每隔2 d观测一次，模型总模拟时间为20 d。本模型考虑TCE及其产物的降解反应，即：

图1 概念模型示意图Fig.1 Schematic diagram of the conceptual model注：ne—有效孔隙度；αL—纵向弥散度；αT—横向弥散度

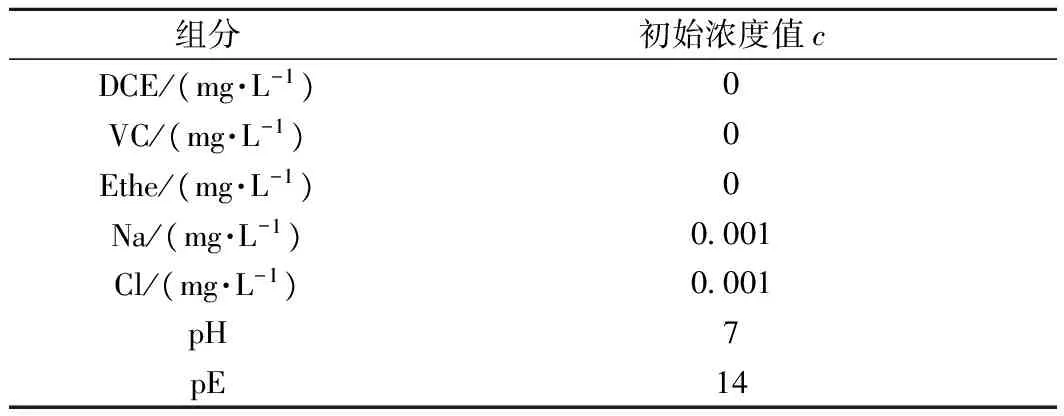
组分初始浓度值cDCE/(mg·L-1)0VC/(mg·L-1)0Ethe/(mg·L-1)0Na/(mg·L-1)0001Cl/(mg·L-1)0001pH7pE14

假设子母链式反应为一级动力学反应，则反应速率可以表示为：

式中：c——各组分的浓度；

k——一级动力学反应速率常数，各组分的一级动力学反应速率常数见表2。

假设渗透系数服从对数正态分布，贮水系数服从正态分布。对数渗透系数场Y1(Y1=ln(K))和贮水系数场Y2(Y2=μ*)的生成采用二维可分离指数型协方差函数：

CY(x1,x2)=CY(x1,y1;x2,y2)=

其中，Y1在x，y方向上的相关长度λx=10 m，λy=5 m，均值为-0.1，方差为1，Y2在x，y方向上的相关长度λx=20 m，λy=10 m，均值为1×10-4，方差为8.1×10-9。利用以上统计特征可采用KL分解[19](Karhunen-Loeve Decomposition)生成对数渗透系数场以及贮水系数场的参照场(图2)和样本场。

表2 TCE、DCE、VC的一级动力学反应速率常数取值表

3 参数估计

将参照场代入正模型，得到不同时刻水头和浓度的计算值，添加一定随机误差后得到用于参数估计的观测数据，考虑到水头和浓度测量的一般误差范围，假定水头和浓度的观测误差均服从正态分布，均值为0，前者标准差为0.01 m，后者标准差为真实值的10%。本文基于集合卡尔曼滤波方法将观测井处不同时刻的观测数据融入模型进行两组数据同化。其中算例1仅同化水头观测数据，算例2则联合同化水头和浓度两种类型的观测数据。均选取200个样本，同化10步，同化步长为2 d。

3.1参数估计结果对比评价

利用1～20 d水头和浓度的观测数据进行数据同化以推估对数渗透系数场和贮水系数场。由图2中均值图可见算例2的参数估计结果较算例1更接近于真实场，同时由标准差图可见算例2的样本标准差较算例1整体偏低，这说明联合同化水头和浓度观测数据时更新强度和更新范围都有所增加，进一步证明了浓度观测的数据价值，说明联合同化水头和浓度观测数据可有效提高同化效率，降低数据离散度，改善估计结果。

图2 均值和标准差综合对比图Fig.2 Comparison of the mean and standard deviation

3.2观测数据拟合和模型预测评价

为进一步说明联合同化水头和浓度观测数据以推估模型参数的优越性，将两个算例的参数估计结果带入模型进行数据拟合和模型预测评价。数据拟合效果越好，模型预测评价精度越高，说明模型参数估计效果越好。受篇幅限制，此处仅给出随机选取的三口观测井(4号、7号、12号)的观测数据拟合和模型预测评价结果。

图3和图4分别为算例1和算例2在4号、7号和12号观测井处同化时间段内(1 ～20 d)观测数据的拟合情况，对比可知在同化时间段内算例2终了时样本集合代入模型计算得到的水头和浓度数据与真实值更接近，尤其是浓度数据的拟合效果较算例1有明显提高。

图5为两个算例的终了样本集合在预测时间段内(20～40 d)观测井处水头和浓度数据的预测情况，可见联合同化水头和浓度观测数据时，模型的预测值与真实值更接近，尤其是浓度数据的预测效果明显改善。

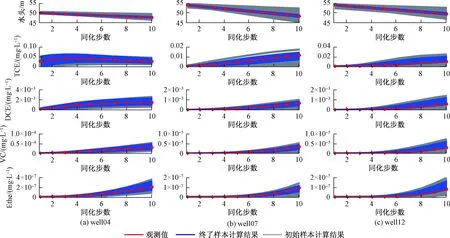
图3 仅同化水头数据时观测数据拟合情况Fig.3 Data match at several observation wells with only assimilating head data

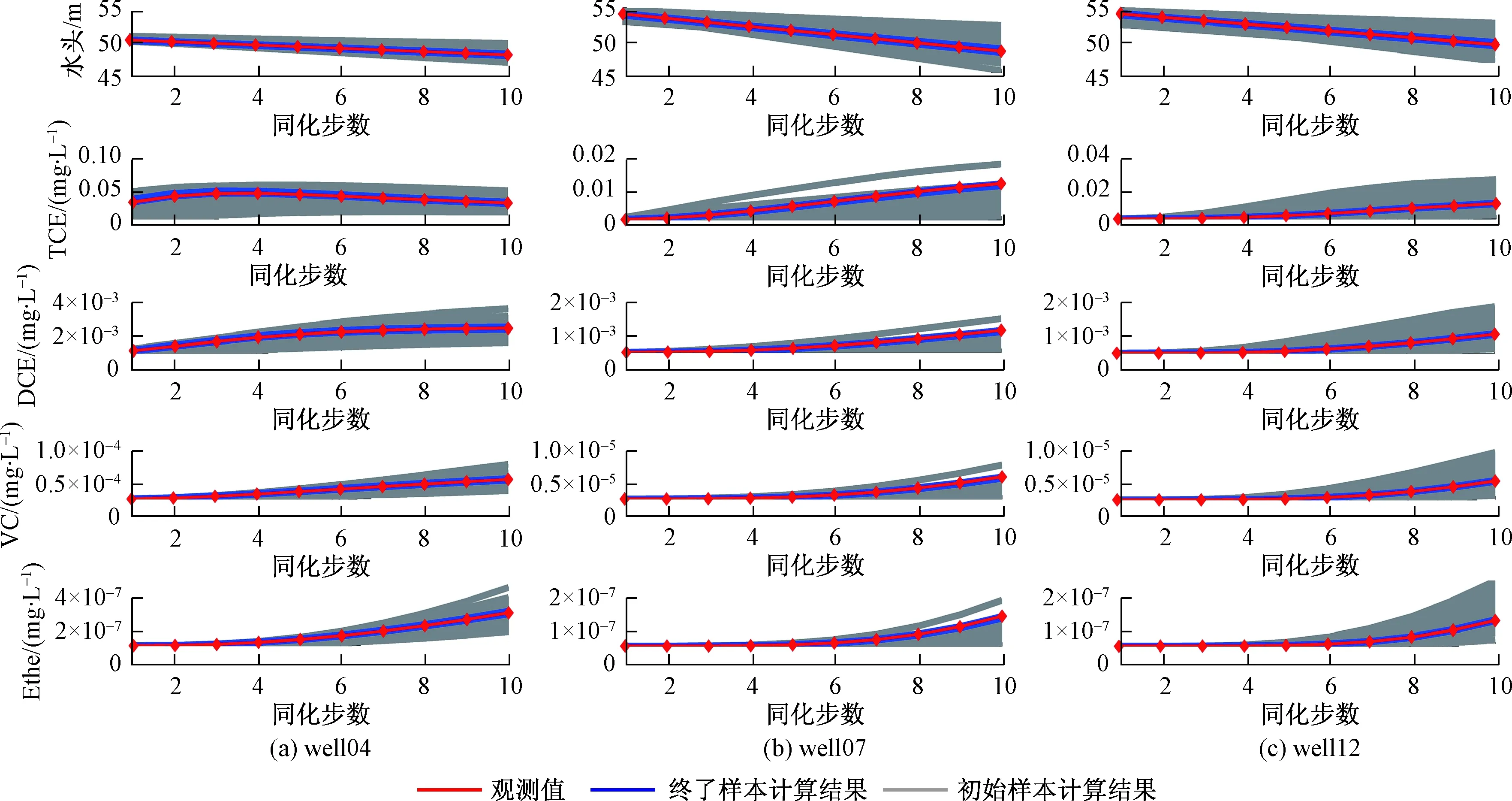
图4 联合同化水头和浓度数据时观测数据拟合情况Fig.4 Data match at several observation wells with jointly assimilating head and concentration data

图5 模型预测能力对比图Fig.5 Comparison of the predictability of the models

4 数据同化的影响因素分析

为了进一步探究地下水反应运移模型中不同因素对数据同化结果的影响，构建了多组数值算例，分别探究样本数量，观测井数量和位置对同化效果的影响。为简化模型，将贮水系数真实场作为模型已知条件，此处仅估计渗透系数场。并用均方根误差(RMSE)和集合离散度(Ensemble Spread,ES)简单评价数据同化效果：RMSE值越小说明参数估计结果与参照场越接近，ES值下降越快说明同化过程收敛越快。

Yi——每个格点的参照值；

var(xi)——每个格点处不同样本的方差。

4.1样本数量

由于EnKF是基于蒙特卡洛随机抽样的算法，理论上同化效果会随样本数量增加而改善，但计算时间也会随之增加，同时将会引入更多的误差，故样本数量与同化效果之间的关系值得探究。在其他条件一致时进行样本数量分别为50、100、200、300、400、500和1 000 时的数据同化，对其结果进行对比探究。

由图6可见样本数量过小(本模型中为50)时，RMSE值较大，同化效果差，甚至可能出现不收敛的情况；当样本数量达到一定值(本模型中为100)时，才能得到可接受的同化效果，此时该方法可用于模型的参数估计；随着样本数量的增加，同化过程的收敛速度逐渐降低，且同化效果可能会随样本数量增加而变差，如本模型中样本数量取1 000时，同化效果与样本数量为300时相当。由于随样本数量增加，更多的误差和不确定性被引入模型之中，从而导致同化效果变差。据图6可知，对于本模型，样本数量为100～500时同化效果较好。但随着样本数量增加，计算时间也随之增加，例如300个样本的计算时间比100个样本多7 h左右，但同化效果并未明显改善。综合考虑计算时间和估计精度，本模型中将样本数量设置为100较为合适。故研究者应从参数估计精度和计算时间两个方面综合考虑，确定合适的样本数量。

图6 不同样本数量的同化结果对比图Fig.6 Comparison of data assimilation results of different ensemble sizes

4.2观测井数量

实际工作中观测井的钻取及观测数据的获取均需要较高的成本，故了解观测井数量对于同化效果的影响对减少成本，提高工作效率具有重要的意义。在此选取空间布置相对均匀的5组观测井(图7)，观测井数量分别为2、4、6、8、12。数据同化的样本数量为100，同化步长为2 d，同化10步。

图7 不同数量观测井布局示意图Fig.7 Layout of different numbers of observation wells

由图8可见随着观测井数量增加，RMSE值逐渐减小，ES值下降速度逐渐增加，说明同化效果会随观测井数量增加而改善，收敛过程也随之加快。观测井从2口增加到4口时，RMSE明显下降，此后逐渐增加到6、8、12口观测井时，RMSE仍逐渐减小，但变化不再剧烈。故在实际工作中，可考虑建立地下水优化管理模型，综合考虑参数估计精度以及观测井的成本和经济效益，从而求出最优解，确定合适的观测井数。

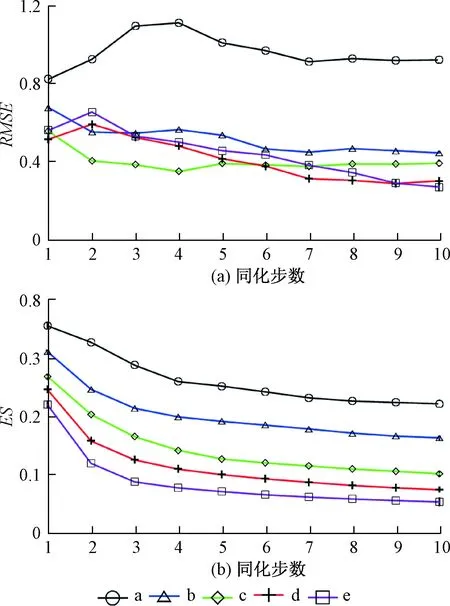
图8 不同数量观测井同化结果对比图Fig.8 Comparison of data assimilation results of different numbers of observation wells

4.3观测井位置

观测井数量一定时，探究观测井的位置是否会影响观测数据的数据价值，进而影响数据同化结果对于优化布置观测井，提高其利用效率有重要的参考价值。在其他条件一致时(样本数量为100，同化步长为2 d，同化10步)，考虑8口观测井下的三种随机布局(图9)。

图9 观测井布局示意图Fig.9 Schematic diagram of the layout of the observation wells

由图10可见数据同化的RMSE值以及ES值下降速度受到观测井位置的影响。由于观测井位置的改变，获取的观测数据价值和效用也随之变化，从而导致同化结果与收敛速度随之改变。但这里并未给出确定观测井最优布局的方法，故后续应进一步研究一定数量观测井下最优布局的确定方法，为实际工作中观测井的合理布置提供指导和帮助。

图10 三种布局情况下同化结果对比图Fig.10 Comparison of data assimilation results in the three layout cases

5 结论

(1)联合同化水头和浓度两种类型观测数据以推估渗透系数场和贮水系数场时估计精度更高，在观测数据拟合和模型预测方面也比仅同化水头观测数据更具优势。后续可考虑加入更多类型的数据进行同化，如地球物理数据、地下水温度数据等。

(2)样本数量，观测井的数量和布局都会对同化效果产生影响。总体看来，能够获取更多有效观测信息的观测井数量和位置，以及适当的样本数量可以使数据同化结果与实际更加接近，且计算时间适中，这与目前溶质运移模型、非饱和流模型等地下水模型中得到的结论基本一致。此外，如何选择合适的样本数量值得进一步探究；还可尝试建立综合考虑参数估计精度、观测井数量和布局的优化管理模型，从而通过数据价值方法获得最优参数估计方案。

[1] 薛禹群,谢春红.地下水数值模拟[M]. 北京:科学出版社,2007:1-5.[XUE Y Q，XIE C H. Groundwater numerical simulation[M]. Beijing: The Science Publishing Company,2007:1-5. (in Chinese)]

[2] 施小清，吴吉春，袁永生. 渗透系数空间变异性研究[J]. 水科学进展，2005，16(2)：210-215.[SHI X Q，WU J C，YUAN Y S. Study on the spatial variability of hydraulic conductivity[J]. Advances in Water Science，2005，16(2)：210-215. (in Chinese)]

[3] Zhou H，Gómez Hernández J J，Li L. Inverse methods in hydrogeology：evolution and recent trends[J]. Advances in Water Resources，2014，63(2)：22-37.

[4] Bachmaf S，Merkel B J. Estimating water chemistry parameters from experimental data using PEST with PHREEQC[J]. FOG-Freiberg Online Geoscience，2011，28：1-18.

[5] Doherty J，BrebberL Whyte P. PEST—Model-independent parameter estimation，user’s manual. 5th edition[M]. Brisbane Australia：Watermark Numerical Computing，2004：201-233.

[6] Carniato L，Schoups G，Van de Giesen N. Inference of reactive transport model parameters using a Bayesian multivariate approach[J]. Water Resources Research，2014，50(8)：6406-6427.

[7] 马建文,秦思娴. 数据同化算法研究现状综述[J]. 地球科学进展,2012,27(7):747-757.[MA J W，QIN S X. Recent advances and development of data assimilation algorithms[J]. Advances in Earth Sciences，2012，27(7)：747-757. (in Chinese)]

[8] Evensen G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics[J]. Journal of Geophysical Research，1994，99(C5)：10143-10192.

[9] Evensen G. Data assimilation the ensemble kalman filter[M].2nd ed. New York：Springer，2009:38-44.

[10] Kalman R. A new approach to linear filtering and prediction problems[J]. Journal of basic Engineering，1960,82(1)：35-45.

[11] Hamill T. Ensemble-based data assimilation：a review[J]. University of Colorado and NOAA-CIRES Climate，2002(1)：1-61.

[12] Keppenne C L，Rienecker M M. Initial testing of a massively parallel ensemble kalman filter with the poseidon isopycnal ocean general circulation model[J]. Monthly Weather Review，2002，130(12)：2951-2965.

[13] 史良胜,张秋汝,宋雪航,等.地下水位在非饱和水流数据同化中的应用[J]. 水科学进展，2015，26(3)：404-412.[SHI L S，ZHANG Q R，SONG X H，etal. Application of groundwater level data to data assimilation for unsaturated flow[J]. Advances in Water Science，2015，26(3)：404-412. (in Chinese)]

[14] 沈晔,李海涛,黎涛,等.地下水位预测：集合卡尔曼滤波(EnKF)应用概述[J].水文地质工程地质，2014，41(1)：21-24.[CHEN Y，LI H T，LI T,etal. Groundwater level forecast：overview of application of the Ensemble Kalman filter (EnKF)[J]. Hydrogeology & Engineering Geology，2014，41(1)：21-24.(in Chinese)]

[15] Chen Y，Zhang D. Data assimilation for transient flow in geologic formations via ensemble Kalmanfilter[J]. Advances in Water Resources，2006，29(8)：1107-1122.

[16] Prommer H，Post V. PHT3D，A reactive multicomponent transport model for saturated porous media. user’s manual V2. 10[J]. Groundwater，2010，48(5)：627-632.

[17] Bear J. Dynamics of fluids in porous media[M]. New York: American Elsevier Publishing Company,1972:764.

[18] Harbaugh A W，Banta E R，Hill M C，etal. MODFLOW-2000，the US geological survey modular ground-water model-User guide to modularization concepts and ground-water flow process[R]. US: Geological Survey open file report, 2000:7-19.

[19] Zhang D X, Lu Z. An efficient，high-order perturbation approach for flow in random porous media via Karhunen-Loeve and polynomial expansions[J]. Journal of Computational Physics, 2004,194(2):773-94.

责任编辑：张若琳

JointassimilationofheadsandconcentrationsforestimatingparametersofgroundwaterflowmodelsusingtheEnsembleKalmanFilter

LAN Tian, KANG Xueyuan, SHI Xiaoqing, WU Jichun

(KeyLaboratoryofSurficialGeochemistry,MinistryofEducation,SchoolofEarthSciencesandEngineering,NanjingUniversity,Nanjing,Jiangsu210023,China)

Reactive transport models are characterized by a large number of parameters and a variety of observations. Taking the TCE degradation model as an example, this article used the Ensemble Kalman Filter method to estimate the heterogeneous distribution of hydraulic conductivity field and storage coefficient field in order to compare the data values of different types of observations (i.e., only groundwater head, head and concentration) during the data assimilation. The results show that compared with only assimilating head data, jointly using head and concentration can improve the accuracy of parameter estimation and has a better performance in terms of data match and model prediction; the ensemble size and the number and location of observation wells will affect the results of the data assimilation, which is similar to the conclusions in other groundwater models such as the solute transport model and the unsaturated flow model. Better results and higher computational efficiency can be obtained by reasonably setting the layout of observation wells and choosing the ensemble size.

reactive transport model; parameter estimation; Ensemble Kalman Filter; observation data type

P641.2

A

1000-3665(2017)05-0006-08

施小清(1979-)，男，副教授，主要从事地下水数值模拟方面的研究。E-mail: shixq@nju.edu.cn

10.16030/j.cnki.issn.1000-3665.2017.05.02

2016-10-19;

2016-12-08

国家自然科学基金(41172206、41672229)；国家大学生创新训练计划(G201610284014)

兰天(1995-)，女，硕士研究生，主要从事地下水数值模拟工作。E-mail: lantnju@163.com