旋转型天线反射面型面误差高精度检测
季莉栓
(中国电子科技集团公司第五十四研究所,河北 石家庄050081)
旋转型天线反射面型面误差高精度检测
季莉栓
(中国电子科技集团公司第五十四研究所,河北 石家庄050081)
针对测量旋转型亚毫米波天线反射面型面误差精度低的问题,提出了基于三坐标测量机的测量方案。为消除接触测量时球形测头半径的影响,将设计的面天线向测头方向做法向等距面,形成半径补偿后的面天线。以轴向偏差为最小二乘拟合量,利用坐标变换将测量数据由测量坐标系转换到设计坐标系中,转换时考虑了天线反射面的边界约束问题。得到了旋转型天线反射面的型面误差。6次重复性测量得到的型面误差的变化量不超过4 μm。
三坐标测量机;旋转型天线反射面;型面误差;半径补偿;坐标变换
0 引言
反射面天线[1]的电气性能是通过机械结构实现的,而机械结构的调整依赖于高精度的几何量测量[2]。天线的型面误差可以评价天线的表面轮廓度,并可估计其引起的增益损失,型面误差越大则增益越低[3]。对面天线型面误差的检测,传统的测量方法有全站仪和经纬仪等,该方法的点位测量精度约为0.05 mm[4]。而面天线的工作频率越高,其型面误差的要求越小,对测量设备精度要求越高。对于亚毫米波天线[5],测量设备的精度应为μm级。因此,对于亚毫米波天线反射面型面误差的测量,传统的测量方法已无法满足使用要求。
在几何量测量领域,三坐标测量机因精度高、适用性强而有“测量中心”的美誉。高精度三坐标测量机的精度为0.001 mm左右[6],可用于亚毫米波天线反射面和天线模具等型面误差的测量。本文讨论了三坐标测量机测量旋转型天线反射面型面误差时测头半径补偿和坐标变换等关键问题,实现了天线反射面型面误差的高精度自动化测量。
1 旋转型天线反射面的数学模型
旋转型天线反射面有多种不同类型,不同类型反射面的方程是不同的,赋形反射面甚至只能给出数值解,为了能在软件中进行统一处理,需对反射面进行拟合,反射面方程的拟合精度可根据接收和发射信号的频率确定。设反射面的设计坐标系为:o-xyz,旋转型天线反射面的方程一般可以拟合为:
(1)
反射面的边界约束条件为:
(2)
式中,drange>0。
2 测头半径补偿
用三坐标测量机对反射面的型面误差进行测量时,需要球形测头与反射面接触点的坐标值,而采集的数据是球形测头球心的坐标值[7]。测头中心的拟合面与面天线z=f(x,y)是等距面[8]的关系,2个等距面的法向距离为测头半径r。为了消除测头半径r的影响,可将设计面天线z=f(x,y)向测头方向做法向等距面,形成半径补偿后的面天线z=g(x,y),如图1所示。
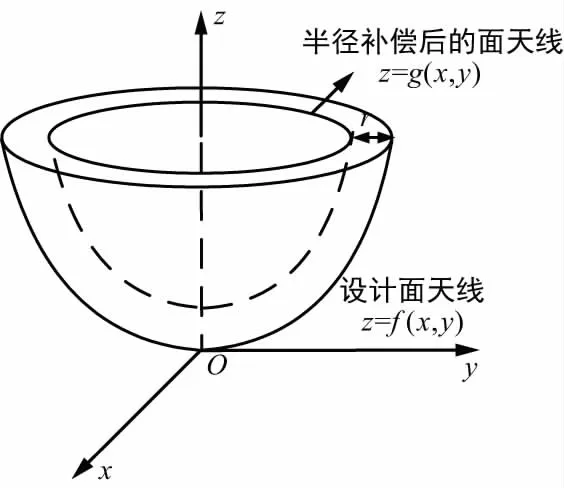
图1 设计面天线与半径补偿后的面天线
半径补偿后的面天线z=g(x,y)的边界约束条件可表示为:
(3)
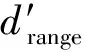
由于面天线z=f(x,y)是旋转面,半径补偿后的面天线z=g(x,y)也是旋转面,其形成过程是:先将设计面天线的一条母线沿测头方向做法向距离为r的等距线,然后再将该等距线[9]绕z轴旋转360°即可。
3 坐标变换
一般情况下,三坐标测量机的测量坐标系o′-x′y′z′与面天线的设计坐标系o-xyz并不一致,如图2所示。
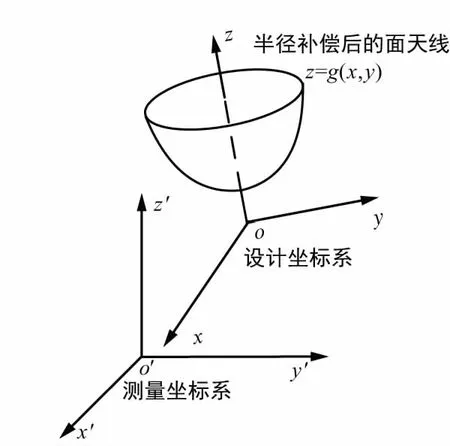
图2 测量坐标系与设计坐标系
反射面型面误差计算要解决2个坐标系的变换关系[10],坐标系的变换包括坐标系的平移和旋转。半径补偿后的面天线在设计坐标系o-xyz下的方程为:z=g(x,y),在测量坐标系下得到的M个测量点Pi′为(xi′,yi′,zi′),其中i=1,2,…,M。变换到设计坐标系下的点Pi为(xi,yi,zi),有
(4)
式中,(x0,y0,z0)为平移量;(α,β)为旋转角,均为求坐标变换时的未知量。
坐标变换时,一般是用测量数据和理论方程(无限大的理论曲面)进行最小二乘拟合,而实际的天线反射面只取理论曲面的一部分,这种拟合方法没有考虑实际的边界约束条件,可能出现天线偏离设计位置的情况。因此,在坐标变换时应考虑天线反射面的边界约束条件。在测量时,应尽量保证2个坐标系重合,一般2个坐标系的坐标轴会有2°(0.035 rad)以内的角度偏差,此时因α,β比较小时,边界约束条件可表示为:
(5)
式(5)把对(x0,y0,z0,α,β)的非线性边界约束条件转化成了线性约束条件,利用最优化方法可实现测量坐标系和设计坐标系的坐标变换。以轴向偏差为最小进行最小二乘拟合[11],即在边界约束条件下当所有测量点到面天线z=g(x,y)的轴向距离的平方和为最小[12]时,可以认为这时的(x0,y0,z0,α,β)是测量坐标系和设计坐标系的转换关系,即目标函数为:
(6)
求变换关系(x0,y0,z0,α,β)可以利用约束优化理论中的Rosen梯度投影法[13]。Rosen梯度投影法要求(x0,y0,z0,α,β)的初值要满足边界约束条件,而转换后的边界约束条件属于线性约束[14],可以通过求解线性不等式组[15]来得到(x0,y0,z0,α,β)的初值。利用初值通过迭代即可得到坐标变换的参数(x0,y0,z0,α,β)的值。
通过坐标变换将测量数据由测量坐标系转换到设计坐标系后,反射面的型面误差[16]定义为各测量点到理论反射面的法向偏差di的均方根[17],即型面误差ε为:
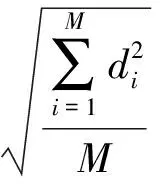
(7)
4 实测结果及分析
对某一个天线反射面的型面误差进行测量与计算,该反射面在设计坐标系下的边界约束条件为:-370 mm≤x,y≤370 mm。将该反射面固定在三坐标测量机的测量空间内,使面天线的设计坐标系尽量与三坐标测量机的测量坐标系重合,各坐标轴允许有2°以内的角度偏差。
将测量数据由测量坐标系转换到设计坐标系后,测量数据全部都在边界约束条件内,说明该算法中边界约束条件的有效性。各测量点的偏差如图3所示,从图3中可以看出,反射面的中间向下凹陷,四周向外凸起。
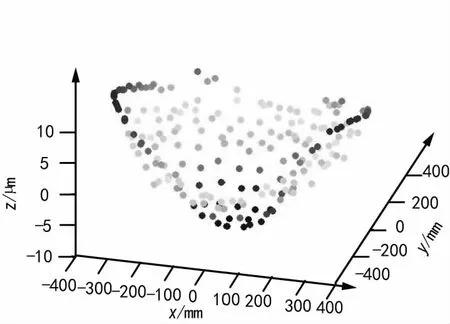
图3 反射面型面偏差的三维图
三坐标测量机的分辨率为0.1 μm,用该方法测得的最大法向偏差为8.3 μm和-9.7 μm,按式(7)计算的型面误差为4.7 μm(rms)。
按上述方法重复测量6次,得到的型面误差如表1所示,从表1中可以看出,该方法多次测量数据计算得到的型面误差值都比较接近,变化量在4 μm以内。可见基于三坐标测量机的测量方法能满足亚毫米波面天线对型面误差的要求。
表1 反射面的型面误差

测量次数123456型面误差/μm4.74.93.65.24.56.7
5 结束语
讨论了利用三坐标测量机对旋转型天线反射面的型面误差进行高精度检测,在数据处理过程中考虑了设计时的边界条件,使测量结果和设计更吻合。最终将反射面各测量点的偏差以三维图形直观地显示出来并得到型面误差。该测量方法适用于在室内环境下对中、小天线反射面的检测,具有精度高、重复性好、速度快且自动化等优点,特别适用于亚毫米波天线反射面、天线模具等对型面精度要求高的旋转型反射面的测量。该方法不仅能区分出加工合格的反射面,还能根据型面偏差指导反射面的加工,应用该测量方法能提高天线制造行业的工作效率。
[1] 杜彪,伍洋,张一凡,等.大口径反射面天线综述[J].无线电通信技术,2016,42(1):1-8.
[2] 李宗春,李广云.天线几何量测量理论及其应用[M].北京:测绘出版社,2009:2-3.
[3] 殷兴辉,徐之材,韩溥,等.大型天线表面精度实时检测[J].电波科学学报,2000,15(2):229-231.
[4] 李广云,李宗春.工业测量系统原理与应用[M].北京:测绘出版社,2011:2-3.
[5] 郑万章.中德亚毫米波望远镜的伺服系统设计[J].无线电通信技术,2014,40(4):56-59.
[6] 张国雄.三坐标测量机[M].天津:天津大学出版社,1999:1-2.
[7] 李春,刘书桂.三坐标测量机的测头半径补偿与曲面匹配[J].仪器仪表学报,2003,24(4):145-147.
[8] 单晨伟,廖恺,成宏军,等.一种叶片截面线光顺及等距面生成方法[J].航空制造技术,2015(1):115-118.
[9] 陈青,潘日晶,黄丽琴,等.基于渐进迭代逼近的等距曲线改进算法[J].福建师范大学学报,2015,31(5):12-19.
[10] 孙威,黄惠.机器人辅助的三维点云自动配准[J].集成技术,2015,4(6):37-45.
[11] 陈继华,李广云.离散点抛物面拟合的算法研究[J].天线技术,2005,35(4):32-34.
[12] 谢耿勋.基于遗传算法的形状误差算法的研究[D].沈阳:东北大学,2012:26-27.
[13] 龚纯,王正林.精通MATLAB最优化计算[M].北京:电子工业出版社,2014:175-178.
[14] 汤辰,徐亮,毕传兴.基于变换的线性约束斜投影波束形成算法[J].合肥工业大学学报,2014,37(1):14-18.
[15] 王晓民,乌力吉.求解线性不等式组问题的一种新算法[J].黑龙江大学自然科学学报,2007,24(3):349-352.
[16] 臧嗣鑫,李郝林.大型抛物面天线轮廓度评定方法[J].制造业自动化,2012,34(10):27-30.
[17] 王从思,段宝岩,仇原鹰.天线表面误差的精确计算方法及电性能分析[J].电波科学学报,2006,21(3):403-409.
TheHighPrecisionDetectionTechnologyofSurfaceErrorofRotatingAntennaReflector
JI Li-shuan
(The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)
A measurement method of the surface error of rotating sub-millimetre wave antenna reflector based on CMM is proposed to improve the measurement accuracy.The radius compensation reflector is formed as an offset surface towards the spherical head based on the designed reflector to eliminate the influence of the spherical head.The measurement data in the measuring coordinate system is transformed into the design coordinate system considering the boundary of the reflector in order to get the minimum of the axis deviation.The surface error is obtained at last.A reflector antenna is measured 6 times,and the variation of surface errors is no more than 4 μm.
CMM;rotating antenna reflector;surface error;radius compensation;coordinate transformation
10.3969/j.issn.1003-3106.2017.12.12
季莉栓.旋转型天线反射面型面误差高精度检测[J].无线电工程,2017,47(12):53-55.[JI Lishuan.The High Precision Detection Technology of Surface Error of Rotating Antenna Reflector[J].Radio Engineering,2017,47(12):53-55.]
TP391
A
1003-3106(2017)12-0053-03
2017-01-23
国际合作与交流基金资助项目(11261140641)。
季莉栓男,(1985—),工程师。主要研究方向:几何量计量、精密测量和机器视觉等。

