数字下变频中基于CORDIC算法的NCO设计
刘 刚,蒋伟进,董 胡,钟新跃
(1.长沙师范学院 信息与工程系,湖南 长沙410100;2.湖南商学院 计算机与信息工程学院,湖南 长沙 410205)
数字下变频中基于CORDIC算法的NCO设计
刘 刚1,蒋伟进2,董 胡1,钟新跃1
(1.长沙师范学院 信息与工程系,湖南 长沙410100;2.湖南商学院 计算机与信息工程学院,湖南 长沙 410205)
在数字下变频中传统数字控制振荡器(Numerically Controlled Oscillator,NCO)模块都是基于查找表结构的,该结构在FPGA内部实现需要占用大量ROM资源,针对这一问题,提出采用坐标旋转数字计算(Coordinate Rotation Digital Computer,CORDIC)算法进行NCO设计,相比传统的NCO设计,该方法具有输出信号频谱纯度高、能够直接混频而不需要乘法器等优点。设计中采用变象限映射方法解决CORDIC算法无法全周期覆盖的问题,采用流水线技术解决串行迭代带来难以实时输出的问题。经过Modelsim仿真分析,实际输出值与理论值之间的相对误差在10-4~10-5数量级范围内,满足数字下变频中NCO的性能需要。
数字下变频;坐标旋转数字计算方法;流水线;数字控制振荡器;现场可编程门阵列
0 引言
在软件无线电接收机中,数字下变频器是把ADC数字化后的高速数字中频信号变为低速的基带信号,便于后续的相关处理。数字下变频器在这里起到前端ADC和后端通用DSP器件之间的桥梁作用,其性能的优劣会对整个软件无线电系统的性能产生直接的影响[1]。因此,数字下变频技术成为软件无线电接收机的关键技术之一,成为制约软件无线电性能的重要器件之一[1]。文献[2-3]中采用基于多相滤波结构来设计实现数字下变频器,虽然在一定程度上能够节省FPGA内部资源和实现高速数据流下数字下变频,但在性能上还有较大的提升空间,因为只有改进和优化数字下变频中NCO这一核心模块才能大幅度提高数字下变频的性能。传统的数字下变频的NCO是基于查找表的形式实现的[4],这种方法虽然在FPGA内部实现起来方便简单,但同时也存在占用大量ROM资源,需要复杂的乘法计算,以及输出信号频谱杂散较大而导致的精度不高等缺点。而基于CORDIC算法实现的NCO就能很好地克服上述缺点[5-6],因此本文重点研究应用于数字下变频的CORDIC算法的设计与实现。
综上,现阶段我国体育旅游产业市场有着巨大潜力,对体育旅游专业方向的复合应用型人才有相当大的需求。为满足庞大的市场人才需求,体育旅游专业人才的培养成为我国体育旅游产业可持续发展不容忽视的课题。
1 数字下变频结构和原理
1.1 数字下变频结构
开沟诱笋。第1次翻耕后,沿林地水平带开沟,沟宽50 cm、深30 cm,于沟中填埋林下剩余物粉碎料,然后覆土。目的是利用有机质废料的保湿、透气等特点,诱导竹鞭,促其笋芽萌发生长。两沟间隔以120~150 cm为宜。
数字下变频采用的结构如图1所示,该结构由混频模块和抽取滤波模块组成。混频模块实现的功能是把数控振荡器NCO产生的正余弦本振信号分别与采样信号相乘实现混频,产生I和Q两路信号[7]。抽取滤波模块实现的功能是首先把混频后的信号进行抽取降速处理,然后通过低通滤波器滤除无用的谐波分量,得到I和Q两路数字基带信号[8]。数字下变频就是基于这种方式来完成对数字信号的降频处理。

图1 数字下变频结构
从式(6)可以看出,每一次旋转实现只需进行简单的移位和相加操作,易于在FPGA内部实现。为了便于追踪累加旋转角度,引入角度累加器方程:
CORDIC算法原理如图2所示。
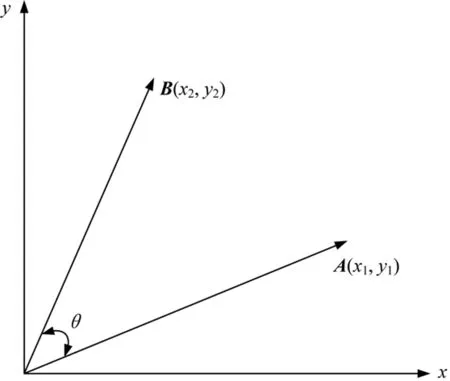
图2 CORDIC算法原理
设有一个向量A(x0,y0)经逆时针旋转角度θ得到向量B(x1,y1),根据极坐标变换规则可得[9]:
(1)
旋转角度θ也可以通过经过多次旋转小角度θn而得,则单次旋转变化表达式为:
在这股全民P图的浪潮中,可以看到,个体在参与该事件的过程中,完全是以一种消遣性的态度来主导政治事件的走向。而个体对政治事件的消遣性行为,消费了该事件的政治性,使得事件走向了娱乐化。无独有偶,会理县人民政府居然利用“悬浮照”事件,顺势推广了县里的旅游业,反过来消费了网民。在消费主义思潮影响下,个体和组织以消遣性态度参与政治活动,将政治事件推向了娱乐化的轨道。
(2)
由于CORDIC算法是进行多次迭代运算来完成相幅转换的,且下一次迭代旋转方向需根据上一次迭代后的剩余旋转角度值来进行判断,所以在数字下变频中高精度NCO要求下的CORDIC算法的多次迭代会导致难以实时输出[15]。为此本设计根据数字下变频的需要采用流水线技术来解决上述问题。它使得每个迭代运算单元在一个时钟周期内并行工作,虽然经过n个时钟周期才有第一个计算值输出[16],但后面所有的计算值都只需要一个时钟周期输出,相比没有采用流水线技术的CORDIC算法在计算速度上提高了n倍[17]。
(3)
为了便于硬件实现,令θn=arctan(2-n),则式(3)可变为:
(4)
由于经过N次小角度旋转,角度θ与单次旋转角度θ执行结果一样,所以利用式(4),式(1)也可等价为:
(5)

(6)
1.2 CORDIC算法的基本原理
zn+1=zn-δnθn。
(7)
当初值(x0,y0,z0)分别对应于(K,0,θ)时,经过n次迭代旋转后,角度累加器zn+1趋于0时,对应的xn,yn就分别为cosθ和sinθ。CORDIC算法就是通过这种方式来完成正余弦计算的。
1.3 NCO基本原理
基于CORDIC算法的NCO结构如图3所示,其主要思想是通过不断周期性地相幅转换来实现正余弦信号的,输入的频率控制字和相位控制字分别控制相位增量和初始相位,从而起到控制输出信号的频率和初相位的作用[11]。
赋矿层礁灰岩礁灰岩存在许多孔隙,如沉积物原生孔洞(隙)、砂(砾)之间空隙、岩石(层)之间差异收缩裂(空)隙、层间裂隙等,这些孔洞(隙)成为储矿空间含矿。
1.2.1 一般治疗 予严格单间隔离、心电监护、持续鼻导管吸氧、物理降温及营养支持,乌司他丁减轻炎症反应,丙种球蛋白增加抵抗力,喜炎平注射液及连花清瘟胶囊清热解毒;并加用莫西沙星抗细菌治疗,疗程6 d;因1,3-β-D葡聚糖检测试验(G试验)阳性,加用伏立康唑抗真菌治疗,疗程9 d。

图3 基于CORDIC算法的NCO结构
基于CORDIC算法的NCO与传统的NCO在结构上类似,主要区别是前者通过移位相加的方式进行相幅转化计算,而后者是把相位累加器输出的实时相位作为查找表的地址,而查找表中对应地址的内存单元储存值就是该相位对应的正余弦幅度值,是通过不断向查找表取值输出来完成相幅转换的。采用CORDIC算法来完成数字下变频中的NCO模块相比于基于查找表的NCO,除了前面提及的优点外,它还能在CORDIC模块内与接收的输入信号x(n)直接相乘,这样使得其在完成NCO的同时完成了混频的功能[13]。
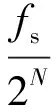
(8)
式中,f0为系统输出频率;FW为频率控制字的值;N为频率控制字的二进制位宽;fs为系统的工作频率。
NCO输出的频率与频率控制字之间的关系为[12]:
回到家里,一股无名火就上来了,其实也就是一种怨气。下面是空的,难道上面还不许往里塞东西吗?她就大嚼了一顿黄瓜,还啃了一堆野桃子,脖子一伸一缩的,被撑得不能动弹了。红琴仰面躺在木床上,屋子里异常地静谧,一只乌鸦在门口的树枝上栖息着,聒噪了两声,忽然展翅飞走了。它飞了一阵子,又落到了远处的田塍上。空旷的田野上,稻子刚刚收割掉,偶尔也有几只青蛙不甘寂寞地叫两声,打破这乡野独有的恬静。
2 基于CORDIC算法的NCO设计
表1 CORDIC算法输出端的象限映射表
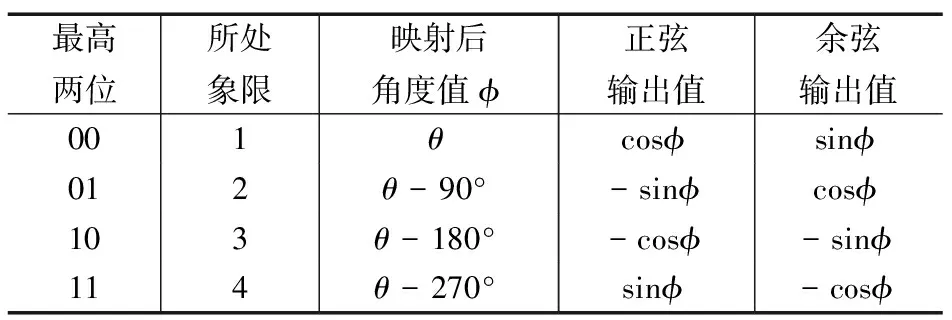
最高两位所处象限映射后角度值ϕ正弦输出值余弦输出值001θcosϕsinϕ012θ-90°-sinϕcosϕ103θ-180°-cosϕ-sinϕ114θ-270°sinϕ-cosϕ
式中,δn为单次旋转方向,当逆时针旋转时,δn=1;当顺时针旋转时,δn=0。提取cosθn,式(2)也可写为[10]:
3 仿真与结果分析
设计采用Altera的CycloneII系列EP2C8Q208C8芯片完成设计,通过编译后进行仿真测试,仿真结果如图4所示。

图4 Modelsim仿真结果
从图4可以看出,本设计能够实时输出2路正余弦信号,且可通过改变频率控制字来控制输出信号的频率。该仿真前面4个频率控制字分别为h0080、h0100、h0180和h0200,当系统工作时钟为100 MHz时,其输出信号频率分别对应为195.312 5 kHz、390.625 kHz、585.937 5 kHz和781.25 kHz。相幅转换的实际值和理论值的对应关系如表2所示[7]。
表2 输出的实际值和理论值的比较
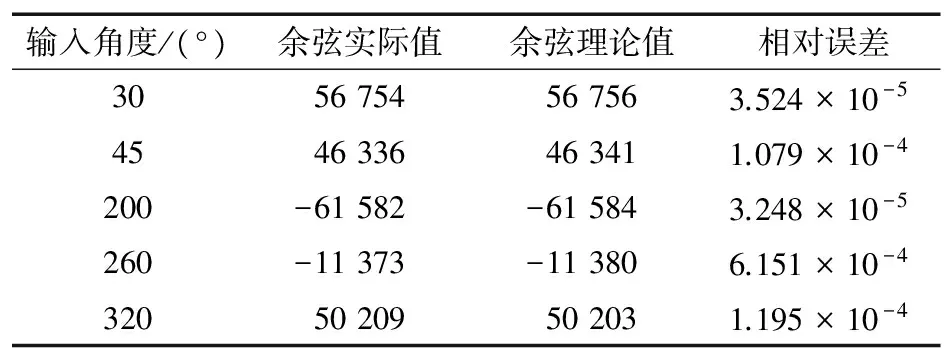
输入角度/(°)余弦实际值余弦理论值相对误差3056754567563.524×10-54546336463411.079×10-4200-61582-615843.248×10-5260-11373-113806.151×10-432050209502031.195×10-4
从表2中比较分析看出,输出结果与理论值之间相对误差在10-4~10-5数量级范围内,基本上满足数字下变频模块中的NCO的需要。
4 结束语
本文采用基于CORDIC算法在FPGA内部设计实现数字下变频中的NCO模块,通过对CORDIC算法理论分析,采用变象限和流水线方法对其进行优化改进,并运用Verilog语言在FPGA内部实现。通过对该设计进行Modelsim仿真分析,其结果满足设计需要,解决了传统基于查找表结构的NCO在FPGA内部占用大量的ROM资源的问题,并具有较高的精度和速度。
“啊,嘴巴再张大一点……”医生检查完妍妍的扁桃体,又拿起听诊器,仔细地听了又听。妍妍一声不响,乖巧地听医生指挥。收起听诊器,医生一边拿起笔飞快地在病历卡上写诊断书,一边慢悠悠地抬起头,对妍妍说:“小朋友,以后要多吃米饭,多吃水果和蔬菜,这样你才会长得更高!”顿了顿,然后又说,“不用开药。”妍妍睁大了眼睛,不可思议地看着医生。
[1] 李汉波.基于FPGA平台数字信道化接收机的开发与研制[D].西安:西安电子科技大学,2009.
[2] 陶杰,李骏,张水兴,等.DMR系统中数字下变频技术分析[J].无线电工程,2014,44(8):34-37.
[3] 刘二平,刘晓杰.基于多相滤波的高效数字下变频设计[J].无线电工程,2016,46(8):23-26.
[4] 杨豪,颜青,马舜尧.基于进位链优化方法的高速NCO设计[J].无线电工程,2014,44(1):72-74,80.
[5] 王顶,刘太君,叶焱.基于改进CORDIC算法的数字预失真实现[J].无线电通信技术,2014,40(3):68-71.
[6] 顾明超,李倩.宽带数字下变频器的FPGA实现[J].无线电通信技术,2014,40(5):69-72.
[7] 郭勇,梅大成,邢丹.基于CORDIC算法数字下变频器设计[J].计算机与信息技术,2007(11):15-18.
[8] 许彦辉,年夫顺,许建华,等.基于CORDIC算法实现数字下变频[J].信息系统工程,2011(4):15-18.
[9] 祁艳杰,刘章发.基于Parallel_CORDIC的高精度高速度直接数字频率合成器的FPGA实现[J].电子学报,2014,42(7):1392-1397.
[10] 张朝柱,韩吉南,燕慧智.高速高精度固定角度旋转CORDIC算法的设计与实现[J].电子学报,2016,44(2):485-490.
[11] 侯武威,袁安民,赵颖辉.基于CORDIC算法的数字下变频技术设计与实现[J].电子设计工程,2012,20(9):35-37.
[12] 闫温合,胡永辉,李瑾琳,等.应用于数字下变频中CORDIC算法的FPGA实现[J].时间频率学报,2014,37(1):34-40.
[13] 郭连平,田书林,王志刚,等.并行数字下变频中的NCO实现研究[J].仪器仪表学报,2012,33(5):998-1004.
[14] 任小西,沈建龙.低时延-消耗的CORDIC算法及结构的研究[J].计算机科学,2014,41(8):25-29.
[15] 吉炜寰,邹玉炜,黄磊.基于全流程并行加速的改进数字下变频器设计[J].电子器件,2017,40(1):142-146.
[16] 谢建华,阮圆,孙锋.基于CORDIC算法的流水线型DDS设计[J].微计算机信息,2008,(29):286-287.
[17] 王佳琪,熊先越.基于FPGA的流水线CORDIC算法的DDFS设计[J].光通信技术,2012,36(4):61-62.
DesignofNCOBasedonCORDICAlgorithminDigitalDown-conversion
LIU Gang1,JIANG Wei-jin2,DONG Hu1,ZHONG Xin-yue1
(1.DepartmentofInformationandEngineering,ChangshaNormalUniversity,ChangshaHu’nan410100,China; 2.CollegeofComputerandInformationEngineering,HUNANUniversityofCommerce,ChangshaHu’nan410205,China)
In digital down conversion,the traditional NCO module is based on look-up table structure,which takes up a large amount of ROM resources in FPGA.In order to solve this problem,this paper uses the Coordinate Rotation Digital Computer (CORDIC) algorithm for NCO design.Compared to the traditional NCO design,this method has high spectral purity,can be directly mixing without multiplier.In the design,a variable quadrant mapping method is adopted to solve the problem that CORDIC algorithm can not be covered by full cycle.The pipeline technology is used to solve the problem that the serial iteration is difficult to output in real time.The results of Modelsim simulation analysis show that the relative error between the actual output value and the theoretical value is 10-4-10-5,which satisfies the performance requirement of NCO in digital down-conversion.
digital down-conversion;CORDIC algorithm;pipeline;NCO;FPGA
10.3969/j.issn.1003-3106.2017.12.16
刘刚,蒋伟进,董胡,等.弹性拓扑控制技术研究[J].无线电工程,2017,47(12):71-74.[LIU Gang,JIANG Weijin,DONG Hu,et al.Design of NCO Based on CORDIC Algorithm in Digital Down-conversion[J].Radio Engineering,2017,47(12):71-74.]
TN911
A
1003-3106(2017)12-0071-04
2017-03-27
国家部委基金资助项目。
刘刚男,(1981—),硕士,讲师。主要研究方向:基于FPGA的软件无线电和5G通信。
蒋伟进男,(1965—),硕士,教授。主要研究方向:计算社会学、管理系统模拟、复杂系统建模和仿真、信息系统安全、云计算与大数据技术研究。

