基于高程信息的卫星访问计算方法
赵汝哲,林 元,彭会湘,员建厦,张万玉
(1.中国电子科技集团公司第五十四研究所,河北 石家庄050081;2.北京市遥感信息研究所,北京 100192;3.陆军北京军代局驻石家庄地区军代室,河北 石家庄050081)
基于高程信息的卫星访问计算方法
赵汝哲1,林 元2,彭会湘1,员建厦1,张万玉3
(1.中国电子科技集团公司第五十四研究所,河北 石家庄050081;2.北京市遥感信息研究所,北京 100192;3.陆军北京军代局驻石家庄地区军代室,河北 石家庄050081)
成像卫星任务规划的基础是访问分析,而其核心是计算卫星对目标的访问信息,即卫星对目标的观测时间和观测姿态角度。现有卫星任务管控系统中使用的卫星访问信息计算方法通常没有考虑目标高程信息,这使得对高海拔地区目标的观测姿态角度计算不够准确。提出一种基于目标高程信息改进的卫星访问信息计算方法,在构建卫星与目标的空间计算模型时,考虑目标的高程信息,计算得出更为准确的观测姿态角度,使得按此角度做规划后的卫星能够精确地拍摄到目标位置。实验结果表明,该算法降低了系统误差,提高了卫星观测精度。
成像卫星;对地观测;访问计算;高程信息
0 引言
目前成像卫星任务规划系统主要分为3个阶段:访问分析、任务分解和任务规划[1-2]。其中访问分析是任务分解和任务规划的前提,主要是依据卫星运行轨迹和地面上各个目标位置,计算出卫星对所有目标的访问时间窗口[3-5],然后针对每一个目标计算出卫星在各个访问时刻对该目标的观测姿态角度信息。以此计算结果为依据选择卫星资源,根据卫星对目标的访问时间窗口对观测任务进行分解,然后得到一系列观测元任务[6-8]。这些元任务都是由某颗卫星在指定时间以指定姿态角度一次性观测成像完成,是不可分割的原子任务[9-12]。以这些观测元任务作为任务规划算法的输入,可以有效提升求解空间的搜索性能[13-14],并且可以精确控制卫星对地面目标的观测成像。因此,访问分析是卫星任务规划的基础[15-17]。
现有卫星任务管控系统采用的访问信息计算方法通常都没有考虑目标的高程信息对卫星观测姿态角度计算的影响[18-21]。以这样的计算结果做规划控制卫星成像,对于海平面上高程信息为0的目标观测没有影响,对于高程绝对值较小的平原低海拔目标的观测会有较小偏差,对于高程绝对值比较大的高海拔地区目标或山谷底部目标的观测会有较大偏差,这就导致某些幅宽较小的卫星在该时刻以指定角度拍摄成像,根本就拍摄不到目标位置。因此,在计算卫星对目标的观测姿态角度时,要考虑目标高程信息对计算结果的影响。
针对上述问题,本文提出了基于目标高程信息改进的访问计算方法,设计卫星与目标的空间计算模型时,增加考虑目标高程值因素,最后通过实际卫星观测地面目标样例验证了算法合理性。
1 卫星与目标的空间计算模型
首先构建卫星与目标的空间计算模型,星载传感器中心光轴初始指向地心,然后卫星按照某个角度姿态机动后,星载传感器中心光轴即可指向目标位置进行观测。在此过程中忽略卫星质心与星载传感器之间的距离。由此可知,计算卫星访问信息实际上是计算卫星以何种角度进行姿态机动后,传感器中心光轴就能准确指向目标位置。计算该姿态机动角的流程如图 1所示。
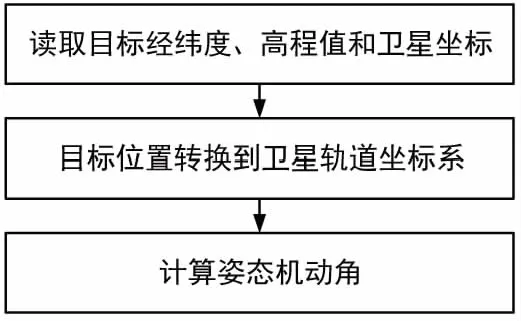
图1 卫星访问姿态机动角计算流程
1.1 目标点地理坐标和高程值到地心空间直角坐标系(地固系)坐标的转换
如果目标T地理坐标(测地经纬度、高程值)为(lon,lat,h),那么经过坐标转换之后,T在地心空间直角坐标系中坐标为:
(1)
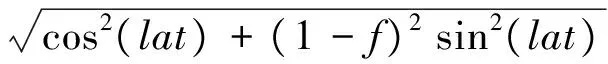
1.2 目标点地固系坐标到瞬时真赤道地心系坐标的转换
将目标T在地固系中的直角坐标近似为准地固系中的直角坐标,此时将准地固系中的直角坐标转换到瞬时真赤道地心系的公式为:
V1(T)=Rz(-SG(t))V0(T),
(2)
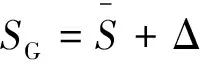
1.3 目标点由瞬时真赤道地心系坐标到瞬时平赤道地心系坐标的转换
这里需要考虑章动的影响,将目标点由瞬时真赤道地心系转换到瞬时平赤道地心系坐标之后为:
V2(T)=Rz(Δμ)Ry(-Δθ)Rx(Δε)V1(T),
(3)
式中,Δμ=Δφcosε为赤经章动;Δθ=Δφsinε为赤纬章动;Δε为交角章动;Δφ为黄经章动。
1.4 目标点瞬时平赤道地心系坐标到历元平赤道地心系坐标的转换
目标点经过转换之后的历元平赤道地心系(J2000 惯性系)中的坐标为:
V3(T)=Rz(ζA)Ry(-θA)Rz(zA)V2(T),
(4)
式中,ζA、θA和zA为3 个赤道岁差参数。
1.5 目标点历元平赤道地心系坐标到地心轨道坐标系坐标的转换
转换后的目标点在地心轨道坐标系中的坐标为:
V4(T)=Rz(ω+f)Rx(i)Rz(Ω)V3(T),
(5)
式中,Ω为历元时刻t对应的卫星升交点赤经;i为历元时刻t对应的卫星轨道倾角;ω为历元时刻t对应的卫星近地点幅角;f为历元时刻t对应的卫星真近点角。
1.6 目标点地心轨道坐标系坐标到卫星轨道坐标系坐标的转换
目标点坐标由地心轨道坐标系经坐标系旋转,然后再沿Z轴平移转换到卫星轨道坐标系后为:
(6)
式中,RES为历元时刻t对应的卫星质心到地心的距离。
1.7 卫星访问姿态角度计算
经过上述几步坐标转换,可以计算出任意时刻t某个地面目标T在卫星轨道坐标系下的空间坐标,即把目标坐标与卫星坐标统一到同一坐标系中。在卫星本体坐标系中,卫星相机光轴指向卫星本体坐标系Z轴,在卫星没有进行姿态机动时,卫星本体坐标系与卫星轨道坐标系重合,坐标系Z轴都指向地心。因此,卫星要想准确观测该目标,就需要把相机光轴通过姿态机动后指向目标T,卫星访问姿态角即为卫星本体坐标系Z轴相对于卫星轨道坐标系Z轴的转动角度,示意图如图 2所示。
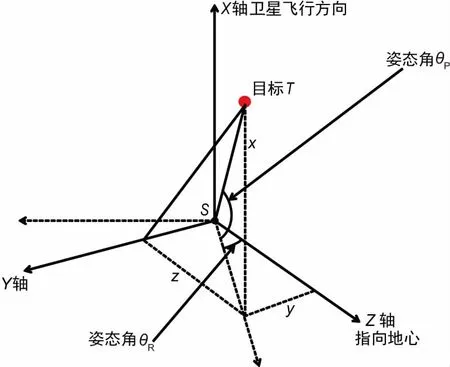
图2 卫星与地面目标在卫星轨道坐标系下的示意图
卫星相机光轴指向矢量在卫星本体坐标系中为(0,0,1),即指向卫星本体坐标系Z轴;若要观测到目标,卫星星体先绕X轴姿态机动角度θR,再绕Y轴姿态机动角度θP后,相机光轴(本体坐标系Z轴方向)指向目标位置。由图 2可知,姿态角θP、姿态角θR为:
(7)
根据t时刻目标转换到卫星轨道坐标系下的坐标(xt,yt,zt),由式(7)就可以确定θP和θR。
对于成像卫星,当卫星飞行至目标所在横截面时,卫星距离目标位置最近,此时最适合观测成像,如图 3所示,X轴(卫星飞行方向)垂直纸面向里。
此时x=0,由式(7)可知姿态角θP为0,可计算得出此时卫星访问目标的姿态角θR。如图 3所示,对海拔高度为h的目标T1做访问计算时,如果不考虑高程值h,则变成对地面投影伪目标T0做访问计算,会引入姿态角系统误差。
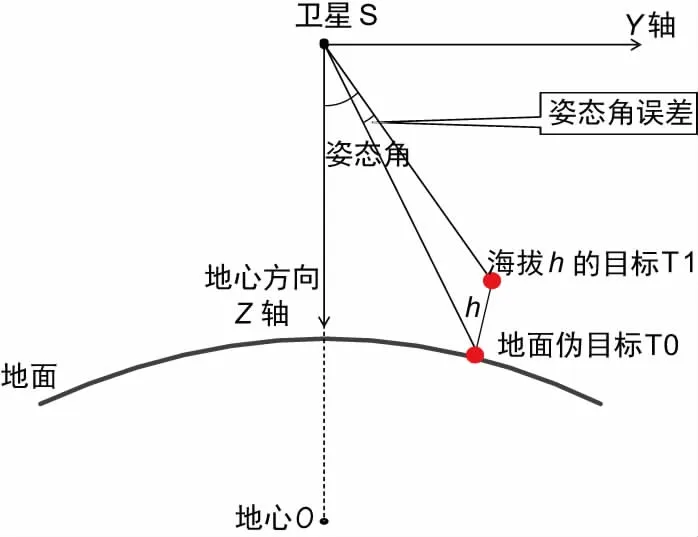
图3 卫星最佳访问时刻姿态机动示意
2 误差影响分析
目标高程信息引入的系统误差分别对SAR成像卫星和可见光成像卫星任务规划产生影响。
SAR成像卫星:由于SAR成像卫星的成像模式是根据姿态角所在的波束范围去选择合适的波位进行成像,如果姿态角计算有偏差,则会导致选择波位错误,所以对目标访问信息的计算精度要求非常高。如果不考虑高程信息进行访问计算,那么对高海拔地区目标的访问计算实际上是按照高程值为0的伪目标点(即水平面上的投影位置)进行计算,这样得到的卫星姿态角其实是星上相机针对伪目标点的姿态角,与真实目标点的实际姿态角必然有偏差,而且该偏差会随着高程绝对值增大而增大,姿态角偏差增大到一定程度,就会导致后续做任务规划选择成像波束错误,卫星载荷执行结果必然是无法观测到真实目标点位置。
可见光成像卫星:可见光成像卫星的成像模式是用星上CCD相机按照任务规划指定角度拍摄成像,光轴中心指向目标点位置。如果姿态角计算有偏差,则会导致按照该角度进行拍摄后,目标点位置与图像中心点有偏差。如果不考虑真实目标点高程信息,即按照高程值为0的伪目标点(水平面上的投影位置)进行访问计算,这样计算得到的姿态角与真实目标点的实际姿态角有一定偏差,该偏差随高程绝对值增大而增大。按此姿态角进行任务规划观测成像后,图像中心点与真实目标点位置必然有一定距离偏差。如果姿态角偏差增大到一定程度,图像中心点与真实目标点的距离偏差超过卫星相机1/2幅宽时,那么在卫星拍摄的图像中将无法观测到真实目标点位置。
3 实验结果分析
根据上述算法原理及误差影响分析,选择某卫星做实验,代入具体卫星参数,得到该卫星在最佳访问时刻访问某个目标时的姿态角。
该星访问目标点位置时,计算得出姿态角随目标高程值变化的情况如表1所示。观测偏差距离为按照考虑高程值的姿态角规划卫星观测的成像中心点与高程值为0的姿态角规划的成像中心点的地面距离,该星轨道高度为540 km。姿态角误差随高程值变化趋势如图4所示,观测偏差距离随高程值变化趋势如图5所示。
表1 某卫星观测目标信息随高程变化情况
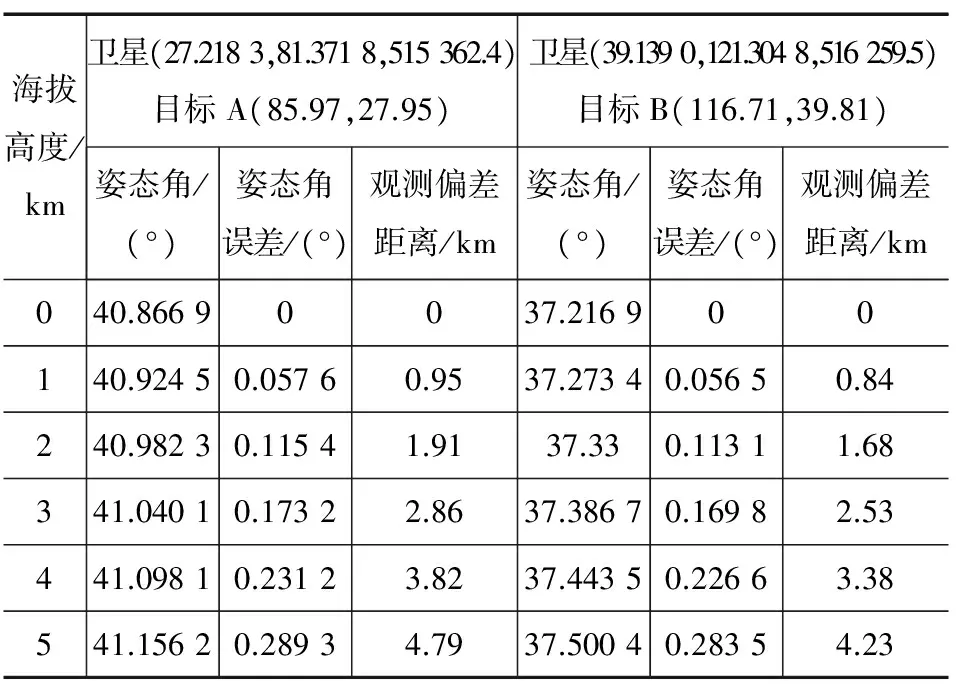
海拔高度/km卫星(27.2183,81.3718,515362.4)目标A(85.97,27.95)卫星(39.1390,121.3048,516259.5)目标B(116.71,39.81)姿态角/(°)姿态角误差/(°)观测偏差距离/km姿态角/(°)姿态角误差/(°)观测偏差距离/km040.86690037.216900140.92450.05760.9537.27340.05650.84240.98230.11541.9137.330.11311.68341.04010.17322.8637.38670.16982.53441.09810.23123.8237.44350.22663.38541.15620.28934.7937.50040.28354.23
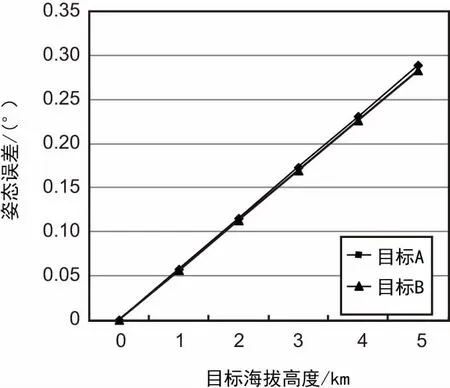
图4 姿态角误差随高程值变化示意
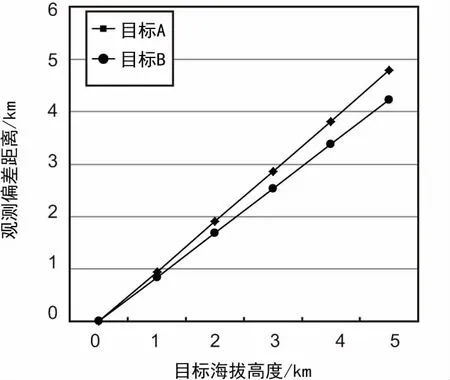
图5 观测偏差距离随高程值变化示意
目前可见光成像卫星幅宽一般为15~70 km,某些高分辨率的可见光卫星幅宽是8 km,某些高分辨率SAR卫星最小波束范围是0.1°,姿态角误差超过该值,SAR载荷就会选择下一个波位进行成像。由实验结果可以看出,无论是针对哪个经纬度位置的目标,当不考虑目标高程信息时,随着目标点实际高程值增大,根据高程值0计算得到姿态角的系统误差会逐渐增大,按此姿态角进行观测成像的偏差距离会越来越大,一旦该偏差距离超过星上相机1/2幅宽,或者姿态角误差超过SAR载荷波束范围,则导致卫星按此规划执行后无法观测到真实目标点。由此可以得出,成像卫星任务控制系统中,在对海拔较高的目标计算卫星访问信息时,必须考虑目标所在位置的高程值,不然做卫星任务规划方案时,会产生不可接受的系统误差,这种误差增大到一定程度,将导致卫星实际上根本观测不到目标位置。
4 结束语
针对卫星访问计算问题,增加考虑高程值因素,提出基于高程信息的卫星访问计算方法。该方法可以消除不加高程信息算法的系统误差,提高了卫星访问目标的姿态角计算精度,使得卫星能更准确地观测目标。尤其是高分辨率成像卫星对高海拔地区目标做任务规划时,必须得先用该方法进行访问计算,然后按此计算结果进行规划,才能指导卫星准确观测到目标位置。
[1] 陈金勇.一种卫星照相规划软件的可视化设计与实现[J].无线电通信技术,2004,30(6):35-37.
[2] 谷宏志.STK在卫星地面应用系统中的应用[J].无线通信技术,2007,33(3):56-58.
[3] 李冬,唐容富,易东云.对地观测卫星访问区域目标时间窗口快速算法[J].上海航天,2010,27(3):1-5.
[4] 刘晓东.基于MapX的多星协同对对区域目标观测的预处理方法[J].系统工程理论与实践,2010,30(12):2269-2275.
[5] 黄群东,杨芳,赵键.新型敏捷卫星机动中成像模式研究[C]∥第三届高分辨率对地观测学术年会论文集,2014.
[6] 刘晓东.基于空间几何模型的遥感卫星任务分解算法[J].系统工程与电子技术,2011,33(8):1783-1788.
[7] LEMATRE M,VERFAILLIE G,JOUHAUD F,et al.How to Manage the New Generaton of Agile Earth Observation Satellites?[C]∥Proc.of the International Conference on Artifical Intelligence,2000.
[8] 白保存.考虑任务合成的成像卫星调度模型与优化算法研究[D].长沙:国防科学技术大学,2008.
[9] 尹璐.多载荷对地观测卫星目标访问计算及任务调度方法的研究[D].长沙:国防科学技术大学,2012.
[10] 韩丽,张学庆.基于模拟退火的卫星地面站任务规划方法[J].无线电工程,2010,40(9):42-45.
[11] 张超.基于贪婪算法的遥感地面站任务调度技术[J].无线电工程,2011,41( 1):58-60.
[12] 常飞.卫星地面站数传资源配置优化模型与算法研究[D].长沙:国防科学技术大学,2010.
[13] 路帅,孙凯,义余江.敏捷卫星任务调度模型、方法及系统研究[C]∥第二届高分辨率对地观测学术年会,2013.
[14] 阮启明.面向区域目标的成像侦查卫星调度问题研究[D].长沙:国防科学技术大学,2006.
[15] WALTON J.Models for the Management of Satellite Based sensors[D].Cambridge:Massachusetts Institute of Technology,1993.
[16] 刘雄,阮启明,陈英武.卫星全球普查任务规划系统预处理模块的开发[J].计算机仿真,2006,23(7):43-46.
[17] 宗建建,李孟军,姚锋,等.卫星任务规划系统时间窗口模块的设计与实现[J].计算机工程与设计,2005,26(6):1554-1556.
[18] 刘晓东,王鹏,林元,等.敏捷卫星对目标访问信息的计算方法[J].无线电通信技术,2016,42(5):23-26.
[19] 黄群东,杨芳,赵键.敏捷卫星宽幅动态成像姿态调整技术研究[J].航天器工程,2013,22(4):17-22.
[20] 霍庆泽.敏捷卫星任意姿态摄影下的姿态计算模型[J]. Journal of Aerospace Science and Technology,2015,3(3):54-59.
[21] 王淑一,魏春岭,刘其睿.敏捷卫星快速姿态机动方法研究[J].空间控制技术与应用,2011,37(4):36-40.
SatelliteAccessCalculateMethodBasedonAltitudeInformation
ZHAO Ru-zhe1,LIN Yuan2,PENG Hui-xiang1,YUN Jian-sha1,ZHANG Wan-yu3
(1.The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China; 2.BeijingRemoteSensingInformationInstitute,Beijing100192,China; 3.MilitaryRepresentativeOfficeinShijiazhuangDistrict,MilitaryRepresentativeBureauofArmyinBeijing,ShijiazhuangHebei050081,China)
Imaging satellite mission planning is based on access analysis,whose core is to calculate the satellite access information to the target,i.e.,the observation time and observation angle of the satellite to the target.In existing satellite mission control systems,the method of calculating satellite access information usually does not take into account the target altitude information,which makes the calculation of the attitude angle of the target at high altitudes not accurate enough.An improved method of satellite access information calculation based on target altitude information is proposed in this paper.When constructing the space calculation model of satellite and target,this method considers the target altitude information,and then calculates the more accurate observation attitude angle,and makes the satellite after the planning to shoot accurately to the target position.Experimental results show that the algorithm reduces the systematic error and improves the accuracy of satellite observation.
imaging satellite;earth observation;access calculate;altitude information
10.3969/j.issn.1003-3106.2017.12.15
赵汝哲,林元,彭会湘,等.基于高程信息的卫星访问计算方法[J].无线电工程,2017,47(12)67-70,74.[ZHAO Ruzhe,LIN Yuan,PENG Huixiang,et al.Satellite Access Calculate Method Based on Altitude Information[J].Radio Engineering,2017,47(12):67-70,74.]
TP391
A
1003-3106(2017)12-0067-04
2016-12-08
国土资源公益性行业科研专项基金资助项目(201411119)。
赵汝哲男,(1987—),硕士,工程师。主要研究方向:系统工程、航天地面应用。
林元男,(1979—),硕士,高级工程师。主要研究方向:卫星任务管理控制技术、卫星地面应用技术。

