卷到卷制造中基板横向振动研究进展
尹周平, 马 亮, 陈建魁
(华中科技大学数字制造装备与技术国家重点实验室 武汉,430074)
◀专家论坛▶doi:10.16450/j.cnki.issn.1004-6801.2017.05.001
卷到卷制造中基板横向振动研究进展
尹周平, 马 亮, 陈建魁
(华中科技大学数字制造装备与技术国家重点实验室 武汉,430074)
运动基板的横向振动问题已经成为严重限制卷到卷制造效率和质量的关键。详细介绍了卷到卷制造中运动基板横向振动问题的研究概况。讨论了运动基板横向振动的建模方法,以Hamilton原则为例,推导了基板横向振动的控制方程,结合解析求解和数值求解方法,计算横向振动的频率和模态。分析了基板张力、速度、材料特性、中间支撑和外界环境等因素对基板自由振动特性及动态稳定性的影响。研究了基板参数振动特性,考虑基板张力和速度两个主要参数的波动,阐述了基板横向振动被动控制和主动控制方法。联合基板纵向张力控制和侧向纠偏控制,讨论了横向振动控制在卷到卷制造中的工程应用。最后,展望卷到卷制造工程应用中基板横向振动研究的关键问题。
卷到卷制造;运动基板;横向振动;动态特性;振动控制
引 言
卷到卷制造是指柔性基板通过成卷连续的方式进行加工装配的制造技术,基板首先从放卷模块卷出,然后经过多个工艺模块,在柔性基板上进行连续加工,最后成品材料收卷。这种生产方式属于串行过程,包括放卷、加工和收卷3个主要环节,每个工序的输出是下一个工序的输入,其自动化程度高,生产效率高,不仅广泛应用于纸张、印刷产品、纤维、纺织和复合材料等传统材料生产中,而且已成为无线射频识别(radio frequency identification, 简称RFID)标签、有机发光二极管、薄膜太阳能电池和印刷电子等领域理想的制造技术。
通常,具有平、薄、矩形截面形状、较小弯曲刚度等特征的轴向运动材料称为基板。为了获得更高的产量,卷到卷制造中基板以较高的速度输送。由于轴向传输速度的影响,基板不可避免地会沿着与运动速度垂直的方向产生复杂的动力学行为,引起横向振动和噪声,从而严重影响了卷到卷制造的应用效果。比如,在磁带卷绕中,磁带的横向振动会使信号调制失败并加快磁带磨损;在发动机的皮带驱动中,皮带的振动会引起噪声和影响发动机的平稳运转;在印刷或层合过程中,基板的振动及其引起的褶皱会影响产品的套印精度,在柔性电子印刷中通常基板对准精度要求在±10 μm以内,即使较小的振动也有可能引起对准误差,导致较差的印刷质量[1]。
卷到卷制造中随着速度的增加基板运动也会出现失稳现象。在临界速度以上,基板会发生多种动态失稳现象,比如分岔和颤振。基板的横向振动已成为制约卷到卷制造效率和质量的瓶颈,在高速卷绕输送中限制作用更为突出[2]。基板的横向振动动力学分析及控制已成为卷到卷高速输送系统的一个迫切需要解决的问题,其运动动态稳定性的研究有助于确定卷到卷设备设计、制造及使用中安全稳定工作的速度区间,横向振动控制方法的研究能够帮助进一步提升设备运行速度和生产效率。
笔者首先介绍运动基板横向振动的动力学建模和求解方法;其次,讨论基板自由振动特性和参数振动特性研究进展;然后,阐述基板横向振动控制方法及工程应用;最后,展望卷到卷制造中基板横向振动研究的关键问题。
1 动力学建模及求解方法
卷到卷中运动基板动力学方程建模方法通常包括Hamilton原理、D′Alembert原理、虚功原理以及Lagrange方程4种方法[3]。其中,D′Alembert原理是指在基板运动的任一时刻,基板所受的主动力F、约束力FC以及惯性力FI构成平衡力系,即F+FC+FI=0,将运动基板的动力学问题转变成了静力学问题。虚功原理是指外力在系统满足约束条件下的虚位移上所作的虚功总和为零。其中,Hamilton原理[4-6]是最为常用的一种建模方法,它是采用变分的思想来建立方程,即在任意时间段内,基板的动能K,势能U,非有势力做的虚功Wnc和边界传递的虚动量M的变分之和为零,即

(1)
运动的Lagrange方程实质上是改进的Hamiton原理,即

(2)
对于非保守力中的阻尼力,一般采用试验方法获得。


图1 运动基板的物理模型Fig.1 Schematic of the travelling web
依据Hamilton原理[7-9],基板的动能K,势能U,非有势力做的虚功Wnc,和边界传递的虚动量M分别可以表示为
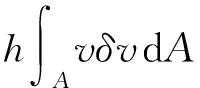
(3)

(4)
(5)

(6)
将式(3)~(6)代入式(1),可以推导出运动基板的动力学方程,即


(7)


(8)


(9)
注意,式(7)和式(8)是仅与面内位移有关的偏微分方程,式(9)是耦合面内位移与面外位移的非线性偏微分方程。如果假设面内平动速度为常数,则上述方程可退化为固定速度下的基板动力学方程。
对于运动基板横向振动的动力学方程通常有两类求解方法:解析解法和数值解法。解析解法主要有小参数摄动法、多尺度法和渐近法等,但是解析解法存在很大的局限性,只能用来求解部分特殊边界条件下的问题,对于受复杂约束基板,一般很难直接求解得到解析解。因此,工程计算中常常采用数值解法来计算基板横向振动的频率及动态响应。目前,比较成熟的数值解法主要有Galerkin方法、有限差分法、微分求积法、有限条法、时域逐渐积分法以及谐波平衡分析法等[3]。其中,Galerkin法[10-12]是解决轴向运动基板横向振动问题的一种很有效的方法,它是加权残值法的一种,采用偏微分方程对应的弱形式,通过选取有限个基函数,将它们叠加,再使结果在求解域内及边界上的积分满足原方程,便可以得到一系列易于求解的线性代数方程,且自然边界条件能够自动满足。Shin等[13]在采用Galerkin方法求解薄膜横向振动方程时,选取面外位移近似函数为

(10)
权函数与近似函数形式相同。
有限差分法[14-16]基本思想是在节点上按适当的数值微分公式把方程中的微商转变成差商,从而把微分方程离散为差分格式,进而求出数值解。Shangguan等[17]采用有限差分法来描述皮带横向振动位移的一阶偏导数和二阶偏导数
(11)
(12)
微分求积法[18-19]的实质就是用域上全部节点的函数值进行加权求和来表示函数及其导数在给定节点处的值,可以将微分方程转变成以节点处的函数值为未知量的一组代数方程组,求解该代数方程,即可得到偏微分方程的数值解为
(13)

这样只要系数确定了,函数在该节点处的各阶导数值就可以用所有节点处的函数值的加权求和来近似替代。微分求积法应用的关键在于节点的选取、边界条件的施加、权系数的确定以及解的收敛性。微分求积法相比有限差分法,只需少量的离散点就可以得到很高的精度,而且迭代的次数也较少。
Newmark方法[20-21]直接对运动方程进行积分,而不进行任何变换,也称为时域逐步积分法,要求时间步长的端点满足微分方程即可,通过平均假设、线性假设、等加速度假设等对时间步长内的系统方程进行曲线拟合,从而求得系统在时域内的动态响应。另外,求解系统动态响应的方法还有振型叠加法和四阶Runge-Kutta方法[22]。
2 卷到卷中基板横向振动
2.1 自由振动
面内平动基板横向振动位移较小时,可以采用线性振动的模型,主要研究线性自由振动的固有频率和模态。Ulsoy等[23]于1982年最早开始关于面内平动薄膜或薄板的横向振动特性研究,分析了基板平动时的动态稳定性。
基板的运动速度对系统的动态特性有很大的影响。通常,基板横向自由振动的特征值是复数形式,其虚部表示自振频率,实部表示幅度。基板在临界速度以下运动时,横向振动都是动态稳定的[12, 24-26],如图2所示,wz(1,1)和wz(2,1)分别为(1,1)阶和(2,1)阶模态特征值,随着基板运动速度的不断增大,基板振动稳定性可以分3个状态。状态1:所有特征值的实部全为负数或零,基板横向振动是动态稳定的。状态2:有一个特征值的虚部变为零,同时有特征值出现正实部,基板振动开始不稳定,出现分岔现象,此时基板的运动速度称为临界速度。状态3:有一个或多个特征值出现正实部和正虚部,基板开始更为剧烈的振动,出现颤振现象,此时基板的运动速度称为颤振速度。

图2 横向振动频率Fig.2 The natural frequencies of transverse vibration
Shin等[27-28]利用Hamilton原则推导出基板面内、面外运动的动力学方程,在对辊边界处考虑两种边界条件:一种是基板在边界处沿y向固定,不能自由移动;另外一种是基板在边界处沿y向无摩擦,可自由移动[29],并结合Galerkin方法,计算了薄膜横向振动的自振频率和模态形状,研究了平动速度、长宽比和边界条件对横向振动稳定性的影响。Luo等[30]分析了高速运动薄板的横向振动位移和屈曲稳定性。Wang等[20]基于Kirchhoff-Love板理论和Hamilton原则,建立了任意变长度的板的运动方程,利用Galerkin方法和Newmark方法从频域和时域分别研究了板的稳定性和动态响应,分析了面内平动和弯曲变形的耦合效应,结果表明平动速度和板长宽比对面外振动频率和稳定性有很大影响。
从放卷到收卷,基板在输送过程中通常在中间由多个支撑辊作用,辊子的支撑作用直接影响了运动基板的动态特性。Wu等[31]分析了造纸印刷中,纸张输送时在中间多辊支撑下的横向振动特性,通过Laplace变换,得到了振动频率方程,研究了振动频率与速度、张力、支撑刚度和支撑位置的关系,为造纸印刷过程中改进结构设计和提高稳定性提供了理论基础和有效的方法。Lü等[32]基于经典的Kirchhoff板理论,结合状态空间的方法,分析了在刚性线支撑和移动弹性基底支撑下的大跨距连续矩形板的自由振动频率。如图3所示,Banichuk等[33]采用解析的方法研究了无限个弹性支撑下的运动基板的动态稳定性,基板的横向振动位移由一个包含离心力、面内应力、弯曲项和弹性支承力的四阶微分方程表示。Ghayesh等[34]研究了中间受弹性支撑下和分布式简谐激振力的轴向运动基板的横向和纵向耦合振动特性。Bagdatli等[35]采用多尺度分析方法研究了左右边界简支、中间有一弹性支撑的变速运动欧拉梁的横向振动特性,讨论了运动速度和中间支撑位置对基板运动稳定区间的影响。

图3 弹性支撑下的轴向运动梁Fig.3 Axially moving beam supported by elastic supports
基板卷到卷输送过程中,由于支撑辊子的不平行和对辊驱动力的分布不均,导致基板两端承受的张力并不是均匀分布的,研究非均匀张力分布作用下的基板横向振动特性具有一定的实际意义。Banichuk等[36]分析了线性张力分布作用下的面内平动基板的振动特性,建立了一个考虑离心力、面内张力、弹性变形力和惯性力的偏微分方程,通过数值方法,证明了张力分布的不均匀可以很大程度上降低基板失稳的临界速度,即使很小的张力不均匀程度都可以对分岔形状产生很大的影响。王砚等[37]分析了两端非均匀分布张力作用下的运动矩形薄膜的动力特性及稳定性,建立了非均匀张力作用下运动薄膜的计算模型,采用微分求积法,推导系统的复特征值方程,结合数值计算,分析了薄膜长宽比、速度和张力变化系数对系统复频率和薄膜动态行为的影响。
目前,复合材料被广泛应用在实际工程制造中,比如动力传输带、复合板等,这种基板不再是传统的各向同性材料,往往具有各向异性,因此针对轴向运动复合基板振动分析中有必要考虑材料的各向异性。Yang等[38]研究了正交各向异性矩形复合板的振动特性,分别利用Galerkin方法和微分求积法求解复合板的振动频率,发现面内振动的频率要远远大于面外振动频率,因此工程实际中仅考虑平板面外振动特性是合理的。Jaberzadeh等[12]采用无网格Galerkin方法研究了轴向运动正交或斜交各向异性薄板自由振动特性,分析了辊子不平行角度和中间弹性支撑对薄板自由振动频率的影响。Hatami等[39]利用一种精确的和半解析的有限条带法分析了轴向运动层合基板的自由振动问题,发现随着轴向运动速度的不断增加,复合板自由振动的频率在不断减小,同时复合板边界受力和长宽比也会对频率产生影响。
运动基板与周围环境介质之间的相互作用是影响卷到卷中平动基板稳定性的一个重要因素,当忽略基板与空气之间的相互作用时,基板运动失稳的临界速度要比实际临界速度高很多。Banichuk等[40]建立了一个包含离心力、空气作用力、张力、弯曲力的积分微分方程,其中空气作用反力是位移的解析函数,采用数值方法求解了基板在真空中和在流体相互作用下的运动失稳临界速度,对比发现基板运动失稳临界速度受周围流体作用影响较大。随后,Banichuk等[41]用解析方法研究了平动板与周围理想流体相互作用下的动态响应,并假设基板是圆柱变形。
如何对基板材料进行建模是工程实际中一个重要的问题,随着材料技术的不断进步,卷到卷中基板开始采用金属或陶瓷增强复合材料、聚合物材料等,这些非纯弹性材料不再满足传统的胡克定律,解决该问题的有效途径就是在建模中考虑材料的黏弹性。同时,随着黏弹性材料的引入,使得卷到卷输送中基板横向振动的动力学行为也更加复杂。
Marynowski等[7]提出用两参数的Kelvin-Voigt和四参数的Burers模型来表示面内平动黏弹性板,分析了内部阻尼和平动速度对平动板动态稳定性的影响,指出对于内部阻尼较小的黏弹性板,两种模型计算结果相近,对于较大内部阻尼的黏弹性板,Burgers模型更接近真实情况。Chen等[42]使用Kelvin模型分析了黏弹性梁和黏弹性板的非线性振动特性,其中应力与应变的关系表示为
σx=E(εx+α(εx,t+Γεx,x))
(14)
其中:E为弹性模量;α为黏性系数。
Marynowski[43]提出用一个二维流变单元模型来模拟面内平动黏弹性板,结合流变模型以及板理论,用Galerkin数值方法研究了造纸中的横向振动现象。Chen等[44-46]用Kelvin模型来模拟粘弹性梁的材料特性,研究了阻尼系数、平动速度和张力对运动稳定性的影响。Zhou等[16, 47-48]研究了变厚度粘弹性板的振动特性,利用Kelvin模型,考虑黏弹性板沿y向厚度是非均匀的,使用微分求积法验证了板长宽比、厚度变化系数、平动速度对板的动力特性和稳定性的影响。
Hatami等[49]分析了面内平动黏弹性板的自由振动特性,采用了精确的有限条方法,其中材料的线性黏弹性采用积分形式,其公式为

(15)
其中:σij为应力函数;εkl为应变函数;Rijkl为四阶松弛函数。
2.2 参数振动
生产实际中,运动系统参数的周期性变化可能会导致基板发生剧烈的横向振动,在卷到卷制造中,这种参数的变化主要体现在基板面内张力的变化和基板运动速度的变化。
Marynowski等[9, 50]研究了在两端受时变张力作用下的黏弹性基板的非线性振动行为,表达式为
P=P0+P1cos(wt)
(16)
其中:P为在稳态张力P0基础上周期性波动张力;P1为波动幅值;w为波动频率。
采用Galerkin方法和四阶Runge-Kutta方法来求解非线性偏微分方程,并分析了平动速度、张力的波动幅值以及系统内部阻尼对基板横向振动动力学行为的影响。
Yang等[51]提出了一种基于能量的控制方法来抑制变张力、变速度、存在干扰下的轴向运动梁的横向振动,其中速度变化产生的惯性力导致基板面内张力的改变。
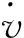
(17)
其中:e = 0代表水平方向运动的梁,e = 1代表竖直方向运动的梁;g为重力加速度;T0为初始张力。
在梁变速运动过程中,加速阶段轴向力可能是拉力,减速运动时轴向力可能会变成压力。Lee等[52]研究了四边自由的面内加速运动薄板的横向振动动力学行为,采用Bolotin方法分析面内张力和平动加速度摄动在不同组合类型下基板运动失稳的区域。Tang等[53-55]讨论了轴向加速运动黏弹性梁或板的主参数共振、内共振以及非线性振动,其中基板所承受张力的变化来源于基板运动加速度。Lü等[56]采用多尺度分析方法研究了边界承受简谐张力变化的轴向运动叠层梁的非线性参数共振现象。Lengoc等[57-58]研究了面内边界受周期性变化载荷作用下系统振动的失稳区域。
Pakdemirli等[59-60]研究了轴向变速运动梁的稳定性,梁的运动速度是时变的,表示为
v=v0+εv1sin(ωt)
(18)
其中:εv1为波动幅值;ω为波动频率。
Chen等[44, 46]分析了轴向加速运动黏弹性梁的横向振动稳定性以及非线性振动特性,轴向运动速度均是在一个稳定速度基础上作简谐变化。
Bagdatl等[35]研究了具有中间固定支撑的轴向变速运动欧拉梁的横向振动动力学行为,在动力学方程中引入非线性项,分析了当速度波动频率等于自振频率两倍时的主参数共振现象,给出了基板运动的稳定区域和失稳区域。Tang等[8, 61]采用多尺度分析方法,研究了面内应力作用下的平动黏弹性薄板的非线性参数共振和内部共振,分析了平动速度、平动速度波动幅值、黏弹性系数和非线性系数对稳态响应的影响。Wu等[62]采用微分求积法研究了纸张生产中沿轴向变速运动纸张的参数振动和动态稳定性,利用Runge-Kutta方法确定了纸张运动的稳定速度区域。
王波等[63]提出了一种结合微分求积法研究非线性变速运动黏弹性梁的混杂边界条件的方法。刘金堂等[64]分析了变速运动正交各向异性薄板横向振动的动态稳定性,建立薄板横向振动的偏微分方程,结合多尺度法,利用可解性边界条件得到次谐波共振和组合共振的稳定边界,并用数值算例分析平动速度、激励幅值等参数对稳定性边界的影响。
3 横向振动抑制方法
早期基板横向振动控制的研究主要集中在采用被动的增加阻尼或有效刚度来实现,这种控制方法由于不需要外部能量输入,结构简单可靠,易于维护,在工程领域中得到广泛应用。随着基板运行速度的不断提高,对基板振动特性、对产品的质量要求更加严格,这种被动的控制方法存在一定的局限,为了适应更加复杂的条件,就需要通过施加外力来实现振动的主动控制。主动控制算法主要包括直接速度反馈控制[65]、频域传递函数控制[66]、主动波控制[67]、使用Lyapunov的边界控制[68]和自适应控制等[69]。另外,卷到卷中振动控制大多采用的都是点控制而不是分布式控制。虽然分布式控制方法可能会产生更好的控制效果,但是由于分布式控制方法需要分布的信号反馈和控制力,实际工程中很难实现。
Fung等[68, 70-71]研究了在右边边界处施加一个质量-阻尼-弹簧控制器的轴向运动弦线的横向振动控制问题。如图4所示,该控制器包含质量块m, 系数为dm的黏性阻尼器和刚度为km的弹簧,控制器输入为Fc,弦线运动速度为c,横向振动位移为v(x,t),然后分别采用了最优边界控制、自适应边界控制和使用Lyapunov函数的边界控制方法进行横向振动控制。所施加的外界力依赖于弦线右边界处的倾斜角、速度和位移,依据机械能耗散和群论证明了系统的指数稳定性,得到了最低反馈增益,最后通过有限差分的方法验证了所提出的各种控制方法的有效性。

图4 采用质量-阻尼-弹簧控制器的轴向运动弦线系统Fig.4 An axially moving string system with the mass damper-spring (MDS) controller
Zhu等[72]采用结合Lyapunov稳定判据的边界控制策略来对任意变化长度的轴向运动梁进行振动能量的消散,分析了轴向速度变化对张力的影响,在最优控制增益下,轴向运动梁在伸出或缩回时都能保持运动的稳定性。
Yang等[73]研究了张力随时间和空间在不断变化并存在未知边界扰动的运动弦线的横向振动抑制方法,系统如图5所示。弦线运动速度为vs,两端张力为Ts,横向振动位移为w(x,t),在弦线中间施加了一个液压托辊驱动器,其质量和阻尼分别为mc和dc,驱动器将弦线分为受控区域与未受控区域,未受控区域看作扰动输入,通过Lyapunov方法设计了鲁棒边界控制策略来进行受控区域的横向振动控制。后来,Yang等[74]又针对变速运动梁的振动控制研究了基于Lyapunov方法的边界控制策略。

图5 采用液压驱动器的轴向运动弦线振动控制布局Fig.5 One control-oriented schematic of the axially moving string with a hydraulic actuator
由于自适应边界控制方法一般依赖于轴向运动基板和外加驱动器的参数值,Nguyen等[75]提出了一种在变张力和边界干扰下可以补偿弦线自身和边界控制器不确定性的鲁棒自适应边界控制方法。
Chao等[76]采用智能控制策略来抑制轴向运动弦线的横向振动,提出了模糊滑模控制方法和模糊神经网络控制方法,在弦线右边边界位置处施加一个质量-阻尼-弹簧控制器,通过运动弦线和控制器系统动态耦合产生的驱动力来抑制横向振动。其中模糊滑模控制方法的优势是可以计算系统的瞬态响应,而模糊神经网络控制方法能够实现在线学习。
张伟等[77-80]研究了轴向运动弦线和控制器组成的耦合系统的横向振动控制问题,采用Lyapunov方法、自适应方法、能量方法和线性反馈控制方法,凭借作用在控制器上的外界力对系统受控区域进行主动控制。李志军等[81]在以上基础上,考虑了作动器由于运动等其他因素造成其模型含有的参数具有不确定性,为了改善控制系统的鲁棒性,在鲁棒的二次镇定控制基础上,设计了状态反馈的H∞控制。
以上控制方法主要将控制对象作为弦线和梁,在针对轴向运动薄膜的横向振动控制研究中,刘定强等[82]建立了薄膜横向振动抑制的状态空间方程,结合次最优控制方法和直接速度反馈法,在匀速条件下对薄膜进行了横向振动控制。首先计算最优状态控制的常反馈增益,接着计算次最优情况下反馈增益,并通过Matlab数值计算验证该方法的有效性。
武吉梅等[83]建立了不同边界下、考虑弯曲刚度的轴向运动薄膜的动力学方程,采用有限差分法,将振动微分方程离散,采用次最优控制方法,对四边简支、对边简支对边自由两种边界条件下的振动进行主动控制,在短时间迅速、有效地使薄膜振动强度衰减趋近于零。计算结果说明,作动器作用在固定点时,对于四边简支下的薄膜振动控制效果较好;作动器作用在不同位置点时,这两种边界条件下均是作用在中心点时的控制效果较好。卷到卷制造中,部分基板表面要求不能有外力作用,否则会影响基板表面的质量,因此这种基板横向振动控制方案中不能再施加外界控制力。 Nguyen等[2, 84-85]提出了一种新的抑制平动薄膜横向振动的方法,通过Galerkin方法,将振动的偏微分方程离散成为一系列常微分方程,并转变成状态空间的形式,面内平动薄膜的振动能量表示成状态变量的二次型,利用共轭梯度的优化方法生成一条期望的速度曲线,使平动薄膜在按照这个速度曲线运动时,振动能量减弱地最快。结合数值计算,证明了所提出控制方法的有效性。如图6所示,在采用设计的速度曲线的情况下,振动能量和基板横向振动位移在速度为零时已完全接近为零,而不采用振动控制仅靠薄膜自身粘性阻尼力的情况下,薄膜振动能量和横向振动位移需要很长的时间才能收敛到零,严重影响设备生产效率。Jabbar等[6]在Nguyen研究的基础上,引入材料黏弹性特性和张力约束条件,在设计基板运动速度曲线时要求张力变化在许可范围之内。

图6 振动能量和横向位移对比,采用控制方法(实线)和未采用控制方法(虚线)Fig.6 Comparison of the vibration energy and the transverse displacement; controlled (solid line) versus uncontrolled (dotted line)
4 工程应用
卷到卷制造广泛应用在RFID标签、有机发光二极管、薄膜太阳能、印刷电子等柔性电子制造领域。目前,已经开发出多种集成卷到卷制造技术的生产装备。为了实现高分辨率、高效、高可靠地卷到卷制造,必须保证基板能够稳定、精确的输送,其中影响运动基板动态稳定性的主要因素有基板张力、基板运动速度以及基板侧向偏移,这些因素的变化会引起基板横向振动,导致基板运动失稳,必须对基板张力、速度和侧向位移进行精确控制。
图7所示为RFID标签生产设备,包括基板输送、点胶、贴装、热压和检测模块,其中基板输送模块是其他各个模块能够顺利完成任务的前提和基础。为了保证点胶、贴片、热压和检测正常工作,实现芯片与线圈的倒装互连,必须保证柔性基板稳定的输送,因此需要对基板实施张力稳定控制、位置控制和纠偏控制[86-89]。

图7 RFID标签封装设备Fig.7 RFID tags packaging equipment
该设备中为实现张力稳定控制,在放卷电机之后采用浮棍,卷绕过程中,浮棍会随基板张力的变化而上下移动[90]。收放卷电机采用磁粉离合器驱动,利用张力传感器实时检测基板收放卷区域张力的变化,根据反馈信号调整磁粉离合器控制电流,实现恒张力控制[91];在基板加工区域采用张力-位置混合控制方法,将检测到的张力信号作为驱动电机位置补偿,利用驱动电机转动位移的变化实现张力和位置混合控制[92]。同时为了实现基板侧向偏移控制,在基板输送多个区域安装纠偏控制器,实现基板侧向位置的实时监测和控制[93]。
图8所示为卷到卷刻蚀系统[94],将传统的平板印刷、真空涂层和纳米压印等图案化工艺与卷到卷技术进行融合,采用了精密光学测量系统,在柔性基板上可实现连续、高分辨率图案化,其中分辨率最高达10 μm,层间套准精度最高达±2.5 μm。

图8 卷到卷刻蚀系统Fig.8 Roll-to-roll lithography system

图9 显示器件卷到卷制造流程Fig.9 Roll-to-roll manufacturing of display parts
图9所示为柔性显示器件卷到卷制造流程,底层薄膜经过苯胺印制、烘干、真空喷射和凹版印刷等操作后与顶层薄膜再通过对辊进行不同薄膜的层合,在生产过程中对各层薄膜实施张力控制、振动抑制和纠偏控制等抑制薄膜变形,保证薄膜基板输送中的稳定性,实现多层薄膜的高精度加工定位和准确层合[95]。
5 展 望
运动基板横向振动分析与控制已成为卷到卷制造研究的关键问题,笔者重点讨论运动基板横向振动建模与求解方法、自由振动特性、参数振动特性、振动控制方法以及工程应用的若干重要研究进展。为了实现基板更高速、更稳定地传输,卷到卷制造中运动基板的横向振动还存在以下问题需进一步深入研究:
1) 卷到卷制造工程应用中,基板往往具有材料和几何非线性,并受复杂约束和一定的时变激励,如何更精确地对基板进行建模求解仍需进一步探索。
2) 考虑非线性因素、复杂约束和时变激励的运动基板横向振动控制问题的研究刚刚起步,数学建模中对基板非线性振动模型均有一定的简化,要求边界控制、非边界控制或智能控制等方法具有更高的自适应性和鲁棒性。
3) 目前,对运动基板的横向振动特性及控制方法的研究主要集中在理论推导与数值计算,在实验研究方面主要针对简支结构或悬臂结构,未考虑基板运动带来的影响。针对运动基板横向振动的实验研究还有待进一步探索。
[1] Seshadri A, Pagilla P R, Lynch J E. Modeling print registration in roll-to-roll printing presses[J]. Journal of Dynamic Systems, Measurement, and Control, 2013, 135(3): 31016-1-31016-11.
[2] Nguyen Q C, Hong K S. Simultaneous control of longitudinal and transverse vibrations of an axially moving string with velocity tracking[J]. Journal of Sound and Vibration, 2012, 331(13): 3006-3019.
[3] 杨翠屏. 非线性地基上四边自由矩形薄板的非线性动力学分析[D]. 长沙: 长沙理工大学, 2013.
[4] Park S, Yoo H H, Chung J. Vibrations of an axially moving beam with deployment or retraction[J]. AIAA Journal, 2012, 51(3): 686-696.
[5] Tang Youqi, Zhang Dengbo, Gao Jiaming. Parametric and internal resonance of axially accelerating viscoelastic beams with the recognition of longitudinally varying tensions[J]. Nonlinear Dynamics, 2016, 83(1-2): 401-418.
[6] Jabbar K A, Pagilla P R. Optimal velocity profile design for transport of viscoelastic webs in roll-to-roll manufacturing[C]∥Proceedings of 2016 American Control Conference.[S.l.]: IEEE, 2016: 1729-1734.
[7] Marynowski K, Kapitaniak T. Kelvin-Voigt versus Bürgers internal damping in modeling of axially moving viscoelastic web[J]. International Journal of Non-Linear Mechanics, 2002, 37(7): 1147-1161.
[8] Tang Youqi, Chen Liqun. Parametric and internal resonances of in-plane accelerating viscoelastic plates[J]. Acta Mechanica, 2012, 223(2): 415-431.
[9] Marynowski K. Non-linear vibrations of an axially moving viscoelastic web with time-dependent tension[J]. Chaos, Solitons & Fractals, 2004, 21(2): 481-490.
[10] Zhang Guoce, Ding Hu, Chen Liqun, et al. Galerkin method for steady-state response of nonlinear forced vibration of axially moving beams at supercritical speeds[J]. Journal of Sound and Vibration, 2012, 331(7): 1612-1623.
[11] Ding Hu, Chen Liqun. Galerkin methods for natural frequencies of high-speed axially moving beams[J]. Journal of Sound and Vibration, 2010, 329(17): 3484-3494.
[12] Jaberzadeh E, Azhari M, Boroomand B. Free vibration of moving laminated composite plates with and without skew roller using the element-free Galerkin method[J]. Iranian Journal of Science and Technology, Transactions of Civil Engineering, 2014, 38(C2): 377-393.
[13] Shin C, Chung J, Kim W. Dynamic characteristics of the out-of-plane vibration for an axially moving membrane[J]. Journal of Sound and Vibration, 2005, 286(4-5): 1019-1031.
[14] Yang Xiaodong, Zhang Wei, Chen Liqun, et al. Dynamical analysis of axially moving plate by finite difference method[J]. Nonlinear Dynamics, 2012, 67(2): 997-1006.
[15] Ding Hu, Chen Liqun. Stability of axially accelerating viscoelastic beams: multi-scale analysis with numerical confirmations[J]. European Journal of Mechanics-A/Solids, 2008, 27(6): 1108-1120.
[16] Zhou Yinfeng, Wang Zhongmin. Vibrations of axially moving viscoelastic plate with parabolically varying thickness[J]. Journal of Sound and Vibration, 2008, 316(1): 198-210.
[17] Shangguan Wenbin, Feng Xiao, Lin Haoting, et al. A calculation method for natural frequencies and transverse vibration of a belt span in accessory drive systems[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2013, 227(10): 2268-2279.
[18] Liew K M, Huang Y Q, Reddy J N. Vibration analysis of symmetrically laminated plates based on FSDT using the moving least squares differential quadrature method[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(19): 2203-2222.
[19] Liu Jintang, Fu Li, Yang Xiaodong, et al. A differential Quadrature out-of-plane vibration analysis of axially moving thin plates[C]∥Chinese Control and Decision Conference (CCDC). [S.l.]:IEEE, 2011: 3335-3338.
[20] Wang Lihua, Hu Zhengdong, Zhong Zheng. Dynamic analysis of an axially translating plate with time-variant length[J]. Acta Mechanica, 2010, 215(1-4): 9-23.
[21] Banichuk N, Jeronen J, Ivanova S, et al. Analytical approach for the problems of dynamics and stability of a moving web[J]. Journal of Structural Mechanics, 2015, 48(3): 136-163.
[22] 杨迪. 轧制过程中轴向运动矩形薄板的非线性振动研究[D]. 秦皇岛: 燕山大学, 2013.
[23] Ulsoy A G, Mote J C D. Vibration of wide band saw blades[J]. Journal of Engineering for Industry, 1982, 104(1): 71-78.
[24] Ghayesh M H, Yourdkhani M, Balar S, et al. Vibrations and stability of axially traveling laminated beams[J]. Applied Mathematics and Computation, 2010, 217(2): 545-556.
[25] Tang Youqi, Chen Liqun, Yang Xiaodong. Natural frequencies, modes and critical speeds of axially moving Timoshenko beams with different boundary conditions[J]. International Journal of Mechanical Sciences, 2008, 50(10-11): 1448-1458.
[26] Wang Yuefang, Huang Lihua, Liu Xuetao. Eigenvalue and stability analysis for transverse vibrations of axially moving strings based on Hamiltonian dynamics[J]. Acta Mechanica Sinica, 2005, 21(5): 485-494.
[27] Shin C, Chung J, Yoo H H. Dynamic responses of the in-plane and out-of-plane vibrations for an axially moving membrane[J]. Journal of Sound and Vibration, 2006, 297(3-5): 794-809.
[28] Shin C, Chung J, Yoo H H. Dynamic responses of the in-plane and out-of-plane vibrations for an axially moving membrane[J]. Journal of Sound and Vibration, 2006, 297(3): 794-809.
[29] Shin C, Kim W, Chung J. Free in-plane vibration of an axially moving membrane[J]. Journal of Sound and Vibration, 2004, 272(1-2): 137-154.
[30] Luo A C J, Hamidzadeh H R. Equilibrium and buckling stability for axially traveling plates[J]. Communications in Nonlinear Science and Numerical Simulation, 2004, 9(3): 343-360.
[31] Wu Jimei, Wang Zhongmin, Wu Qiuming, et al. Transverse vibration characteristics of a paper web with multi-roller supports[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2009, 28(2): 133-144.
[32] Lü C F, Lee Y Y, Lim C W, et al. Free vibration of long-span continuous rectangular Kirchhoff plates with internal rigid line supports[J]. Journal of Sound and Vibration, 2006, 297(1-2): 351-364.
[33] Banichuk N, Ivanova S, Jeronen J, et al. Periodic spectral instability analysis of axially moving beam with elastic supports[J]. Journal of Structural Mechanics, 2014, 47(1): 1-16.
[34] Ghayesh M H, Amabili M, Paidoussis M P. Nonlinear vibrations and stability of an axially moving beam with an intermediate spring support: two-dimensional analysis[J]. Nonlinear Dynamics, 2012, 70(1): 335-354.
[35] Bagˇdatli S M, Özkaya E, Öz H R. Dynamics of axially accelerating beams with an intermediate support[J]. Journal of Vibration and Acoustics, 2011, 133(3): 31013-1-31013-10.
[36] Banichuk N, Jeronen J, Neittaanmäki P, et al. Theoretical study on travelling web dynamics and instability under non-homogeneous tension[J]. International Journal of Mechanical Sciences, 2013, 66(1): 132-140.
[37] 王砚,聂子恒,武吉梅,等. 非均匀张力作用下运动薄膜的稳定性研究[J]. 西安理工大学学报, 2016, 32(1): 58-62.
Wang Yan, Nie Ziheng, Wu Jimei, et al. The study of stability of the moving membrane under non-uniform tension[J]. Journal of Xi' an University of Technology, 2016, 32(1): 58-62. (in Chinese)
[38] Yang Xiaodong, Chen Liqun, Zu J W. Vibrations and stability of an axially moving rectangular composite plate[J]. Journal of Applied Mechanics, 2011, 78(1): 11018-1-11018-11.
[39] Hatami S, Azhari M, Saadatpour M M. Free vibration of moving laminated composite plates[J]. Composite Structures, 2007, 80(4): 609-620.
[40] Banichuk N, Jeronen J, Neittaanmäki P, et al. Static instability analysis for travelling membranes and plates interacting with axially moving ideal fluid[J]. Journal of Fluids and Structures, 2010, 26(2): 274-291.
[41] Banichuk N, Jeronen J, Neittaanm K P, et al. Dynamic behaviour of an axially moving plate undergoing small cylindrical deformation submerged in axially flowing ideal fluid[J]. Journal of Fluids and Structures, 2011, 27(7): 986-1005.
[42] Chen Liqun, Tang Youqi, Lim C W. Dynamic stability in parametric resonance of axially accelerating viscoelastic Timoshenko beams[J]. Journal of Sound and Vibration, 2010, 329(5): 547-565.
[43] Marynowski K. Two-dimensional rheological element in modelling of axially moving viscoelastic web[J]. European Journal of Mechanics - A/Solids, 2006, 25(5): 729-744.
[44] Chen Liqun, Yang Xiaodong. Transverse nonlinear dynamics of axially accelerating viscoelastic beams based on 4-term Galerkin truncation[J]. Chaos, Solitons & Fractals, 2006, 27(3): 748-757.
[45] Chen Liqun, Yang Xiaodong. Stability in parametric resonance of axially moving viscoelastic beams with time-dependent speed[J]. Journal of Sound and Vibration, 2005, 284(3): 879-891.
[46] Chen Liqun, Yang Xiaodong, Cheng Changjun. Dynamic stability of an axially accelerating viscoelastic beam[J]. European Journal of Mechanics-A/Solids, 2004, 23(4): 659-666.
[47] Zhou Yinfeng, Wang Zhongmin. Transverse vibration characteristics of axially moving viscoelastic plate[J]. Applied Mathematics and Mechanics, 2007, 28(2): 209-218.
[48] Zhou Yinfeng, Wang Zhongmin. Dynamic behaviors of axially moving viscoelastic plate with varying thickness[J]. Chinese Journal of Mechanical Engineering, 2009, 22(2): 276-281.
[49] Hatami S, Ronagh H R, Azhari M. Exact free vibration analysis of axially moving viscoelastic plates[J]. Computers & Structures, 2008, 86(17-18): 1738-1746.
[50] Marynowski K, Kapitaniak T. Zener internal damping in modelling of axially moving viscoelastic beam with time-dependent tension[J]. International Journal of Non-Linear Mechanics, 2007, 42(1): 118-131.
[51] Yang K J, Hong K S, Matsuno F. Energy-based control of axially translating beams: varying tension, varying speed, and disturbance adaptation[J]. IEEE Transactions on Control Systems Technology, 2005, 13(6): 1045-1054.
[52] Lee H P, Ng T Y. Dynamic stability of a moving rectangular plate subject to in-plane acceleration and force perturbations[J]. Applied Acoustics, 1995, 45(1): 47-59.
[53] Chen Liqun, Tang Youqi. Combination and principal parametric resonances of axially accelerating viscoelastic beams: Recognition of longitudinally varying tensions[J]. Journal of Sound and Vibration, 2011, 330(23): 5598-5614.
[54] Tang Youqi, Chen Liqun, Zhang Haijuan, et al. Stability of axially accelerating viscoelastic Timoshenko beams: recognition of longitudinally varying tensions[J]. Mechanism and Machine Theory, 2013, 62(1): 31-50.
[55] Chen Liqun, Tang Youqi, Zu J W. Nonlinear transverse vibration of axially accelerating strings with exact internal resonances and longitudinally varying tensions[J]. Nonlinear Dynamics, 2014, 76(2): 1443-1468.
[56] Lü Haiwei, Li Yinghui, Li Liang, et al. Transverse vibration of viscoelastic sandwich beam with time-dependent axial tension and axially varying moving velocity[J]. Applied Mathematical Modelling, 2014, 38(9-10): 2558-2585.
[57] Lengoc L, Mccallion H. Wide bandsaw blade under cutting conditions: Part I: Vibration of a plate moving in its plane while subjected to tangential edge loading[J]. Journal of Sound and Vibration, 1995, 186(1): 125-142.
[58] Lengoc L, Mccallion H. Wide bandsaw blade under cutting conditions: Part II: Stability of a plate moving in its plane while subjected to parametric excitation[J]. Journal of Sound and Vibration, 1995, 186(1): 143-162.
[59] Öz H R, Pakdemirli M, Boyaci H. Non-linear vibrations and stability of an axially moving beam with time-dependent velocity[J]. International Journal of Non-Linear Mechanics, 2001, 36(1): 107-115.
[60] Tang Youqi, Chen Liqun. Stability analysis and numerical confirmation in parametric resonance of axially moving viscoelastic plates with time-dependent speed[J]. European Journal of Mechanics - A/Solids, 2013, 37(1): 106-121.
[61] Tang Youqi, Chen Liqun, Yang Xiaodong. Parametric resonance of axially moving Timoshenko beams with time-dependent speed[J]. Nonlinear Dynamics, 2009, 58(4): 715-724.
[62] Wu Jimei, Wu Qiumin, Ma Li'e, et al. Parameter vibration and dynamic stability of the printing paper web with variable speed[J]. Low Frequency Noise, Vibration and Active Control, 2010, 29(4): 281-291.
[63] 王波,陈立群. 微分求积法处理轴向变速黏弹性梁混杂边界条件[J]. 振动与冲击, 2012, 31(5): 87-91.
Wang Bo, Chen Liqun. Treating hybrid boundary condition of an axially accelerating viscoelastic beam via a differential quadrature scheme[J]. Journal of Vibration and Shock, 2012, 31(5): 87-91. (in Chinese)
[64] 刘金堂,杨晓东,张宇飞,等. 变速轴向运动正交各向异性板横向振动的直接多尺度分析[J]. 机械强度, 2010, 32(4): 531-535.
Liu Jintang, Yang Xiaodong, Zhang Yufei, et al. Direct multiscale analysis of transverse vibration for an axially accelerating orthotropic plate[J]. Journal of Mechanical Strength, 2010, 32(4): 531-535. (in Chinese)
[65] Yang Bingen. Vibration control of gyroscopic systems via direct velocity feedback[J]. Journal of Sound and Vibration, 1994, 175(4): 525-534.
[66] Yang K J, Hong K S, Matsuno F. Robust boundary control of an axially moving string by using a PR transfer function[J]. IEEE Transactions on Automatic Control, 2005, 50(12): 2053-2058.
[67] Nguyen Q C, Ngo Q H, Hong K S. Active vibration control of an axially moving beam using varying velocity method[C]∥ICCAS-SICE International Joint Conference. [S.l.]: IEEE, 2009: 287-292.
[68] Fung R F, Tseng C C. Boundary control of an axially moving string via Lyapunov method[J]. Journal of Dynamic Systems, Measurement, and Control, 1999, 121(1): 105-110.
[69] He Wei, Ge S S. Robust adaptive boundary control of a vibrating string under unknown time-varying disturbance[J]. IEEE Transactions on Control Systems Technology, 2012, 20(1): 48-58.
[70] Fung Rongfong, Chou Jyhhorng, Kuo Yulung. Optimal boundary control of an axially moving material system[J]. Journal of Dynamic Systems, Measurement, and Control, 2002, 124(1): 55-61.
[71] Fung Rongfong, Wu Jinnwen, Lu Paiyat. Adaptive boundary control of an axially moving string system[J]. Journal of Vibration and Acoustics, 2002, 124(3): 435-440.
[72] Zhu Weidong, Ni Jun, Huang Jie. Active control of translating media with arbitrarily varying length[J]. Journal of Vibration and Acoustics, 2001, 123(3): 347-358.
[73] Yang K J, Hong K S, Matsuno F. Robust adaptive boundary control of an axially moving string under a spatiotemporally varying tension[J]. Journal of Sound and Vibration, 2004, 273(4): 1007-1029.
[74] Yang K J, Hong K S, Matsuno F. Boundary control of a translating tensioned beam with varying speed[J]. IEEE/ASME Transactions on Mechatronics, 2005, 10(5): 594-597.
[75] Nguyen Q C, Hong K S. Asymptotic stabilization of a nonlinear axially moving string by adaptive boundary control[J]. Journal of Sound and Vibration, 2010, 329(22): 4588-4603.
[76] Chao P C, Lai Chengliang. Boundary control of an axially moving string via fuzzy sliding-mode control and fuzzy neural network methods[J]. Journal of Sound and Vibration, 2003, 262(4): 795-813.
[77] 张伟,陈立群. 轴向运动弦线横向振动的线性反馈控制[J]. 应用力学学报, 2006, 23(2): 242-245.
Zhang Wei, Chen Liqun. Transverse vibration control of axially moving string system by linear backward[J]. Chinese Journal of Applied Mechanics, 2006, 23(2): 242-245. (in Chinese)
[78] 张伟,陈立群. 轴向运动弦线横向振动控制的自适应方法[J]. 机械工程学报, 2006, 42(4): 96-100.
Zhang Wei, Chen Liqun. Transverse vibration control of an axially moving string system by adaptive method[J]. Chinese Journal of Mechanical Engineering, 2006, 42(4): 96-100. (in Chinese)
[79] 张伟,陈立群. 轴向运动弦线横向振动的控制:能量方法[J]. 机械强度, 2006, 28(2): 201-204.
Zhang Wei, Chen Liqun. Transverse vibration control of an axially moving string system: energy method[J]. Journal of Mechanical Strength, 2006, 28(2): 201-204. (in Chinese)
[80] 张伟,陈立群. 轴向运动弦线横向振动控制的Lyapunov方法[J]. 控制理论与应用, 2006, 23(4): 531-535.
Zhang Wei, Chen Liqun. Transverse vibration control of an axially moving string system by Lyapunov method[J]. Control Theory & Applications, 2006, 23(4): 531-535. (in Chinese)
[81] 李志军,张伟. 轴向运动弦线横向振动状态反馈的H_∞控制[J]. 机械设计与制造工程, 2015, 44(1): 57-61.
Li Zhijun, Zhang Wei. Transverse vibration control of an axially moving string system on the state feedback control[J]. Machine Design and Manufacturing Engineering, 2015, 44(1): 57-61. (in Chinese)
[82] 刘定强,王忠民. 轴向运动矩形薄膜的横向振动控制[J]. 西安理工大学学报, 2007, 23(1): 62-65.
Liu Dingqiang, Wang Zhongmin. The transverse vibration control of an axially moving rectangular membrane[J]. Journal of Xi' an University of Technology, 2007, 23(1): 62-65. (in Chinese)
[83] 武吉梅,景涛,王砚,等. 计及弯曲刚度的印刷运动薄膜横向振动控制研究[J]. 应用数学和力学, 2015, 36(7): 686-699.
Wu Jimei, Jing Tao, Wang Yan, et al. Transverse vibration control of moving printing membranes with bending stiffness[J]. Applied Mathematics and Mechanics, 2015, 36(7): 686-699. (in Chinese)
[84] Nguyen Q C, Hong K S. Transverse vibration control of axially moving membranes by regulation of axial velocity[J]. IEEE Transactions on Control Systems Technology, 2012, 20(4): 1124-1131.
[85] Nguyen Q C, Hong K S. Stabilization of an axially moving web via regulation of axial velocity[J]. Journal of Sound and Vibration, 2011, 330(20): 4676-4688.
[86] Huang Yongan, Chen Jiankui, Yin Zhouping, et al. Roll-to-roll processing of flexible heterogeneous electronics with low interfacial residual stress[J]. IEEE Transactions on Components Packaging and Manufacturing Technology, 2011, 1(9): 1368-1377.
[87] 尹周平,陶波. 智能制造与RFID技术[J]. 航空制造技术, 2014(3): 32-35.
Yin Zhouping, Tao Bo. Intelligent manufacturing and RFID technology[J]. Aeronautical Manufacturing Technology, 2014(3): 32-35. (in Chinese)
[88] Chen Jiankui, Yin Zhouping, Xiong Youlun, et al. A hybrid control method of tension and position for a discontinuous web transport system[C]∥International Conference on Information and Automation. [S.l.]: IEEE, 2009: 265-270.
[89] 陈建魁. 非连续卷绕系统动力学建模与张力/位置控制及其应用[D]. 武汉: 华中科技大学, 2010.
[90] 陈建魁,丁汉,尹周平,等. 柔性卷绕传动张力控制机构分析与设计[J]. 现代制造工程, 2006(3): 1-3.
Chen Jiankui, Ding Han, Yin Zhouping, et al. Analysis and design of tension control structure in flexibly winding drive[J]. Modern Manufacturing Engineering, 2006(3): 1-3. (in Chinese)
[91] 周春雷. 柔性膜非连续放卷系统张力控制建模、仿真及实验[D]. 武汉: 华中科技大学, 2013.
[92] 邵琳. 柔性薄膜卷绕输送系统中张力控制研究与应用[D]. 武汉: 华中科技大学, 2012.
[93] 张锐. 柔性基板横向偏移量控制方法研究[D]. 武汉: 华中科技大学, 2012.
[94] Jain K, Klosner M, Zemel M, et al. Flexible electronics and displays: high-resolution, roll-to-roll, projection lithography and photoablation processing technologies for high-throughput production[J]. Proceedings of the IEEE, 2005, 93(8): 1500-1510.
[95] Lo C Y, Hiitola-Keinänen J, Huttunen O H, et al. Novel roll-to-roll lift-off patterned active-matrix display on flexible polymer substrate[J]. Microelectronic Engineering, 2009, 86(4-6): 979-983.
国家自然科学基金资助项目(51475195,51322507);国家科技支撑计划资助项目(2015BAF11B02)
2017-02-20;
2017-03-20
TH113

尹周平,男,1972年9月生,博士、教授、博士生导师。国家杰出青年基金获得者、教育部长江学者特聘教授。发表SCI论文100余篇,出版著作2部,授权发明专利80余项,获国家自然科学二等奖、国家技术发明二等奖、国家科技进步二等奖各1项。主要研究方向为电子制造技术与装备、数字化智能制造技术。
E-mail:yinzhp@hust.edu.cn

