传感器支架振动对扭振测量的影响及消除方法

王媛文， 董大伟， 孙梅云， 闫 兵

(1.西南交通大学机械工程学院 成都，610031) (2.中国北车集团唐山轨道客车有限责任公司 唐山，063035)

10.16450/j.cnki.issn.1004-6801.2017.05.003

传感器支架振动对扭振测量的影响及消除方法

王媛文1， 董大伟1， 孙梅云3， 闫 兵1

(1.西南交通大学机械工程学院 成都，610031) (2.中国北车集团唐山轨道客车有限责任公司 唐山，063035)

通过实验研究确定了传感器支架振动对扭振测量有较大影响，且由整机振动引起。从磁电传感器电压特性出发，以传感器支架振动影响下的传感器输出电压和瞬时转速表达式为基础，阐明了作用机理；同时研究了支架振动引起伪扭振信号的规律及频谱特征。研究表明，支架振动引起的伪扭振信号随着支架振动幅值的增加而增加；伪扭振信号的主要成分是支架振动的阶数及其二阶；所取基准电压越接近0，伪扭振信号幅值越小。提出了一种基于最佳基准电压的去除支架振动影响的新方法，并提出了最佳基准电压的计算方法。仿真研究表明，该方法是有效的，为改善扭振测量精度提供了理论依据，具有工程应用价值。

内燃机； 支架振动； 扭振测量误差； 最佳基准电压

引 言

多缸内燃机的扭振信号中，蕴含着丰富的内燃机(运行信息，是较好的故障诊断信号源[1-2]。较大的扭振易引起轴系零部件故障和车辆问题[3-5]。扭振测量准确与否，直接影响着故障诊断精度和整车NVH性能的改善效果，因此其测试误差影响规律和消除方法的讨论尤为重要。

目前工程中大多使用磁电传感器——齿盘法进行扭振信号测量。但是使用该方法过程中存在众多影响测试误差的因素，如轮盘偏心误差、传感器振动、轴心轨迹、齿形分度误差以及测量过程中的计数量化误差和触发误差等[6]。已有学者对扭振测量误差进行了一些研究。孙云岭等[6-8]对轴心轨迹和计数量化误差因素进行分析，将其影响分为调频、调幅和附加波形三类，提出在瞬时转速计算时，使用插值算法来减少其误差。到目前为止，还未见传感器支架振动影响下扭振测量误差的相关研究。

笔者首先通过实验研究确定了传感器支架振动对扭振信号测量影响的存在；然后，基于传感器支架振动影响下的扭振信号表达式，对其影响规律进行讨论；最后，提出一种基于最佳基准电压消除支架振动影响的新方法，同时提出了最佳基准电压的获取方法，并进行了仿真研究，证明该方法的有效性。

1 支架振动实验

转速测量过程中，磁电传感器安装于机体上，难免会产生传感器支架振动。为了确定传感器支架振动的存在，用如图1所示实验装置对2 011 r/min情况下的支架振动进行测量，测试对象为4100QB柴油机。图2和图3分别为支架和机体振动位移时域和频域曲线。从图中可以看出，支架和机体振动幅值最大的频率成分都是发动机的2阶，所以支架振动应为机体的整机振动引起。为了进一步确认支架振动的产生原因，对支架进行了敲击实验，图4所示为敲击实验得到的频谱图。从图中可以看出，支架的固有频率较高，最低阶固有频率202.4 Hz已经远远大于发动机正常工作转速范围内2阶激振力的频率。因此，可以判断扭振测量过程中存在支架振动，且支架振动的主要成分由整机振动激励下的强迫振动引起。

图1 支架振动研究实验台Fig.1 Testbed for studying sensor bracket vibration

图2 传感器支架和机体振动位移时域曲线Fig.2 Vibration displacement of sensor bracket and body

图3 传感器支架和机体振动位移频域曲线Fig.3 Vibration displacement spectrum of sensor bracket and body

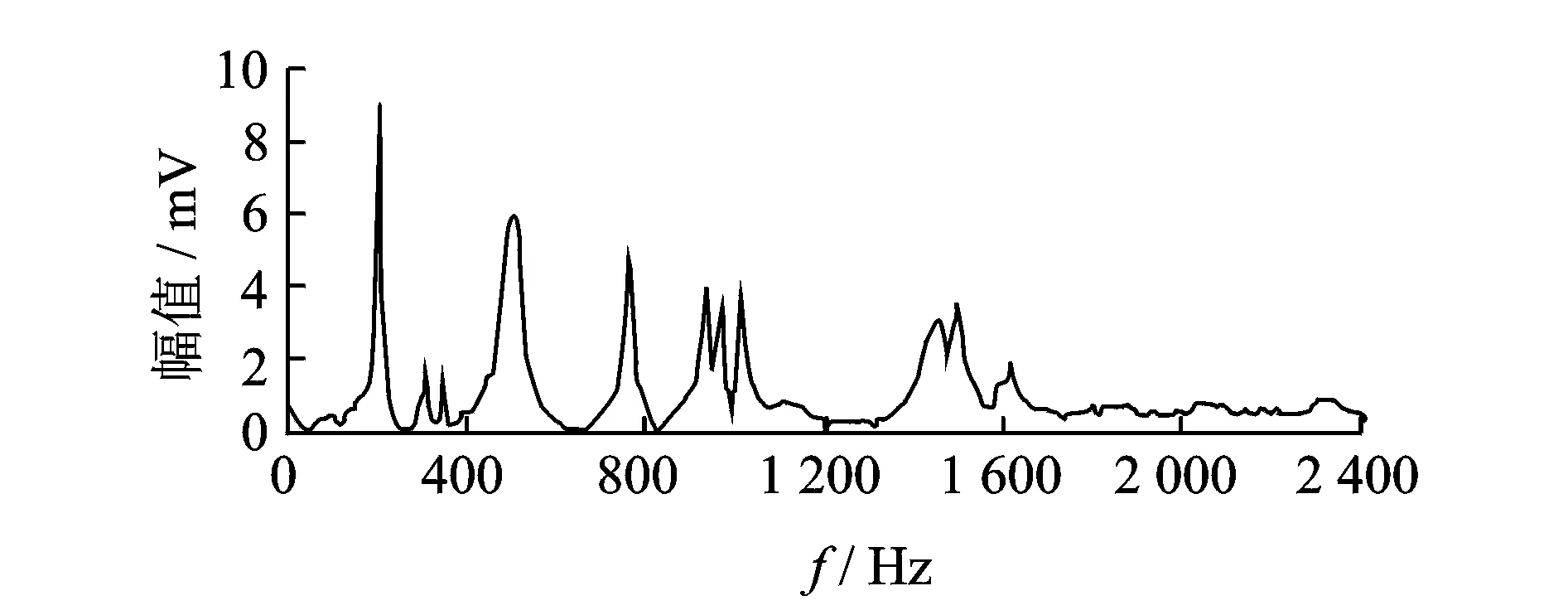
图4 传感器支架敲击实验频谱Fig.4 Frequency response curve of sensor bracket vibration, obtained by impact experiment

2 支架振动影响下的瞬时转速表达式

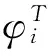
图5 支架振动原理图Fig.5 Mechanism of bracket vibration

经推导(详细推导过程及变量说明见文献[9])，存在支架振动情况下，从第i-1个齿顶到第i-1个齿底过程中，传感器输出电压信号表达式εsv如式(1)所示，第i个齿对应的瞬时转速ni如式(2)所示。

(1)

其中

Msv=

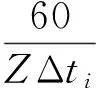
(2)

其中：K=NFS为传感器相关参数，传感器选定后为常数，N为线圈匝数，F为永久磁铁的磁动势，S为磁路截面积(m2)；μ0=4π×10-7H/m为真空磁导率；M=Zh/(δ2+δh)为齿盘及安装参数；ε0为基准电压。

3 传感器支架振动的影响规律

取空气磁导率μ0=4π×10-7H/m，齿盘半径R=61 mm，齿数Z=120，齿高h=5 mm，安装间隙δ=0.7 mm，转速n=1 200 r/min。支架振动幅值、支架振动阶数和基准电压3个变量分别取δa=0.1 mm，p=2和ε0=2 000 mV，在此基础上每次变化上述3个变量中的一个，其变化范围分别为：δa∈0～0.1 mm，步长0.001 mm；p∈1～10阶，步长1阶；ε0∈-4 000～4 000 mV，步长为100 mV。计算得到各个变量对瞬时转速测量的影响规律(伪扭振信号变化规律)，如图6(a)～(c)所示。图7为支架振动阶次p=2时的伪扭振信号时域和频域数据。从图6(a)中可以看出，支架振动幅值为0时，测量得到的转速为1 200 r/min，误差为0，符合客观认知；随着支架振动幅值的增大，瞬时转速测量误差不断增大。从图6(b)和图7中可以看出，p阶支架振动引起的伪扭振信号最主要的成分是p阶，2p阶也有较大幅值。从图6(c)可以看出，随着基准电压远离零基准电压，转速测量误差变大，当基准电压为0时，转速测量误差为0。从公式也可以看出，当基准电压ε0取0时，转速n的瞬时转速信号仍然为n，不存在误差。这为去除支架振动影响提供了一种新方法，即选取合适的最佳基准电压进行瞬时转速计算。

图6 各影响因素对伪扭振信号的影响规律曲线Fig.6 Curves of pseudo torsional vibration signal influenced by factors

图7 支架振动阶次p=2时计算得到的瞬时转速信号Fig.7 Transient speed signal calculated when bracket vibration order is p=2

4 支架振动影响的消除

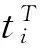
(3)

其中：n0，n1和n2分别为原始转速信号的均值、频率为ω1和频率为ω2部分的幅值。

(4)

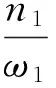
根据上述原理，仿真研究了不同基准电压对扭振测量的影响。仿真计算中，支架振动的主要成分为2阶，幅值δa=0.1 mm；扭振的主要成分为1阶和2阶，幅值分别为n1=2 mm，n2=2 mm。图8为原始扭振信号的时域和频域数据。图9为不同基准电压下扭振信号的频率成分。从中可以看出，随着基准电压靠近0基准电压，扭振信号第2，4阶明显减小，即在0基准电压附近有最小值点；而第1阶基本不变。结合上述规律研究结果，2阶支架振动引起的伪扭振信号主要是2阶和4阶，所以2阶和4阶明显减小。即基准电压靠近0时，明显减小的部分主要由支架振动引起，而未发生变化的部分是原有的扭振信号。

图8 原始扭振信号时域和频域曲线Fig.8 Time and frequency domain curve of original torsional vibration

图9 不同基准电压下扭振频域数据Fig.9 Frequency domain data calculated at different reference voltages

由上述性质得出以下消除支架振动影响的方法。在对实测信号处理时，以电压信号的平均值εa为初始值，在其δε邻域范围(εa-δε，εa+δε)内，寻找一个最佳基准电压εb，使得支架振动引起的阶次的幅值达到最小值。具体步骤如下：

1) 截取一个工作循环的电压信号ε(t)(或者多循环平均后的电压信号)。

2) 计算得到电压信号ε(t)的平均值εa，并选取一个邻域(εa-δε，εa+δε)，δε可选取电压信号最大值和平均值之差的一半。选取基准电压的变化增量Δε。用上述实验方法获得支架振动的主要阶次为p阶。

3) 以εa为初值，Δε为增量，分别计算得到各基准电压下扭振信号的p阶幅值，并求得p阶幅值最小值对应的基准电压，即最佳基准电压εb。

4) 按最佳基准电压εb计算得到扭振信号。

为了验证上述消除支架振动影响和最佳基准电压选取的方法是否有效，选取εa=100 mV，δε=4 000 mV，Δε=100 mV，对上述2阶支架振动影响下的以1阶和2阶为主要成分的扭振信号进行仿真计算，得到最佳基准电压εb=-100 mV。图10为基准电压分别取4 000 mV和-100 mV时扭振信号仿真结果与原始扭振信号的时域和频域曲线对比。从图中可以看出，当基准电压取4 000 mV时，在2阶和4阶产生较大的伪扭振信号，而1阶与原始扭振信号相同，在1阶未产生伪扭振信号，这与上述规律研究的结论相吻合。当基准电压取最佳基准电压εb=-100 mV时，时域曲线与原始扭振信号几乎重合，2阶支架振动引起的2阶和4阶伪扭振信号大幅下降，1阶和2阶的幅值与原始扭振信号的1阶和2阶幅值相同。也就是说，最佳基准电压几乎完全消除了支架振动引起的伪扭振信号， 同时完全保留了原始扭振信号。综上所述，通过在计算瞬时转速过程中选择最佳基准电压的方法可以有效地消除支架振动产生的影响，同时所提出的选择最佳基准电压的方法也是有效的。

图10 基准电压分别取4 000 mV和-100 mV时扭振信号仿真结果与原始扭振信号的时域和频域曲线对比Fig.10 Simulation results of torsional vibration calculated at different reference voltage

为了进一步验证该方法的有效性，对实验数据使用该方法，计算得到最佳基准电压65 mV，其对应的修正后扭振信号与原始扭振信号频谱图对比如图11所示。由图可知，2阶和4阶有明显减小，其中2阶最为明显。由于支架振动的主要阶次依次是2阶和4阶，根据上文特性可知，由支架振动引起的伪扭振信号主要阶次也是2阶和4阶，因此，最优基准电压有效地消除了支架振动引起的伪扭振信号。2阶和4阶剩余的部分则为除支架振动影响后的扭振信号。

图11 最优基准电压时扭振信号与原始扭振信号频谱图Fig.11 Frequency curves of torsional vibration signal calculated at optimal and original reference voltage

5 结 论

1) 通过实验研究，证明了传感器支架振动确实存在；传感器支架振动由整机振动引起，并非其自身共振。

2) 研究了支架振动对扭振测量的影响规律。随着支架振动幅值的增大，瞬时转速测量误差不断增大；p阶支架振动引起的伪扭振信号最主要的成分是p阶，2p阶也有较大幅值；随着基准电压远离零基准电压，转速测量误差变大。

3) 提出了一种基于最佳基准电压的消除支架振动影响的新方法，同时提出了最佳基准电压的获取方法，并进行了仿真和实验研究，证明该方法能够有效消除传感器支架振动的影响，获得最佳基准电压的方法也是有效的。

[1] Franco J, Franchek M A, Grigoriadis K. Real-time brake torque estimation for internal combustion engines[J]. Mechanical Systems and Signal Processing, 2008,22(2):338-361.

[2] Gawande S H, Navale L G, Nandgaonkar M R. Power balancing of inline multicylinder diesel engine[J]. Advances in Mechanical Engineering, 2012(2012):9.

[3] 周迅，俞小莉，李松和.扭振测量误差分析及实用发动机高精度扭振测量仪的研制[J].内燃机工程,2005,26(5):77-80.

Zhou Xun, Yu Xiaoli, Li Songhe. Investigation of torsional vibration measurement and development of a new digital torsional vibration instrument with high precision for engine[J]. Chinese Internal Combustion Engine Engineering, 2005,26(5):77-80. (in Chinese)

[4] 蒋云帆，廖明夫，王四季.航空发动机转子扭振测量新方法[J].振动、测试与诊断,2013,33(3):410-415.

Jiang Yunfan, Liao Mingfu, Wang Siji. New measuring method for torsional vibration of aeroengine rotor[J]. Journal of Vibration, Measurement & Diagnosis, 2013,33(3):410-415. (in Chinese)

[5] 上官文斌，陈超，段小成，等.发动机曲轴系统扭转振动建模与实测分析[J].振动、测试与诊断,2012,32(4):560-567.

Shangguan Wenbin, Chen Chao, Duan Xiaocheng, et al. Modeling and experiment analysis of torsional vibration in engine crankshaft system[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(4):560-567. (in Chinese)

[6] 张永祥，孙云岭，李军，等.柴油机瞬时转速测量中误差处理技术研究[J].内燃机工程,2005,26(6):61-63.

Zhang Yongxiang, Sun Yunling, Li Jun, et al. Research on transient rotating speed measurement errors process technology for diesel engines[J]. Chinese Internal Combustion Engine Engineering, 2005,26(6):61-63. (in Chinese)

[7] 孙云岭，朴甲哲，张永祥，等.内燃机瞬时转速测量干扰因素分类与仿真[J].海军工程大学学报，2003,15(4):81-85.

Sun Yunling, Piao Jiazhe, Zhang Yongxiang, et al. Classification and simulation of interference factors in the measurement of ICE transient speed[J]. Journal of Naval University of Engineering, 2003,15(4):81-85. (in Chinese)

[8] 孙云岭，朴甲哲，张永祥.插值算法在内燃机瞬时转速测量中的应用研究[J].内燃机学报,2002,20(4):335-338.

Sun Yunling, Piao Jiazhe, Zhang Yongxiang. Investigation on interpolation method in transient speed measurement for internal combustion engines[J]. Transactions of CSICE, 2002,20(4):335-338. (in Chinese)

[9] 王媛文，董大伟，闫兵.传感器工作间隙对内燃机瞬时转速测量的影响机理及规律[J].内燃机学报,2014,32(5):466-473.

Wang Yuanwen, Dong Dawei, Yan Bing. Influence mechanism and law of sensor working clearance on instantaneous engine speed measurements[J]. Transactions of CSICE, 2014,32(5):466-473. (in Chinese)

国家自然科学基金资助项目(51275426)

2015-06-23；

2015-08-30

TK411+.6; TK417+.127; TH133.5

王媛文，男，1984年5月生，博士生。主要研究方向为汽车动力传动系扭振控制。曾发表《传感器工作间隙对内燃机瞬时转速测量的影响机理及规律》(《内燃机学报》2014年第32卷第5期)等论文。

E-mail：wywqsr1984517@163.com

闫兵，男，1964年11月生，博士、教授。主要研究方向为机械设备振动计算、测试、控制及故障诊断。

E-mail：yanbingwd@163.com