基于HSGT的装备健康状态评估技术
谭晓栋, 邱 静, 罗建禄, 李 庆, 吕克洪
(1.电子科技大学机械电子工程学院 成都,610054)(2.国防科学技术大学装备综合保障国防科技重点实验室 长沙,410073)(3.武警警官学院电子技术系 成都,610213)
10.16450/j.cnki.issn.1004-6801.2017.05.005
基于HSGT的装备健康状态评估技术
谭晓栋1, 邱 静3, 罗建禄3, 李 庆3, 吕克洪3
(1.电子科技大学机械电子工程学院 成都,610054)(2.国防科学技术大学装备综合保障国防科技重点实验室 长沙,410073)(3.武警警官学院电子技术系 成都,610213)
提出了基于健康状态-广义测试相关性(health state-general test, 简称HSGT)的健康状态评估技术。首先,根据维修要求将故障严重程度划分成多个离散的健康状态,再按测试输出属性,将测试划分为一系列区间值的广义测试,进而结合系统功能与结构等信息,建立系统健康状态-广义测试相关性矩阵;其次,利用贝叶斯理论,建立基于HSGT的健康状态评估推理模型;最后,使用蒙特卡洛方法生成包含8个被测单元(unit under test, 简称UUT)的系统,对所提技术的有效性及可行性进行了仿真验证。结果表明,提出的健康状态评估技术能根据系统测试输出结果,及时、准确地推理出系统中各个UUT的健康状态,评估结果能在故障加剧导致的功能失效前有效触发视情维修(condition based maintenance,简称CBM)的维修决策机制。
健康状态评估; 状态基维修; 健康状态-广义测试相关性; 被测单元
引 言
高新技术装备复杂度及集成度的急剧增加给装备的测试维修带来了极大的挑战。为减少装备的维修费用,提高装备的可用性和战斗力,装备的维修保障模式已由传统的事后维修、定期维修向视情维修转变。健康状态评估(health state assessment, 简称HSA)作为这些新型保障体系中的关键技术,能有效触发CBM的维修决策机制,是实现CBM的前提和基础[1-2]。
健康状态评估扩展了故障诊断的功能,考虑融合各种数据信息,通过智能推理辨识当前故障严重程度(损伤度)或者被测单元的健康状态(性能退化情况)。在当前健康状态的评估结果基础上实现剩余寿命估计、故障预测和告警,进而在故障导致UUT功能失效前采取主动的维修策略防止故障加剧或系统性能的进一步恶化,对于降低系统运行费用、避免关键任务的中断和灾难性事故的发生具有重要意义[3-4]。
健康状态评估方法主要分为两类:基于数据驱动及基于物理模型的方法[5-6]。基于数据驱动的方法是从时域、频域、时频域提取测量信号的故障特征,与正常状态下的特征进行比较,进而评估出退化程度。Niu等[7]利用Mahalanobis距离和Weibull分布作为健康决策指标,实现了电子产品健康评估。Mihai等[8]利用二阶抛物回归的方法评估和预测镍氢电池的状态。李俨等[9]提出了基于层次分析法和三角模糊数相结合的无人机健康状态评估方法。李丽敏等[10]根据航空发动机突发故障的历史监测数据建立MOG-HMM模型,确定故障的状态数,进而为故障预测提供数据支撑。然而,基于数据的健康状态评估方法大多针对单一的部件或系统,不能辅助CBM的系统维修。
基于物理模型的HSA方法是使用一个部件或者子系统的物理模型,通过比较测量信号与模型输出值的残差或趋势评估系统的退化程度,该方法逻辑推理严密,在材料、机械和电子产品等领域的损伤检测和预测中得到了广泛应用[11]。在材料和机械领域中,一般将关键部件损伤表征为健康状态的函数,并以疲劳累积损伤方法评估健康状态。Kacprzrnski等[12]通过融合失效物理模型与相关诊断信息,对直升机齿轮箱进行了状态评估。Peter等[13]使用开关卡尔曼滤波(switching Kalman filters, 简称SKF)方法指导直升机齿轮箱轴承的故障检测和剩余寿命估计,该方法利用多个动态模型描述轴承不同性能退化过程。由于复杂系统精确的物理模型建模成本高、精度低,制约了基于模型的HSA的准确性。
综上所述,在目前基于数据或物理模型的健康状态评估方法中,由于数据驱动的方法需要大量的试验和历史数据,没有有效的利用装备的功能、结构等设计信息,在工程中应用效果有限。对于复杂系统而言,由于物理模型很难精确建立以及不确定等问题,导致基于物理模型的健康状态评估准确度较低。综合二者优缺点,受到基于故障-测试相关性模型进行诊断推理取得成功的启发,笔者结合系统的功能结构信息、测试输出信息、部件性能退化特征等信息,建立描述UUT健康状态(性能退化状态)对系统测试参数影响关系的健康状态-广义测试相关性矩阵,在此基础上,使用贝叶斯动态推理理论,提出基于健康状态-广义测试相关性的健康状态评估方法。该方法有效融合了装备功能结构信息、测试输出信息以及UUT性能退化特性等多方数据信息,有望提高健康状态评估效率和评估精度。同时,评估出系统中所有UUT的健康状态结论能为CBM的系统级以及基层级的维修决策提供有效的数据支撑。
1 健康状态与广义测试相关性
对系统中的UUT而言,从正常状态到故障早期状态,直至功能失效状态会经历一个性能逐渐退化的过程。对故障模式而言,则会经历一个故障严重程度逐渐加剧的故障演化过程,如齿轮裂纹故障会经历从轻微裂纹程度到裂纹加剧直至由于裂纹导致轮齿折断这样一个裂纹演化过程。此时,把健康状态定义为一系列表征UUT性能退化或故障演化过程中不同故障严重程度(或损伤度)的离散状态。同时,对不同健康状态下所表现出来的征兆特征,采用相应的测试节点进行观测。这些测试观测值的区间也对应着不同健康状态。基于此,笔者使用健康状态-广义测试矩阵描述系统中各个UUT的健康状态与广义测试的相关性关系。
gt11gt12…gtl
(1)
其中:xij表示为第i个UUT对应的第j个健康状态,当其出现时xij=1,否则,xij=0。gtl表示为第l个测试tl的第个广义测试。矩阵中元素dijl表示第i个UUT处于第j个健康状态时(即xij=1),测试tl的第个广义测试gtl对能否对xij进行有效评估。如果能,则dijl=1;否则dijl=0。
值得注意的是,与传统的故障-测试矩阵(fault-test,简称FT)不同点在于:文中把系统中的UUT分成了多个表征不同损伤程度的健康状态,如正常状态、健康状态1,…,到失效状态。同时,根据测试输出属性,把测试划分为一系列区间值的广义测试(general test,简称GT)。
2 HSA 问题的数学推导
HSA问题的实质就是根据当前时刻系统中测试的输出结果,结合健康状态-测试相关性矩阵和先验概率等信息,评估出系统中UUT最有可能的健康状态,使评估结果与真实状态相一致。
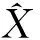
(2)
其中:X={x11,…,x1L1,…,xi1,…,xiLi,…}为系统中M个UUT对应的健康状态集;ψGTP,ψGTF分别表示广义测试集ψGT中“通过”及“不通过”的广义测试集;S为系统中所有可能的健康状态集。
由于各个测试数据间相互独立,因此式(2)等价为下式
(3)
其中:P(ψGTP|X),P(ψGTF|X)分别为在健康状态集X下,广义测试 “通过”和“不通过”的概率,P(X)为系统中所有UUT健康状态的先验概率,可以通过下式表示
(4)
其中:xij为系统中第i个UUT的第j个健康状态;Li为第i个UUT健康状态总数;M为系统中UUT的总数;p(xij)为健康状态xij发生的先验概率。
假定理想状态下,各个广义测试互不干扰,则对给定健康状态集X,系统广义测试输出结果“通过”的概率P(ψGTP|X)和“不通过”的概率P(ψGTF|X)可用下式表示
(5)
(6)
其中:gtl表示第l个测试tl的第个广义测试。
健康状态-广义测试的关系如图1所示,xij=0表示健康状态xij不出现,xij=1表示健康状态xij出现。ol表示广义测试gtl的输出值,当gtl能评估出某个健康状态时,ol=1;否则ol=0。Pdijl表示健康状态xij=1,广义测试gtl能对xij进行有效评估的概率;Pfijl表示健康状态xij不出现(即xij=0),广义测试gtl错误评估其出现的概率。

图1 健康状态与广义测试间的关系Fig.1 The relationships between health states and general tests
从图1中关系,可以得出如下结论
P(ol= 0|xij)=(1-Pdijl)xij·(1-Pfijl)(1-xij )
(7)
假定各个测试相对独立,有
P(tl∈ψGTP|
(1-Pfijl(1-xij)
(8)
P(tl∈ψGTF|X) = 1-P(tl∈ψGTP|X)
(9)
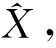
(10)

(11)


(12)
此外,式(11)中健康状态xij发生的先验概率态p(xij)、广义测试gtl错误评估概率Pfijl出现的概率可以通过专家经验获取(默认为常量)。同时,由于式(12)是求解以xij为自变量的函数最小值,因此,为了减少不必要的计算,可以在式(11)中直接去掉与自变量xij无关的常量项ln(1-p(xij)) 及ln(1-Pfijl)。
另外,为了对式(11)进行简化,定义新的变量yl为
(13)
根据以上化简和替换结果,式(12)的主函数问题等价为
(14)
其中:i=1,…,M;j=1,…,Li。
当考虑广义测试输出结果不确定性因素时,健康状态评估问题面临如下约束。
1) 新定义的变量
ln(yl)=
(15)
2) 在某一时刻系统中的第i个UUT必须也只能处于一个健康状态,即
(16)
笔者推导的HSA问题是一个具有两个约束的NP-难问题。利用文献[16-17]介绍的 LR-AGA方法对模型进行求解。将问题分解为两层优化问题:在顶层,使用遗传算法更新拉格朗日乘子来整体协调获得整个系统的可行解;在底层,使用遗传算法求解松弛后的对偶问题,即单个部件状态评估优化问题。在上级对拉格朗日乘子进行寻优,在下级对变量x进行寻优。两层的信息交互过程为:在上级,初始化拉格朗日乘子,使用自适应方法更新拉格朗日乘子,建立子种群,将个体传给下级;在下级,针对这些特定的λl(k)与μi(k)个体,求解出变量x的最优个体x*,将这些最优x*传回上级,计算每个λl(k)与μi(k)个体对应的适配值。上下两级同时采用遗传算法解决每个子问题,在给定拉格朗日乘子λl(k)与μi(k)情况下,获得每个UUT的优化状态序列[3]。
3 案例验证
使用一个仿真系统验证文中所提方法的有效性,该系统包括x1~x88个UUT,其相关性模型如图2所示。假定系统中x1,x2,x4,x74个UUT为突发功能失效部件,把这4个UUT的全寿命过程分为两个健康状态:正常状态和功能失效状态;假定x3,x5,x6,x8为性能缓变退化部件,把这些UUT的全寿命过程分为3个健康状态:正常状态、性能退化状态、完全失效状态。对于该仿真系统的8个UUT,可以获得总共20个健康状态X={x11,x12,x21,x22,x31,x32,x33,x41,x42,x51,x52,x53,x61,x62,x63,x71,x72,x81,x82,x83},例如,x11,x12分别对应部件x1的正常状态及功能失效状态,x31,x32,x33分别部件x3的正常状态、性能退化状态和完全失效状态。广义测试ψGT={gt11,gt12,gt21,gt22,gt23,gt31,gt32,gt41,gt42,gt43,gt51,gt52,gt61,gt62,gt63,gt71,gt72,gt81,gt82,gt83},例如,gt11,gt12分别表示测试t1对应的两个广义测试,其他类似。采用文献[3]提出的方法建立该仿真系统的健康状态与广义测试的相关性矩阵[3],详细信息如表1所示。
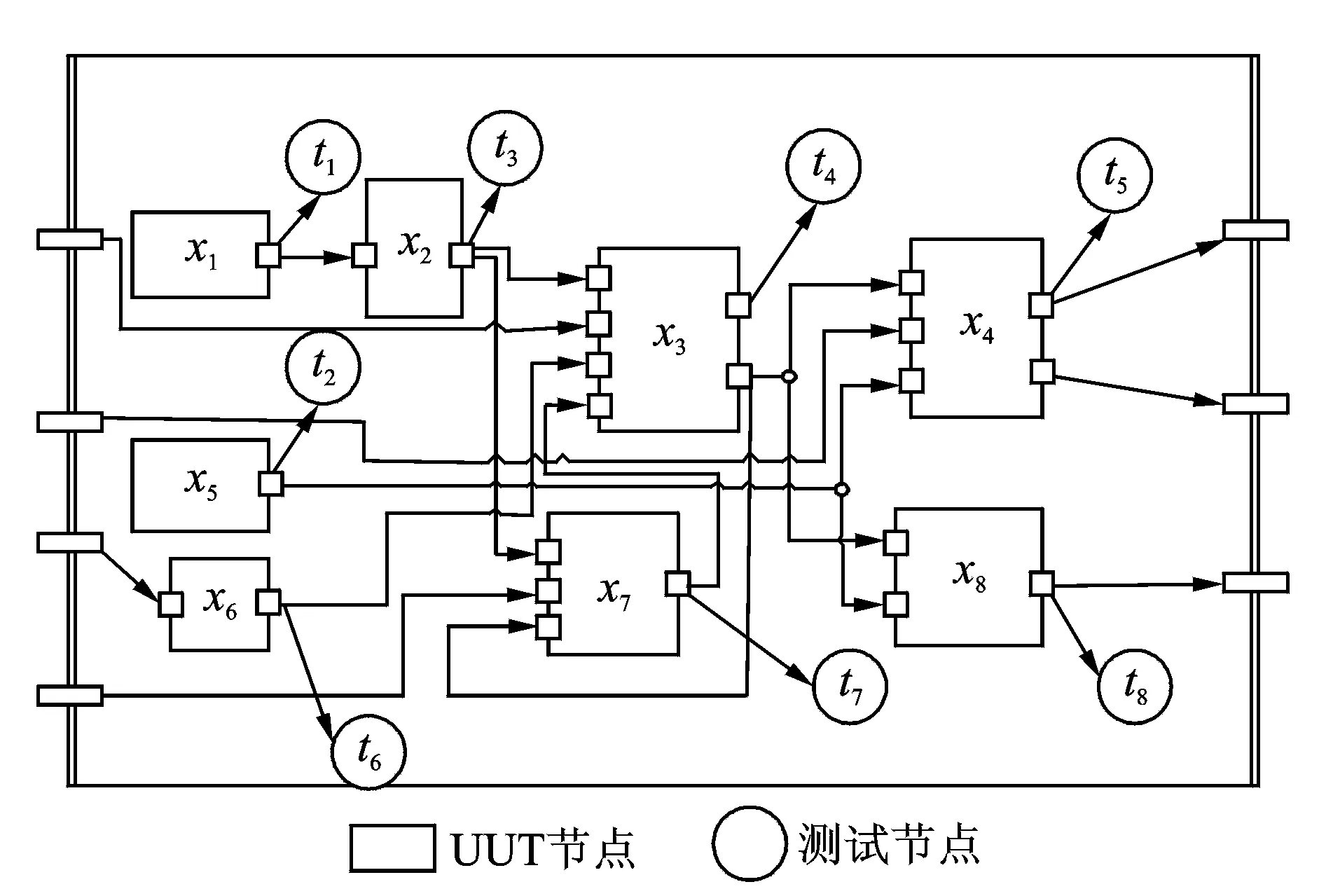
图2 仿真系统的相关性模型Fig.2 The dependency model of a simulation system
Tab.1Thedependencymatrixbetweenhealth-statesandgeneraltests

Xt1t2…t4gt11gt12gt21gt22gt23…gt42gt43x1x1110000…00x1201000…01x2x2100000…00x2200000…01x3x3100000…00x3200000…10x3300000…01x4x4100000…00x4200000…00x5x510010…000x520001…000x530000…000x6x610000…100x620000…000x630000…001x7x710000…000x720000…000x8x810000…000x820000…000x830000…000
此外,对健康状态评估模型中的正确评估概率Pdijl和错误评估概率Pfijl作出以下假设:广义测试对健康状态的正确评估概率Pdijl介于0.5~1.0间,错误评估概率Pfijl介于0~0.06之间,测试覆盖了系统中所有UUT的健康状态。为了验证健康状态评估结果的准确性,采用蒙特卡洛仿真方法,模拟产生10个时刻的广义测试输出结果。如k=1时刻,“通过”的广义测试ψGTP(1)={gt12,gt21,gt32,gt33,gt42,gt51,gt62,gt63,gt72,gt73,gt82,gt83,},“不通过”的广义测试集ψGTF(1)={gt11,gt22,gt31,gt41,gt52,gt61,gt71,gt81}。

使用LRAGA方法对HSA模型进行求解,求解算法中的参数设置如下:种群数为40,交叉概率为0.9,变异概率为0.01,得到如图3所示的对偶间隙收敛曲线。从图中可以看出,随着迭代次数的增加,对偶间隙逐渐降低,经过225次迭代后,计算时间为0.39 s,对偶间隙收敛到5.36%。

图3 对偶间隙收敛曲线Fig.3 The convergence curves of duality gap
表2列出了k=0~9时刻健康状态评估结论,如k=1时,评估结果为{1,0,1,0,1,0,0,1,0, 1,0,0,1,0,0,1,0,1,0,0},表明系统中8个UUT都处于正常状态,而系统的真实状态为{1,0,1,0,1,0,0,1,0,1,0,0,1,0,0,0,1,1,0,0},即被测单元x1,x2,x3,x4,x5,x6,x8处于正常状态,而x7处于失效状态,健康状态评估准确率为95%。统计计算出10个时刻平均健康状态评估准确率96.5%。试验结果表明,该算法能很好的解决健康状态评估问题,能实现较好的健康状态评估性能。

表2 10个时刻的测点输出及评估结果
4 结束语
通过考虑系统结构、功能特点及状态维修需求,笔者提出了基于健康状态-广义测试相关性的健康状态评估的技术。基于HSGT的健康状态评估模型准确地描述系统中性能退化UUT相互间关系以及对系统参数的影响关系。仿真试验结果表明,基于LRAGA的HSA模型求解方法能根据系统测试参数的输出结果准确评估出各个UUT的性能退化状态。针对评估结论中性能退化的UUT可提前采取维修决策,避免系统中UUT突发功能失效造成的损失,对于减少系统的维修费用、提高系统的可用度具有重要的意义。此外,笔者所建立的HSA模型同样也适用于那些故障演化过程具有缓变特性的故障模式,可用于建立故障间的传播关系、不同故障严重程度对测试参数的影响,根据这些关系可在故障程度逐渐加剧导致的突发失效前评估故障的严重程度,避免故障程度的加大。该技术成果将应用到功能结构复杂的真实系统中。
[1] Caballéa N C, Castroa I T, Pérezb C J. A condition-based maintenance of a dependent degradation-threshold-shock model in a system with multiple degradation processes[J]. Reliability Engineering and System Safety, 2015,134:98-109.
[2] Zhang Tieling, Richard D, Khaled E. Condition based maintenance and operation of wind turbines[C]∥Proceedings of the 8th World Congress on Engineering Asset Management. Berlin: Springer International Publishing, 2015:1013-1025.
[3] 谭晓栋.面向健康状态评估的可测性关键技术研究[D].长沙:国防科学技术大学, 2013.
[4] 张金春,张继军,曹彪.基于HMM的机载设备状态健康评估方法研究[J].计算机测量与控制,2015,23(2):491-493.
Zhang Jinchun, Zhang Jijun, Cao Biao. Research on state health evaluation method of airborne equipments based on HMM[J]. Computer Measurement & Control, 2015,23(2):491-493. (in Chinese)
[5] David S. Evaluation of health assessment techniques for rotating machinery[D]. Cincinnati: University of Cincinnati, 2009.
[6] Manzar A. System level health assessment of complex engineered processes[D]. Atlanta: Georgia Institute of Technology, 2010.
[7] Niu G, Singh S, Holland S W. Mahalanobis distance and projection pursuit analysis for health assessment of electronic systems[J]. Microelectronics Reliability, 2007,51(2):279-284.
[8] Mihai V M, Lucian U, Gabriel N, et al. Online state-of-health assessment for battery management systems[J]. IEEE Transaction on Instrumentation and Measurement, 2011,60(6):1997-2005.
[9] 李俨,陈海,张清江,等.无人机系统健康状态评估方法研究[J].系统工程与电子技术,2011,33(3):562-567.
Li Yan, Chen Hai, Zhang Qingjiang, et al. Assessment method of health condition for UAV systems[J]. Journal of Systems Engineering and Electronics, 2011,33(3):562-567. (in Chinese)
[10] 李丽敏,王仲生,姜洪开.基于MOG-HMM和Viterbi的航空发动机突发故障预测[J].振动、测试与诊断, 2014,34(2):310-314.
Li Limin, Wang Zhongsheng, Jiang Hongkai. Sudden fault prognosis for aero engines based on MOG-HMM and viterbi[J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(2):310-314. (in Chinese)
[11] Gu Jie, Lau D, Pecht M. Health assessment and prognostics of electronic products[C]∥8th International Conference on Reliability, Maintenance and Safety. Piscataway: IEEE Computer Society, 2009:912-919.
[12] Kacprzrnski G, Sadashliar A, Roemer L B. Calibration of failure mechanism-based prognosis with vibratory state awareness applied to the H-60 Gearbox[C]∥IEEE Aerospace Conference. Washington: IEEE Computer Society, 2003:1-10.
[13] Peter W T, Joseph M, Wong K, et al. Fault detection and remaining useful life estimation using switching kalman filters[C]∥Proceedings of the 8th World Congress on Engineering Asset Management. Berlin: Springer International Publishing, 2015:53-64.
[14] Ruan Sui, Zhou Yunkai, Yu Feili. Dynamic multi-fault diagnosis with imperfect tests[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2009,39(6):1224-1236.
[15] Singh S. Dynamic multiple fault diagnosis: mathematical formulations and solution techniques[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2009,39(1): 160-176.
[16] Ongsakul W, Petchaaraks N. Unit commitment by enhanced adaptive lagrangian relaxation[J]. IEEE Transactions on Power Systems, 2004,19(1):620-628.
[17] Ren Hui, Wei Dan, Watts David, et al. Adaptive genetic algorithm based parameters optimization of PI controller for battery system in wind farm[J]. Advanced Materials Research, 2014,1055(1):375-382.
国家自然科学基金资助项目(61403408)
2015-07-06;
2015-12-31
TH17

谭晓栋,男,1983年10月生,博士生、讲师。主要研究方向为装备状态监控与故障诊断、故障预测与健康管理、测试性设计等。曾发表《Health state evaluation for aerospace systems》(《Aircraft Engineering and Aerospace Technology》2013,Vol.85,No.2)等论文。
E-mail:xdt1010@126.com

