基于多尺度核独立成分分析的柴油机故障诊断
刘 敏, 李志宁, 张英堂, 范红波, 詹 超
(1.军械工程学院七系 石家庄,050003) (2.西安军事代表局驻803厂军事代表室 西安,710043)
10.16450/j.cnki.issn.1004-6801.2017.05.006
基于多尺度核独立成分分析的柴油机故障诊断
刘 敏1, 李志宁1, 张英堂1, 范红波1, 詹 超3
(1.军械工程学院七系 石家庄,050003) (2.西安军事代表局驻803厂军事代表室 西安,710043)
为提高利用缸盖振动信号进行柴油机故障诊断的精度和速度,提出了一种基于多尺度核独立成分分析提取故障敏感频带的柴油机故障诊断方法。首先,提出奇异值能量标准谱对缸盖振动信号中的微弱冲击特征进行增强;然后,对信号进行固有时间尺度分解,并基于相关性准则选择有效频带分量;最后,利用核独立成分分析消除有效频带之间的频带混叠,得到故障敏感信息集中的独立频带,并计算其自回归模型(auto regression model,简称AR)参数、模糊熵和标准化能量矩作为特征向量输入核极限学习机(kernel extreme learning machine,简称KELM)进行柴油机故障诊断。试验分析结果表明,该方法可以快速准确地提取缸盖振动信号中的柴油机故障敏感频带,增强故障敏感特征,故障诊断准确率达到99.65%。
奇异值能量标准谱; 固有时间尺度分解; 核独立成分分析; 故障敏感频带; 柴油机故障诊断
引 言
柴油机缸盖振动信号由缸内气体燃爆冲击、进排气门开启与落座冲击、活塞往复惯性冲击以及各种随机激励信号叠加耦合而成,含有丰富的柴油机状态信息。不同的激励源信号对柴油机的不同状态具有不同的敏感性[1],但是由于不同激励源信号相互混叠,相对微弱的故障敏感信息往往被非敏感信息所覆盖,增加了特征提取的难度。因此,在时频域上对不同振源信号进行分离是增强信号的局部特征,提高特征参数敏感性和辨识度的关键。
目前,双树复小波包[1]、经验模式分解[2](empirical mode decomposition,简称EMD)、主成分分析[3]等方法被广泛地应用于缸盖振动信号的多尺度分析。但以上方法均无法准确分离出故障敏感频带,导致柴油机故障诊断精度普遍不高。EMD和独立成分分析(independent component analysis,简称ICA)相结合的方法在信号分离与识别领域得到了广泛应用[4-5]。但是EMD存在较大端点效应、模态混叠和计算速度慢等缺点,而ICA对非线性信号处理能力差,不利于缸盖振动信号的时频分析[6]。Frei等[7]提出的固有时间尺度分解(intrinsic time-scale decomposition, 简称ITD)方法,与EMD等相比计算速度快,端点效应小,分解精度高[8]。与传统的ICA相比,核独立成分分析(kernel independent component analysis,简称KICA)具有更高的灵活性和鲁棒性[6,9]。因此,笔者提出了基于ITD和KICA的缸盖振动信号多尺度分析方法。首先提出奇异值能量标准谱(singular value energy standard spectrum,简称SVESS)增强信号中的微弱冲击特征,然后利用ITD将信号分解到不同频带,进而根据相关性准则选择有效频带进行KICA处理,得到消除频带混叠的独立分量,最后对各独立分量分别提取特征并输入到KELM中实现柴油机故障的分类与诊断。
1 奇异值能量标准谱
奇异值分解是去除非线性、非平稳信号中的噪声并增强信号固有特性的有力工具,其算法难点在于选择最佳信号重构阶数,笔者提出奇异值能量标准谱的方法选择信号重构阶数。奇异值能量标准谱定义为

(1)
将序列Si(i=1,2,…,r)称为奇异值能量标准谱。由于有用信号能量分布集中,对奇异值的贡献主要集中在σi,(i=1,2,…,s)上,能量值较大;噪声信号能量相对分散,能量值远远小于有用信号[10]。在奇异值能量标准谱上表现为:有用信号谱线幅值大而陡峭,噪声谱线幅值小而平缓。因此,奇异值能量标准谱线必然会出现明显的拐点,此点即为有用信号和噪声的分界点,而且此点必然是唯一确定的,从而解决了奇异值差分谱中出现多个较大峰值点时分界点难以确定的问题。
2 固有时间尺度分解
ITD可对任意复杂信号进行不同时间尺度的分解,得到若干个固有旋转分量(proper rotation component,简称PRC)和一个趋势分量,其计算过程如下。
设Xt为采样信号,{τk,k=1,2,…,n}为Xt的所有局部极值点所对应的时间序列,令τ0=0。设L为Xt的基线提取因子,一次ITD分解算式为
Ht=(1-L)Xt=Xt-Lt
(2)
其中:Lt=LXt为基线分量;Ht=(1-L)Xt为固有旋转分量。
令Xk和Lk分别表示X(τk)和L(τk)。设Lt和Ht的定义域为[0,τk],Xt的定义域为[0,τk+2],则在连续的极值点间隔[τk,τk+1]内可定义Xt的分段线性基线提取因子L
其中:α∈[0,1]表示线性缩放,用来控制各固有旋转分量的振幅,其值通常取为0.5。
重复以上过程,将原始信号分解成若干个固有旋转分量与一个单调趋势分量,各固有旋转分量按照频率从高到低一次排列。分解过程可以表示为
(5)
其中:HLkXt为第(k+1)层固有旋转分量;LpXt为单调趋势分量或最低频基线信号。
3 核独立成分分析
KICA利用再生核希尔伯特空间内的非线性函数作为对比函数,把信号映射到高维空间,并运用核分析方法在该空间内寻找对比函数的最小值,从而得到最优解混矩阵,将源信号从观测样本信号中分离提取出来。KICA的分析步骤如下:
1) 输入离散时间序列x1,x2,…,xn,并给定核函数k(x,s)对序列进行中心化和白化处理;
2) 利用Cholesky分解计算原始独立数据s1,s2,…,sn的Gram矩阵K1,K2,…,Km,其中si=Wxi,W为解混矩阵;
3) 定义λ(K1,K2,…,Km)为式(6)最大特征值
(6)

重复步骤2)和4),直到算法收敛使得C(W)取得最小值为止,从而求得最优解混矩阵W,进而根据s=Wx得到一组独立源信号。
根据以上分析可知,建立的柴油机故障诊断模型处理过程如图1所示。

图1 基于SVESS-ITD-KICA的柴油机故障诊断模型Fig.1 Diesel enginefault diagnosis model based on SVESS-ITD-KICA
4 柴油机缸盖振动信号测试与分析
4.1 信号测试试验
试验以F3L912型柴油机为研究对象,转速保持1 200r/min匀速空载运行。采集其第1缸缸盖振动信号,采样频率为40kHz。实验中设置了8种工况,分别为正常工况、进气门间隙过大、进气门间隙过小、排气门间隙过大、排气门间隙过小、进气门漏气、排气门漏气和1缸失火,气门故障均设置在1缸。对振动测试结果分析可知:此型柴油机缸盖振动信号的有效频带为1 000~7 000Hz[2],主要包括缸内气体燃爆冲击和进排气门开启与落座冲击,分别对应低频段和高频段。以1缸失火工况为例,缸盖振动信号的时域波形与时频谱如图2所示。由图可知:实测缸盖振动信号中含有大量分布于全频带的干扰噪声,微弱的冲击特征受到削弱甚至覆盖,不易提取故障特征。

图2 缸盖振动信号时域波形及其时频分布Fig.2 Time domain waveform and time-frequency distribution of the cylinder head vibration signal
4.2 缸盖振动信号特征增强
采用SVESS对缸盖振动信号进行冲击特征增强。以1缸失火工况下的缸盖振动信号为例,一个工作循环内的缸盖振动信号奇异值能量标准谱及特征增强前后的信号时域波形如图3所示。

图3 1缸失火Fig.3 First cylinder misfire
图3(a)中红框标注的奇异值即为有用信号和噪声的分界点,利用分界点及其之前的奇异值进行信号重构得到特征增强后的信号时域波形与功率谱如图3(b)~(e)所示。由图3可知:特征增强前的缸盖振动信号频带宽,能量分散,且冲击特征模糊,各工况下的信号特征辨识度差。经过特征增强之后,信号的能量主要集中分布在1 000~7 000 Hz之间,冲击特征得到有效增强,而且不同工况下的信号能量分布特征表现出明显的差别。
4.3 故障敏感频带分离
冲击特征增强后含有微弱故障信息的敏感频带仍然混叠于非敏感频带,因此实现各有效频带的分离是提取故障敏感信息的关键。对降噪后的缸盖振动信号进行ITD分解,并计算各PRC分量与原信号的互相关系数,选取互相关系数较大的前3个分量作为有效信源信号组成虚拟通道,并利用KCCA算法进行KICA处理,得到3个独立分量。其中,核函数选择高斯核函数。
缸盖振动信号经过ITD分解得到有效频带分量功率谱和有效频带分量,经过KICA处理得到独立频带分量功率谱,如图4所示。

图4 有效分量与独立分量功率谱Fig.4 Power spectrum of effective and independent components
由图4可知,有效分量包含了缸盖振动信号有效频带中的所有信息,但各分量仍存在频带混叠,导致微弱的故障敏感信息仍被覆盖。独立分量频带相互独立,对应不同的振源信号,根据缸盖振动信号的频带分布规律[3]可知:相对高频的前两个独立分量对应进排气门开启和落座冲击,相对低频的第3个独立分量则对应缸内气体燃爆冲击。于是,对进排气门系统故障和燃油系统故障敏感性不同的信号得到有效分离,从而将柴油机故障信息集中反映于敏感频带,增强了故障敏感特征。不同状态下的各独立分量的功率谱分布具有较大差别。
5 柴油机故障诊断试验
5.1 故障特征提取
AR(auto regression model,简称AR)模型的自回归参数对系统状态变化反应极为敏感[11],所以,分别提取3个独立分量的自回归参数作为特征参数。根据FPE准则确定3个独立分量的模型阶数分别为12,10,8。鉴于系统的状态主要由前几阶模型参数决定,因此选择前6阶的自回归参数和模型方差作为特征向量。
模糊熵(fuzzy entropy,简称FE)能够反映系统在不同运行状态下产生的信号的随机性、规律性和信息量的差异[8]。不同工况下的柴油机缸盖振动信
号具有不同的分布规律和信息量,因此分别提取3个独立分量的模糊熵作为柴油机故障诊断的特征参数。
当柴油机处于不同的运行状态时,缸盖振动信号的频率成分与能量分布表现出明显差异[1]。因此提出标准化能量矩[12](standardized energy moment,简称SEM)的概念,表征各独立分量的能量分布变化规律,并作为特征参数诊断柴油机故障。SEM的计算过程如下。
计算各独立分量能量矩为

(7)
其中:xi(t)(i=1,2,3)为独立分量。
标准化能量矩为
SEMi=Ei/En
(8)
其中:i=1,2,3;En表示正常工况下各独立分量能量矩之和。
5.2 故障分类试验
试验中,柴油机8种工况下的缸盖振动信号各采集120组,并利用本方法提取8种工况下的缸盖振动信号的特征参数。表1中列出4种典型工况下的特征参数,其中x1,x2,x3表示独立分量,φi1,φi2,…,φi6,σi,FEi,SEMi分别表示第i(i=1,2,3)个独立分量的前6阶自回归参数、模型残差方差、模糊熵和标准化能量矩,最终构建的特征子集维数为27维。由表1可知,同一工况下的不同独立分量的同类特征参数差别明显,说明各独立分量很好地反映了原信号的局部特征;不同工况下的各特征参数组合在分布空间和聚集性上也表现出明显的差别,说明不同工况下的特征向量具有良好的类间离散性。

表1 柴油机运行状态特征参数
选取特征参数φ32,FE1和SEM2组成特征向量,可有效区分各类故障,特征参数分布如图5所示。
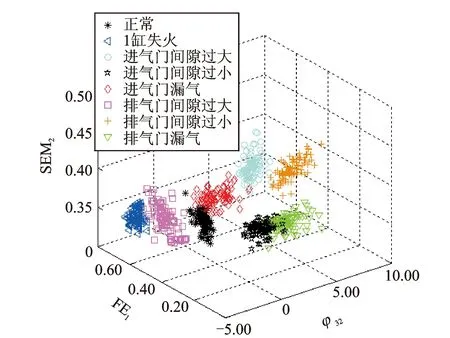
图5 SVESS-ITD-KICA后特征向量三维分布图Fig.5 Three-dimensional distribution of feature vectors after SVESS-ITD-KICA
为对比说明模型的有效性,分别提取SVESS-ITD-KICA和SVESS-ITD-ICA处理之后的特征参数φ32,FE1和SEM2组成特征向量,绘制其三维分布图如图6所示。

图6 特征向量三维分布图Fig.6 Three-dimensional distribution of feature vectors
比较图5和图6可知, 利用本研究方法提取的特征参数具有最佳的类内聚集性和类间离散性,这是因为本研究方法获取了独立特征频带,使得柴油机故障特征集中反映于敏感频带,增强了故障敏感信息。
为进一步说明该模型的诊断精度,将特征参数输入KELM进行分类试验。每种工况随机选取70组数据作为训练样本,其余50组数据作为测试样本,分别输入KELM进行训练和分类测试,其中核函数选择RBF核函数。3种特征提取方案下的测试结果如表2所示。
表23种特征提取方案下的故障诊断结果
Tab.2Faultdiagnosisresultsofthreefeatureextractionschemes

特征提取方案计算时间/s故障诊断精度%SVESS-ITD-ICA9.5645.61SVESS-EMD-KICA20.3572.45SVESS-ITD-KICA12.4199.65
由表2可以看出,SVESS-ITD-KICA的故障诊断精度最高,计算时间较短。进一步证明了该方法利用缸盖振动信号对柴油机进行故障诊断的有效性和准确性。
6 结 论
1) 奇异值能量标准谱解决了差分谱信噪分界点难以确定的问题,快速有效地消除了缸盖振动信号中的噪声,并增强了其振动冲击特征。
2) ITD计算速度快,分解精度高,将其用于缸盖振动信号的分解,能够快速准确地分离出信号中包含故障特征的有效频带。
3) 针对ITD分解仍存在部分频带混叠的问题,提出利用KICA消除频带混叠以分离故障敏感频带的方法,从而将柴油机故障特征信息集中反映于敏感频带,大大提高了特征参数辨识度。核极限学习机分类试验结果表明与基于EMD和ICA的分析方法相比,笔者所提方法极大地提高了柴油机故障诊断的速度和精度,故障诊断精度达到99.65%。
[1] 杜灿谊,杨志坚,丁 康. 小波分析在发动机失火监测中的应用[J]. 振动、测试与诊断,2011, 31(3):318-322.
Du Canyi, Yang Zhijian, Ding Kang.Monitoring method for engine misfire based on wavelet analysis[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(3):318-322. (in Chinese)
[2] 胡劲松,杨世锡,吴昭同,等. 基于EMD和HT的旋转机械振动信号时频分析[J]. 振动、测试与诊断,2004,24(2):106-110.
Hu Jingsong, Yang Shixi, Wu Zhaotong, et al. Time-frequency analysis of vibration signals in rotating machinery[J]. Journal of Vibration, Measurement & Diagnosis, 2004,24(2):106-110. (in Chinese)
[3] 尹刚,张英堂,李志宁,等. 基于 MSPCA 的缸盖振动信号特征增强方法研究[J]. 振动与冲击,2013,32(6):143-147.
Yin Gang, Zhang Yingtang, Li Zhining, et al.Fault feature enhancement method for cylinder head vibration signal based on multiscale principal component analysis[J]. Journal of Vibration and Shock,2013,32(6):143-147. (in Chinese)
[4] Han S, Kim H, Bae H. Extraction of rotating machine sources for fault diagnostics using independent component analysis [C]∥IEEE Instrumentation and Measurement Technology Conference. Ontario,Canada:Elsevier Ottawa, 2005:1507-1512.
[5] 尚柏林,谢紫龙,程 礼,等. EMD 与 ICA 相结合的复杂转子系统早期故障诊断[J]. 科学技术与工程,2014, 14(2):265-270.
Shang Bolin, Xie Zilong, Cheng Li, et al. Early fault diagnosis of complex rotor systems by EMD-ICA[J]. Science Technology and Engineering,2014,14(2):265-270. (in Chinese)
[6] 蔡连芳,田学民,张妮. 基于时序结构KICA和OCSVM 的过程故障检测方法[J]. 清华大学学报:自然科学版,2012,52(9):1205-1209.
Cai Lianfang, Tian Xuemin, Zhang Ni.Process fault detection method using time-structure KICA and OCSVM[J]. Journal of Tsinghua University: Science &. Technology,2012,52(9):1205-1209. (in Chinese)
[7] Frei M G, Osorio I. Intrinsic time-scale decomposition: time-frequency-energy analysis and realtime filtering of non-stationary signals[J]. Proceedings of the Royal Society A,2007,463(8):321-342.
[8] 罗颂荣,程军圣,郑近德,等. 基于ITD分形模糊熵的轴承早期故障诊断[J]. 振动、测试与诊断,2013, 33(4):706-710.
Luo Songrong, Cheng Junsheng, Zheng Jinde,et al. Incipient fault diagnosis based on ITD fractal dimension and fuzzy rntropy for bearings[J]. Journal of Vibration, Measurement & Diagnosis, 2013,33(4):706-710.(in Chinese)
[9] 田昊,唐力伟,田 广,等. 基于核独立分量分析的齿轮箱故障诊断[J]. 振动与冲击,2009, 28(5):163-164.
Tian Hao, Tang Liwei, Tian Guang, et al. Fault diagnosis of gearbox based on KICA[J]. Journal of Vibration and Shock,2009,28(5):163-164. (in Chinese)
[10] 胥永刚,谢志聪,孟志鹏,等. 基于奇异值分解的磁记忆信号特征提取方法[J].振动、测试与诊断,2014,34(6):1105-1109.
Xu Yonggang, Xie Zhicong, Meng Zhipeng, et al. Feature extraction method of magnetic memory signal based on SVD[J]. Journal of Vibration, Measurement & Diagnosis,2014,34(6):1105-1109. (in Chinese)
[11] 夏天,王新晴,肖云魁,等. 应用EMD-AR谱提取柴油机曲轴轴承故障特征[J]. 振动、测试与诊断,2010, 30(3):318-321.
Xia Tian, Wang Xinqing, Xiao Yunkui, et al. Feature extraction from crank-shaft bearing fault of diesel engine using empirical mode decomposition and auto regressive model spectrum technology[J]. Journal of Vibration, Measurement & Diagnosis,2010, 30(3):318-321. (in Chinese)
[12] 程军圣,李海龙,杨 宇,等. 改进ITD和能量矩在齿轮故障诊断中的应用[J]. 振动、测试与诊断,2013,33(6):954-959.
Cheng Junsheng, Li Hailong, Yang Yu, et al.Based on the improved ITD and energy moment to diagnose the gear[J]. Journal of Vibration, Measurement & Diagnosis,2013,33(6):954-959. (in Chinese)
国家自然科学基金资助项目(51305454)
2015-07-08;
2015-09-02
TH137; TK41.1

刘敏,男,1990年8月生,博士生。主要研究方向为机械设备测试技术与信号处理。曾发表《基于ITD和邻域差分能量算子解调的内燃机瞬时转速计算》(《车用发动机》2016年第2期)等论文。
E-mail:hunter1848@163.com

