基于统计模型进行率失真优化的加密图像压缩算法

冯阳，王春桃

(华南农业大学数学与信息学院，广东 广州 510642)

基于统计模型进行率失真优化的加密图像压缩算法

冯阳，王春桃

(华南农业大学数学与信息学院，广东 广州 510642)

如何对加密数据进行有效压缩和高质量重构是云计算环境中颇具挑战性的一个研究问题。其挑战性主要来自于云用户的加密操作掩盖了载体数据的统计特性，从而使得云端的压缩很难像常规压缩那样充分利用载体的统计特性。在小波系数统计模型吻合度评估的基础上，提出了一种基于统计模型进行率失真优化的加密图像压缩算法。将灰度图像经提升小波分解后的低频子带和小波子带分别进行流密码加密和置乱加密，然后再分别进行无损和有损压缩，最后进行相应的逆操作而重构原图像。鉴于充分的评估实验表明柯西分布能更良地表征图像小波系数，因此利用柯西分布来表征小波系数，并在此基础上利用率失真理论推导有损压缩用的最优量化步长。实验仿真结果表明，所提出的加密图像压缩算法能获得良好的压缩效率和重构质量，且能显著优于同类经典算法，并与常规的JPEG压缩算法性能相当甚至更好。

加密域信号处理；率失真优化；柯西分布；提升小波变换

随着大数据时代的来临，用户的图片、视频、音频的存储与共享越来越容易，但随之而来的数据隐私保护问题也引起了人们的担忧。为保护数据及其相关隐私信息，用户通常会运用加密算法对明文数据进行加密，但加密操作却会限制数据信号的进一步处理。为解决这些问题，国内外众多研究人员开展了加密域信号处理的广泛研究[1]。

加密域信号压缩是加密域信号处理的其中一个重要分支，主要应对云计算环境下信号的压缩与安全传输的问题。对于该问题，传统的做法是先对明文数据进行压缩处理，然后对压缩的数据进行加密，之后再将压缩及加密后的数据经由信道传送到接收方[2]。接收方则进行相应的逆处理，即先进行解密然后进行解压缩，从而有损或无损地恢复原始数据。然而，在云计算环境下，用户通常对云端不信任，因而在将数据传至云端前会进行数据加密；但鉴于用户的终端设备(如手机、移动设备等)处理能力有限，或者由于无利益驱动，用户不会在加密前进行数据压缩，而是直接把加密数据经由通信信道传至云端。尽管云端的存储空间很大，但相对日益成几何级数增长的海量数据，云端为节省存储空间和传输带宽，仍然非常有必要对用户的加密数据进行压缩。

由于加密操作通常会掩盖载体信号的统计特性，使得加密后的数据呈现出完全的随机性，因此云端无法像常规先压缩后加密的情形那样充分利用载体信号的统计特性，从而给加密信号的压缩带来严重的挑战。尽管直觉上完全随机的加密信号是无法进行压缩的，但Johnson等[3]利用信息理论证明，理论上这种新型的、先加密后压缩系统的压缩性能和安全性能与传统的先压缩后加密系统的性能一致。他们也分别给出了针对二值数据序列的无损及有损加密信号压缩算法[3]，表明了对加密信号进行压缩的可行性。在此基础上，众多研究人员开展了加密信号的压缩研究[4-9]。Schonberg等[4-5]利用LDPC对流密码加密的二值图像进行压缩，并利用LDPC解码实现原始数据的无损重构。Lazzereitt等[6]在加密前充分利用灰度图像不同位平面间以及彩色图像不同色彩分量间的统计相关性，进一步研究灰度/彩色图像的加密域压缩问题，较好地提升了压缩性能。与前人的做法不同，Kumar等[7]先利用预测器产生预测误差，然后再针对预测误差进行加密和压缩，由于这样充分利用了灰度/彩色图像的空间依赖特性，因此较为显著地提升了加密信号的压缩性能。Liu等[8]提出了一种递进式的加密灰度图像压缩算法，接收方利用已恢复的较低分辨率信号估计统计特征，进而利用该统计特征更好地重构较高分辨率的信号，如是迭代直至恢复原始图像，仿真表明该算法提升了加密压缩和重构性能。Zhou等[9]利用预测误差聚类和随机置乱加密的方式，获得了与针对未加密图像进行压缩的JPEG2000算法可比拟的性能。

与前述的加密信号无损压缩相应，加密信号的有损压缩亦得到了广泛的研究，以在可行重构质量的前提下获得更高的压缩率[10-20]。根据所采用的有损压缩方式不同，这些文献大致可以分为3类。其中，文献[10-12]采用压缩传感技术进行压缩，文献[13-17]采用量化方式进行压缩，文献[18-20]主要采用均匀下抽样方式进行压缩。对于第一类加密信号有损压缩算法，Kumar和Makur[10]提出用压缩传感矩阵去压缩加密数据，然后用修改的基追踪(basis pursuit，BP)算法进行原始信号的有损重构；Zhang等[11]用梯度投影矩阵来进行压缩；Song等[12]用训练学习得到的图像字典来对加密图像进行数据压缩，并用双字典超分辨率方法进行重构。对于第二类加密域压缩算法，Zhang[13]通过所设计的标量量化器将加密数据正交变换结果中过粗和过细的系数丢弃掉而实现高效压缩，检测端则利用迭代方法进行解压缩并恢复过粗和过细的系数。随后，Zhang等[14]提出把流密码加密的图像分解成若干部分，然后对每一部分进行量化压缩，进而构造了一种可伸缩的加密图像压缩算法。此外，他们把原始图像进行多层分解产生低分辨率子图像和预测误差，然后分别用流密码和置乱方式进行加密，并利用率失真理论选择最优的量化步长，构造了一种基于多层分解的加密图像压缩算法[15]。此外，Zhang等[16]在流密码加密前产生一些针对原图像的辅助信息，这样压缩方和接收方能通过这些辅助信息而提高压缩效率和重构性能。Wang等[17]利用提升小波分解原始图像，并分别用流密码和置乱方式对低频子带和小波系数进行加密，并利用启发式方式设置量化步长以对小波系数进行量化压缩。对于第三类加密域压缩算法[18-20]，主要采用均匀下采样的方法进行压缩，并在接收方利用不同的内容自适应插值方法重构原始图像。

上述众多文献中，文献[4-5]在接收方利用了马尔科夫特性而提升了二值图像的加密压缩和重构性能，文献[6-8]在加密前充分利用载体图像的统计相关性较好地提升了加密压缩性能；文献[15]通过置乱加密保持了载体信号的统计特性，进而利用率失真理论优化量化步长；文献[16]通过在加密前产生针对原图像的辅助信息，从而为压缩方优化量化步长和接收方提高重构性能提供了便利。这些表明，若能充分地利用载体信号的统计特性，则能有利于提高加密信号的压缩效率和重构性能。

受此启发，本文提出了一种利用统计模型进行率失真优化的加密图像压缩算法。本文首先利用提升小波对原始图像进行金字塔分解，然后对低频子带和小波系数分别进行流密码加密和置乱加密。获得这些加密系数后，云端对低频子带进行无损压缩；对加密的小波系数则用能很好地表征图像统计特性的柯西分布表征小波系数[21]，并基于率失真优化理论优化量化步长，进而利用该最优量化步长对小波系数进行有损压缩。接收方对低频子带进行无损解压缩，对小波系数进行反量化而重构加密小波系数；随后通过解密操作和逆提升小波变换重构原始图像。实验仿真结果表明，本文算法能获得良好的压缩效率和重构性能，比同类基于置乱加密的加密压缩算法性能好，并与常规的、针对未加密图像进行压缩的JPEG压缩算法性能相当或略好。

值得指出的是，尽管置乱加密会带来统计信息的泄露，但由于置乱系数的数量比较大，且包含图像主要信息的低频子带是流密码加密的，因此本文算法的安全性是可行的。此外，Kang等[22-23]的理论分析也表明，因置乱而泄露的信息约在log (n)量级，且知道统计分布后进一步的信息泄露随着n成指数级下降；其中，n为置乱系数的数量。

1 柯西分布及其参数估计方法

为了利用率失真理论对量化步长进行优化，本文采用能良好表征载体统计特征的柯西分布来表征图像小波系数。柯西分布，也称为柯西-洛伦兹分布，是以奥古斯丁·路易·柯西与亨德里克·洛伦兹名字命名的一种连续概率分布。该分布是一种数学期望不存在的连续型分布函数，其零均值概率密度函数为：

(1)

其中，μ是尺度参数，x代表柯西分布峰值位置与当前位置之差。由于μ不是柯西分布的均值和方差，因此μ值无法通过简单的均值和方差来计算得到，因而μ值的计算不太稳定，且难于收敛。

根据文献[24]，实际的μ值可按下列方式进行估计：首先取小波系数绝对值小于某个阈值Thresh(如Thresh=2)的所有小波系数，然后计算其累积分布Fx(|x|)(即小波系数绝对值|x|小于Thresh时的数目占总系数数目的百分比)，最后按下式来估计μ：

(2)

2 本文算法

本文提出的加密灰度图像压缩算法主要分为3个部分：加密、压缩和重构，如图1所示。其中，加密由用户(即载体拥有者)来完成，具体加密算法在2.1节中进行介绍；压缩由云端来实施，具体压缩算法在2.2节中进行介绍；原始图像重构在接收方完成，具体在2.3节中进行介绍。此外，压缩时用到的最优量化步长在2.4节进行介绍。

2.1 加密过程

本文算法中的加密过程如图2所示。设I(x,y)是大小为H×W的原始灰度图像。DC电平位移是一种减小图像小波变换后系数的动态范围的常用方法，如文献[25]中提出了一种彩色图像DC系数的自适应水印算法。本文中，先将I(x,y)进行一次DC电平位移，即将I(x,y)的每个像素都减去128，得到Ir(x,y)。接着对Ir(x,y)进行L(L>0)层的提升小波变换，每层分别获得4个子带LL、LH、HL和HH。对于低频子带LLL，采用流密码的方式进行加密；对于其他子带(小波子带)，采用置乱方式进行加密，详细加密过程如下。

1) 对低频子带LLL进行加密时，首先通过秘钥KLL生成一组范围为[0,2BitDepLL)的伪随机数序列Sc={Sc(k)|k=1,…,HW/22L}。

图1 本文算法流程图Fig.1 Block diagram of the proposed algorithm

图2 加密流程示意图，其中L为小波分解的层数，l=1,…,LFig.2 Illustration of encryption process, where L is the number of pyramid levels and l=1,…,L

其中BitDepLL为低频子带LLL的位深度，计算公式如下：

BitDepLL=|log2(2max(|max(LLL)|,

|min(LLL)|)+1)|

(3)

根据伪随机数序列Sc，对第L层的LLL子带进行如下的流密码加密：

EcLLL(k)=

mod (LLL(k)+2BitDepLL-1+Sc(k),2BitDepLL)

(4)

ecfl(k)=cfl(Dl(k))

(5)

完成上述所有的加密过程后，发送方将BitDepLL、EcLLL、ecfl发送给第三方。

2.2 压缩过程

为节约传输带宽和/或存储空间，第三方需要先对接收到的加密信息进行压缩。为了获得良好的压缩效率和重构质量，分别对EcLLL、ecfl进行两种不同的压缩方法，即对他们分别进行无损和有损压缩，压缩过程如图3所示。

对于无损压缩，直接用BitDepLL位对每个流密码加密的低频子带系数EcLLL(k)进行编码，得到加密压缩后的低频子带m_EcLLL。因此，该比特流长度为BitDepLL·HW/22L。

对于有损压缩，首先进行如下的量化：

q_ecfl(k)=

(6)

图3 压缩流程示意图Fig.3 Illustration of compression process

其中Δl代表第l层的量化步长，将在2.4节中通过率失真优化而获得。然后，对q_ecfl进行多符号的算术编码得到aq_ecfl，以进一步提高压缩效率。

压缩完成之后，第三方将m_EcLLL、aq_ecfl、BitDepLL、Δl及算术编码的符号数nsymsl传送给接收方。因此，总的压缩比特流长度为：

LENcmp=|m_EcLLL|+

(7)

其中，等式前两项为加密压缩序列的比特流长度，其它为相关参数的长度。因此，压缩率为：

(8)

2.3 重构过程

当接收方接收到加密压缩的比特流后，采用图4所示的方式重构原图像。

图4 重构流程示意图Fig.4 Illustration of reconstruction process

1) 重构低频子带LLL。首先按每BitDepLL位转换成一个整数的方法对m_EcLLL进行解压缩，得到加密后的低频子带d_EcLLL。然后，再按式(9)进行解密：

d_LLL(k)=

mod (d_EcLLL(k)-Sc(k),2BitDepLL)-2BitDepLL-1

(9)

2) 重构各层的小波子带系数。首先将接收到的nsymsl和aq_ecfl送入AC解码器对aq_ecfl进行解码，获得加密量化系数dq_ecfl。然后再对dq_ecfl进行反量化，即

d_ecfl(k)=sign(dq_ecfl(k))·

floor((|dq_ecfl)(k)|+ε)·Δl)

(10)

其中，ε∈[0,1]主要用于补偿因量化而带来的失真误差。接着，再对得到的d_ecfl(k)利用伪随机数序列进行解密，即：

d_cfl(k)=d_ecfl(Dl(k))

(11)

其中Dl是在排序操作的过程中生成的索引序列。

3) 当恢复出包含LLL和d_cfl的一维向量后，根据它们各层子带的大小而转化成二维子带。随后，进行逆提升小波变换和逆DC电平位移，得到重构图像Ir(x,y)。

2.4 量化步长最优化

如前所述，对加密的小波系数进行量化时需要用到量化步长。为在同等码率下获得最小的失真，本文利用率失真理论来最优化量化步长。率失真优化通常使用拉格朗日乘子法把约束优化问题转化为无约束优化问题，进而找出一个或者多个性能最优的相关参数集，使得在码率和图像失真之间达到一个最优的折中。视音频中的率失真优化方法通常只是在保持特定码率的前提下最小化失真，但鲜有根据率失真优化理论推导最优化的量化步长。为获得更优的加密图像压缩重构性能，本文用柯西分布良好地表征提升小波系数，并基于该分布利用率失真优化理论推导最优的量化步长，具体如下所述。

利用某一量化步长Δ(为简便起见，下面推导时将Δl的下标l略去)进行量化时，量化后的失真以及码率都是量化步长Δ的函数，分别记为D(Δ)和R(Δ)。根据率失真优化理论，最优的量化步长Δopt可以通过求解下列无约束优化问题而得到：

(12)

其中λ为拉格朗日乘子。式(12)经初等变换后有：

(13)

下面首先给出R(Δ)函数。若对量化之后的加密小波系数进行熵编码，那么R(Δ)将等于量化之后的加密小波系数的熵，即有

(14)

其中，P(iΔ)为量化幅度为iΔ时的概率，即

(15)

把式(1)代表的柯西分布代入式(14)，经过数学推导可得

(15)

类似地可得到失真函数D(Δ)函数。因采用标量量化，因此D(Δ)可定义为

(16)

把柯西分布代入式(16)，经过数学推导可得

(17)

基于公式(16)-(17)，我们进一步推导R(Δ)和D(Δ)关于Δ的偏导函数，有

(18)

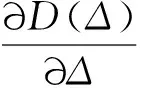
(19)

由于式(18)-(19)是非线性的，代入式(13)后难于直接获得Δopt的解析表达式。为此，我们不直接推导Δopt的解析表达式，而是基于式(13)、(18)和(19)采用数值方法来搜索最优的Δopt。为提高搜索效率，本文采用二分搜索法进行Δopt的搜索。对于给定的λgvn，每一层的最优量化步长都需满足式(13)，具体搜索算法如下：

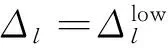
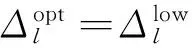
3 实验结果

本节通过实验仿真的方法对本文提出的加密压缩算法进行性能评估。实验中，我们测试了50幅具有不同纹理特性的、大小为512×512的灰度图像。图5示例了其中的10幅测试图像，包括Peppers、Lena、Man、Goldhill、Sailboat、Tank、Zelda、Woman、Elain和Girl。

图5 其中10幅实验用测试图像Fig.5 Illustration of 10 test images

根据我们之前的研究工作[17]，当设置提升小波为CDF2.2和金字塔分解层数L=4时，具有较好的压缩和重构性能。此外，这种设置也具有较好的可行安全性能，即尽管存在统计信息的泄露，但敌手要想通过穷举尝试方法来恢复置乱加密的小波系数时，所需要的计算复杂度实际中是不可行的[17]。再者，本算法对图像的重要关键信息——低频子带进行了流密码加密，在“一次一密”的情况下，敌手在未掌握密钥时是无法恢复低频子带信息的，进而难于重构原始图像。因此，低频子带的流密码加密和小波子带的置乱加密结合，是具有实际可行的安全性的。尽管这样发送端需要进行除加密以外的提升小波变换，但由于提升小波变换具有可实时操作的低复杂性，因而只是给发送端增加了少量的额外负担，实际中是可行的。

本文继续采用文献[17]中的设置来进行实验仿真。性能评估时，我们采用每像素的位数(bpp)和重构图像的峰值性噪比(PSNR)作为衡量指标。其中，bpp用式(8)进行计算，PSNR采用式(20)进行计算：

(20)

其中，H和W分别表示图像的长和宽。为了评估不同质量的重构图像，我们利用上述参数，并设置λgvn为4、30、500和6 500。我们根据第1节给出的算法对测试图像Goldhill进行加密、压缩和重构，得到的重构图像如图6所示。其中，也给出了压缩码率和重构PSNR值。如图可知，本文算法能够得到较好的重构质量，即便在PSNR低至30 dB左右时，仍然具有较可行的视觉质量(如图6(d)所示)。

为进一步评估本文算法的压缩与重构性能，本文算法与Zhang算法[13]及JPEG算法进行bpp-PSNR性能对比。其中，Zhang算法是直接采用置乱方式进行加密的加密压缩算法中比较经典的算法，JPEG算法是指对未进行加密的图像进行压缩的常规压缩算法。实验时，本文算法的λgvn采用如下范围值：

λgvn∈{0,1.5,8}∪{20,40,120}∪

{250,500,800}∪{1 200,1 600,2 000}

Zhang算法采用如下参数：Δ=60,M=3,5,…,11,α=0.15，其中Δ=60是文献[13]中建议的参数，M是量化压缩参数，α是未压缩的“刚性像素”的比例；JPEG压缩的参数设置为：QF∈{10,40,70}∪{90,91,…,100}。

4 总 结

本文提出了一种基于统计模型进行率失真优化的加密图像压缩算法。发送方首先将DC电平位移后的灰度图像进行多层的提升小波变换，然后对低频子带和小波子带分别进行流密码加密和置乱加密。接收到加密数据后，第三方对低频子带直接进行无损压缩，对小波子带进行量化压缩和算术编码。在获得加密和压缩的数据后，接收方先后进行解压缩、解密、逆提升小波变换以及逆DC电平转换等操作而重构原始图像。此外，本文评估了柯西分布、拉普拉斯分布和一般高斯分布这三种经典统计模型对灰度图像小波系数的表征能力，充分的实验仿真结果表明，3种模型中柯西分布能最好地表征小波系数。基于此，本文采用柯西分布表征小波子带系数，然后再用率失真优化理论推导最优量化步长。实验仿真结果表明，本文算法具有良好的压缩效率和重构性能，显著优于同类经典置乱加密图像压缩算法性能，并与常规的JPEG压缩算法性能相当或更好。

图6 不同λgvn时Goldhill图像重构结果示意图Fig.6 Illustration of reconstructed images under different λgvn, where the CR denotes compression rate

图7 三种不同加密压缩算法针的bpp-PSNR性能比较Fig.7 Rate-PSNR performance comparison for the proposed scheme, ZHANG and JPEG

[1] ERKIN Z, PIVA A, KATZENBEISSER S, et al. Protection and retrieval of encrypted multimedia content: When cryptography meets signal processing [J]. Eurasip Journal on Information Security, 2007, 2007(1): 17.

[2] 张德丰, 马莉, 范灵，等. 基于小波图像压缩技术的算法研究[J]. 中山大学学报(自然科学版), 2008, 47(2): 42-45.

ZHANG D F, MA L, FAN L, et al. Algorithm research on image compression technologies with wavelet transform [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2008, 47(2): 42-45.

[3] JOHNSON M, ISHWAR P, PRABHAKARAN V, et al. On compressing encrypted data [J]. IEEE Transactions on Signal Processing, 2004, 52(10): 2992-3006.

[4] SCHONBERG D, DRAPER S, RAMCHANDRAN K. On blind compression of encrypted correlated data approaching the source entropy rate [C]∥Proc 43rd Annu Allerton Conf, 2005: 1-4.

[5] SCHONBERG D, DRAPER S, RAMCHANDRAN K. On compression of encrypted images [C]∥Proc IEEE Int Conf Image Process, 2006: 269-272.

[6] LAZZERETTI R, BARNI M. Lossless compression of encrypted grey-level and color images [C]∥Proc 16th Eur Signal Processing Conf, 2008: 1-5.

[7] KUMAR A, MAKUR A. Distributed source coding based encryption and lossless compression of gray scale and color images [C]∥Proc IEEE 10th Workshop Multimedia Signal Processing, 2008: 760-764.

[8] LIU W, ZENG W, DONG L, et al. Efficient compression of encrypted grayscale images [J]. IEEE Trans on Signal Process, 2010, 19(4): 1097-1102.

[9] ZHOU J, LIU X, AU O, et al. Designing an efficient image encryption-then-compression system via prediction error clustering and random permutation [J]. IEEE Trans. on Inf Forensics and Security, 2014, 9(1): 39-50.

[10] KUMAR A, MAKUR A. Lossy compression of encrypted image by compressing sensing technique [C]∥ Proc TENCON 2009 IEEE Region 10 Conf, 2009: 1-6.

[11] ZHANG X, REN Y, FENG G, et al. Compressing encrypted image using compressive sensing [C]∥ Proc 7th Int Conf Intelligent Information Hiding and Multimedia Signal Processing, 2011: 222-225.

[12] SONG C, LIN X, SHEN X. Secure and effective image storage for cloud based E-healthcare systems [C]∥Proc IEEE Globecom 2013, 2013 : 653-658.

[13] ZHANG X. Lossy compression and iterative reconstruction for encrypted image [J]. IEEE Trans on Inf Forensics Security, 2011, 6(1): 53-58.

[14] ZHANG X, FENG G, REN Y, et al. Scalable coding of encrypted images [J]. IEEE Trans on Image Process, 2012, 21(6): 3108-3114.

[15] ZHANG X, SUN G, SHEN L, et al. Compression of encrypted images with multilayer decomposition [J]. Multimed Tools Appl, 2013, 78(3): 1-13.

[16] ZHANG X, REN Y, SHEN L, et al. Compressing encrypted images with auxiliary information [J]. IEEE Trans on Multimedia, 2014, 16(5): 1327-1336.

[17] WANG C, NI J. Compressing encrypted images using the lifting scheme [C]∥Proc 11th Int Conf Intelligent Information Hiding and Multimedia Signal Processing, 2015.

[18] KANG X, PENG A, XU X, et al. Performing scalable lossy compression on pixel encrypted images [J]. Eurasip Journal on Image and Video Processing 2013, 2013: 1-6.

[19] HU R, LI X, YANG B. A new lossy compression scheme for encrypted gray-scale images [C]∥ Proc of Intl Conf on Acoustic, Speech and Signal Processing 2014, 2014: 7387-7390.

[20] ZHOU J, AU O, ZHAI X G, et al. Scalable compression of stream cipher encrypted images through context-adaptive sampling [J].IEEE Trans on Inf Forensics and Security, 2014, 9(1): 39-50.

[21] KAMACI N, ALTUNBASAK Y, MERSEREAU R M. Frame bit allocation for the H.264_AVC video coder via Cauchy-density-based rate and distortion models [J]. IEEE Trans on Circuit System and Video Tech, 2005, 15(8): 994-1006.

[22] KANG W, LIU N. Compressing encrypted data and permutation cipher [J]. Computer Science, 2014:1-17.

[23] KANG W, LIU N. Compressing encrypted data: a permutation approach [C]∥Proceedings of the 50thAnnual Allerton Conference on Communications, Control and Computing, 2012: 1.

[24] 谢小兰. DCT域分布式视频编码中相关噪声模型研究[D]. 广州：华南理工大学, 2013.

XIE X L. Research on correlation noise model in DCT domain distributed video coding [D]. Guangzhou: South China University of Technology, 2013.

[25] 王员根，梁凡，肖明明. 一种彩色图像DC系数的自适应水印算法[J]. 中山大学学报(自然科学版), 2010, 49(4): 43-48.

WANG Y G, LIANG F, XIAO M M. Color image watermarking adaptively in DC coefficients [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2010, 49(4): 43-48.

Acompressionschemeonencryptedgreyimagesexploitingthestatisticmodelandratedistortingoptimization

FENGYang,WANGChuntao

(College of Mathematics and Informatics, South China Agricultural University, Guangzhou 510642, China)

How to compress encrypted data effectively and reconstruct it in a high quality way is a challenging research problem in the cloud computing environment. The challenge mainly comes from the encryption by cloud users, which masks statistical characteristics of cover data and thus makes the compression of encrypted data in the cloud side unable to fully exploit the statistical characteristics in a traditional way. Based on the fitness evaluation of statistical models in characterizing wavelet coefficients, a new compression scheme is proposed on encrypted grey images, which leverages the statistic model and rate distortion optimization. The coarsest subband and the other wavelet subbands generated through lifting wavelet decomposition of grey image are encrypted by stream and permutation ciphers, respectively. They are then compressed in lossless and lossy ways, respectively. The receiver finally performs the inverse operations to reconstruct the original image. As sufficient tests show that the Cauchy distribution can well characterize wavelet coefficients, the Cauchy distribution is adopt to represent wavelet subbands. Via this statistical model, the rate-distortion theory is further used to derive optimal quantization steps for lossy compression. Experimental results show that the proposed algorithm can obtain better compressing efficiency and reconstruction quality. Also, it is significantly better than other permutation-based prior arts, and it is comparable to or even better than the conventional JPEG compression algorithm.

compression of encrypted image; rate distorting optimization; Cauchy distribution; lifting wavelet transform

TP309.7

A

0529-6579(2017)05-0064-10

10.13471/j.cnki.acta.snus.2017.05.009

2016-12-16

国家自然科学基金(61202467，61672242)

冯阳(1993年生)，男；研究方向多媒体信息安全；E-mail: szufengyang@gmail.com

王春桃(1979年生)，男；研究方向：加密域信号压缩、多媒体信息安全；E-mail：wangct@scau.edu.cn