静止卫星小推力多圈转移轨道间接优化

沈红新，李恒年

(西安卫星测控中心宇航动力学国家重点实验室，西安 710043)

静止卫星小推力多圈转移轨道间接优化

沈红新，李恒年

(西安卫星测控中心宇航动力学国家重点实验室，西安 710043)

本文研究了电推进平台地球静止(GEO)卫星转移轨道优化问题。在动力学模型中考虑了地球J2项摄动，基于庞特里压金极大值原理(PMP)推导了时间最优变轨控制律及其一阶必要性边界条件，采用推力幅值延拓技术和牛顿下山法对最优控制两点边值问题求解。仿真算例表明本文方法的有效性，相对已有结果性能指标可以提升5%左右。分析了静止卫星小推力多圈时间最优转移轨道要素变化特性，可供工程实际参考。

电推进; 地球静止卫星；间接法；两点边值问题；轨道优化

0 引 言

随着电推进技术的成熟发展，电推进技术的应用逐渐从位置保持向完成整个轨道转移控制任务转变。2012年3月，波音卫星系统公司在一次商业通信卫星竞标中推出了全球首款全电推进平台——BSS702SP平台，采用该平台，亚洲广播卫星-3A和欧洲通信卫星-115B在2015年3月1日由猎鹰9号火箭以一箭双星方式成功发射[1]。以往传统的做法是火箭将静止卫星发射到地球同步转移轨道(Geosynchronous transfer orbit, GTO)以后，通常采用化学推进发动机在远地点进行3～5次变轨可以将地球同步转移轨道变成地球静止轨道(Geostationary orbit, GEO)。如果用电推进代替化学推进，由于电推进高比冲的特点，可以节省大量燃料。但电推进系统推力很小，一般只有几百毫牛，远远小于化学推进的几百牛，因而采用电推进从GTO变轨至GEO的时间将长达数月，且变轨策略与化学推进的策略有很大区别。

地球静止卫星轨道转移是一类经典问题，很多学者对此进行了大量研究，但以往的研究大多针对的情况是推力比较大，轨道转移圈次只有几十圈的情况，例如文献[2-3]，或者利用月球近旁转向技术以节省发射地球静止卫星的速度增量[4]。以目前电推进系统的水平，推力还不能达到几牛的量级。由于初值估计偏差随时间的传播和累积，一般来说轨道转移时间越长、圈次越多，优化难度越大。因此很多学者将转移轨道根数进行均化处理，主要的工作见文献[5-7]，这样得到的解对估计时间和燃料消耗固然有意义，但也会一定程度上降低轨道动力学模型的准确性。另外一种近似估计全电推进GEO卫星转移时间和燃料消耗的方法是解析法[8-9]，但是这类方法是基于小偏心率的假设，因此只适用于低地球轨道(LEO)向GEO转移的情况。针对推力大小更接近实际的情况(1 N以下)，田百义等[10]基于李雅普诺夫优化原理进行了GTO-GEO转移轨道的优化设计。Graham和Rao[11]采用伪谱法优化多圈静止卫星转移轨道，伪谱法本质上是配点法的一种，解的最优性只能事后验证。

目前，在非线性最优控制领域主要有两大类数值方法：直接法和间接法[12-14]。直接法一般采用参数化方法将连续空间的非线性最优控制问题转换成离散空间的非线性规划问题，虽然它具有容易实现和收敛半径较大的优点，但是直接法不能保证所获的解的最优性。相对地，间接法主要是构造和求解由最优控制的一阶必要条件得到的Hamilton边值问题，其优点是：1)构造边值问题而不是参数优化问题，理论上能够准确快速获得最优解；2)由于采用最优控制理论(这里主要指变分法和极大值原理)，间接法能够提供优化问题必要的理论信息。但间接法也有其缺点，获得最优性条件的过程复杂繁琐，而且收敛半径较小[14]。本文利用间接法研究静止卫星最短时间小推力多圈转移轨道，推导了一阶最优性必要条件，采用牛顿下山法和推力幅值延拓方法求解两点边值问题，求解结果和文献中相同算例对比结果表明，性能指标可以提升5%左右。

1 动力学模型

电推进系统可以提供的推力加速度在10-4m/s2的量级，与自然摄动加速度的量级相当，因此可以将电推进加速度和摄动加速度统一处理。本文采用高斯摄动方程作为轨道控制模型，形式如下[3]：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

式中自变量定义为：

(8)

ex=ecos(ω+Ω)

(9)

ey=esin(ω+Ω)

(10)

ix=tan(i/2)cosΩ

(11)

iy=tan(i/2)sinΩ

(12)

L=Ω+ω+θ

(13)

为了简化公式形式，定义中间变量

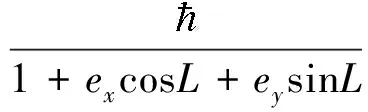
(14)

X=ixsinL-iycosL

(15)

(16)

式中：a、e、i、Ω、ω和θ分别表示轨道半长轴、偏心率、倾角、升交点赤经、近地点幅角和真近点角，μ为地球引力常数，m表示卫星质量，c表示推力器比冲Isp和地面重力加速度ge的乘积。fR、fT和fN分别表示径向、切向和法向加速度，其中包含发动机推力加速度和地球J2项摄动加速度，即fR=fr+frJ2，fT=ft+ftJ2，fN=fn+fnJ2，其中发动机推力加速度为

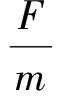
(17)

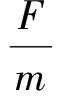
(18)

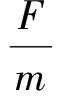
(19)

式中：F为发动机推力大小，α和β表示推力方向角，定义推力方向角β为推力矢量与轨道面的夹角，推力方向角α为推力矢量在轨道面内投影与地心矢径方向的夹角。地球J2项摄动加速度在径向、切向和法向的分量如下：

(20)

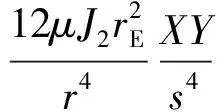
(21)

(22)

2 最优控制律及边界条件

假设初始轨道为GTO，初始轨道根数已知，目标轨道为GEO，要求目标轨道的偏心率和倾角为0，半长轴为42164 km。性能指标是转移时间最短，写为最大化性能指标为

φ=-tf

(23)

利用式(1)～(7)定义Hamilton函数

(24)

整理式(24)可得

H=λR(fr+frJ2)+λT(ft+ftJ2)+

(25)

式中：

(26)

(27)

λN= -λexnXey+λeynXex+

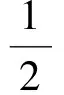
(28)

根据极大值原理[15]，最优控制律应使得H最大，因此最优推力控制为

(29)

(30)

(31)

式中：Fmax表示推力最大值。据此Hamilton函数可以再次重写为

(32)

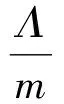
由式(23)得

Hf=1

(33)

如果终端相位不作约束，则

λL f=0

(34)

此外，终端质量不作约束，因此

λm f=0

(35)

3 两点边值问题求解算法

常用的边值问题求解方法是打靶法。打靶法通过求解一系列初值问题来获得边值问题的解。如果给定了积分初值，积分常微分方程(Ordinary differential equation,ODE)后检查边界条件的满足程度，再利用迭代算法逐步减小偏差。积分算法采用变步长Adams积分，具体算法见文献[16]。Colasurdo和Pastrone[17]设计了利用解析梯度的Newton法。本文的边值问题求解器综合了Colasurdo和Pastrone的理论成果和Newton下山法[18]。

首先对自变量进行无量纲化，可以降低迭代算法的收敛难度。不失一般性，第j段的时刻t通过下式进行转换

(36)

状态和协变量的ODE也随自变量作如下变换

(37)

式中：τj=tj-tj-1。为了简洁，把所有的因变量写在单独的向量中，同时为了给出一般表达式，把常因变量也包含在内

(38)

为了方法的通用性引入常因变量y，对应ODE有dy/dε=0。

边值问题的微分方程可以表示为

(39)

用矢量p表示未知初值，设p的初始解为p0，令z0=p0。给定初始解后，第r次迭代参数变化为

pr+1=pr+Δp

(40)

式中参数变化的大小Δp可以通过下式求得

(41)

式中：Ψ表示状态或者协变量的等式边界条件，注意到在迭代过程中Ψ可能不等于0，通过搜寻初值p使Ψ等于0。对[∂Ψ/∂p]可以用数值或解析的方式求逆。考虑到可以分解矩阵[∂Ψ/∂p]为

(42)

式中：矩阵[∂Ψ/∂s]可通过对边界条件求导获得。注意到s对应边界点的z，[∂s/∂p]即是边界点的[∂z/∂p]，而[∂z/∂p]满足

(43)

积分式(43)的齐次微分方程可以获得[∂z/∂p]，进而得到[∂s/∂p]。

经典的Newton迭代法具有二次收敛速度，但是十分依赖于初始值的选取。参考Newton下山法的思想，采取两种措施来降低迭代发散的几率：1)当Ψr+1>2Ψr时，令

pr+1=pr+Δp/2

(44)

2)在迭代格式中引进一个小于等于1的系数，即

(45)

式中:K称为下山因子，选取0.01≤K≤1。随着迭代过程逐步接近最优解时，可逐步提高K的值。Newton下山法的实质是以降低收敛速度为代价来提高算法鲁棒性，尽管如此，其收敛速度也比较快。

为了进一步降低多圈转移两点边值问题求解难度，先从推力大的轨道开始求解，这样轨道转移圈次少，转移时间较短，采用牛顿下山迭代法边值问题更容易收敛。以大推力轨道解作为初值，将推力幅值不断减小逐步求解(即推力幅值延拓)，每次延拓的边值问题都利用牛顿下山迭代法求解，通常经过十步左右可以求解得到实际推力的电推进转移轨道。采用i5处理器主频2.5 GHz CPU个人电脑编写的Fortran程序，每次推力延拓迭代时间大约几分钟。

4 仿真校验

卫星采用全电推进方式由GTO向GEO转移，优化的性能指标为时间最短。假设卫星推力大小为800 mN或者350 mN，比冲3500 s。初始轨道GTO和目标轨道GEO参数如表1所示。此算例来自文献[10]。

表1 GTO-GEO初始轨道和目标轨道参数Table 1 Initial and final orbits for GTO-GEO transfer

当最大推力为800 mN时，初始加速度2×10-4m/s2，剩余质量3721 kg，飞行时间138.4天，比文献[10]中148.8天的结果节省10天，性能指标提升约6.7%。轨道参数变化如图1所示。近地点高度全程增加，远地点高度先增加再降低；半长轴增加的速率先快后慢，倾角减小速率先快后慢，偏心率减小速率则先慢后快。特别值得指出的是倾角的变化速率曲线是向下凹的形式，这有些类似最速下降线路径的变化趋势，这可能是由于随着轨道能量越来越大，改变轨道面的效率也逐渐下降，仿真中发现一些次优的结果往往呈现倾角速率曲线向上凸的变化。

由于未对动力学方程作均化处理，轨道要素变化图放大观察可以见到其短周期变化，见图2。最大推力800 mN变轨的三维轨道位置变化如图3所示，根据L的变化可知大约经过197圈的变轨，远地点高度仍然有一个先增加再降低的过程。该图是将优化后的轨道位置速度数据输入STK软件后得到的分辨率较高的三维仿真演示画面截图。

图4和图5给出了最优轨道的平经度协变量和质量协变量随时间变化图，根据式(34)和式(35)所描述的最优性条件，在终端时刻λL f=0，λm f=0，由图4～5可知，最优轨道满足上述条件。

当推力为350 mN时，初始加速度0.875×10-4m/s2，剩余质量3715 kg，飞行时间322.7天，比文献[10]中338.9天结果节省15天，性能指标提升约4.5%。根据L的变化可知整个过程大约经过了452圈的变轨，大约是800 mN转移轨道圈次的两倍多。半长轴、倾角和偏心率等参数变化规律与图1中800 mN情况类似，限于篇幅这里不再给出轨道参数变化曲线。推力方向角变化如图6所示，推力方向角变化存在周期性规律，这点从局部放大图中更容易观察，从图6的局部放大图可以看出,推力方向角的变化周期接近半天。

需要指出的是，目前的动力学模型中只考虑了地球J2项摄动，虽然在卫星多圈转移过程中日月引力摄动、太阳光压摄动对卫星半长轴、倾角和偏心率都有不可忽视的影响，然而在长时间转移过程中考虑全摄动模型从工程角度来说并无必要，这固然是由于采用全摄动模型设计长时间多圈转移轨道十分困难，同时也因为控制执行过程中推力大小和方向的标定等也不可避免地存在误差累积，因此目前的多圈轨道设计的任务是将卫星送到近同步轨道，对卫星重新进行精确轨道确定之后，在之后的定点捕获阶段将卫星准确控制到指定位置。定点捕获阶段转移时间一般只有几天，采用解析摄动模型分析即可，具体模型可参见文献[19]。

5 结 论

对于利用电推进的小推力多圈地球静止轨道卫星转移轨道优化问题，本文利用极大值原理给出了最优控制律所应满足的微分方程和边界条件，按照这种方法设计，可以在收敛的前提下从理论上保证得到的解是最优解。文中给出的仿真实例说明了该方法的有效性，并且指标优于已有结果。

GTO-GEO多圈转移一般先增加远地点高度，然后再降低，这样可以在轨道速度更低的地方调整轨道面，降低调整轨道面的燃料消耗。最短时间的多圈转移轨道全程开机，主要轨道根数全程调整，描述轨道形状和大小的轨道根数不存在持续不变的情况。

[1] 段传辉，陈荔莹. GEO卫星全电推进技术研究及启示[J]. 航天器工程, 2013, 22(3): 99-104. [Duan Chuan-hui, Chen Li-ying. Research and inspiration of all- electric propulsion technology for GEO satellite[J]. Spacecraft Engineering, 2013, 22(3): 99-104.]

[2] Yue X, Yang Y, Geng Z. Indirect optimization for finite-thrust time-optimal orbital maneuver[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(2): 628-634.

[3] Gao Y. Advances in low-thrust trajectory optimization and flight mechanics[D]. Columbia: University of Missouri-Columbia, 2004.

[4] 曾国强，郗晓宁，任萱. 月球近旁转向技术研究[J]. 宇航学报, 2000, 21(4): 107-110. [Zeng Guo-qiang, Xi Xiao-ning, Ren Xuan. A study on lunar swing-by technique[J]. Journal of Astronautics, 2000, 21(4): 107-110.]

[5] Kluever C A. Geostationary orbit transfers using solar electric propulsion with specific impulse modulation[J]. Journal of Spacecraft and Rockets, 2004, 41(3): 461-466.

[6] Kluever C A, Oleson S R. Direct approach for computing near-optimal low-thrust Earth-orbit transfers[J]. Journal of Spacecraft and Rockets, 1998, 35(4): 509-515.

[7] Edelbaum T N. Propulsion requirements for controllable satellites[J]. ARS Journal, 1961, 31: 1079-1089.

[8] Kechichian J A. Reformulation of Edelbaum’s low-thrust transfer problem using optimal control theory[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(5): 988-994.

[9] Casalino L, Colasurdo G. Improved Edelbaum’s approach to optimize low Earth geostationary orbits low-thrust transfers[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(5): 1504-1510.

[10] 田百义，雪丹，黄美丽. 全电推进GEO卫星的变轨策略研究[J]. 航天器工程, 2015, 24(2):7-13. [Tian Bai-yi, Xue Dan, Huang Mei-li. Orbit transfer strategies for GEO satellites using all-electric propulsion[J]. Spacecraft Engineering, 2015, 24(2): 7-13.]

[11] Graham K F, Rao A V. Minimum-time trajectory optimization of multiple revolution low-thrust Earth-orbit transfers[J]. Journal of Spacecraft and Rockets, 2015, 52(3): 711-727.

[12] 雍恩米, 陈磊, 唐国金. 飞行器轨迹优化数值方法综述[J]. 宇航学报, 2008, 29(2): 397-406. [Yong En-mi, Chen Lei, Tang Guo-jin. A survey of numerical methods for trajectory optimization of spacecraft[J]. Journal of Astronautics, 2008, 29(2): 397-406.]

[13] 李俊峰, 蒋方华. 连续小推力航天器探测轨道优化方法综述[J]. 力学与实践, 2011, 33(3): 1-6. [Li Jun-feng, Jiang Fang-hua. Survey of low-thrust trajectory optimization methods for deep space exploration[J]. Mechanics in Engineering, 2011, 33(3): 1-6.]

[14] Betts J T. Survey of numerical methods for trajectory optimization[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(2): 193-207.

[15] Bryson A E, Ho Y C. Applied optimal control[M]. Washington, DC: Hemisphere, 1975.

[16] Shampine L F, Gordon M K. Computer solution of ordinary differential equations: the initial value problems[M]. San Francisco: Freeman, 1975.

[17] Colasurdo G, Pastrone D. Indirect optimization method for impulsive transfer[R]. AIAA Paper 1994-3762, 1994.

[18] 沈红新. 基于解析同伦的月地应急返回轨迹优化方法[D]. 长沙：国防科技大学. 2014. [Shen Hong-Xin. Optimization method for the Moon-Earth abort return trajectories based on analytic homotopic technique[D]. Changsha: National University of Defense Technology, 2014.]

[19] 李恒年. 地球静止卫星轨道与共位控制技术[M]. 北京：国防工业出版社, 2010:173-190.

IndirectOptimizationofLow-ThrustMulti-RevolutionOrbitTransfersforGeostationary-OrbitSatellites

SHEN Hong-xin, LI Heng-nian

(State Key Laboratory of Astronautic Dynamics, Xi’an Satellite Control Center, Xi’an 710043, China)

A method for the optimization of geostationary orbit (GEO) satellite orbit transfer with all-electric propulsion is proposed. The Earth’s oblateness (J2) perturbation is included in the dynamic model. The time-optimal control law of the GEO satellites as well as the first order optimality necessary conditions, based on the Pontryagin’s maximum principle (PMP), are deduced. The resulting two-point boundary value problem is solved based on thrust continuation approach and by means of the Newton’s downhill method. Numerical simulations have demonstrated the effectiveness of the approach proposed, with performance increasing about 5% compared to the existing results. From the numerical results, some characteristics of the time-optimal transfer orbit element changes are drawn, which could provide reference for aerospace engineering.

Electric propulsion; Geostationary-orbit satellite; Indirect method; Two-point boundary value problem; Trajectory optimization

V412.4

A

1000-1328(2017)10- 1041- 07

10.3873/j.issn.1000-1328.2017.10.004

2017- 05- 11;

2017- 08- 10

国家自然科学基金(11702330)

沈红新(1986-)，男，博士，工程师，主要从事航天器轨道姿态最优控制研究。

通信地址：西安505信箱28分箱(710043)

电话：(029)84762520

E-mail:shxnudt@163.com