具有高适应性的光纤陀螺零偏非线性温度误差补偿方法

卓 超，杜建邦

(1. 北京航天自动控制研究所，北京 100854；2. 宇航智能控制技术国家级重点实验室，北京 100854)

具有高适应性的光纤陀螺零偏非线性温度误差补偿方法

卓 超1,2，杜建邦1,2

(1. 北京航天自动控制研究所，北京 100854；2. 宇航智能控制技术国家级重点实验室，北京 100854)

确定了光纤陀螺零偏温度误差模型的组成并设计温度试验验证了所选模型项的充分性。通过反解温箱传递函数实现了温箱的输入控制，并控制陀螺本体进行了恒定速率升降温，再结合不同高低温区间的温度循环操纵误差轨线完成了对于温度/温变速率平面的覆盖，揭示了平面覆盖性与环境适应性间的联系。借助非线性偏最小二乘估计对零偏非线性温度漂移模型进行了高精度辨识，获得了各温度因素的组成形式与影响权重。最后利用随机变温与惯导冷启动试验验证了本方法对于复杂温度环境的高适应性。经温度误差补偿后，全温范围陀螺零偏稳定性由0.02°/h水平降至优于0.005°/h。

光纤陀螺; 零偏温度误差; 温度试验设计; 非线性偏最小二乘

0 引 言

光纤陀螺以其工作原理的先进性和制作工艺的不断成熟获得了越来越广泛的应用，性能优势也日益体现。由光纤陀螺组成的惯性导航系统精度正在从导航级向战略级迈进，使之成为了激光陀螺，甚至静电陀螺有力的竞争对手，引领了惯性技术领域的发展方向[1-3]。作为光纤传感器，光纤陀螺输出易受温度影响，同时光纤惯导所需工作温度范围宽，使用环境中温度场分布空间上具有非均匀性，时间上具有时变、随机性。这些使得以零偏漂移为代表的温度效应误差成为了制约纯惯性导航精度提高的主要因素[4-5]。

在系统级应用层面，通过试验设计与误差建模对陀螺温度漂移进行实时准确补偿是提高光纤惯导环境适应性的一项关键技术而受到越来越广泛的重视。国外惯导生产厂商已开展了大量研究工作，取得了良好的工程使用效果，但没有公开相关方法，只简要介绍了补偿结果[6-7]。在已公开资料中，一般方法是采用单温度传感器多项式模型[8]，通过增加多项式阶数来提高拟合质量，这通常只能满足中低精度补偿需求，有时甚至会恶化补偿结果。文献[9]通过安装在光纤陀螺与惯导壳体上的双测温传感器获得了不同恒定温度点的静态温度差与变温过程中的动态温度差。利用这两部分的多项式组合对陀螺温度漂移进行了拟合。文献[10]则通过均匀分布在光纤环上的八个温度传感器将温度场空间梯度引入模型，并利用多项式插值对零偏进行了补偿。文献[11-12]在考虑温度一阶导数的同时，引入了二阶导数作用，以更好地描述升降温过程中不同的误差特性。从以上思路可以看出，零偏温度漂移作为典型的非线性过程，采用简单的线性误差模型远远不够，但使用多传感器融合来提高输入输出的相关性通常基于主观试凑而缺乏明确的物理意义，且多点传感器的优化布放与相关性搜寻需要通过大量试验获得并占用较多硬件资源，对补偿效果的提升也相对有限。另外，在模型中引入高阶导数则增加了系统噪声和启动时间。针对上述不足，为进一步增强对非线性模型的描述能力，一些智能方法[13-15]已用于零漂模型的建立，但这些算法较为复杂，不利于实时处理，同时由于只采用基本的温箱升降温试验，模型的环境适应性有待考证，目前并没有应用于工程的报道。相比于国外同行，国内光纤陀螺温度漂移的研究较多地关注补偿算法本身，而在试验方法方面考虑欠缺，存在试验数量不足，测试时间较短等问题。这些是造成温补效果不理想，适应性较差的重要原因。

本文从试验设计与算法研究两方面入手。通过综合运用多种温度试验方法，控制误差轨线覆盖温度/温变速率平面，有效激励了全温范围内的零偏漂移特性。并利用非线性偏最小二乘辨识温度误差模型，在兼顾算法简便性的同时，获得了良好的拟合与预测效果和较高的温度环境适应性。

1 温度试验设计

1.1漂移模型项的选取

(1)

(2)

针对本惯导系统环境温度使用需求，在陀螺标度因数已预先经过温度补偿并忽略安装误差变化的条件下，以温箱开机显示温度作为起始温度，设计以下三组温箱升降温试验验证式(2)所选模型项的充分性：

第一组：起始保温4 h，-1 ℃/min降至0 ℃，低温保温2 h，+1 ℃/min升至40 ℃，高温保温2 h；

第二组：起始保温4 h，-1 ℃/min降至0 ℃，低温保温5 h，+1 ℃/min升至40 ℃，高温保温5 h；

第三组：起始保温1 h，-0.5 ℃/min降至0 ℃，低温保温2 h，+0.5 ℃/min升至40 ℃，高温保温4 h。

由于传感器位于陀螺壳体表面，其与光纤环温度存在差异，需要采取一定延时处理。以X方向陀螺为例，经过平滑的陀螺输出与对应变温速率如图1所示。可以看出，陀螺输出产生了与温变速率相关的漂移误差。当温变速率相同时(三角标示)，无论是升温(虚线)还是降温过程(点划线)，变温前是否处于稳态平衡(试验第一组与第二组)，温箱环境设定速率是否相同(试验第二组与第三组)，所对应的陀螺输出值几乎相同(方块标示)。说明在环境变温过程中，陀螺大致处于等温状态，空间温度梯度很小，温度高阶导数对漂移的影响可以忽略。

1.2温箱传递函数辨识与陀螺恒速率变温试验

由于零偏误差与温变速率高度相关，有必要单独研究陀螺本体以恒定温变速率通过不同温度点时的行为特征。这里首先通过阶跃响应辨识以温箱设定温度Tc为输入，陀螺测温传感器测量Tg为输出的传递函数。近似此过程为二阶系统，归一化的传递函数Gc写为

(3)

(4)

式中：L-1表示Laplace反变换，ΔTc为设定的阶跃温度差，Tc0为阶跃开始前温箱温度，ΔTg为温度稳态时由于元件发热导致的陀螺本体与温箱环境间的温差。通过安排如下试验，利用面积法进行辨识[19]：

从开机温度降至-20 ℃，充分保温7 h，正向以温箱最快速率升温至+50 ℃，保温7 h。

只采用正向快速升温是由于温箱的制热能力强于制冷能力，可以更好地模拟阶跃输入。试验获得的测温传感器温度响应及辨识效果如图2所示，辨识参数见表1。其中三只陀螺温度传感器测量值几乎重合，也进一步说明惯导内部温度分布具有很好的均匀性。

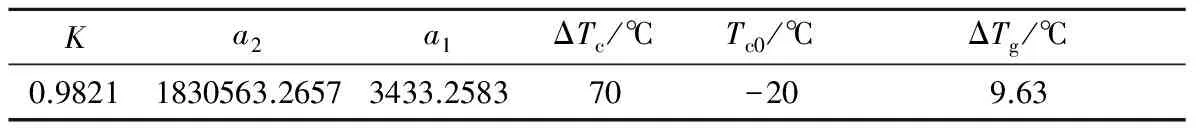
表1 参数辨识结果Table 1 Results of parameter identification

在此基础上，若希望陀螺本体以恒定速率变温，则需要反解传递函数以获得温箱控制输入。设期望恒定变温速率为λ，则温箱控制输入为

KI·I(t)+Kt·t+Tc0

(5)

式中：δ(t)为冲击函数，I(t)为单位阶跃函数。从而温箱控制输入应采取阶跃与斜坡函数的叠加。试验发现，在惯导技术指标要求所需的温度环境中，存在的陀螺本体最快温变速率约为8×10-3℃/s，大多在4×10-3℃/s以下，因此我们选择±4×10-3℃/s与±2×10-3℃/s两组典型速率进行试验，对应的温箱控制参数见表2。

表2 温箱控制参数Table 2 Control parameters of chamber

具体恒速率变温试验方法如下所示：

开机升温至25.4 ℃，对惯导充分保温至稳态(此步骤是为了从陀螺输出中分离漂移误差，见第1.3节)，再分别升降温至+40与-20 ℃进行充分保温达稳态，之后按照表2参数设置温箱控制曲线，并保证陀螺温度穿过指标所需的温度区间，完成±4×10-3℃/s与±2×10-3℃/s四组陀螺恒速率升降温试验。

图3是X陀螺恒速率变温段的试验结果。从图3可以看出，陀螺温度以预期斜率进行了变化，陀螺输出则产生了与之成比例的漂移。此过程中，对应同一条温变速率曲线，相应陀螺输出却出现了一定起伏，例如方块标示处呈现下降趋势，而对应同一升温或降温过程中不同温变速率的曲线，其出现位置处的绝对温度(19 ℃与23 ℃)基本相同。在温度一阶导数恒定，高阶导数为零的情况下，此现象只可能由绝对温度影响所致，其成因可能是由光纤环材料在不同温度处的应力改变引起[20]，说明零偏漂移不仅与温变速率有关还与绝对温度密切相关，这进一步证实了所选模型项的充分性。恒定速率升降温试验能够有效激励由温变速率引起的零偏漂移，并能够体现绝对温度的影响。作为下节中一类重要的特征轨线，该试验可以有效提高补偿模型的环境适应性与预测精度。

1.3温度/温变速率平面覆盖性试验

按照图4中参数设置温箱高低温循环完成漂移轨线覆盖试验，其中升降温速率均为±1 ℃/min。

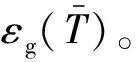
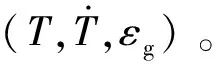
表3 轨线交点处零偏漂移值Table 3 Bias drift value at trajectory intersections

2 非线性零偏温度误差补偿方法

综合考虑温度与温变速率间各自独立与相互耦合作用，将式(2)分解为三种作用的组合。

(6)

其中，非线性项g1，g2，g3的辨识采用非线性偏最小二乘方法[21-22]。

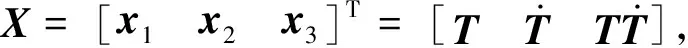
(7)

式中：定义结点ξj,l-1=min(xj)+(l-1)hj，hj=(max(xj)-min(xj))/Mj，区间分段数Mj可根据拟合效果选定。式(7)中样条基函数ΩΚ的表达式为

(8)

(9)

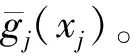
(10)

从而零偏漂移的估计形式为

(11)

第二部分就是利用偏最小二乘计算回归系数β0与βj,l。偏最小二乘方法借鉴了主成分回归的思想，能够提取与因变量最相关的成分参与建模而达到很高的拟合质量，同时避免式(11)中基向量较多所产生的多重共线性。具体步骤可归纳如下：

步骤1.记样条基集合Zj=(zj,0,zj,1,…,zj,Mj+K-1)，则集合全体Z=[Z1Z2Z3]，零漂观测集合为εg。再将两者标准化为Z0与εg0(样本均值为0，方差为1)。

(12)

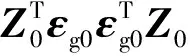
步骤3. 求解ω1，可得主成分t1=Z0ω1。之后分别将Z0和εg0对t1做线性回归，即

(13)

式中：p1，q1为回归系数。Z1，εg1为残差矩阵。

步骤4.利用残差Z1，εg1代替Z0和εg0，按照步骤2求第二主轴ω2，得到第二主成分t2。继续用Z1和εg1对t2做回归，得到p2，q2，Z2，εg2，即

(14)

如此计算下去，最后若Z的秩为A，则有

(15)

由于t1,t2,…,tA均可表示为Z0的线性组合，从而式(15)可还原为εg0对Z0的回归方程形式。

(16)

(17)

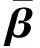
3 补偿效果验证

3.1模型辨识效果

利用图6中轨线数据集所获得的零漂与对应温度状态建立误差模型并进行补偿。根据拟合质量，每轴陀螺均选取多项式阶数K=3，分段数Mj=5。图7是温度循环试验(图4)补偿前后的陀螺输出对比。由于结合了基函数非线性描述能力与提取观测与状态间最相关的成分参与建模，辨识模型达到了很高的精度而使补偿之后的输出几乎不再受到温度变化的影响。两者的100 s标准差(1σ)见表4，补偿后的陀螺零偏稳定性已小于0.005°/h。

表4 温度循环试验补偿前后陀螺输出标准差对比Table 4 Comparison of standard deviation of gyro output before and after compensation in temperature cycle experiment

3.2模型环境适应性

为了充分检验温度模型环境适应性，首先采用两组全温范围内温箱随机变温试验进行验证，整个过程中不让惯导经历温度稳态过程，且采用不同升降温速率。试验结果如图9所示。

可见即使温度存在无规则大范围剧烈波动，惯导陀螺输出依然非常平稳，100 s统计结果也验证了这一点(见表5),并且各次试验都取得了一致的补偿效果，三方向陀螺稳定性由0.02°/h水平降至0.005°/h以下。

表5 随机温变试验补偿前后陀螺输出标准差对比Table 5 Comparison of standard deviation of gyro output before and after compensation in random temperature variation experiment

由于温箱环境与导航系统工作环境存在差异，因此进一步利用实际的惯导工作过程对补偿模型进行检验。图10是静态惯导冷启动4 h的补偿效果，相应标准差列于表6。可见补偿效果同样良好，实时导航结果如图11所示(对准时间30 min)，经零位温度补偿后，导航误差中舒拉振荡分量的幅值与随时间线性增长分量的斜率都已明显减小，1 h导航误差的最大值由1516 m减小为594 m。

表6 冷启动过程补偿前后陀螺输出标准差对比Table 6 Comparison of standard deviation of gyro output before and after compensation during cold boot process

4 结 论

光纤陀螺零偏温度误差模型的环境适应性是惯导系统实际使用精度提高的一个难点。本文从试验和算法两方面对此开展研究。设计相关验证试验确定了非线性模型项组成。通过反向利用温箱传递函数，获得了陀螺以受控温变速率通过各温度点的漂移特征，并与误差轨线循环试验相结合，将温度环境适应性问题转化为零漂对温度/温变速率平面的覆盖性问题。在试验数据集基础上，利用非线性偏最小二乘法辨识了零偏温度误差模型并揭示了温度状态在漂移形成中的组成形式与所起作用。通过随机变温与惯导冷启动工作过程充分检验了补偿模型的适应性，零偏稳定性与导航精度都得到了显著提高。本方法具有较高的工程实用价值，也可推广至激光陀螺，以及其它类型具有相似行为传感器的温度误差补偿之中。

[1] Vali V, Shorthill R W. Fiber ring interferometer[J]. Applied Optics, 1976, 15: 1099-1100.

[2] Barbour N, Schmidt G. Inertial sensor technology trends[J]. IEEE sensors journal, 2001, 1(4): 332-339.

[3] Lefevre H C. The fiber-optic gyroscope, a century after Sagnac′s experiment: the ultimate rotation-sensing technology[J]. C. R. Physique, 2014, 15: 851-858.

[4] Dzhashitov V E, Pankratov V M. Using the method of elementary balances for analysis and synthesis of thermal control system for FOG SINS based on peltier modules[J]. Gyroscopy and Navigation, 2014, 5(4): 245-256.

[5] 孟照魁, 崔佳涛, 章博, 等. 高精度光纤陀螺温度实验研究[J]. 宇航学报, 2007, 28(3): 580-583. [Meng Zhao-kui, Cui Jia-tao, Zhang Bo, et al. Experiment research of the high precision optical fiber gyroscope temperature[J]. Journal of Astronautics, 2007, 28(3): 580-583.]

[6] Liu R Y, El-Wailly T F, Dankwort R C. Test results of Honeywell′s first generation, high-performance interferometric fiber-optic gyroscope[C]. Proc. SPIE 1585, Boston, US, September 3, 1991.

[7] Cordova A, Patterson R, Rahn J, et al. Progress in navigation grade IFOG performance[C]. Proc. SPIE 2837, Denvor, US, August 4, 1996.

[8] 金靖, 王峥, 张忠钢, 等. 基于多元线性回归模型的光纤陀螺温度误差建模[J]. 宇航学报, 2008, 29(6): 1912-1916. [Jin Jing, Wang Zheng, Zhang Zhong-gang, et al. Temperature errors modeling for fiber optic gyroscope using multiple linear regression models[J]. Journal of Astronautics, 2008, 29(6): 1912-1916.]

[9] Dzhashitov V E, Pankratov V M, Golikov A V, et al. Hierarchical thermal models of FOG-based strapdown inertial navigation system[J]. Gyroscopy and Navigation, 2014, 5(3): 162-173.

[10] Dranitsyna E V, Egorov D A, Untilov A A, et al. Reducing the effect of temperature variations on FOG output signal[J]. Gyroscopy and Navigation, 2013, 4(2): 92-98.

[11] Benini A, Senatore R, D′Angelo F, et al. A closed-loop procedure for the modeling and tuning of Kalman filter for FOG INS[C]. Inertial Sensors and Systems Symposium, Karlsruhe, Germany, September 22-23, 2015.

[12] 张潇, 卓超. 基于分类建模的光纤陀螺温度效应补偿方法[J]. 航天控制, 2016, 34(3): 36-40. [Zhang Xiao, Zhuo Chao. A compensation method for FOG temperature effect error based on modeling of classified data[J]. Aerospace Control, 2016, 34(3): 36-40.]

[13] 冯丽爽, 南书志, 金靖. 光纤陀螺温度建模及补偿技术研究[J]. 宇航学报, 2006, 27(5): 939-941. [Feng Li-shuang, Nan Shu-zhi, Jin Jing. Research on modeling and compensation technology for temperature errors of FOG[J]. Journal of Astronautics, 2006, 27(5): 939-941.]

[14] Zhang Y, Wang Y, Yang T, et al. Dynamic angular velocity modeling and error compensation of one-fiber fiber optic gyroscope (OFFOG) in the whole temperature range[J]. Measurement Science and Technology, 2012, 23(2): 1-6.

[15] 王威, 陈熙源. 一种基于多尺度和改进支持向量机的光纤陀螺温度漂移建模与补偿方法[J]. 中国惯性技术学报, 2016, 24(6): 793-797. [Wang Wei, Chen Xi-yuan. Modeling and compensation method of FOG temperature drift based on multi-scale and improved support vector machine[J]. Journal of Chinese Inertial Technology, 2016, 24(6): 793-797.]

[16] Lefevre H C. The fiber-optic gyroscope (2nd Ed.)[M]. Boston and London: Artech House, 2014.

[17] Mohr F. Thermooptically induced bias drift in fiber optical Sagnac interferometers[J]. Journal of Lightwave Technology, 1996, 14(1): 27-41.

[18] Mohr F, Schadt F. Rigorous treatment of fiber-environmental interactions in fiber gyroscopes[C]. IEEE International Conference on Computational Technologies in Electrical and Electronics Engineering, Novosibirsk, Russia, July 21-25, 2008.

[19] 萧德云. 系统辨识理论及应用[M]. 北京: 清华大学出版社, 2014.

[20] Mohr F, Schadt F. Error signal formation in FOGs through thermal and elastooptical environment influences on the sensing coil[C]. Inetial Sensors and Systems Symposium, Karlsruhe, Germany, September 2011.

[21] 王惠文, 吴载斌, 孟洁. 偏最小二乘回归的线性与非线性方法[M]. 北京: 国防工业出版社, 2006.

[22] Word H. Partial least squares[M]. New York: John Wiley & Sons, 1985.

AHighlyAdaptiveCompensationMethodforNonlinearThermalBiasErrorofFiber-OpticGyroscopes

ZHUO Chao1,2, DU Jian-bang1,2

(1. Beijing Aerospace Automatic Control Institute, Beijing 100854, China; 2. National Key Laboratory of Science and Technology on Aerospace Intelligent Control, Beijing 100854, China)

The composition of the thermal bias error of fiber-optic gyroscopes is determined and a series of temperature experiments are designed to validate the adequacy of the selected modeling terms. The inverse solution of the chamber transfer function is obtained to realize the control of the chamber input and manipulate the body temperature of the gyroscopes to change at the constant rates. Combining this invariant rate changing experiment with the thermal cycle in different temperature zones, the error trajectory is directed to cover the temperature/temperature derivative plane which illustrates the dependence relation between the plane coverage and the environment adaptability. The nonlinear thermal drift model is accurately identified by means of the nonlinear partial least square estimation. Also the form and the contribution of each temperature component leading to the drift are acquired simultaneously. Both the random thermal variation and SINS cold boot experiments demonstrate the high adaptability of the proposed method to the complex temperature environment. After the thermal compensation, the gyro bias stability in full temperature range is reduced from the level of 0.02°/h to better than 0.005°/h.

Fiber-optic gyroscope; Thermal bias error; Temperature experiment design; Nonlinear partial least square

U666.1

A

1000-1328(2017)10- 1079- 09

10.3873/j.issn.1000-1328.2017.10.008

2017- 06- 19;

2017- 07- 27

国家自然科学基金(61603365)

卓超(1988-)，男，博士生，主要从事导航、制导与控制方面研究。

通信地址：北京市海淀区永定路52号(100854)

电话：(010)88526662

E-mail:ngjyzc@126.com