临近空间高超声速目标修正随机Hough变换TBD算法

李岳峰，王国宏，李 林，张翔宇

(海军航空工程学院信息融合研究所，烟台 264001)

临近空间高超声速目标修正随机Hough变换TBD算法

李岳峰，王国宏，李 林，张翔宇

(海军航空工程学院信息融合研究所，烟台 264001)

针对临近空间高超声速目标的检测跟踪问题，提出一种修正的随机Hough变换检测前跟踪算法。首先，为尽可能克服远距离条件下角度误差带来的较大位置偏差，通过解耦的方式将量测点迹映射至精度较高的径向距离-时间平面进行检测；然后，为更合理地合并参数空间特征点并提升积累效率，构建检验统计量并与自适应门限进行比较，将特征点合并问题转换成两个正态总体均值差的自适应假设检验问题，并利用点数积累与能量积累相结合的双重积累方式进行积累检测；最后，为进一步降低虚假航迹数，引入运动约束和航迹合并措施，得到最终按时序关联的检测航迹。仿真结果表明，相比标准Hough变换检测前跟踪算法，本文算法在检测概率相差不大的情况下具有更少虚假航迹和更低运行时间。

临近空间；高超声速目标；检测前跟踪；随机Hough变换；特征点合并

0 引 言

临近空间是指距地面20～100公里的空域，处于现有飞机的最高飞行高度和卫星的最低轨道高度之间，由于其重要的开发应用价值而引起广泛关注。临近空间高超声速飞行器是以不低于5马赫的速度在临近空间执行任务的一类飞行器，可以在2小时内对全球任一目标执行快速精确打击，给我国空天安全体系造成巨大威胁[1-4]。因此，临近空间高超声速飞行器的检测跟踪技术研究对增强国家空天安全具有重要意义。

检测前跟踪(Track-before-detect, TBD)技术是一种强杂波环境下检测微弱目标的有效方法[5-8]。TBD采用批处理的思想，对多帧采样数据进行非相参积累，提高了目标航迹信噪比(Signal-noise ratio, SNR)，在检测出目标点迹的同时可以起始目标航迹。基于Hough变换的TBD算法(Hough transform track-before-detect, HT-TBD)具有对随机噪声鲁棒性强、对目标位置不确定性及局部缺损不敏感等优点，在雷达探测领域应用广泛[9-13]，但在强杂波环境下仍存在计算量大、占据存储空间多和运行用时长的缺点，不利用航迹的快速起始。

文献[14]首次提出随机Hough变换的方法，该方法利用多对一映射的思想，采取随机抽样、收敛映射和动态链表的方式进行数据空间到参数空间的映射，避免了标准Hough变换在无用区间的大量无效积累，运算速度显著提高，并且具有参数空间无限大、参数精度无限高等优点；文献[15]基于三维直线的Roberts表示法，提出一种相似性判决的方法，实现了较低采样次数下的相似Roberts参数合并；文献[16]针对标准HT-TBD算法在低信噪比环境下检测概率较低和运算时间较长的问题，提出一种基于遍历随机Hough变换的TBD方法，将数据点两两遍历组合后进行多对一映射，可以在保证检测概率的同时缩短运算时间；文献[17]通过方位变换的方式将机动弱目标解距离模糊的问题转换为TBD框架下的基于随机Hough变换的航迹检测问题，避免了低信噪比条件下微弱目标的航迹漏检。但是对于远距离的临近空间高超声速目标，即使雷达角度测量误差很小，也会产生高达若干公里的横向偏差，如何尽可能地克服较大位置偏差并快速完成航迹检测跟踪仍是一个未解决好的问题。

针对上述问题，本文提出一种临近空间高超声速目标修正随机Hough变换TBD算法。该算法通过解耦的方式选取径向距离-时间量测数据进行修正随机Hough变换；然后，基于参数空间特征点分布误差分析，在文献[11]的基础上，提出一种基于自适应假设检验的特征点合并方法，有效减小了因选取固定合并门限而造成的检测性能损失；其次，对合并后特征点采用点数积累与能量积累相结合的双重积累方式进一步提升积累效率；最后，分别借鉴文献[10,18]思想，利用运动约束和航迹合并进一步精简航迹，最终有效实现了远距离强杂波条件下临近空间目标的快速检测跟踪。

1 问题描述

1.1目标量测模型

假设二坐标雷达位于坐标原点，雷达扫描周期为T，批处理回波信号数为N帧，则k时刻临近空间点目标状态向量：

Xk=[Rk,ψk,Sk]T

(1)

式中：Rk,ψk分别为k时刻目标的径向距离与方位角，Sk为目标回波功率值，则量测方程可表示如下：

Zk=HXk+Wk

(2)

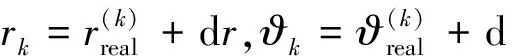
(3)

式中：Nk(rk,ϑk)表示k时刻(rk,ϑk)点处零均值高斯白噪声的功率值，Sk(rk,ϑk)表示k时刻(rk,ϑk)点所对应目标点的功率值，根据雷达方程[19]：

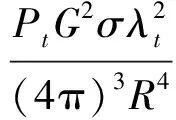
(4)

式中：Pt为发射功率，G为发射增益，σ为目标散射截面积，λt为发射波长，R为径向距离。

1.2算法总体流程

本文算法从总体结构上可以分为三部分：径向距离-时间平面的随机Hough变换、基于自适应假设检验的特征点合并与双重积累以及航迹检验与合并，具体算法流程如图1所示。

2 算法原理

2.1径向距离-时间平面的随机Hough变换

针对强杂波背景下原始数据处理量大的问题，本文在较高虚警率下设置较低的第一门限，可以在保留原始目标点的同时滤除部分杂波点，从而达到减少计算量的目的。根据预设的虚警概率Pfa，对于经过平方率检波的回波信号，第一门限h可取：

h=-ln(Pfa)

(5)

为预留足够预警时间，对临近空间高超声速目标进行探测时目标距离雷达往往很远，此时即使雷达角度测量误差很小，也会产生高达若干公里的横向偏差。因此，远距离条件下距离量测与角度量测耦合而产生的较大横向偏差将使得通常情况下采用x-y直角坐标位置量测进行随机Hough变换的处理方式难以实现对临近空间高超声速目标的有效检测跟踪。考虑到雷达测距误差只有几百米，精度较高，因此本文采用解耦的方式，选取径向距离-时间量测数据进行随机Hough变换，在引入时序信息的同时，有效避免了角度误差对随机Hough变换积累检测的消极影响，方位角量测通过后续角度约束的引入得以利用，从而保证了算法信息利用率。

考虑到映射后径向距离-时间平面的坐标轴量级相差较大，直接进行随机Hough变换将因量级较小的时间轴信息的损失而难以进行峰值检测，因此本文对于径向距离-时间数据进行规格化预处理[20]，规格化系数c可以设置如下：

(6)

式中：「lg(|rmax/tmax|)⎤表示大于等于lg(|rmax/tmax|)的最小整数，rmax表示径向距离r的最大值，tmax表示积累时帧数t的最大值。经过规格化处理，量测数据由(t,r)变换为(t′,r′)=(c×t,r)。

在规格化预处理的基础上，本文选用径向距离-时间数据按照式(7)进行随机Hough变换：

ρ=t′cosθ+r′sinθ

(7)

式中：ρ为量测点所在直线与原点的垂线距离，θ为该垂线与横轴正方向的夹角。

根据随机Hough变换理论，共线数据点对应参数空间的一个特征点。由于两点确定一条直线，因此可以通过随机抽取两个数据点而映射得到参数空间对应直线的特征点。假设r-t平面内随机抽取的两点分别为(t1,r1)和(t2,r2)，代入式(7)可得：

(8)

求解可得对应直线的参数空间特征点(ρ0,θ0)：

(9)

为了避免不合理的点对选取方式而造成的错误积累和计算资源的浪费，采样点对的选取遵循以下两项原则：

1)为了避免在单帧量测数据中检测到目标航迹的不合理情况，根据时间序列仅仅处理拥有不同时戳信息的随机采样数据点对；

2)对于随机采样数据点对引入速度粗关联，利用速度先验信息仅仅处理平均速度v0介于目标最小速度vmin和最大速度vmax之间的数据点对：

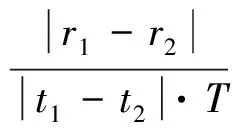
(10)

2.2基于自适应假设检验的特征点合并与双重积累

由于量测误差的存在，直线运动的目标量测点迹不会严格处于一条直线。因此，任意目标点对所对应的特征点也不会完全重合于一点，而是随机分布在真实目标特征点附近。为了后续更合理地合并邻近的特征点，下面对参数空间特征点分布进行误差分析。

假设r-t平面内随机抽取的两点分别为(t1,r1)和(t2,r2)，对应的距离量测误差分别为dr1和dr2，由于时间量测数据无误差，则dt1=dt2=0。

根据式(9)，对θ0求全微分可得

(11)

根据式(9)，对ρ0求全微分可得：

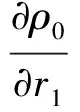
sinθ0dr1+(r1cosθ0-ct1sinθ0)dθ0

(12)

(13)

参数空间特征点的合并是随机Hough变换的一个关键问题，合并准则选取的合理与否直接影响着参数空间的积累效率与峰值提取后的算法检测概率。现有研究往往根据经验选取固定的合并门限η从而造成较大检测性能损失，本文提出一种自适应假设检验的方法，利用不断更新的检验统计量与动态变化的合并门限进行比较，从而对参数空间特征点进行更为合理的合并；同时，对于合并后特征点采用点数积累与能量积累相结合的双重积累方式进一步提升积累效率，从而可在充分利用点迹能量信息的同时减小强干扰影响，避免单一积累方式的明显缺陷。

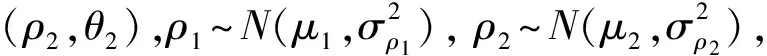
(14)

在置信度为(1-α)的条件下，检验统计量Tρ服从自由度为(n1+n2-2)的T分布：

(15)

(16)

在置信度为(1-α)的条件下，检验统计量Tθ服从自由度为(n1+n2-2)的T分布：

(17)

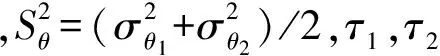
为了在减小无效积累次数的同时尽可能降低积累参数偏差，本文算法采取如下三种改进措施：

1)如果出现某一特征点与已存储的多个特征点均可合并的情况，则该特征点只与已存储的欧氏距离最小的特征点进行合并；

2)为了减小初始存储特征点可能存在的较大偏差，采用等权重迭代平均的方式更新合并后的特征点参数：

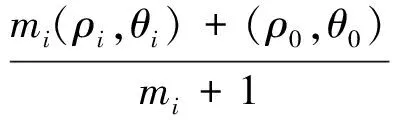
(18)

其中，(ρ0,θ0)为新输入的特征点样本，(ρi,θi)为已存储的第i个积累特征点，mi为其对应的数据点积累个数，i=1,2,…,Q，Q为已存储的特征点总数。随着采样点对数的不断增加，直线参数会持续更新并逐渐接近真实直线参数。

3)由于数据点对是随机采样的，可能存在同一数据点为某一已存特征点多次重复投票的虚假积累情况。因此，本文算法建立投票点积累矩阵记录给各个特征点投票的数据点，并将每一特征点的互异投票数据点数作为其最终的数据点个数积累值。

在特征点合并的基础上，本文采用点数积累与能量积累相结合的双重积累方式进一步提升参数空间特征点积累效率，考虑到实际问题中单帧数据中只存在一个目标点迹，为了避免大量杂波点的无效积累湮没真实目标航迹积累值，按照下述两项原则进行更为合理的双重积累：

1)对于二值积累，同一时刻任意特征点至多积累一票，即若无其他特征点与其合并，记0票；如果存在大于或等于一个特征点可与其合并，记1票；

2)对于非相参积累，同一时刻任意特征点只积累所有投票数据点中功率最大点的功率值；若没有点迹为该特征点投票，此时刻该特征点的功率积累值记为零。

2.3航迹检验与合并

为进一步去除逆映射后按时序关联的不满足临近空间高超声速目标运动规律的虚假航迹，本文算法引入航迹速度、角度和加速度约束进行航迹检验。

假设逆映射后检测出的任意三个时刻ti,tj,tk的量测向量分别为Zi=[ri,ϑi,Ei]T,Zj=[rj,ϑj,Ej]Τ以及Zk=[rk,ϑk,Ek]T，对应的距离向量分别为bij=Ζi-Ζj,bjk=Ζj-Ζk，其中，i,j,k=1,2,…,N，i≤j≤k。具体的运动约束条件如下

(19)

式中：|·|表示取模运算，vmax、vmin分别为先验速度最大值和最小值，βmax、amax分别为先验的目标最大转向角和最大加速度。

针对航迹检验后可能存在的多条检测航迹对应同一目标的航迹簇拥现象，本文算法进一步进行航迹合并。若两条可能航迹的公共点个数超过门限δ0，则合并这两条航迹，合并门限δ0可表示如下：

(20)

3 修正随机Hough变换TBD算法实现

对于雷达接收到的原始量测数据，本文修正随机Hough变换TBD算法的具体实现步骤如下：

步骤2.量测数据预处理。根据预设虚警概率Pfa，利用式(5)设置第一门限h；利用式(6)计算规格化系数c，对映射至径向距离-时间平面的量测数据进行规格化处理，量测变换为(t′,r′)=(c×t,r)；

步骤3.随机抽取数据点对。从N帧数据中随机抽取具有不同时戳的数据点对，并根据式(10)计算两点间的平均速度v0，如果v0处于先验的速度区间[vmin,vmax]，转至步骤4；否则，执行步骤6；

步骤4.特征点分布误差分析。对于随机点对对应的特征点(ρ0,θ0)进行误差分析，根据式(13)计算出误差dρ0、dθ0的分布；

步骤5.特征点合并与双重积累。搜索动态链接列表L中已保存的特征点，并根据式(15)和式(17)构建假设检验统计量Tρ和Tθ，找出使二者均满足自适应合并门限(即同时使各自原假设H0成立)的已存特征点集合Α；

如果A≠∅，搜索与(ρ0,θ0)欧氏距离最近的特征点(ρi,θi)进行合并，同时进行点数积累与能量积累，然后，更新矩阵F1和F2，并将投票数据点存入矩阵R。此外，利用式(19)对合并后的特征点参数进行更新并对其投票点进行去重，根据去重后的投票点记录矩阵R对矩阵F1和F2进行更新，得到最终的点数与能量积累值。

如果A=∅，动态链接列表L中不存在相匹配的特征点，则将(ρ0,θ0)插入到列表L中，并在矩阵F1、F2和R中建立相应单元用于分别存储其对应的投票点数、能量积累值以及投票数据点。

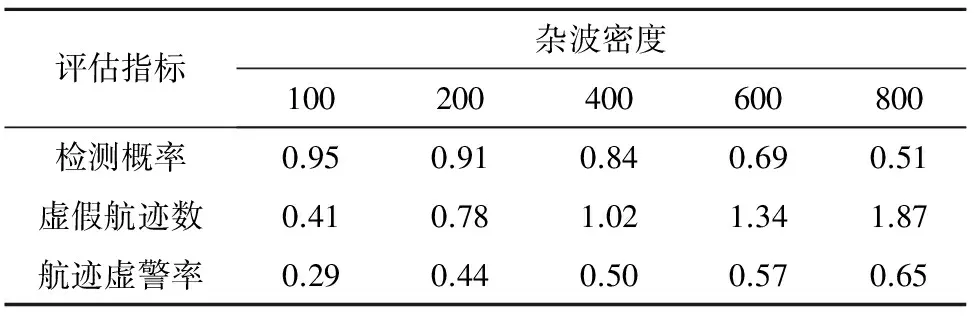
步骤6.令采样次数计数变量s=s+1。此时，如果s

步骤7.峰值提取与逆映射。遍历动态链接列表，对于点数积累值超过门限ξ1且能量积累值超过门限ξ2的特征点进行逆映射，并通过时序关联得到可能航迹；

步骤8.航迹检验。根据式(19)对可能航迹进行速度、角度和加速度约束，删除不满足运动规律的航迹；

步骤9.航迹合并。对满足运动约束的可能航迹进行两两比较，并对公共点个数超过式(20)中门限δ0的航迹进行合并。最后，将航迹合并后的结果输出，作为最终检测航迹。

4 仿真验证与分析

4.1参数设置

假设二坐标雷达位于坐标原点，扫描周期T=1 s，批处理回波信号帧数N=7，测距误差为400 m，测角误差为0.2°。在每帧数据中杂波个数服从泊松分布，杂波位置服从均匀分布，杂波密度为λc，目标的散射截面积为2 m2。特征点合并置信度为0.95，点数积累门限值ξ1=4，能量积累门限值ξ2为参数空间能量积累最大值的0.85倍。预设先验最小速度vmin=Ma5，最大速度vmax=Ma20，最大转向角βmax=80°，最大加速度amax=15g，其中，g= 9.8 m/s2。约束因子τ=1，航迹合并门限δ0=4。假设临近空间高超声速目标做匀加速直线运动，初始位置为(350 km,350 km)，即位置量测向量(r,ϑ)=(494.97 km,45°)，初始速度为(3000 m/s,2000 m/s)，初始加速度为(60 m/s2,40 m/s2)。

4.2算法有效性验证

为验证算法有效性，针对上述参数设置，在信噪比等于6 dB、杂波密度λc=300的条件下进行仿真试验。叠加后的7帧量测数据点分布以及数据预处理后经过映射的径向距离-时间平面量测数据点分布依次分别如图2(a)和图2(b)所示。由于量测误差的引入，目标量测点已不完全处于标准直线，而是随机分布于真实航迹附近，线性弱化的目标航迹增大了检测的难度。

对于预处理后径向距离-时间平面的映射点迹，根据第2.2节基于自适应假设检验的特征点合并与双重积累的实施步骤与执行原则，可以得到参数空间的点数积累和能量积累的三维杆状图，依次分别如图3(a)和图3(b)所示。由图3可知，随机Hough变换利用随机采样的思想，通过较少次数的多对一映射得到了不存在峰值模糊的参数空间积累图，较为明显的特征点积累峰值证明了检测的可行性。

在特征点合并与双重积累的基础上，对于点数积累值超过门限ξ1且能量积累值超过门限ξ2的特征点进行逆映射，如图4(a)所示。此时算法在检测到目标量测点的同时还会检测到一定量杂波点，为进一步去除杂波点并得到按时序关联的检测航迹，根据第2.3节引入目标运动约束并进行航迹合并，得到如图4(b)所示的最终检测航迹。通过与真实目标量测点的对比可知，不符合运动规律的虚假航迹与重复航迹得以进一步去除，算法可以在检测到大部分目标量测点的同时尽可能地抑制杂波，从而有效地回溯航迹。

4.3不同信噪比对算法性能的影响

为进一步验证信噪比对于本文算法检测性能的影响，在上述参数设置下针对不同信噪比各进行500次Monte Carlo仿真试验，本文算法的检测性能如表1所示。

由表1可知，本文算法的检测概率随信噪比的增加而升高，虚假航迹数和航迹虚警概率均随信噪比的增加而降低。当信噪比大于等于6 dB时，检测概率较高，可达90%以上，航迹虚警率也在50%以下；随着信噪比的降低，过门限噪声和杂波点逐渐增多，检测性能存在较为明显的下降(尤其在4 dB附近)，当信噪比小于等于2 dB时，检测概率低于20%，同时，航迹虚警率也达到65%以上。

表1 不同信噪比条件下的算法性能Table 1 Algorithm performance under different SNR

4.4不同杂波密度对算法性能的影响

为进一步验证杂波密度对于本文算法检测性能的影响，在上述参数设置下针对不同杂波密度各进行500次Monte Carlo仿真试验，本文算法的检测性能如表2所示。

表2 不同杂波密度条件下的算法性能Table 2 Algorithm performance under different clutter density

由表2可知，本文算法的检测概率随杂波密度的增加而降低，同时，对应的虚假航迹数和航迹虚警概率均随杂波密度的增加而升高。当杂波密度小于等于200时，检测概率可达90%以上，对应的航迹虚警率也保持在45%以下；随着杂波密度的增加，所处理量测点中干扰杂波的比例越来越大，抽取到杂波点对从而在参数空间进行无效积累的可能性也越来越大，此时，检测性能存在较为明显的降低，并随着杂波密度的增加而愈发明显；当杂波密度大于800时，检测概率会开始低于50%，航迹虚警率也达到65%以上。由于径向距离-时间平面内基于自适应假设检验特征点合并的修正随机Hough变换已筛选掉大部分干扰点迹，后续引入的航迹约束和航迹合并又进一步去除了部分虚假航迹，因此，本文算法具有较低的虚假航迹数。

4.5算法性能比较

为进一步验证算法性能，在上述参数设置下针对信噪比分别等于0 dB, 2 dB, 4 dB, 6 dB, 8 dB, 10 dB, 20 dB, 40 dB, 80 dB, 100 dB, 200 dB的仿真条件对本文算法和标准Hough变换算法各进行500次Monte Carlo仿真试验，两种算法检测性能对比如表3所示。

表3 两种算法检测性能对比Table 3 Detection performance comparison of two algorithms

从表3可以看出：

1) 两种算法的检测概率均随信噪比的增加而升高，标准Hough变换算法的检测概率整体上高于本文算法，但二者相差不大。本文算法将量测点映射至径向距离-时间平面进行修正随机Hough变换，有效避免了远距离条件下角度误差对随机Hough变换积累检测的消极影响；基于特征点误差分析，本文提出一种自适应假设检验特征点合并方式，避免了根据经验选取固定合并门限造成的较大检测性能损失；点数积累与能量积累相结合的双重积累方式使参数空间积累效率进一步提升。基于上述三点原因，尽管采用基于有限次随机采样的随机Hough变换，本文算法的检测概率仍与标准Hough变换算法相差不大。当信噪比小于4 dB时，随着信噪比的降低，过初始门限的干扰点明显增多，两种算法的检测概率下降较为明显；当信噪比大于6 dB时，两种算法的检测概率均在90%以上，可以对临近空间高超声速目标进行有效检测；当信噪比大于20 dB时，目标相对噪声已经非常明显，两种算法的检测概率均接近于1。由于本文进行的是有限次Monte Carlo仿真试验，因此当信噪比很大时会出现试验的检测概率等于1的情况。

2) 两种算法的虚假航迹数和航迹虚警概率均随信噪比的增加而降低，并且同等条件下本文算法的虚假航迹明显少于标准Hough变换算法。自适应假设检验的特征点合并方式提升了传统固定合并门限方式的准确性，有效减少了目标点与干扰点的错误合并；引入的航迹检验与航迹合并措施进一步减少了算法的虚假航迹。因此，与标准Hough变换算法相比，本文算法具有明显更少的虚假航迹。当信噪比小于4 dB时，过初始门限的干扰点随信噪比的降低而明显增多，两种算法的虚假航迹存在较为明显的增加；当信噪比等于10 dB时，本文算法航迹虚警概率仅为标准Hough变换算法的42%；随着信噪比继续增大，目标点相对干扰点的区分度日益增加，两种算法的虚假航迹数逐渐趋近于0。由于本文进行的是有限次Monte Carlo仿真试验，因此当信噪比很大时会出现试验的虚假航迹数等于0的情况。

3) 两种算法的平均运行时间均随信噪比的增加而降低，并且同等条件下本文算法的平均运行时间明显低于标准Hough变换算法。由于初始门限预处理后过门限量测点的数量与信噪比的大小呈反比，因此在相同虚警概率下，信噪比越高，预处理后待检测量测点越少，平均运行时间也越低。由于利用了随机Hough变换数据点采样的思想，本文算法避免了标准Hough变换一对多的复杂映射和相应的大量无用参数区域的计算与积累，运算时间产生了量级上的减小，运算效率具有较为明显的提升。以信噪比为6 dB为例，此时本文算法的运算时间仅为标准Hough变换算法运算时间的7.4%。

5 结 论

本文针对临近空间高超声速目标的检测跟踪问题，提出一种在径向距离-时间平面内进行检测的修正随机Hough变换TBD算法。在特征点分布误差分析的基础上，通过自适应更新合并门限值的基于假设检验的特征点合并和点数积累与能量积累相结合的双重积累的改进措施，参数空间积累效率得以提升；采样点对选取方式和合并特征点参数更新方式等方面的改进在减小无效积累次数的同时也降低了积累参数偏差；多条件运动约束和航迹合并措施进一步精简了检测航迹。与标准HT-TBD算法相比，二者检测概率相差不大且本文算法在虚假航迹数和运行时间方面性能更优，具有一定工程实践意义。

[1] Zhang J M, Sun C Y, Zhang R M, et al. Adaptive sliding mode control for re-entry attitude of near space hypersonic vehicle based on backstepping design[J]. IEEE/CAA Journal of Automatica Sinica, 2015, 2(1): 94-101.

[2] Wang W Q. Near-space vehicle-borne SAR with reflector Antenna for high-resolution and wide-swath remote sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(2): 338-348.

[3] 黄伟, 罗世彬, 王振国. 临近空间高超声速飞行器关键技术及展望[J]. 宇航学报, 2010, 31(5): 1259-1265. [Huang Wei, Luo Shi-bin, Wang Zhen-guo. Key techniques and prospect of near-space hypersonic vehicle[J]. Journal of Astronautics, 2010, 31(5): 1259- 1265.]

[4] 张翔宇, 王国宏, 宋振宇, 等. LFM雷达对临近空间高超声速目标的跟踪研究[J]. 电子学报, 2016, 44(4): 846-853. [Zhang Xiang-yu, Wang Guo-hong, Song Zhen-yu, et al. Tracking of hypersonic target in near-space with LFM radar[J]. Acta Electronica Sinica, 2016, 44(4): 846-853.]

[5] 李林, 王国宏, 于洪波, 等. 一种临近空间高超声速目标检测前跟踪算法[J]. 宇航学报, 2017, 38(4): 420-427. [Li Lin, Wang Guo-hong, Yu Hong-bo, et al. A TBD algorithm for near space hypersonic target[J]. Journal of Astronautics, 2017, 38(4): 420-427.]

[6] Tang X, Ratnasingham T, Michael M, et al. Multiple detection-aided low-observable track initialization using ML-PDA[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(2): 722-735.

[7] Jiang H C, Yi W, Thia K, et al. Multi-frame radar detection of fluctuating targets using phase information[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(2): 736-749.

[8] Luis U M, Angel G F, Jesus G L. Adaptive auxiliary particle filter for track-before-detect with multiple targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 32(2): 1-24.

[9] Moyer L R, Spak J, Lamanna P. A multidimensional Hough transform based track-before-detect technique for detecting weak targets in strong clutter backgrounds[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 3062-3068.

[10] 王国宏, 李林, 于洪波. 基于点集合并的修正Hough变换TBD算法[J]. 航空学报, 2017, 38(1): 203-213. [Wang Guo-hong, Li Lin, Yu Hong-bo. A modified Hough transform TBD algorithm based on point set merging[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 203-213.]

[11] 吴泽民, 任姝婕, 倪明放. 基于修正随机Hough变换的快速航迹起始研究[J]. 系统仿真学报, 2009, 21(5): 1447-1450. [Wu Ze-min, Ren Shu-jie, Ni Ming-fang. Research of fast track initialization based on modified random Hough transform[J]. Journal of System Simulation, 2009, 21(5): 1447-1450.]

[12] 王国宏, 李林, 张翔宇, 等. 临近空间高超声速目标RHT-TBD算法[J]. 电光与控制, 2016, 23(9): 1-6. [Wang Guo-hong, Li Lin, Zhang Xiang-yu, et al. A RHT-TBD algorithm for near space hypersonic target[J]. Electronics Optics & Control, 2016, 23(9): 1-6.]

[13] Yu H, Wang G H, Wu W, et al. A novel RHT-TBD approach for weak targets in HPRF radar[J]. Science China Information Series, 2016, 59(12): 1-14.

[14] Kultanen P, Xu L, Oja E. Randomized Hough transform (RHT)[C]. The 10th International Conference on Pattern Recognition, Atlantic City, USA, June 16-21, 1990.

[15] 吴泽民, 张磊, 刘晗, 等. 基于随机Hough变换的三维集中式航迹起始算法[J]. 电子学报, 2013, 41(5): 840- 846. [Wu Ze-min, Zhang Lei, Liu Han, et al. Centralized 3D track initialization using random Hough transformation[J]. Acta Electronica Sinica, 2013, 41(5): 840-846.]

[16] 郭云飞, 郑晓枫, 彭冬亮, 等. 基于遍历Hough变换的弱目标检测前跟踪算法[J]. 系统仿真学报, 2015, 27(6): 1316-1323. [Guo Yun-fei, Zheng Xiao-feng, Peng Dong-liang, et al. Track-before-detect algorithm for weak target based on ergodic Hough transform[J]. Journal of System Simulation, 2015, 27(6): 1316-1323.]

[17] 于洪波, 王国宏, 张仲凯. 基于抛物线随机Hough 变换的机载脉冲多普勒雷达机动弱目标检测前跟踪方法[J]. 兵工学报, 2015, 36(10): 1924-1931. [Yu Hong-bo, Wang Guo-hong, Zhang Zhong-kai. A RPHT-TBD algorithm for tracking and detecting maneuvering weak target via airborne PD radar[J]. Acta Armamentarii, 2015, 36(10): 1924-1931.]

[18] Chen J, Henry L, Tiyus L, et al. A modified probabilistic data association filter in a real clutter environment[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(1): 300-313.

[19] Mark A R, James A S, William A H．Principles of modern radar[M]. Edison, New Jersey: Science Technology Publishing, 2010.

[20] 孔敏. 天波超视距雷达目标跟踪技术研究[D]. 烟台: 海军航空工程学院, 2007. [Kong Min. Research on target tracking technology for over-the-horizon radar[D]. Yantai: Naval Aeronautical and Astronautical University, 2007.]

AModifiedRandomizedHoughTransformTBDAlgorithmforHypersonicTargetinNearSpace

LI Yue-feng, WANG Guo-hong, LI Lin, ZHANG Xiang-yu

(Institute of Information Fusion, Naval Aeronautical and Astronautical University, Yantai 264001, China)

Aiming at the detection and tracking issue for near-space hypersonic target, a modified randomized Hough transform track-before-detect algorithm is proposed. Firstly, to overcome the large positional deviation from the angle error under long distance, measurements are mapped into the range-time plane with a higher accuracy by decoupling. Then, to merge the feature points in the parameter space more reasonably and improve the accumulation efficiency, the test statistics is built to compare with the adaptive threshold, so that the merging of the feature points is transformed into the adaptive mean difference hypothesis testing of two normal populations. Double integration means of noncoherent integration and binary integration is also adopted for the accumulation detection. Finally, to further reduce the false trajectories, motion constraints and trajectory merging are introduced for the final detected trajectory after sequence association. Simulation results show that, compared with the standard Hough transform track-before-detect algorithm, the proposed algorithm has fewer false trajectories and less run time with close detection probability.

Near space; Hypersonic target; Track-before-detect; Randomized Hough transform; Merging of feature points

V243.2; TN957

A

1000-1328(2017)10- 1114- 10

10.3873/j.issn.1000-1328.2017.10.012

2017- 07- 20;

2017- 08- 25

国家自然科学基金(61731023,61372027,61501489,61671462,61701519)；“泰山学者”建设工程专项经费资助项目

李岳峰(1992-)，男，博士生，主要从事目标检测与跟踪等方面的研究。

通信地址：山东烟台二马路188号海军航空工程学院信息融合研究所(264001)

电话：15506591185

E-mail:liyuefeng1992@126.com