采用SDRE方法的无径向推力最优轨道控制

张相宇，张 刚，曹喜滨

(哈尔滨工业大学卫星技术研究所，哈尔滨150001)

采用SDRE方法的无径向推力最优轨道控制

张相宇，张 刚，曹喜滨

(哈尔滨工业大学卫星技术研究所，哈尔滨150001)

针对无径向推力作用的两航天器轨道交会和编队卫星队形重构任务，采用状态依赖Riccati方程(SDRE)方法求解了其最优轨道控制问题。首先考虑J2摄动和推力仅存在于追踪航天器的周向和法向，推导了状态依赖配点(SDC)形式的非线性相对运动方程。然后针对终端状态为零的轨道交会问题，采用SDRE方法得到了最优反馈控制律，并给出了状态依赖Riccati微分方程的近似求解策略和数值求解策略。接着扩展了SDRE方法并将其用于终端状态不为零的编队卫星队形重构问题，并给出了相应的数值求解策略。相比于伪谱法等优化方法，本文提出的方法不需要初始猜测值。此外，数值仿真表明，解析求解Riccati微分方程方法对于近圆轨道具有较高的精度，数值计算方法对即使偏心率为0.3的椭圆轨道，其最优性偏差仍小于6%。

轨道交会；编队重构；状态依赖Riccati方程(SDRE)；周向推力；轨迹优化

0 引 言

为了实现两航天器的轨道交会或编队卫星的队形重构任务，通常采用能够产生三个方向推力的推力器配置形式或者采用单个推力器通过航天器的姿态调整，实现轨道控制所需的三个方向的推力。当航天器不便于在三个方向安装推力器且不便于通过姿态调整(如对地观测卫星的对地轴安装有相机，且在轨道机动过程中仍然保持对地定向任务)来实现三个方向的推力控制时，采用无径向推力的方式来进行轨道控制是一种较好的选择。但由于推力方向的特殊性使得系统的控制能力减弱，增强了模型的非线性特性，这给航天器的相对轨道控制带来了新的挑战。为了解决该问题，本文针对无径向推力条件下，航天器轨道交会或编队卫星的队形重构任务中的最优轨道控制问题展开研究。

对于仅包含周向推力的平面相对运动问题，Leonard等[1]提出将两个航天器之间的大气阻力差值等效为周向推力实现两个航天器的编队飞行。此后众多学者针对此类周向推力问题进行了研究[2-3]。对于其它形式的周向推力，Kumar等[4]设计了圆轨道编队飞行的线性反馈控制器。针对三维轨道控制，Starin等[5]设计了无径向推力下的圆轨道编队飞行线性二次型控制器(Linear quadratic regulator，LQR)，Godard等[6]设计了非线性控制器进行编队构型保持和队形重构。Huang等[7-8]研究了两航天器相对位置悬停和编队重构问题。以上研究均是基于圆轨道线性相对运动方程，少有考虑椭圆轨道的情况，且未考虑J2摄动的影响。此外，以上研究中的推力方向均考虑在目标航天器LVLH坐标系的周向和法向，并不是严格意义上追踪航天器的周向和法向。

在相对运动模型中，目标轨道为圆轨道时常采用C-W方程，椭圆轨道时常采用T-H方程。在考虑J2摄动的相对运动模型中，Schweighart和Sedwick[9]采用J2摄动的一阶近似扩展了C-W方程，得到了圆轨道下的线性相对运动方程，但未考虑摄动中短周期项的影响。Vadali[10]考虑了短周期项的影响得到了平均圆轨道的线性相对运动方程。Hamel和Lafontaine[11]采用平均轨道根数得到了考虑J2摄动的椭圆轨道相对运动方程。以上均是线性化的相对运动模型，对于非线性模型，Massari等[12]得到了状态依赖配点(State-dependent coefficient, SDC)形式的相对运动模型，但该模型仅考虑了J2摄动对目标航天器的轨道的影响，忽略了两航天器间J2摄动力的差值。Park等[13]虽然考虑了J2摄动力的差值，但未考虑J2摄动对目标航天器的轨道的影响。Xu和Wang[14]给出了一种精确的相对运动方程，但该方程不便于写成SDC的形式。

本文考虑推力在追踪航天器的周向和法向，建立SDC形式的非线性相对运动方程。扩展现有的SDRE方法得到终端状态为零和不为零的非线性最优反馈控制律，并给出终端状态为零的解析计算方法和两种情况下的数值求解策略。分别针对轨道交会和编队飞行队形重构问题进行仿真，以校验本方法对不同偏心率的主星轨道的求解精度。

1 无径向推力相对运动模型

1.1考虑J2摄动的相对运动模型

(1)

考虑J2摄动时，目标航天器的轨道角速度在LVLH坐标系三个方向的分量为[14]：

(2)

其导数为：

(3)

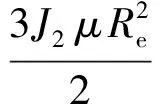
此外，式(1)中ud为作用于追踪航天器的推力加速度在目标航天器LVLH坐标系下的表示。当考虑推力仅存在于追踪航天器的周向和法向时，需对推力加速度作如下变换：

(4)

式中：uτ和un分别为追踪航天器的周向和法向推力加速度，Crel为追踪航天器LVLH坐标系到目标航天器LVLH坐标系的转换矩阵，其具体表达式将在下一节进行说明。

1.2动力学方程的SDC形式

基于SDRE方法的最优控制求解法可直接针对非线性系统进行，从而避免线性化带来的误差，但需将系统方程写成SDC形式，即状态变量乘以某个函数的形式。式(1)中与角速度相关的项已是SDC形式，本节给出二体引力加速度差值项和J2摄动加速度差值项的SDC形式以及转换矩阵Crel的二阶近似。

对式(1)中二体引力加速度差值项，采用文献[23]中的方法可以表示为：

(5)

式中：

α

(6)

(7)

(8)

对式(1)中J2摄动加速度项采用一阶线性近似：

(9)

对于追踪航天器LVLH坐标系到目标航天器LVLH坐标系的转换矩阵Crel，文献[24]给出了式(8)所示的二阶近似，其中(上标“-”)表示归一化处理后的值，其具体方法可参考文献[24]。

(10)

其中，系数A(x)和B(x)见式(11)和式(12)。

需要说明的是，本文给出的SDC形式的相对运动模型相比文献[13]进一步考虑了J2摄动对主星轨道角速度的影响；相比文献[12]中的模型，本文更全面的考虑了两航天器的J2摄动差分项。此外本文的模型并没有将二阶引力差值项进行线性化处理。

(11)

(12)

此外，本文的方法也适用于有径向推力的情况。此时可在式(4)中加入径向推力ur项，采用与本文类似的推导方法，仍然可得到形如式(10)的SDC形式的相对运动方程，后续基于SDRE的求解方法的推导过程也是一致的。

2 终端状态为零的SDRE控制方法

在两航天器的轨道交会任务中，要求在终端时刻两航天器的相对位置和相对速度为零，该问题等价于求解终端时间给定且终端状态为零的最优控制问题。

2.1状态依赖Riccati微分方程的建立

考虑如下的非线性系统：

(13)

其在初始时刻t0和终端时刻tf的状态满足：

(14)

以及最优控制的性能指标为：

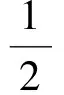
(15)

式中：x∈Rn、f(x)∈Rn和u∈Rm为向量，B(x)∈Rn×m为矩阵，Q∈Rn×n、S∈Rn×n和R∈Rm×m分别为对称正定矩阵。

将式(13)的系统写成如下SDC形式：

(16)

则由式(13)、(14)和(15)构成的最优控制问题可通过求解如下的Riccati微分方程得到[19]：

P(x,t)B(x)R-1BT(x)P(x,t)

(17)

且满足如下终端条件：

P(x,tf)=S

(18)

则所得的最优反馈控制律为：

u(x,t)=-R-1BT(x)P(x,t)x(t)

(19)

此外，由于该方法为反馈控制，因此对初始偏差也有一定的适应能力。

2.2状态依赖Riccati微分方程的近似求解策略

矩阵Riccati微分方程(17)的解通常得不到解析的表达式，可采用反向数值积分的方法从tf时刻积分到当前时刻t进行求解，其具体方法可参考下一节的图3并忽略其中的M(x,t)项，但该方法在每个控制周期都需要进行积分，具有较大的计算量。因此本节采用文献[19]提出的一种近似求解策略。

首先求解如下的代数Riccati方程：

Pss(x)A(x)+ATPss(x)-

Pss(x)B(x)R-1(x)Pss(x)+Q=0

(20)

将式(20)代入式(17)，可得：

AT(x)(P(x,t)-Pss(x))-

P(x,t)B(x)R-1BT(x)P(x,t)+

Pss(x)B(x)R-1BT(x)Pss(x)

(21)

与文献[19]所不同的是，为了避免在后续对P(x,t)-Pss(x)求逆的过程中出现奇异，本文并不直接求取式(20)的正定解，而采用文献[25]的方法求取其负定解。通过求取如下方程

-Pn(x)A(x)-ATPn(x)-

Pn(x)B(x)R-1(x)Pn(x)+Q=0

(22)

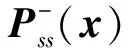
(23)

(24)

式(21)可以表示为：

B(x)R-1BT(x)

(25)

其终端条件为：

(26)

在方程(25)中令

(27)

则式(25)的解为：

(28)

式中:E为如下代数Lyapunov方程的解

(29)

至此，求得Riccati微分方程(17)的解为：

(30)

综上，解析求解Riccati微分方程(17)的步骤如图2所示。

3 终端状态不为零的SDRE控制方法

在编队飞行的队形重构任务中，绕飞航天器在给定的时间内相对主航天器从一个相对位置到达另一个相对位置从而实现新的构型。此时为了满足新的绕飞条件，终端状态通常不为零。假设追踪航天器的相对状态在初始时刻t0和终端时刻tf分别为：

(31)

式中:xf≠0。

取最优性能指标：

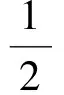
(32)

与式(15)不同的是，该性能指标中与状态x相关的项不再是标准的二次型的形式，因此第2节关于终端状态为零的SDRE方法并不能直接用于本节问题的求解。本节基于动态规划方法中的HJB方程，将文献[19]中标准的SDRE方法扩展到终端状态不为零的情形。

定义Hamilton函数：

(33)

其中,J*(x,t)称为最优值函数，由极大值原理：

(34)

得：

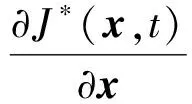
(35)

将式(35)代入式(36)，再由连续系统的HJB方程：

(36)

得：

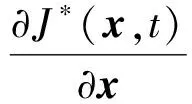
(37)

及其在t=tf时应当满足的边界条件为：

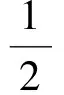
(38)

由于边界条件包含x的二次、一次、零次多项式的形式，因此假设最优值函数J*(x,t)具有如下与边界条件一致的形式：

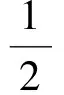
xT(t)M(x,t)+N(x,t)

(39)

为保证最优值函数满足边界条件(38)，其中P、M、N在终端时刻应当满足：

(40)

对式(39)关于状态x求偏导得：

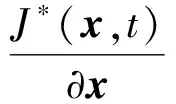
(41)

将式(41)和式(39)代入式(37)，通过对应项相等得：

(42)

其中，P、M、N在终端时刻满足式(40)的边界条件，相应的反馈控制可以表示为：

u=-R-1(x)BT(x)(P(x,t)x(t)+M(x,t))

(43)

由式(40)和式(42)可知：当xf=0时M(x,t)≡0，此时所得的控制律(43)与第2节的控制律(19)是一致的，因此第2节终端状态为零的SDRE方法是本节所得结果的特殊情形。此外，在式(42)中M(x,t)是P(x,t)的函数，因此很难求得M(x,t)的解析表达式。图3给出一种数值求解策略：在每一个正向积分步骤k中，先采用逆向数值积分的方法计算出从tf时刻到当前时刻tk的Riccati矩阵P(xk,tk)和M(xk,tk)，然后通过式(43)计算出本步长内的控制量uk。在此过程中目标航天器的轨道参数可通过事先求得的离散轨道参数插值得到。此外，在逆向积分过程中状态x在tf到tk间的值并不知晓，因此在逆向积分过程中将两航天器的相对状态固定为tk时的值x(tk)。此外，由于N(x,t)与M(x,t)和P(x,t)不耦合且并没有出现在式(42)的控制中，因此在逆向数值积分式(42)时，仅积分前两式以减小计算量。虽然该方法在每个控制周期都需要进行数值积分运算具有较大的计算量，但避免了优化过程中的初值猜测，因此仍然具有较大的实用价值。

4 数值仿真及结果分析

本节分别针对近距离轨道交会和编队飞行的队形重构问题进行仿真校验。其中轨道交会问题对应终端状态为零的情况，重构问题对应终端状态不为零的情况。在交会问题中将比较解析求解法、数值积分求解法和高斯伪谱法三种方法的优化结果，在重构问题中将比较数值积分求解法和高斯伪谱法的优化结果。高斯伪谱法采用佛罗里达大学开发的GPOPS优化软件。仿真中用到的基本物理参数为：地球半径Re=6378.13 km，地球引力常数为μ=3.986004×105km3/s2，摄动系数J2=1.082629×10-3。

4.1终端状态为零的轨道交会仿真

为了比较本文提出的算法对不同偏心率的目标航天器轨道的有效性，分别针对偏心率ec=0和ec=0.3两种情况进行了仿真。初始时刻目标航天器和追踪航天器的轨道参数如表1所示。

表1 初始时刻两航天器的轨道参数Table 1 The initial orbit elements of two spacecrafts

表1中,Hc为目标航天器的近地点高度，下标“c”表示目标航天器的轨道参数，下标“d”表示追踪航天器的轨道参数。设置轨道交会的初始时刻t0=0，终端时刻tf=1.3Tc，其中Tc为目标航天器的初始轨道周期。根据以上轨道参数可得初始的相对位置和相对速度在LVLH坐标系下的值如表2所示。

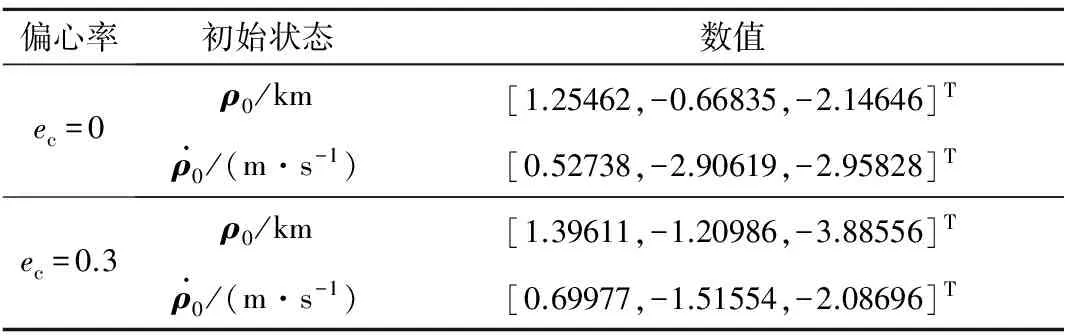
表2 初始时刻的相对位置和相对速度Table 2 The initial relative position and relative velocity

此外，对于燃料最优问题，性能指标函数(15)中应取Q=0且S为无穷大，但在解析求解法中为了保证Riccati方程解的存在性，并且考虑到位置和速度在数量级上的差别，取

(44)

在数值积分方法中不需要对Q进行限制，因此取Q=0，但S仍与式(44)一致。在伪谱法中由于方法原理的不同，可以直接在性能指标中不包含Q和S。

图4和图6分别为ec=0和ec=0.3时在目标航天器LVLH坐标系下的最优转移轨迹在三维坐标系和各个坐标平面内的投影。图5和图7分别为ec=0和ec=0.3时，作用在追踪航天器周向和法向的推力加速度曲线。由图4～7可知，三种控制方法下追踪航天器均与目标航天器实现了交会。此外将求得的控制量代入原始的非线性方程，当ec=0时，采用解析求解法得到的终端位置误差为[-0.03580,0.34287,-0.02413]Tm，终端速度误差为[-0.24981,6.19937,7.68697]T×10-5m/s；采用数值积分求解法得到的终端位置误差为[-0.03827,0.35629,-0.02517]Tm，终端速度误差为[-0.95065,5.49735,7.70494]T×10-5m/s，位置误差在分米量级。对于性能指标J，解析求解法为2.76415×10-3，数值积分求解法为2.47747×10-3，伪谱法为2.47736×10-3。数值积分求解法相对伪谱法的最优性偏差为0.004%。

当ec=0.3时，采用解析求解法得到的终端位置误差为[-0.05341,0.12008,-0.00334]Tm，终端速度误差为[-4.96389,1.53857,0.03782]T×10-3m/s；采用数值积分求解法得到的终端位置误差为[-0.11342,0.18104,-0.01197]Tm，终端速度误差为[-3.86410,5.62476,1.41895]T×10-5m/s。位置误差仍在分米量级。对于性能指标J，解析求解法为3.76989×10-3，数值积分求解法为9.72592×10-4，伪谱法为1.03204×10-3。数值积分求解法相对伪谱法的最优性偏差为5.8%。

由以上结果可知，随着偏心率ec的增大，解析计算方法和数值积分法的结果与伪谱法的偏差逐渐增大。数值积分法的偏差主要来自于每次逆向积分计算Riccati矩阵的过程中，将系数矩阵A(x,t),B(x,t)中的状态量x视为与当前时刻相等的常值，但实际中随着时间逐渐接近终端时刻，状态x是逐渐接近于零的。解析计算方法的偏差大于数值积分方法的偏差，主要原因是在解析计算Riccati矩阵的过程中，不仅将系数矩阵A(x,t),B(x,t)中的状态量x视为与当前时刻相等的常值，且将目标航天器的轨道参数也视为与当前时刻相等的常数。由式(11)和式(12)可知，对系数A21和A22的影响包含两航天器的相对位置x和目标航天器的轨道参数两部分，其中与目标航天器轨道角速度ωc相关的项是周期性变化的，且幅值随着偏心率ec的增大而增大。因此，在解析法求解过程的每一步将A(x,t),B(x,t)视为常数，其所得结果的最优性必然会随着偏心率ec的增大而降低。

虽然解析求解法的最优性会随着偏心率ec的增大而降低，但仿真过程中将其结果作为伪谱法的初值，使得伪谱法的收敛速度大大提高。

4.2非零终端状态的编队重构仿真

本节针对椭圆轨道下的编队飞行队形重构问题进行仿真，取初始时刻目标航天器和追踪航天器的轨道参数如表3所示。

表3 初末时刻两航天器的轨道参数(非零终端)Table 3 Initial and final orbit elements of the two spacecraft(non-zero terminal condition)

仿真初始时刻t0=0，终端时刻tf=1.2Tc。需要说明的是，上表中下标“c0”和“ct”分别表示主航天器在初始和终端时刻的轨道参数。根据以上参数，可以算出LVLH坐标系下的初末相对位置和相对速度如下：

(45)

由于在J2摄动下并不存在严格的周期绕飞条件，但通过以上方法得到的相对位置和相对速度在一个主航天器轨道周期内的偏差较小可近似认为是周期轨道。Q、S和R的取值与上一节一致。

图8为在主星LVLH坐标系下的最优转移轨迹在三维坐标系和各个坐标平面内的投影。图9为作用在追踪航天器周向和法向的推力加速度。由图8～9可知，数值积分求解法与伪谱法的结果非常一致，均可实现队形的重构任务。在推力加速度的量级上，周向推力小于4×10-4m/s2，法向推力小于1×10-4m/s2。此外将求得的控制量代入原始的非线性方程，数值积分求解法得到的终端位置误差为[-0.03490,-0.29369,-0.00802]Tm，终端速度误差为[-3.04687,-1.41242,-0.77204]T×10-5m/s，位置误差仍在分米量级。最优性指标方面，数值积分法为1.87632×10-4，伪谱法为1.80283×10-4，最优性指标的偏差为4.1%。此外在仿真过程中，采用数值积分法的结果作为高斯伪谱法的初值，使得高斯伪谱法能够快速的收敛。

虽然本文的方法需要进行数值积分，但相较于伪谱法，本文提出的方法并不需要进行初始猜测，因此具有很好的实用性。

5 结 论

1) 针对推力在追踪航天器的周向和法向的情况，建立了SDC形式的考虑J2摄动的非线性相对运动方程。

2) 基于SDRE方法给出了终端状态为零的轨道交会问题的近似解析求解方法。在近圆轨道下具有较好的最优性，尽管随着目标航天器偏心率的增大最优性降低，但仍可作为伪谱法等直接优化算法的初值。

3) 扩展了SDRE方法使之能够求解终端状态不为零的编队飞行队形重构问题，给出了数值求解策略。该方法不需要初始值猜测，在偏心率达到0.3时相较于伪谱法的最优性偏差仍小于6%。

[1] Leonard C L, Hollister W M, Bergmann E V. Orbital formationkeeping with differential drag[J]. Journal of Guidance, Control, and Dynamics, 1989, 12(1): 108-113.

[2] Bevilacqua R, Romano M. Rendezvous maneuvers of multiple spacecraft using differential drag underJ2perturbation[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(6): 1595-1607.

[3] 陈志明, 王惠南, 刘海颖. 基于大气阻力的微小卫星编队控制[J]. 应用科学学报, 2010, 28(2): 209-215. [Chen Zhi-ming, Wang Hui-nan, Liu Hai-ying. Satellite formation fly control based on atmospheric drag[J]. Journal of Applied Sciences, 2010, 28(2): 209-215.]

[4] Kumar K D, Bang H C, Tahk M J. Satellite formation flying using along-track thrust[J]. Acta Astronautica, 2007, 61(7-8): 553-564.

[5] Starin S R, Yedavalli R K, Sparks A G. Spacecraft formation flying maneuvers using linear quadratic regulation with no radial axis inputs[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Montreal, Canada, August 6-9, 2001.

[6] Godard, Kumar K D, Zou A. Robust stationkeeping and reconfiguration of underactuated spacecraft formations[J]. Acta Astronautica, 2014, 105(2): 495-510.

[7] Huang X, Yan Y, Zhou Y. Nonlinear control of underactuated spacecraft hovering[J]. Journal of Guidance, Control, and Dynamics, 2015, 39(3): 685-694.

[8] Huang X, Yan Y, Zhou Y. Analytical solutions to optimal underactuated spacecraft formation reconfiguration[J]. Advances in Space Research, 2015, 56(10): 2151-2166.

[9] Schweighart S A, Sedwick R J. High-fidelity linearizedJ2model for satellite formation flight[J]. Journal of Guidance Control and Dynamics, 2002, 25(6): 1073-1080.

[10] Vadali S R. Model for linearized satellite relative motion about aJ2-perturbed mean circular orbit[J]. Journal of Guidance Control and Dynamics, 2009, 32(5): 1687-1691.

[11] Hamel J, Lafontaine J D. Linearized dynamics of formation flying spacecraft on aJ2-perturbed elliptical orbit[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(6): 1649-1658.

[12] Massari M, Bernelli-Zazzera F, Canavesi S. Nonlinear control of formation flying with state constraints[J]. Journal of Guidance Control and Dynamics, 2012, 35(6): 1919-1925.

[13] Park H, Park S, Choi K. Satellite formation reconfiguration and station-keeping using state-dependent Riccati equation technique[J]. Aerospace Science and Technology, 2011, 15(6): 440-452.

[14] Xu G, Wang D. Nonlinear dynamic equations of satellite relative motion around an oblate earth[J]. Journal of Guidance Control and Dynamics, 2008, 31(5): 1521-1524.

[15] 雍恩米, 陈磊, 唐国金. 飞行器轨迹优化数值方法综述[J]. 宇航学报, 2008, 29(2): 397-406. [Yong En-mi, Chen Lei, Tang Guo-jin. A survey of numerical methods for trajectory optimization of spacecraft[J]. Journal of Astronautics, 2008, 29(2): 397-406.]

[16] 崔乃刚, 黄盘兴, 路菲, 等. 基于混合优化的运载器大气层内上升段轨迹快速规划方法[J]. 航空学报, 2015, 36(6): 1915-1923. [Cui Nai-gang, Huang Pan-xing, Lu Fei, et al. A hybrid optimization approach for rapid endo-atmospheric ascent trajectory planning of launch vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1915-1923.]

[17] 李俊峰, 蒋方华. 连续小推力航天器的深空探测轨道优化方法综述[J]. 力学与实践, 2011, 33(3): 1-6. [Li Jun-feng, Jiang Fang-hua. Survey of low-thrust trajectory optimization methods for deep space exploration[J]. Mechanics in Engineering, 2011, 33(3): 1-6.]

[18] Çimen T. Survey of state-dependent Riccati equation in nonlinear optimal feedback control synthesis[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(4): 1025-1047.

[19] Heydari A, Balakrishnan S N. Path planning using a novel finite horizon suboptimal controller[J]. Journal of Guidance Control and Dynamics, 2013, 36(4): 1210-1214.

[20] 张军, 徐世杰. 基于SDRE方法的挠性航天器姿态控制[J]. 宇航学报, 2008, 29(1): 138-144. [Zhang Jun, Xu Shi-jie. Control of flexible spacecraft via state-dependent Riccati equation technique[J]. Journal of Astronautics, 2008, 29(1): 138-144.]

[21] 刘利军, 沈毅, 赵振昊. 基于多项式拟合SDRE的三维导引律设计[J]. 宇航学报, 2010, 31(1): 87-92. [Liu Li-jun, Shen Yi, Zhao Zhen-hao. Three-dimensional missile guidance law design based on polynomial fitting of SDRE [J]. Journal of Astronautics, 2010, 31(1): 87-92.]

[22] 张银辉, 杨华波, 江振宇,等. 基于干扰估计的航天器大角度姿态机动鲁棒次优控制[J]. 宇航学报, 2015, 36(10): 1148-1154. [Zhang Yi-hui, Yang Hua-bo, Jiang Zhen-yu, et al. Spacecraft large angle attitude maneuver robust suboptimal control based on disturbance estimation [J]. Journal of Astronautics, 2015, 36(10): 1148-1154.]

[23] Franzini G, Innocenti M. Nonlinear H-infinity control of relative motion in space via the state-dependent Riccati equations[C]. IEEE 54th Conference on Decision and Control (CDC), Osaka, Japan,December 15-18, 2015.

[24] Sengupta P. Elliptic rendezvous in the chaser satellite frame[J]. The Journal of the Astronautical Sciences, 2012, 59(1-2): 216-236.

[25] Nguyen T, Gajic Z. Solving the matrix differential Riccati equation: a Lyapunov equation approach[J]. IEEE Transactions on Automatic Control, 2010, 55(1): 191-194.

OptimalOrbitalControlwithoutRadialThrustBasedonSDREMethod

ZHANG Xiang-yu, ZHANG Gang, CAO Xi-bin

(Research Center of Spacecraft Technology, Harbin Institute of Technology, Harbin 150001, China)

The optimal control problem of spacecraft rendezvous and formation reconfiguration without radial thrust is investigated by using the state dependent Riccati equation (SDRE) method. Considering the thrusters installed in the circumferential and normal directions, the nonlinear relative motion equations influenced byJ2perturbation are derived and presented via the state-dependent coefficient (SDC). Then the optimal feedback control law is derived by using the SDRE method, and an approximate analytical solution of the state dependent Riccati differential equation is obtained. Moreover, a numerical version of the obtained analytical solution is extended to solve the formation reconfiguration problem. Compared with the Gauss pseudospectral spectral method, the proposed method does not need an initial guess. Numerical results show that the analytical solution of the Riccati differential equation method has high precision for the near circular orbits, and the error of the optimal index of the numerical method is less than 6% even for the elliptical orbits with an eccentricity approaching to 0.3.

Orbital rendezvous; Formation reconfiguration; State dependent Riccati equation (SDRE); Circumferential thrust; Trajectory optimization

V448.234

A

1000-1328(2017)10- 1057- 11

10.3873/j.issn.1000-1328.2017.10.006

2016- 09- 12;

2017- 04- 21

国家自然科学基金(11402062,91438202)；重点实验室开放基金(HIT.KLOF.MST.201504)

张相宇(1986-)，男，博士生，主要从事航天器导航、制导与控制研究。

通信地址：黑龙江省哈尔滨市南岗区一匡街2号哈尔滨工业大学科学园B3栋507室(150080)

电话：(0451)86413440- 8507

E-mail: zxyuhit@163.com

张刚(1983-)，男，博士，副教授，主要从事航天器导航、制导与控制研究。本文通信作者。

通信地址：黑龙江省哈尔滨市南岗区一匡街2号哈尔滨工业大学科学园B3栋507室(150080)

电话：(0451)86413440- 8507

E-mail: zhanggang@hit.edu.cn