区域船舶扰动复杂度建模

刘 益， 黄 亮， 周春辉,2， 文元桥,2， 肖长诗,2

(1.武汉理工大学 航运学院，武汉 430063；2.内河航运技术湖北省重点实验室,武汉 430063)

区域船舶扰动复杂度建模

刘 益1， 黄 亮1， 周春辉1,2， 文元桥1,2， 肖长诗1,2

(1.武汉理工大学 航运学院，武汉 430063；2.内河航运技术湖北省重点实验室,武汉 430063)

为准确刻画和分析区域水上交通系统状态演化，从水上交通管理的视角建立基于船舶扰动的水上交通复杂度模型。该模型根据船舶扰动的作用机理，利用基于内禀属性的密度效应因子和迫近效应因子、响应效应因子描述区域水上交通系统在船舶扰动作用下的状态演化过程，综合考虑3个因子的耦合作用，绘制复杂性地图将交通状态可视化。试验结果表明，该模型能客观地刻画水上交通的复杂性，管理人员可借助复杂性地图直观地感知船舶的不同行为对系统的影响，并可预测不同管制措施的影响，为水上交通管理与分析提供一种新的方法和思路。

水路运输；复杂性；船舶扰动；迫近效应；响应

Abstract: To describe and analyze the evolution of marine traffic states accurately, the marine traffic complexity model reflecting ship disturbance is established from the angle of marine traffic management on the basis of the study about functional mechanism of ship disturbance. The model incorporates the factors reflecting the intrinsic properties of the relative speed and relative distance between ships-the density effect factor; the approaching effect factor and the response effect factor-and, therefore, describes the state evolution process of the marine traffic system under ship disturbance. The visualization of the traffic state is made by sketching the complexity map based on the comprehensive consideration of the coupling effect of above mentioned three factors. Experimental results show that this model can objectively present the complexity of marine traffic, and using the complexity map, managers can clearly perceive the influences of different ship behaviors on the system complexity, and predict the influences of different control measures, which is new for the management and analysis of the marine traffic.

Keywords: waterway transportation; complexity; ship disturbance; approaching effect; response

受船舶大型化、水上交通流密集化和航路增多等因素影响，某些区域的水上交通态势变得越来越复杂，给安全监管人员带来了巨大的工作压力。面对日益复杂的水上交通态势，监管人员不得不在短时间内处理大量信息，监管能效变得越来越低。从系统论的角度看，港口水域逐渐演变为复杂巨系统，船舶间的相互影响更加强烈，非线性关系越来越明显，呈现出复杂性。

复杂性体现在组成系统成分的数量多且相互关系密切，个体的简单行为在整体上涌现出与个体完全不同的特征。[1]复杂性科学理论为交通领域安全管理提供了新方法，已在航空领域得到大量研究应用。[2-5]复杂性测度可视为利用内禀属性对交通态势进行演进的客观描述，2000年DELAHAYE等[6-7]首次提出几何无序性测度方法，主要以相对位置和相对速度为指标，基于几何关系和性质来分析及描述航空器对之间的相互影响。随后，AIGOIN[8]在此基础上采用聚类方法对复杂度几何度量标准进行拓展，进一步探讨多航空器之间的复杂性关系。为更加真实地反映空域整体的复杂度，张进等[9]和ZHANG等[10]考虑交通流耦合关系，利用连携效应确定各航空器对之间的权重影响。LEE等[11]和HONG等[12]在几何无序性基础上创新性地提出交通扰动复杂性，通过描述系统对突发情况的响应间接测度复杂性，明确管制行为的反馈效应。水上交通领域的复杂性研究尚处于起步阶段，黄亚敏[13]及文元桥等[14]利用复杂性理论来定义水上交通认知复杂度和本质复杂度。综上所述，利用复杂性理论可深入分析交通系统内在特征，提高交通运输系统的控制和管理水平，但目前应用到水上交通管理领域中的研究较少。

对于区域水上交通态势的定量分析和研究，需从水上交通状态演化的角度分析系统复杂性的致因。对于某一区域水上交通系统，从管理人员的角度上说，当系统保持在一个稳定的状态时，其认知复杂性较低，外界船舶的扰动行为会打破其原有的平衡状态，导致系统复杂性增大，同时管理人员的管理难度也随之增大。因此，这里以管理人员的视角，利用船舶扰动的概念演绎区域水域交通系统对船舶的响应扰动，建立复杂度模型度量水上交通状态的改变，并借助复杂性地图将水上交通状态可视化，为船舶交通管理系统(Vessel Traffic System, VTS)监管人员提供更加准确、快速的辅助决策。

1 区域船舶扰动复杂性分析

1.1船舶扰动的基本概念

为更好描述扰动船舶的位置状态，以某点为中心，以研究的区域范围为半径，形成圆形扇区覆盖水域，图1为船舶扰动分析示意。所谓船舶扰动分析，是指当有外来船舶侵入到扇区水域内时，扇区交通系统对侵入行为作出响应，并通过复杂度模型观测和捕获这种响应。扰动船舶的状态由其侵入扇区的位置角E和方向角B确定，定义如下。

1) 位置角E是指按顺时针方向扰动船舶侵入扇区的位置与扇区圆心的连线和真北方向的夹角，E∈[0，2π)。

2) 方位角B是指扰动船舶侵入扇区的位置与扇区圆心的连线和扰动船舶航向之间的夹角，规定在侵入位置与圆心的连线的右边为正，在其左边为负,B∈[-π/2,π/2]。

3) 复杂性地图是记录扰动船舶从不同的位置角E和方位角B侵入扇区所导致的复杂度。

1.2扰动复杂性因子分析

水上交通系统蕴涵大量不确定性信息，具有明显的随机性和异质性，尤其是在突发状况下表现出敏感性和脆弱性。当有船舶突然侵入某一水域时，侵入行为最初只会影响少数船舶，但两船及多船之间的相互作用关系会形成多米诺效应，使扰动的影响迅速在整个水域展开，打破水上交通系统原有的平衡和稳定状态，致使交通态势发生变化。准确描述船舶间的相互作用关系对扰动复杂性测度至关重要，扰动船舶对扇区交通系统的影响过程大致分为以下3点。

1) 扰动船舶刚进入扇区，最明显、直接的影响是改变区域船舶聚集程度，在宏观上改变整个态势。

2) 扰动船舶与扇区内各船舶形成汇聚或汇离趋势，从而导致不同的迫近效应。

3) 为避免形成碰撞危险，扇区内必然会对船舶采取某些操船措施，响应扰动行为。

因此，这里采用聚集效应因子、迫近效应因子和响应效应因子描述扰动船舶的扰动影响。

1.3扰动复杂性的应用

扰动复杂性能演示水上交通系统的状态转变，可对水上交通状态进行预测。利用扰动复杂性分析，将某水域(如港口水域)设立为扇形区域，VTS等信息源能得到潜在扰动船舶的运动状态。通过船舶扰动复杂度模型，管理人员能感知扰动船舶对扇区内水域交通态势的影响，并据此指导扰动船舶航行，使其造成的影响最小。船舶扰动复杂性分析可演绎当前水上交通态势与未来水上交通态势之间的联系，管理人员可评估当前所采取的引导策略对未来水上交通造成的影响，预测一段时间内交通态势的变化。扰动复杂性分析能减轻管理人员的工作负荷，提高其安全管理水平和效率，同时符合智能航海发展要求。

2 基于船舶扰动的复杂性测度模型

2.1聚集密度建模

船舶越密集的水域，其交通态势越复杂。在水上交通工程中，交通流密度属于静态信息，并不能反映交通态势的动态变化，因为相同数量的船舶，聚集程度不同所对应的交通态势也不同。

假设有n艘船舶Si,i=1,2,…，n，其坐标为Si=[xi,yi],i=1,2,…，n，则所有船舶点的质心C的表达式为

(1)

若各船舶点与质心C的距离di=[xi-Cx,yi-Cy]，则聚集密度的表达式为

(2)

式(2)中：β=-2ln(0.5)/Lmax，Lmax表示可不考虑两船之间影响的足够大距离。

因此，扰动船舶所引起的聚集密度为

ΔGaden=Gaden(t0+Δt)-Gaden(t0)

(3)

式(3)中：Gaden(t0+Δt)和Gaden(t0)分别为扰动船舶进入扇区之前及进入扇区之后的聚集密度。

2.2迫近效应建模

扰动船舶Sd与扇区内各船Si的相互影响表现为迫近效应，分为汇聚和汇离趋势。

1) 当Sd与Si呈汇离趋势时，扰动影响较小，距离较大时可忽略；

2) 当Sd与Si呈汇聚趋势时，扰动影响明显，且汇聚趋势越紧急，交通态势越复杂。

扰动的迫近效应信息包含在Sd与Si的相对距离Ddi和相对速度vdi中，其中，Ddi体现两船在空间上的分布关系，而vdi则表征两船在时间上的关系。图2为扰动船舶与他船的相对关系，相对距离Ddi=Sd-Si，相对速度vdi=vd-vi。

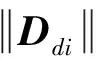
(4)

式(4)中：Ddi·vdi为向量内积；Ddi,vdi为vdi与Ddi的夹角。

2.2.1汇聚趋势

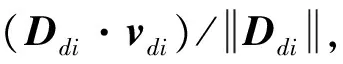
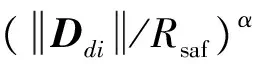
2.2.2汇离趋势

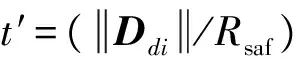
综上所述，扰动船舶的迫近效应因子可表示为

(5)

2.3响应效应建模

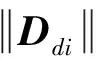
(6)

根据DELAHAYE等[7]的研究，得到响应效应因子Escdi的表达式为

(7)

2.4扰动复杂性测度模型

水上交通系统的复杂性很难通过单一因子度量，这里根据作用机理提出聚集密度因子ΔGaden，迫近效应因子Appdi和响应效应因子Escdi；扰动复杂度模型Comdi=f(ΔGaden，Appdi,Escdi)，综合宏观和微观交通要素。

1) 宏观上：聚集密度因子阐述扰动船舶与扇区整体交通系统的影响。

2) 微观上：Appdi从正面直接反映扰动船舶与扇区内船舶之间的紧迫程度；Escdi则从侧面印证扰动船舶与扇区内船舶之间的复杂态势，两者相辅相成，故对其取乘积关系；而聚集密度因子在宏观上影响整体水上交通系统，使其呈指数增加。

因此，扰动复杂性测度模型为

Comdi=(Appdi·Escdi-1)ΔGaden

(8)

2.5复杂度模型验证

试验情景见图3，设置3艘船舶，其中3号船舶为扰动船舶。水上交通态势随着扰动船舶位置的不同而发生变化，其变化情况见图3a，图3b～图3d分别为ΔGaden，Appdi及Escdi变化示意。当3艘船舶汇聚时，复杂度逐渐增加，并在t=17 min时达到最大值，此时2号船舶和3号船舶即将由汇聚状态转为汇离状态；在t=23 min时，3艘船舶完全处于汇离状态，此时复杂度曲线斜率有明显变化。图3e～图3h分别为t=5 min，t=10 min，t=15 min和t=20 min等4个时刻的水上交通状态。

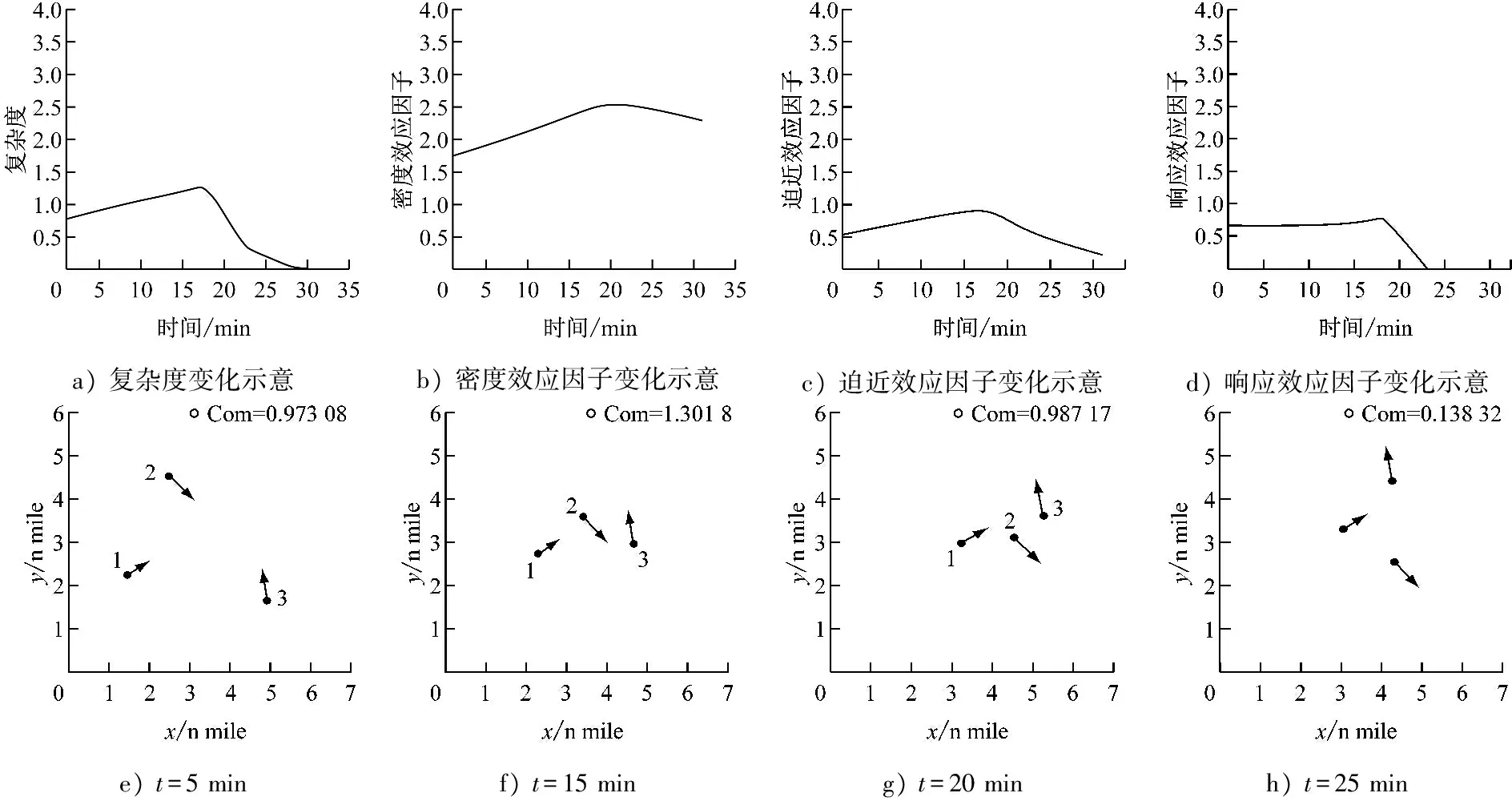
a)复杂度变化示意b)密度效应因子变化示意c)迫近效应因子变化示意d)响应效应因子变化示意e)t=5minf)t=15ming)t=20minh)t=25min

图3 水上交通状态演变

3 扰动复杂度在水上交通中的应用

利用仿真试验说明扰动复杂度在区域水上管理中的应用。基于复杂度地图信息，管理人员在整体上感知水域交通态势，并通知潜在扰动船舶以合适的位置角E和方位角B进入扇区，使造成的影响最小。实时复杂性地图符合智能航海要求。

3.1仿真试验假设

该船舶扰动试验主要针对航行在开阔水域的船舶，试验假设为：

1)船舶航向和航速保持不变。

2)扇区内船舶处在稳定状态。

3)忽略船舶驾驶员的操作反应等因素。

3.2试验设计

基于以上假设，可将区域水上交通情形抽象为图1。定义Si(t)=(xi(t),yi(t),vi(t),θi(t))为t时刻第i艘船舶的状态；xi和yi分别为船舶的横坐标、纵坐标；vi为船舶航速；θi为船舶真航向。设Sd进入和离开扇区的时间分别是t-ind和t-od，Si进入和离开扇区的时间分别是t-ini和t-oi。利用复杂性测度模型计算某一时刻扰动船舶Sd与Si之间的复杂度，计算式为

(9)

式(9)中：t1=max(t-ind,t-ini)；t2=min(t-od,t-oi)。

在计算得到扰动船舶与扇区内每艘船舶之间的复杂度之后，由于船舶彼此间的影响是非线性的，不能直接对其求和得到整体复杂度，故计算由扰动船舶引起的水上交通复杂度为

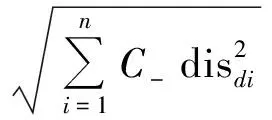
(10)

扰动船舶从某一位置角E和方位角B侵入到扇区内时，可按式(9)计算扰动船舶与每艘船舶之间的复杂度，并按式(10)得到扰动扰动复杂度。遍历所有可能的位置角E和方位角B，计算相应的复杂度，得到一个以位置角E和方位角B为变量的函数。将该函数用热度图形式表示出来，便得到一个二维的复杂性地图，其中横轴和纵轴分别为位置角E及方位角B。

3.3试验方案及结果分析

按照上述试验设计，设置图4a所示的水上交通情景，图中6个点代表6艘船舶的位置，其箭头方向和长度分别表示船舶航向和船速大小。按照上述扰动船舶试验的方法和理论，计算并绘制得到该区域水上交通情景的复杂性地图(见图5)。

基于复杂性地图，可明显感知到4个危险点(84，-16)，(150，45)，(330，-45)和(340,40)；同时，在复杂性地图左右两边各有1条深颜色条带，属于危险地带。结合图4可大致判断，以这2条条带所代表的位置角E和方位角B进入到扇区内的扰动船舶会与扇区内船舶发生明显的冲突，导致水上交通态势变得复杂。作为管理人员，应重点注意可能通过上述4个危险点所代表的位置角E和方位角B进入本船扇区的船舶，通过选择其他合适位置角和方位角进入来避免造成紧急危险局面。例如对原计划以(84，-16)(即图5中黑点1位置)进入到扇区内的船舶，可建议其以(85，-32)(即图5中白点位置)进入，扰动复杂度由9.3降到3.8，水上交通态势得到明显缓解。

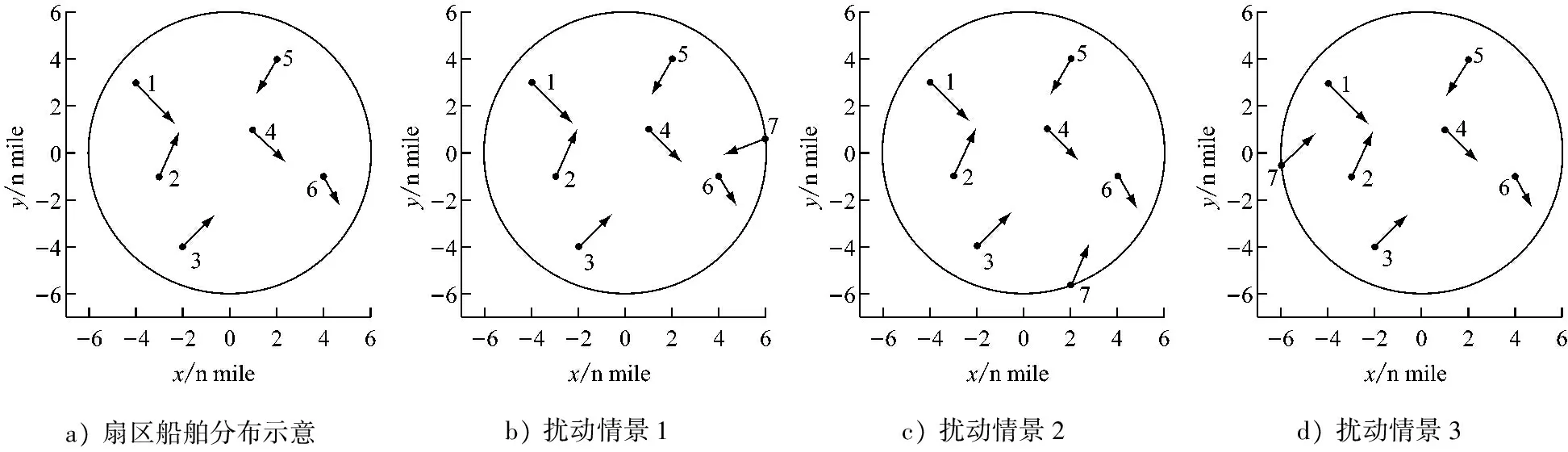
a)扇区船舶分布示意b)扰动情景1c)扰动情景2d)扰动情景3

图4 水上交通情景示意

为进一步解释复杂性地图，在图5所示的复杂性地图上选取高、中、低复杂度值点，即图中的黑色圆点1～3，图4b～图4d分别对应黑点1～3所代表的水上交通示意；此外，设置不同扰动船舶(7号船舶)。图4b中的扰动船舶会与1号、3号、4号、5号船舶形成碰撞危险，且会使扇区内交通结构变得复杂，彼此间的影响关系增加，导致扇区内水上交通态势顿时发生巨变，尤其是扰动船舶与4号船舶之间，由于距离较近且碰撞局面较难解脱，因此局面最紧急；图4c中的扰动船舶与3号和4号船舶形成碰撞危险局面，其中扰动船舶与3号船舶之间的航向夹角较小，碰撞危险局面将保持一段时间，会增加交通态势复杂性；而图4d中的扰动船舶不与扇区内船舶形成碰撞危险，仅与1号和2号船舶之间产生短时间的迫近效应，因此对应的复杂度较小。

4 结束语

基于密度效应、迫近效应和响应效应建立船舶扰动复杂度模型，研究区域水上交通系统状态在外界干扰下的演变状态。在水上交通安全研究方面，引入扰动复杂性分析理论，提供一种新的思路和方法，但同时也有许多地方需要改进和完善。这里忽略船舶的操纵性对试验的影响，仅简单将船舶作为质点，简化其运动特性。下一步将进一步考虑船舶扰动复杂性分析在航海中的应用，考虑船舶操纵性、气象环境的影响及数据的获取处理等因素。

[1] 梅拉妮.米歇尔. 复杂[M]. 唐璐，译. 长沙：湖南科学技术出版社，2012.

[2] 王红勇, 赵嶷飞, 温瑞英. 基于复杂网络的空中交通复杂性度量方法[J]. 系统工程, 2014(3): 16.

[3] 王姣娥, 莫辉辉, 金凤君. 中国航空网络空间结构的复杂性[J]. 地理学报, 2009, 64(8): 899-910.

[4] PRANDINI M, PIRODDI L, PUECHMOREL S, et al. Toward Air Traffic Complexity Assessment in New Generation Air Traffic Management Systems[J]. IEEE Transactions on Intelligent Transportation System，2011，12(3): 809-818.

[5] BRAZDILOVA SL, CASEK P, KUBALCIK J. Air Traffic Complexity for a Distributed Air Traffic Management System [J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering，2011，225(G6): 665-674.

[6] DELAHAYE D, PUECHMOREL S. Air traffic complexity: Towards Intrinsic Metrics[C]//Proceedings of the Third USA/Europe Air Traffic Management R & D Seminar, 2000.

[7] DELAHAYE D, PUECHMOREL S, HANSMAN J, et al. Air Traffic Complexity Map Based on Non Linear Dynamical Systems[J]. Air Traffic Control Quarterly,2016,12:284-303.

[8] AIGOIN G. Air Traffic Complexity Modeling[D]. Toulouse: Ecole Nationale de l’Aviation Civile，2001.

[9] 张进, 胡明华, 张晨, 等. 空域复杂性建模[J]. 南京航空航天大学学报, 2010, 42(4): 454-460.

[10] ZHANG C, ZHANG J, HU M. Air Traffic Complexity Based on Alliance Effects[C]//Digital Avionics Systems Conference, 2009.

[11] LEE K, FERON E, PRITCHETT A. Air Traffic Complexity: An Input-Output Approach[C]//American Control Conference, 2007: 474-479.

[12] HONG Y, KIM Y, LEE K. Conflict Management in Air Traffic Control Using Complexity Map [J]. Journal of Aircraft，2015,52(5):1-11.

[13] 黄亚敏. 水上交通复杂性测度研究[D].武汉:武汉理工大学，2014.

[14] 文元桥，黄亚敏，杨君兰,等. 水上交通流结构复杂度建模[J]. 中国航海，2014,37(2): 62-66.

ModelingofShipDisturbanceComplexityinWaters

LIUYi1，HUANGLiang1,ZHOUChunhui1,2，WENYuanqiao1,2，XIAOChangshi1,2

(1. School of Navigation，Wuhan University of Technology，Wuhan 430063，China； 2. Hubei Key Laboratory of Inland Shipping Technology，Wuhan 430063，China)

黄 亮(1986—),男,湖北孝昌人,博士后,主要从事船舶航迹分析与可视化研究。E-mail:plaquemine@whu.edu.cn

U661.1；U698

A

2016-11-26

国家自然科学基金(57579204);中国博士后科学基金(2016M602382);武汉理工大学自主创新基金(2016IVA064)

刘 益(1990—),男,湖北广水人,硕士生,主要从事水上安全理论、水上交通大数据分析研究。E-mail:fly_ly@whut.edu.cn

1000-4653(2017)01-0042-05