船舶运动模拟器运动学正解数值解法对比分析

党婴龙， 徐合力， 高 岚

(武汉理工大学 能源与动力工程学院， 武汉 430063)

船舶运动模拟器运动学正解数值解法对比分析

党婴龙， 徐合力， 高 岚

(武汉理工大学 能源与动力工程学院， 武汉 430063)

为研究船舶运动模拟器运动学正解的数值解法，建立其运动平台的数学模型，将运动学正解问题转化为非线性方程组的无约束最优化问题。分别采用数值迭代算法中的牛顿法、逆Broyden秩1法、Broyden-Fletcher-Shanno(BFS)秩2法及Broyden-Fletcher -Goldfarb-Shanno(BFGS)法进行求解，运用MATLAB编程并采用同一数值模型对这4种算法进行对比分析。分析结果表明：4种算法在工作空间内都收敛且数值稳定，BFS秩2法的迭代效率最高，BFGS法可用于奇异场合。通过仿真试验对各算法进行适当的修改，优化各算法的迭代效率并增加其对初值的鲁棒性，为位姿正解应用于实时控制场合提供理论指导。

运动学正解； 牛顿法； 逆Broyden秩1法； BFS秩2法； BFGS； 优化

Abstract: In order to investigate the numerical methods for solving direct kinematics problems of the ship motion simulator, a mathematical model of the motion platform is established and the kinematics problems are transformed to the unconstrained optimization problem of the nonlinear equations. The Newton method, single rank inverse Broyden, rank-two BFS and BFGS method are used to solve the problem respectively and the MATLAB program is used to verify and compare the algorithms with the same numerical model. The analysis results show that all the algorithms are convergent and stable in the workspace, while rank-two BFS shows the highest efficiency. The BFGS method can be used in singular cases. Through experiments, all the algorithms are modified and optimized for better iterative efficiency and the robustness to initial valuses.

Keywords: direct kinematics; Newton method; single rank inverse Broyden； rank-two BFS； BFGS； optimization

船舶运动模拟器主要用于舰船设备测试和海员教学培训，可减少实船试验次数、缩短设备开发周期、提高海上搜救人员的适应能力和业务素质。运动学正解问题是研究运动模拟器动力学、轨迹规划和位姿控制等内容的重要基础，因此进行船舶运动模拟器的运动学正解研究具有重要意义。

受模拟器运动平台结构特性的影响，其运动学逆解问题容易求解，而正解问题较难求解，因此可利用逆解公式进行杆长逼近，反向求出满足一定精度要求的正解，这实质上是牛顿法的应用。[1]利用牛顿法求解时每次迭代都需求一次逆矩阵，运算量较大；拟Newton法包括逆Broyden秩1法、Broyden-Fletcher-Shanno (BFS)秩2法和Broyden-Fletcher-Goldfarb-Shanno (BFGS)法等，相比牛顿法，其运算量大大减少，迭代速度也明显提高。[2]为观察各算法的迭代效率，采用统一的误差对这些算法进行对比分析。由于模拟器运动方程具有高维和耦合性，3种拟Newton法标准算法的初始方向选取规则不能保证收敛，因此通过仿真试验修改3种拟Newton法的初始迭代方向选取规则，这不仅能优化迭代效率，而且可扩大初值的取值范围。此外，在BFGS法的迭代过程中采用非单调搜索并加入扰动项和重复生成策略,以保证收敛。

1 运动学正解模型

船舶运动模拟器用来模拟船舶在海浪中的摇晃运动，其核心设备是一个Stewart并联机构。该机构主要由2个平台和6个支杆构成，驱动单元通过驱动6个支杆的伸缩使上平台完成空间6个自由度的运动模拟。依据典型的6-6型Stewart平台建立模型，图1为该平台机构简图，其中上平台和下平台的各绞点连接起来构成2个六边形,设r1和r2分别为2个六边形所对应的外接圆半径,θ1和θ2分别为2个六边形短边所对应的圆心角，上平台和下平台六边形隔点相连构成2个正三角形。分别在上平台和下平台上建立坐标系O′-x′y′z′和O-xyz，O′和O分别为2个六边形的外接圆圆心，设O′的绝对坐标为(x0,y0,z0)，O的绝对坐标为(0,0,0)。O′x′轴和Ox轴分别取线段B1B6及A1A6的中垂线方向且指向平台外部,O′z′轴和Oz轴分别垂直于上平台及下平台且方向朝上,O′y′轴和Oy轴的方向根据右手规则确定，初始位置处上平台与下平台互相平行。Ai为上平台的第i个铰点在O-xyz中的坐标,Bi为下平台的第i个铰点在O-xyz中的坐标。上平台位姿设为X(x,y,z,α,β,γ)。R为由坐标系O′-x′y′z′到坐标系O-xyz的齐次变换矩阵。则

(1)

式(1)中: c为cos；s为sin。

图1 Stewart平台机构简图

2 算法简介及优化

2.1牛顿法

对于非线性方程组F(x)=0，满足

(2)

式(2)中：n≥2。其牛顿迭代式为

xk+1-xk=-(F′(x))-1F(x)

(3)

牛顿法迭代程序：

2) 计算xk+1=xk+dk，dk=-F′(xk)F(xk)，F(xk+1)，F′(xk+1)。

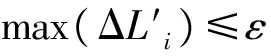
2.2逆Broyden秩1法

逆Broyden秩1法迭代程序:

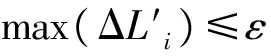
一般情况下，初始方向选取为H0=I或H0=(F′(x0))-1。[3]当迭代初值远离最优解时，该选取规则可能失效，造成结果不收敛。为增加算法对初值的鲁棒性，规定初始方向选取新规则：

1)H0=(F′(x0))-1。

3) 根据模型需要，选取a=100。

新规则将远离最优解的初值的方向矩阵替换为平台初始点的方向矩阵，经多组初值检验发现，新规则既可优化迭代效率，又能增强算法对初值的鲁棒性。

2.3BFS秩2法

BFS秩2法迭代程序:

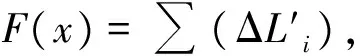
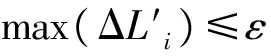
初始方向选取新规则[4]：

1)H0=(F′(x0))-1，记号变量Δ=0。

3) 当Δ=1且迭代次数k>m时，Hk+1=Hk，根据需要选取m=2。

新规则将远离最优解的初值方向矩阵替换为平台初始点的方向矩阵，并在迭代过程中保留和维持一个优化的迭代方向，增强了算法对初值的鲁棒性。

2.4BFGS法

BFGS法是求解无约束最优化问题最有效的方法之一，但对非凸函数的最优化问题不具有全局收敛性，当目标函数在迭代过程中存在细长、弯曲的峡谷时,采用单调性搜索算法会大大降低计算效率。非单调线性搜索不要求函数值在每步迭代中都单调下降，这使得步长因子的选取更具有弹性。因此，为优化算法的迭代效率，需采用非单调搜索算法并加入扰动项和重复生成策略。[5-6]

BFGS法迭代程序:

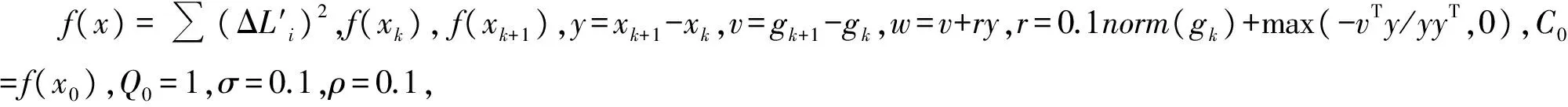
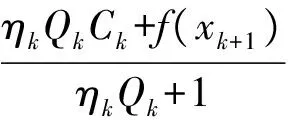
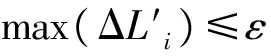
7) 输出xk+1和f(xk+1)，结束。

由于方向矩阵的位置分量与姿态分量的变化范围不同，对目标函数的影响系数也不同，因此BFGS算法的初始方向不能按一般规则直接选择单位矩阵I，这里规定初始方向H0选取的新规则为

n=round(lg(max(g0(4),g0(5),g0(6))))

(4)

(5)

采用重复生成策略为

(6)

(7)

式(5)～式(7)中：s=3；x=3。

经过仿真试验，采用新规则可在迭代过程中跳出峡谷现象并收敛于最优解，与标准BFGS法相比，可大大提高迭代速度和初值的鲁棒性。

3 数值算例及分析

给定Stewart平台数据为：r1=250 mm,r2=270 mm,θ1=π/4，θ2=π/5，Lmax= 370 mm,Lmin= 300 mm。给定各杆长为:L1=331.777 1 mm,L2=324.103 0 mm,L3=358.139 2 mm,L4=338.397 0 mm,L5=329.075 2 mm,L6=356.475 7 mm。

为比较各算法的迭代效率，统一设定误差为max(ΔLi′)。程序存在舍入误差，经数据验证后得知最大精度等级约为10-13。定义max(ΔLi′)的大小作为初值距离最优解远近的标准。[7-8]

初值选取7个点：1个为平台最初起点[0，0，322.6，0，0，0]；2个在最优解[50， 50， 320，0，0，0]附近，分别为[49，49，319， 0，0，0]和 [49.9，49.9，319.9，0，0，0]；2个在工作空间内随机选取，其中一个离最优解较近，另一个离最优解较远，分别为[48，47，321，0.01， 0.03，0.05]和[4，5，320，0.1，0.05，-0.03]；2个在工作空间外选取，一个离最优解较近，另一个离最优解较远，分别为[53，44，326，0.1，0.05，-0.03]和[55，55， 325，1，1，1]。各算法使用同一台计算机，CPU为Inter(R)G630，主频为2.70 GHz，内存为4 GB，操作系统为Windows XP。4种算法迭代效率比较见表1。

表1 4种算法迭代效率比较

由表1可知：

1) 在相同的初值和误差要求下，BFS秩2法的迭代时间最短、效率最高；牛顿法的迭代次数最少；BFGS法的迭代次数最多且用时较长。

2) 各算法的迭代效果均与初值有关，离最优解较近则迭代效果较好，远离最优解则可能不收敛或收敛于其他解，因此初值应尽量在最优解附近。

3) 各算法对初值的要求均不高，在工作空间内即可。

为观察各算法的具体迭代过程，选取初值为[49，49，319，0，0，0]，绘出其迭代对比图及局部放大图见图2和图3。

图2 初值为[49，49，319，0，0，0]时的迭代对比图

图3 初值为[49，49，319，0，0，0]时的迭代对比局部放大图

为说明BFGS法的优点，取奇异点[0，0， 0，0，0，π/2]作为迭代目标位姿。选取最优解附近点[0.1，0.1，0，0，0，1.57]作为迭代初值。[9-10]此时牛顿法、逆Broyden秩1和BFS秩2法全部失效，只有BFGS法依然有效。由奇异特性可知，初值点的位置分量中z轴分量在奇异曲线附近影响系数变大，因此在初始方向选取规则和重复生成策略中需对z轴分量和姿态分量作出相同变换,即令式(5)～式(7)中的s=2,x=4。其迭代过程见图4。

图4 初值为[0.1,0.1,0,0,0,1.57]的迭代图

4 结束语

以上4种数值迭代算法在工作空间内非奇异处均收敛，迭代结果均可达到较高的精度等级,而在实际控制中，可直接选用上一时刻的位姿数据作为迭代初值，根据机构运动的连续性，其迭代结果就是所需的最优解。

BFS秩2法用时最短，优于其他算法，对实时控制具有重要意义，但初始时仍需求一次逆矩阵，当初始方向矩阵奇异或病态时易迭代失败。BFGS法用时虽较长，但无需求逆矩阵，当初值在奇异边界附近时依然有效，这对模拟器机构奇异分析和初期设计具有重要意义。

[1] 姜虹，贾嵘，董洪智,等. 六自由度并联机器人位置正解的数值解法[J].上海交通大学学报，2000，34(3)：351-353.

[2] 耿明超，赵铁石，王唱，等.基于拟Newton法的并联机构位置正解[J].机械工程学报，2015,51(9):28-36.

[3] 王斌.非线性方程组的逆Broyden秩1拟Newton方法及其在MATLAB中的实现[J].云南大学学报(自然科学版)，2008,30(S2): 144-148.

[4] 王斌.非线性方程组的BFS秩2拟Newton方法及其在MATLAB中的实现[J].云南民族大学学报(自然科学版)，2009,18(3):213-217.

[5] 孙惠娟.求解非凸无约束优化问题的非单调BFGS方法[D].开封：河南大学，2008.

[6] YUAN GL,WEI ZX.Convergence Analysis of a Modified BFGS Method on Convex Mini-Mizations[J].Computational Optimization and Applications，2010,47(2):237-255.

[7] 杨伍梅，刘权.基于MATLAB的无约束优化问题对称秩-1法与BFGS法之探讨[J].怀化学院学报，2015,34(5):24-26.

[8] SEKHAR DC. GANGULI R. Modified Newton, Rank-1 Broyden Update and Rank-2 BFGS Update Methods in Helicopter Trim:A Comparative Study[J].Aerospace Science and Technology，2012,23(1):187-200.

[9] 曹毅.六自由度并联机器人奇异位形的研究[D].秦皇岛:燕山大学，2005.

[10] MA Jianming,HUANG Qitao,XIONG Haiguo.Analysis and Application of the Singularity Locus of the Stewart Platform[J].Chinese Journal of Mechanical Engineering，2011,24(1): 133-140.

ComparativeAnalysisofNumericalMethodsforDirectKinematicsinShipMotionSimulator

DANGYinglong,XUHeli,GAOLan

(Energy and Power Engineering College ,Wuhan University of Technology,Wuhan 430063,China)

TP242.2;U666.158

A

2016-12-11

党婴龙(1988—)，男，河南洛阳人，硕士生，主要从事船舶自动化研究。E-mail：399811043@qq.com 徐合力(1963—)，男，湖北武汉人，高级实验师，主要研究方向为轮机工程船舶辅助机械系统。E-mail：406176290@qq.com

1000-4653(2017)01-0106-04