电控陀螺罗经稳定过程研究与设计

袁群哲， 周红进， 蒋永馨， 韩云东

(海军大连舰艇学院 航海系，辽宁 大连 116018)

电控陀螺罗经稳定过程研究与设计

袁群哲， 周红进， 蒋永馨， 韩云东

(海军大连舰艇学院 航海系，辽宁 大连 116018)

为提高电控陀螺罗经的使用性能，根据罗经力矩方程解析出主轴运动方程，建立罗经主轴运动仿真模型，仿真研究力矩系数、启动初始条件与罗经稳定精度、阻尼运动周期及稳定时间的关系。仿真结果表明：随着纬度升高，罗经的稳定精度下降，稳定时间显著延长；但通过同步放大2倍找北力矩和阻尼力矩系数，在保持稳定精度不变的同时，约缩短稳定时间30%；初始方位角和高度角并不影响罗经的稳定精度和阻尼周期，主要影响稳定时间，且初始高度角对稳定时间的影响更加显著。启动罗经时，应先调整陀螺仪主轴至水平位置；主轴水平后，随着初始方位角的减小，稳定时间能缩短50%以上。此外，为电控罗经设计力矩系数自适应调整机构和初始高度角、方位角调整机构，可灵活提高罗经的稳定性，按照先水平后找北的流程启动罗经能有效缩短罗经稳定时间。

电控陀螺罗经；力矩系数；稳定位置；阻尼运动周期；稳定时间

Abstract: The simulation model is set up based on the motion equations of the spinning axis of the gyroscope with Simulink. The investigation is focused on the relation among the moment coefficients, the initial conditions and the key performances, such as static accuracy, damped oscillation period and settling time. The simulation results show that as the latitude goes up the settling time and the static error increase, but the performance can be improved by adjusting the moment coefficients. Doubling the moment coefficients will shorten the settling time by about 30 percent while keeping the static accuracy. The simulation results also show that initial azimuth and elevation of the spinning axis of gyroscope do not affect the static accuracy and oscillation period, but do effect the settling time. Compared to the azimuth angle, the elevation angle shows more effect on the settling time. The settling time can be reduced more than 50 percent if the axis of gyroscope is appropriately leveled. It is strongly recommend that the axis of gyroscope should be leveled first before oriented to north when starting up an electrically torqued gyrocompass. Further, the starting up process of an electrically torqued gyrocompass can be significantly improved if moment coefficient self-adjusting unit and initial orientation adjusting unit are designed.

Keywords: electrically torqued gyrocompass； moment coefficient；settling point； damped oscillation period； settling time

电控陀螺罗经是航海中常用的一种罗经，阻尼周期、稳定时间和稳定精度是衡量其工作性能的主要指标。舰船在执行任务时会遇到各种突发状况，比如：在靠码头状态下紧急出航时，需要快速启动罗经；在海上航行时罗经发生故障，紧急修复后需要动态启动罗经。不论何种情况，用户最关心的通常是罗经的稳定时间和稳定精度。因此，如何在各种复杂情况下保证(甚至是提高)罗经的性能指标是需要思考的问题。对此，研究电控陀螺罗经的稳定过程，提出改进罗经性能的设计方法及在不同工作条件下启动罗经的方法和注意事项。

1 主轴运动方程

为使陀螺罗经稳定指北，须在陀螺转速稳定后对其施加找北力矩和阻尼力矩。对于电控陀螺罗经，一般采用短轴阻尼的方式，因此找北力矩和阻尼力矩均与陀螺仪主轴的高度角成正比关系。

记找北力矩为My，阻尼力矩为Mz，陀螺仪动量矩为H，则在静止状态下启动电控陀螺罗经，主轴运动方程[1]为

(1)

(2)

(3)

式(1)～式(3)中：α为陀螺仪主轴方位角，陀螺仪主轴相对子午面偏西为正、偏东为负；θ为陀螺仪主轴高度角，陀螺仪主轴相对水平面下俯为正、上仰为负；φ为地球纬度；Ky和Kz为找北力矩系数及阻尼力矩系数；ωez为地球自转角速度在当地水平地理坐标系中的垂向分量；ωeN为地球自转角速度在当地水平地理坐标系中的北向分量。

(4)

式(4)中：C1,C2,C3,C4与主轴初始方位角和高度角有关。

(5)

式(5)中：C1,C2,C3,C4与主轴初始方位角和高度角有关。

(6)

式(6)中：C1,C2,C3,C4与主轴初始方位角和高度角有关。

根据式(1)可确定陀螺罗经的稳定位置、阻尼运动周期及稳定时间等主要的性能参数。[2-6]

1.1稳定位置

求解式(1)，虽然方位角和高度角具有不同形式的解，但稳定位置是相同的，记稳定后的方位角和高度角分别为αpφ及θp，则有

(7)

1.2阻尼运动周期

施加阻尼力矩后，陀螺仪主轴运动为周期性衰减振荡运动，最终会稳定在(αpφ,θp)处，方位角相邻3次经过稳定点的时间间隔即为阻尼运动周期T。

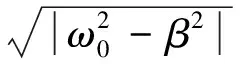
(8)

1.3稳定时间

稳定时间是指陀螺罗经从启动到稳定至稳定位置所需的时间，航海中通常指罗经从启动到主轴运动到稳定点±1°以内的时间。具体的数值可通过仿真获得。

根据式(1)及式(4)～式(8)可建立电控陀螺罗经仿真模型，研究力矩系数变化对罗经稳定过程的影响及不同初始条件下罗经的稳定过程。下面以某型电控陀螺罗经的结构参数为例，仿真研究力矩系数变化和不同初始条件下罗经的稳定过程，分析其稳定位置、阻尼运动周期和稳定时间的变化。该电控罗经的结构参数为

(9)

2 力矩系数变化与罗经稳定过程

由于找北力矩和阻尼力矩的大小均与陀螺仪主轴高度角成正比例关系，因此一般通过改变力矩系数来调节找北力矩和阻尼力矩的大小。[7-9]

仿真初始条件为：α0=5°,θ0=5°,φ=38.9°。图1为找北力矩系数和阻尼力矩系数不变、找北力矩系数放大2倍而阻尼力矩系数不变及找北力矩系数和阻尼力矩系数同时放大2倍等3种情况下陀螺仪主轴方位角随时间变化的曲线，仿真持续时间为86 400 s，仿真纬度为38.9°N。表1为罗经稳定性能参数与力矩系数变化关系。

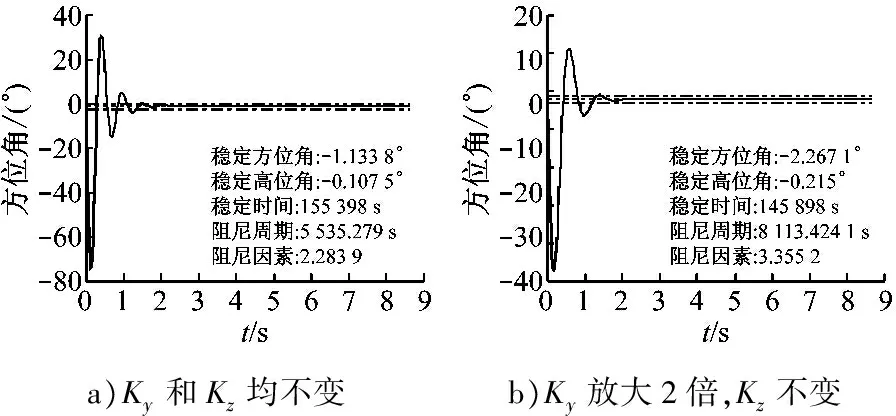
a)Ky和Kz均不变b)Ky放大2倍，Kz不变

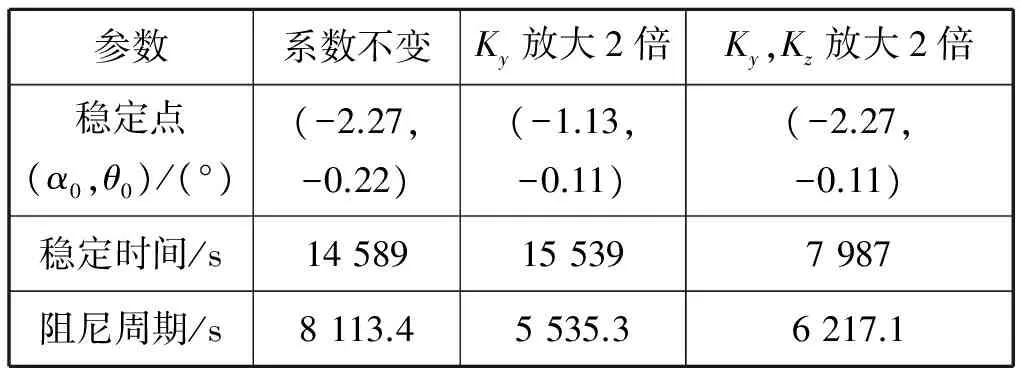
表1 罗经稳定性能参数与力矩系数变化关系

图1表明：在同一纬度启动电控陀螺罗经，找北力矩放大2倍后，稳定位置更加接近于水平指北的方向，即稳定精度提高、阻尼周期缩短，但稳定时间延长；若同时放大找北力矩和阻尼力矩，则可保持稳定位置不变、阻尼周期和稳定时间缩短。

3 初始条件与罗经稳定过程

电控陀螺罗经启动的初始条件主要有纬度、初始方位角和初始高度角。初始条件不同，启动陀螺罗经时稳定过程也不相同。

3.1纬度与罗经稳定过程

仿真条件为：α0=5°,θ0=5°，φ=(0°,38.9°,60°,70°)。图2为不同纬度条件下陀螺仪主轴方位角随时间变化的曲线，仿真持续时间为86 400 s。表2为罗经稳定参数与纬度变化关系。

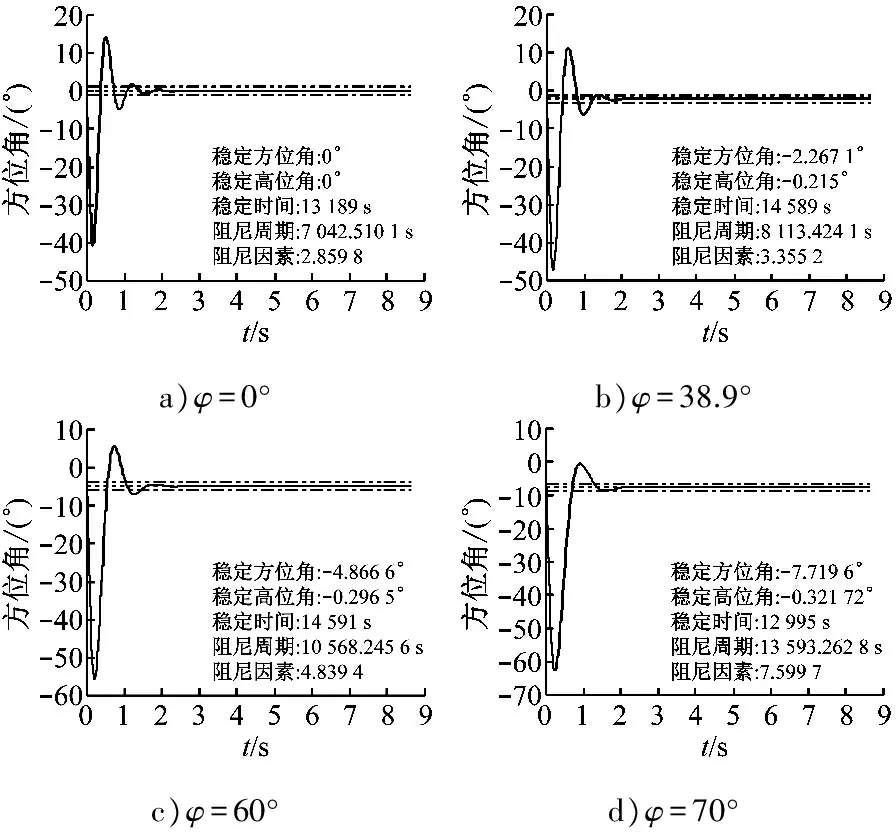
a)φ=0°b)φ=38．9°c)φ=60°d)φ=70°

图2 方位角曲线

图2表明：在不同纬度启动电控陀螺罗经，其稳定位置和稳定时间也不相同。纬度为0°时，稳定位置为(0°，0°)，即陀螺仪主轴水平指北，稳定时间约为13 189 s；随着纬度升高，稳定位置逐渐偏离水平指北的位置，阻尼运动周期和稳定时间随之增大；纬度为80°时，稳定位置为(-15.93°，-0.34°)，稳定时间为18 199 s，相比赤道处稳定时间增大50%，稳定位置严重偏离真北15°。这表明在高纬度地区启动电控陀螺罗经，需花费更长的时间才能稳定，且稳定精度较低。

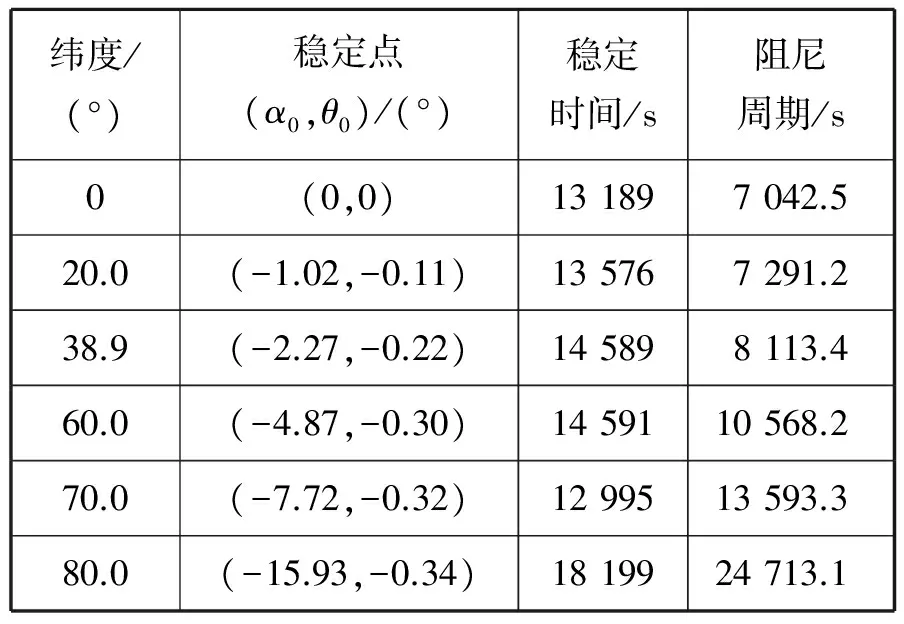
表2 罗经稳定参数与纬度变化关系

3.2初始偏差角与罗经稳定过程

初始偏差角是指陀螺罗经启动时陀螺仪主轴的初始指向，包括初始方位角和初始高度角。初始方位角和高度角不同，表明陀螺仪主轴的初始指向也不同。初始指向也会影响罗经的稳定过程，主要影响稳定时间。

3.2.1初始方位角与罗经稳定过程

仿真条件1：θ0=5°,φ=38.9°，α0=(0°,5°,20°,40°)。图3为方位角曲线。

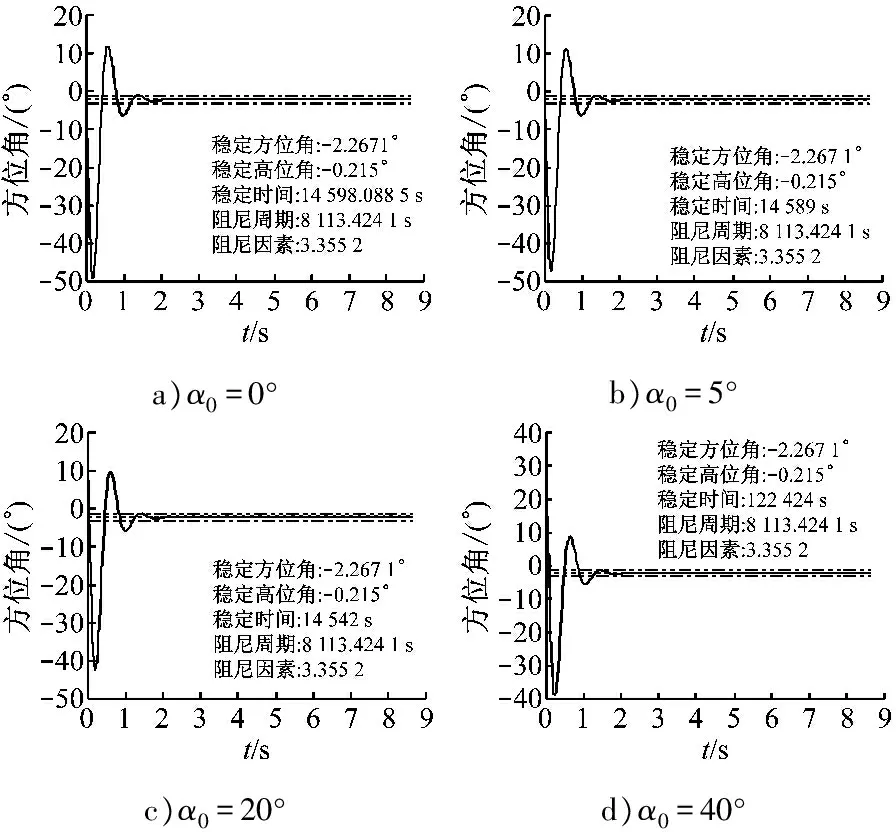
a)α0=0°b)α0=5°c)α0=20°d)α0=40°

图3 仿真条件1下的方位角曲线

仿真条件2：θ0=0°,φ=38.9°，α0=(0°,5°,20°,40°)。图4为方位角曲线。

3.2.2初始高度角与罗经稳定过程

仿真条件3：α0=5°,φ=38.9°，θ0=(0°,5°,20°,40°)。图5为高度角曲线。

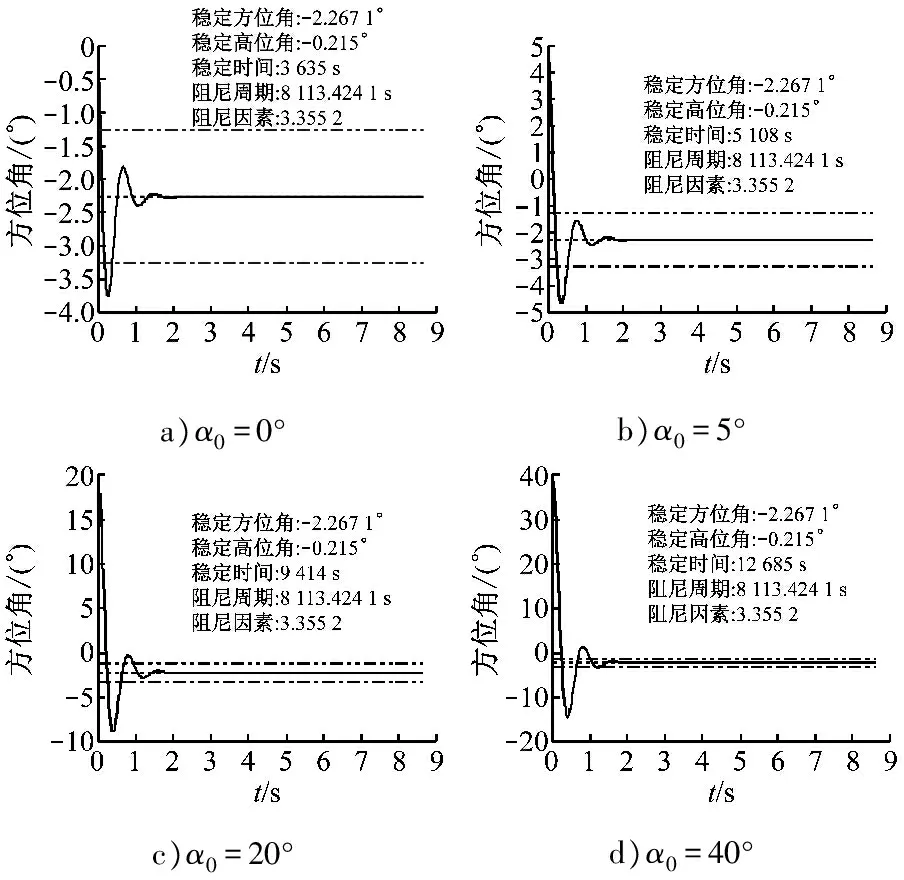
a)α0=0°b)α0=5°c)α0=20°d)α0=40°

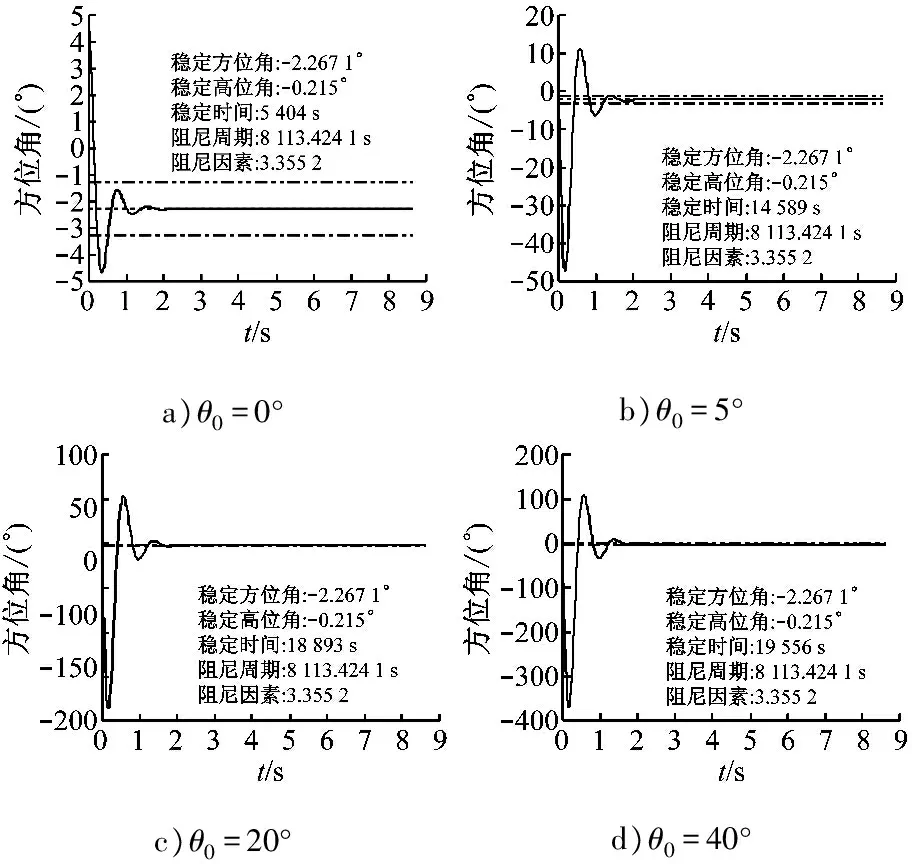
图4 仿真条件2下的方位角曲线

图5 仿真条件3下的方位角曲线

由以上分析可知：罗经稳定位置和阻尼周期与陀螺仪主轴初始指向没有关系；陀螺仪初始指向主要影响罗经稳定时间。

(1)当陀螺仪主轴初始高度角为5°时，初始方位角减小，稳定时间不一定缩短。初始方位角增大，稳定时间不一定延长。例如：在初始方位角为40°时，稳定时间为122 424 s；而在初始方位角为5°时，稳定时间为14 589 s。

(2)当陀螺仪主轴初始高度角为0°时，稳定时间随着初始方位角的减小而显著缩短。例如：在初始方位角为40°时，稳定时间为12 685 s；而在初始方位角为5°时，稳定时间为5 108 s，稳定时间缩短超过50%。

(3)当陀螺仪主轴初始方位角为5°时，稳定时间随着初始高度角的减小而缩短，但缩短的幅度较小。例如：在初始高度角为40°时，稳定时间为19 556 s；而在初始高度角为5°时，稳定时间却为14 589 s，稳定时间减小约25%。

以上罗经稳定参数与初始偏差角的变化关系见表3。

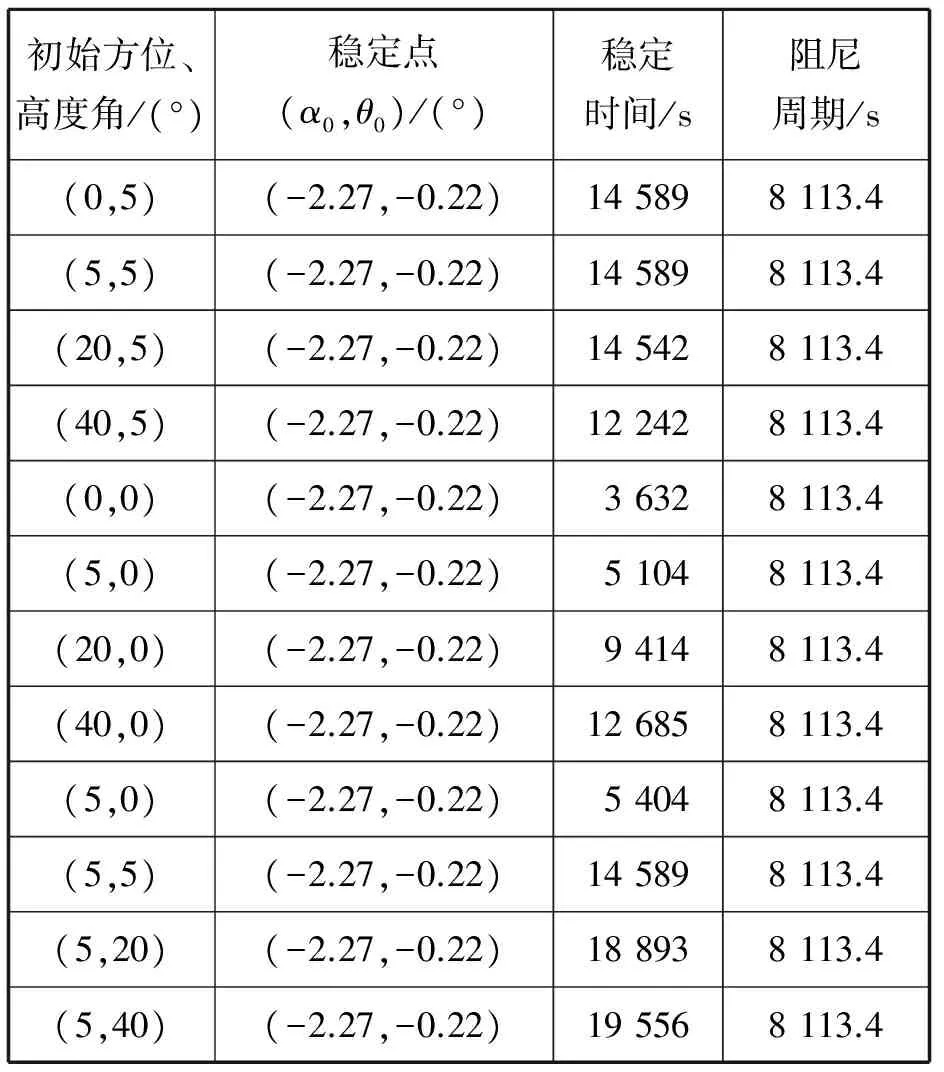
表3 罗经稳定参数与初始偏差角变化关系

4 结束语

电控陀螺罗经可为舰船提供航向信息，广泛应用在商船和军舰的航海导航中，稳定精度、稳定时间和阻尼周期是其3个关键性能参数。本文根据电控陀螺罗经的力矩方程推导出主轴运动方程，利用MATLAB Simulink建立罗经的仿真模型和流程，研究力矩系数变化、初始条件变化与罗经稳定过程之间的关系。综合分析仿真结果，可得到：

1)电控陀螺罗经的稳定精度随着纬度的升高而降低；稳定时间随着纬度的升高而显著延长。

2)通过改变找北力矩和阻尼力矩系数，可提高罗经的稳定性能。单独放大找北力矩，可提高罗经的稳定精度，但会显著延长稳定时间；单独放大阻尼力矩，可缩短稳定时间，但稳定精度会下降；同时放大找北力矩和阻尼力矩，可均衡稳定精度，并缩短稳定时间。

3)罗经的稳定精度和阻尼周期与陀螺仪主轴的初始方位角和高度角没有关系，初始方位角和高度角主要影响罗经的稳定时间。

4)在初始高度角不为0°的情况下，减小初始方位角不一定能缩短稳定时间，反而可能延长稳定时间；只有在初始高度角为0°的情况下，罗经稳定时间才会随着初始方位角的减小而显著缩短。

5)在初始方位角一定的情况下，减小初始高度角可小幅缩短稳定时间，但效果并不明显。

以上结论表明：根据陀螺罗经工作位置动态调整力矩系数，可有效缩短稳定时间，获得一定的稳定精度；陀螺罗经启动过程中，陀螺仪主轴应先调水平，然后找北，这样可大大缩短罗经稳定时间。为提高电控陀螺罗经的稳定性能，提高其高纬度位置的工作性能，可设计力矩系数自适应调节结构，设计调节主轴初始方位角和高度角的机构，并规定其工作流程为先水平后找北。

[1] 许江宁，边少锋，殷立吴.陀螺原理[M].北京：国防工业出版社,2005：125-156.

[2] 严普强，周兆英.电控陀螺罗经的机动误差及补偿方法[J].清华大学学报(自然科学版),1980,20(1):61-72.

[3] 翟羽健.电控陀螺罗经可靠性分析及评估[J].东南大学学报(自然科学版),1988,18(3):66-75.

[4] 施红兵，叶松柏，陆恺.状态自动切换法减小电控陀螺罗经机动误差的研究[J].上海交通大学学报,1989,23(6):84-90.

[5] 郝燕玲，张义，孙枫. 航向大失准角下的罗经法对准研究[J].仪器仪表学报,2011,32(7):1478-1484.

[6] 李汉舟，潘泉，邓麟，等. 极点配置对SINS罗经对准性能影响[J].中国惯性技术学报,2014,22(6):711-718.

[7] 徐博，陈春，郝燕玲，等.动基座捷联罗经初始对准误差分析[J].系统工程与电子技术,2013,35(4):812-819.

[8] 郝燕玲,张义,孙枫,等. 单轴旋转式捷联惯导方位对准研究[J].仪器仪表学报,2011,32(2):309-315.

[9] 徐定杰,宋鸿儒,张义.基于双系统思想的船用捷联罗经系统算法[J].华中科技大学学报(自然科学版),2013,41(1):85-88.

SimulationofNorth-SeekingProcessofElectricallyTorquedGyrocompass

YUANQunzhe，ZHOUHongjin，JIANGYongxin，HANYundong

(Department of Navigation, Dalian Naval Academy, Dalian 116018, China)

U666.151

A

2016-12-11

国家自然科学基金(41374018)；海军大连舰艇学院2110三期资助学术预研课题(2014007)

袁群哲(1964—)，男，浙江桐庐人，高级工程师，硕士，研究方向为导航制导与控制。E-mail：zhou_hongjin@126.com

1000-4653(2017)01-0004-04