基于马尔克夫灰色残差GM(1，1)模型的HTPB推进剂贮存寿命预估

杜永强，郑 坚，彭 威，张 晓，顾志旭，刘忠会

(1.军械工程学院，石家庄 050003；2.65185部队，铁岭 112611)

2015-12-08；

2016-09-05。

杜永强(1991—)，男，硕士生，研究方向为复合固体推进剂贮存老化性能及建模。E-maildyqangus@163.com

基于马尔克夫灰色残差GM(1，1)模型的HTPB推进剂贮存寿命预估

杜永强1，郑 坚1，彭 威1，张 晓1，顾志旭1，刘忠会2

(1.军械工程学院，石家庄 050003；2.65185部队，铁岭 112611)

针对Arrhenius方程将活化能假设与温度无关的常数，给HTPB(端羟基聚丁二烯)推进剂寿命预估引入了误差的问题，提出了基于马尔克夫灰色残差GM(1，1)模型的寿命预估方法。对HTPB推进剂进行了高温加速寿命试验，以最大延伸率作为性能变化表征参数，根据老化反应速率常数随温度的变化关系，建立了马尔克夫灰色残差GM(1,1)模型，对常温条件下推进剂的老化反应速率常数进行了预测，并预估了HTPB推进剂在常温条件下的贮存寿命为11.74 a。

HTPB推进剂；高温加速寿命试验；马尔克夫灰色残差GM(1,1)模型；寿命预估

0 引言

HTPB推进剂是一种以聚合物丁羟粘合剂为基体的并具有特定性能的含能复合材料，是火箭发动机的动力之源。在贮存过程中，由于受到复杂的物理、化学等因素的综合影响，导致推进剂的力学性能逐渐发生变化而达不到使用要求[1-2]。为防止推进剂提前退役造成的资源浪费和过期服役可能造成的危害，需要对HTPB推进剂的贮存寿命进行预估。目前常用的方法是将高温加速寿命试验和Arrhenius方程相结合，建立推进剂力学性能随贮存时间变化的老化模型，进而外推出常温贮存下的使用寿命[3]。但Arrhenius方程将活化能假设为与温度无关的常数，研究结果表明，活化能是反应温度的函数，在温度范围较大时，推进剂的反应活化能发生了改变，因而使用Arrhenius方程为推进剂的寿命预估引入了误差[4]。为提高寿命预估的精度，高大元等[5]提出了将Arrhenius方程修改为三参数公式，傅惠民等[6]在三参数公式的基础上提出了整体预测方法，在一定程度上减小了预估结果的误差。针对常温自然老化试验的样本点有限的问题，陈奎等[7]将考虑马尔克夫过程的灰色残差GM(1，1)模型引入到材料的老化行为预测当中。结果表明，该方法的预测精度较高，是一种可靠的老化行为预测方法。但该方法尚未用于HTPB推进剂的高温加速寿命试验当中，寿命预估结果的准确性还没有进行验证。

本文将考虑马尔克夫过程的灰色残差GM(1，1)模型应用于HTPB推进剂贮存寿命预估研究当中，对HTPB推进剂进行了高温加速寿命试验，以最大延伸率作为力学性能表征参数，通过修正老化起点和建立老化模型，对HTPB推进剂在常温下的贮存寿命进行了预估。为了验证模型的准确性，将引入马尔克夫过程的灰色残差GM(1，1)模型的贮存寿命预估结果与Arrhenius方法和常温外推试验方法进行了对比分析。

1 试验

1.1 试件的老化及测试

选取某型号哑铃型HTPB推进剂试件进行试验，将试件用铝塑袋密封包装，放入DU288型电热油浴恒温箱，参照GJB 770B—2005中506.1[8]的相关方法进行高温加速寿命试验。设置老化温度分别为(45±1)、(55±1)、(65±1)、(75±1)℃，控制老化箱内的湿度小于30%RH。老化后的试件在进行最大延伸率测试之前，首先在密闭的干燥器中自然冷却24 h，然后参照GJB 770B—2005中413.1[8]的方法，使用Instron 5982型材料拉伸机上测试试件的最大延伸率。记录试验数据，并绘制HTPB推进剂最大延伸率随贮存时间的变化曲线。采用洛马诺夫斯基准则(t检验准则)提出异常数据，选用正常的试验数据进行分析处理。

1.2 试验结果

图1为高温加速寿命试验推进剂最大延伸率随贮存时间的变化曲线。

由图1可看出，在4个老化温度下，HTPB推进剂最大延伸率随贮存时间变化曲线的趋势相同，说明4个温度下推进剂的老化机理相似，且随老化温度升高，推进剂的老化反应速率明显增加，这是因为高温条件加速了推进剂的老化反应进程。总体上来看，HTPB推进剂最大延伸率随贮存时间的增加呈现先快速下降后缓慢降低的趋势[9]。

2 建模及分析

2.1 老化起点的修正

由图1可看出，HTPB推进剂最大延伸率随贮存时间的变化曲线与老化的对数模型的趋势相同，故选取该模型进行分析：

εm=εm0+klgt

(1)

其中，εm为HTPB推进剂最大延伸率；εm0为常数；t为老化反应时间；k为老化反应速率常数，遵从Arrhenius方程[10]，且有：

k=Aexp(-E/RT)

(2)

其中，E为反应活化能，J/mol；A为指前因子；R为普适气体常数，J/(mol·K)。

在固化过程中，老化反应也在同时进行，因此固化终点并非老化起点。假设HTPB推进剂在温度T0下进行固化，加上固化前后的升降温时间，总共的固化时间为t0，则其他温度T下的对应时间由Arrhenius导出式进行修正：

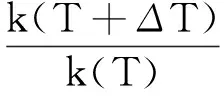
(3)

式中 ΔT=T0-T。

将推进剂的反应活化能代入式(3)，可求得不同温度T下k值与固化温度T0下的k值之比。假设固化结束后式(1)中(εm-εm0)为一定值，则可导出：

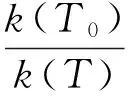
(4)

即可求出不同老化温度下的老化起点。

2.2 灰色残差GM(1，1)模型

设不同老化温度下的老化反应速率常数组成了序列K(0)，即K(0)={k(0)(1)，k(0)(2)，…，k(0)(n)}，可得一次累加序列K(1)，K(1)={k(1)(1)，k(1)(2)，…，k(1)(n)}，其中：

(5)

根据式(5)的计算结果，可得到序列K(1)的紧邻均值序列Z(1)，Z(1)={z(1)(2)，z(1)(3)，…，z(1)(n)}，其中：

z(1)(m)=1/2(x(1)(m)+x(1)(m-1))，

m=2，3，…，n

(6)

构建微分方程dK(1)/dt+aK(1)=b，其中，参数a、b可由式(7)得出：

[a，b]T=(BTB)-1BTY

(7)

对上述微分方程进行求解，可得灰色GM(1，1)模型如式(8)所示：

(8)

其还原值满足式(9)：

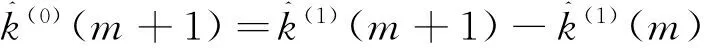
m=1，2，…，n

(9)

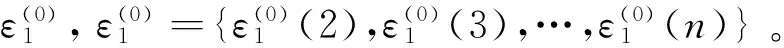
(10)

ε(0)={ε(0)(2)，ε(0)(3)，…，ε(0)(n)}

(11)

对得到的ε(0)按照式(5)～式(9)的步骤建立灰色GM(1，1)模型，可得：

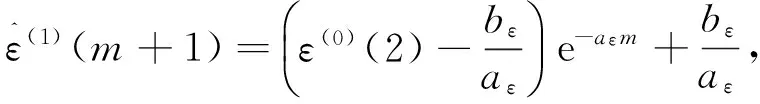
m=2，3，…，n

(12)

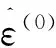
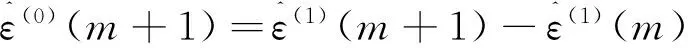
m=2，3，…，n

(13)

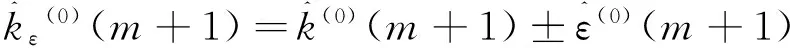
m=2，3，…，n

(14)

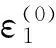
2.3 马尔克夫过程预测模型

灰色残差GM(1，1)模型可用于预测其他老化温度下推进剂的老化反应速率常数，但模型中预测的残差修正值的符号难以确定，采用马尔克夫过程预测模型，可有效解决这一问题[11]。

假设状态1表示残差为正值，状态2表示残差为负值，并确定初始状态向量为

(15)

根据残差序列的正负状态，求出状态转移概率矩阵P：

(16)

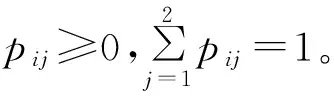
pij=sij/si，i=1，2；j=1，2

(17)

式中sij为状态i转移到状态j的次数；si为状态i出现的次数。

则灰色残差GM(1，1)模型预测的残差修正值在下一时刻t的状态转移结果s(t)为

s(t)=s(0)·P

(18)

以s(t)中概率大的状态作为时刻t时残差修正值的状态，即正负号。如果两者的概率相等，则取上一时刻残差修正值的状态作为该时刻的状态。

3 数据处理及寿命预估

本文所使用的HTPB推进剂在70 ℃条件下固化3 d，加上升降温的时间，总计为4 d。依据线性活化能法[12]，测得推进剂活化能为21.338×103J/mol，代入式(3)、式(4)中可得修正的老化起点，如表1所示。

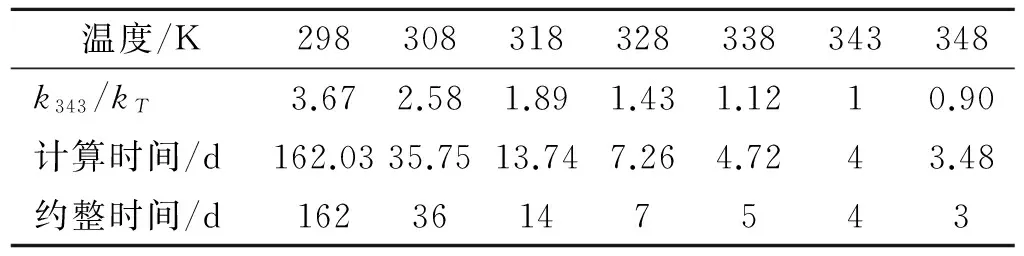
表1 修正的老化起点

将4个温度下高温加速寿命试验结果代入式(1)中，借助MATLAB工具做线性拟合，并进行相关性分析，结果如表2所示。其中，r为相关性系数，r0.01为显著性水平为0.01时的临界相关系数，n为样本点数。

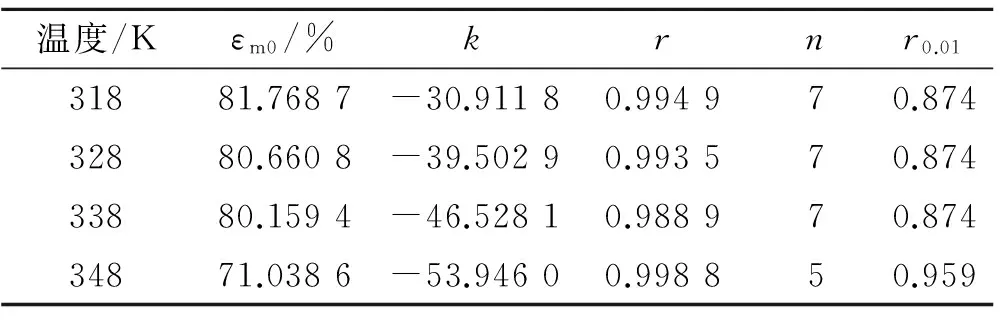
表2 参数拟合及相关性分析

由表2分析结果可得出，对数模型的相关系数均大于0.98，说明选择对数模型进行数据处理相关性水平较高。将表2中不同老化温度下的老化反应速率常数按照2.2节和2.3节中的方法，建立灰色残差GM(1，1)模型进行模拟和预测结果，并引入马尔克夫过程预测模型预测残差的正负值，结果见表3和表4。

由表3结果可知，灰色残差GM(1，1)模型的模拟结果与实际值的相对误差很小，说明该模型可用于老化反应速率常数的模拟和预测中。表4中采用马尔克夫过程的预测模型预测得到残差模拟值的符号均为负值，最终计算得到常温25 ℃(298 K)条件下HTPB推进剂的老化反应速率常数为21.092 6。

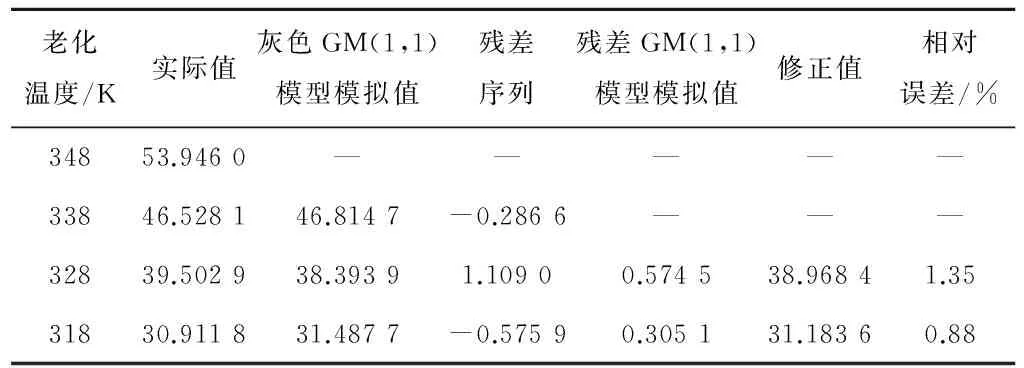
表3 老化反应速率常数模拟结果

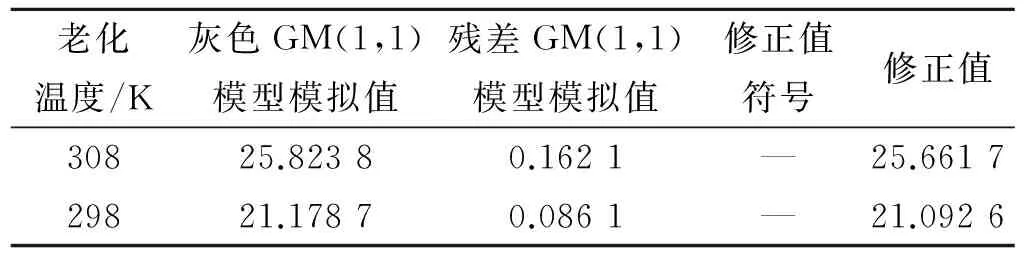
表4 老化反应速率常数预测结果

由表1老化起点的修正结果可知，在常温25 ℃条件下HTPB推进剂的老化起点为162 d，最大延伸率初始值为45.7%，将此时预测得到的老化反应速率常数代入式(1)中可得：εm0=45.7+21.092 6×lg(162)=92.304 4，则常温25 ℃条件下的老化模型为

εm=92.304 4-21.092 6lgt

(19)

以最大延伸率下降30%为失效判据，预估HTPB推进剂在常温25 ℃条件下的贮存寿命为4.283 5×103d，即11.74 a。

为验证模型预估寿命结果的准确性，将该模型与传统Arrhenius方法和常温外推试验方法进行对比分析，结果如表5所示。

表5 模型对比分析结果

由表5可得出，传统Arrhenius方法得到的老化反应速率常数低于考虑马尔克夫过程的灰色残差GM(1，1)模型的结果，预估得到的HTPB推进剂在常温下的贮存寿命要大于常温外推结果，且相对误差较大，预估的精度不高；灰色残差GM(1，1)模型的预估结果和常温外推试验结果相比，误差只有5.06%，在误差允许的范围内，可以对HTPB推进剂的贮存寿命进行有效预估。

4 结论

(1)通过结合Arrhenius方程导出式和对数模型，对HTPB推进剂高温加速寿命试验的老化起点进行了修正，确保老化试验结果与实际贮存相符合。

(2)借助灰色残差GM(1，1)模型对HTPB推进剂在常温25 ℃条件下的老化反应速率常数进行了预测，并引入马尔克夫过程预测模型确定残差修正值的符号，从而得到修正后的老化反应速率常数结果，运用该结果预估HTPB推进剂在常温25 ℃条件下的贮存寿命为11.735 6 a，该预估寿命和常温外推试验结果相比误差为5.06%，且小于传统Arrhenius方法，验证该模型可对HTPB推进剂的贮存寿命进行有效预估。

[1] 侯林法.复合固体推进剂[M].北京:中国宇航出版社,1994:1-2.

[2] 庞爱民.固体火箭推进剂理论与工程[M].北京:中国宇航出版社,2014:129-139.

[3] Huang W,Duane L.An alternative degradation reliability modeling approach using maximum likelihood estimation [J].IEEE Transactions on Reliability,2005,54(2):310-317.

[4] 杨根,赵永俊,张炜,等.HTPB推进剂贮存期预估模型研究[J].固体火箭技术,2006,29(4):283-285.

[5] 高大元,何碧,何松伟,等.Arrhenius方法的局限性讨论[J].含能材料,2006,14(2):132-135.

[6] 傅惠民,杨立保,林逢春,等.固体推进剂贮存寿命整体预测方法[J].机械强度,2007,29(5):754-759.

[7] 陈奎,张天云,卢柏林,等.基于马尔克夫的灰色残差GM(1,1)模型在塑料老化行为预测中的应用[J].重庆大学学报,2014,37(5):71-76.

[8] GJB 770B—2005.火药试验方法[S].2005.

[9] 张兴高.HTPB推进剂贮存老化特性及寿命预估研究[D].长沙:国防科技大学,2009.

[10] 胡荣祖,史启祯.热分析动力学[M].北京:科学出版社,2001.

[11] 王翠茹,孙辰军,杨静,等.改进残差灰色预测模型在负载预测中的应用[J].电力系统及其自动化学报,2006,18(1):86-89.

[12] 张昊,罗怀德,杜鹃.线性活化能法预估推进剂贮存寿命研究[J].固体火箭技术,2002,25(2):56-58.

Shelf-lifepredictionforHTPBpropellantbasedonaMarkovgreyresidualGM(1，1)model

DU Yong-qiang1，ZHENG Jian1，PENG Wei1，ZHANG Xiao1，GU Zhi-xu1，LIU Zhong-hui2

(1.Ordnance Engineering College，Shijiazhuang 050003，China；2.Unit 65185，Tieling 112611，China)

To solve the problem that the activation energy is assumed to be independent of temperature in the Arrhenius equation, which introduces error to the shelf-life prediction of HTPB propellant,the storage life prediction method was proposed based on Markov grey residual GM(1，1)model.The high temperature accelerated life test of HTPB propellant was carried out,and the maximum elongation was used as the characteristic parameter.According to the relationship between the aging reaction rate constant with temperature change,the Markov grey residual GM(1，1)model was established.The aging reaction rate constant of propellant under room temperature was predicted,and the storage life of HTPB propellant under room temperature condition was estimated for 11.74 years.

HTPB propellant；high temperature accelerated life test；Markov GM(1，1)model；life prediction

V512

A

1006-2793(2017)05-0588-04

10.7673/j.issn.1006-2793.2017.05.009

(编辑：刘红利)