The Expression of Slow-growing Meromorphic Functions Sharing One Value CM with Their Derivatives

XU AI-zHUAND CHEN SHENG-jIANG

(1.Department of Mathematics,Ningde Normal University,Ningde,Fujian,352100)

(2.Department of Mathematics,Fujian Normal University,Fuzhou,350007)

The Expression of Slow-growing Meromorphic Functions Sharing One Value CM with Their Derivatives

XU AI-zHU1AND CHEN SHENG-jIANG2,*

(1.Department of Mathematics,Ningde Normal University,Ningde,Fujian,352100)

(2.Department of Mathematics,Fujian Normal University,Fuzhou,350007)

Communicated by Ji You-qing

In this paper,we study the relations between meromorphic functions and their derivatives with one shared values,and obtain a concrete expression of meromorphic functions of zero order that share one value CM with their derivatives by a new method.Our main result is the supplementary of a related result due to Li and Yi(Li X M,Yi H X.Uniqueness of meromorphic functions sharing a meromorphic function of a small order with their derivatives.Ann.Polon.Math.,2010,98(3):201–219).

meromorphic,derivative,shared value

1 Introduction and Main Results

A meromorphic function always mean meromorphic in the whole complex plane in this paper.We say that two meromorphic functions f(z)and g(z)share a finite value a IM(ignoring multiplicities)provided that f−a and g−a have the same zeros.If f−a and g−a have the same zeros with the same multiplicities,then we say f(z)and g(z)share the value a CM(counting multiplicities).We assume that the reader is familiar with the fundamental concepts of Nevanlinna’s value distribution theory,e.g.,[1]and[2],and in particular with the most usual of its symbols:m(r,f),N(r,f),T(r,f)and so on.

Br¨uck[3]seems to be the first one who considered the relations between meromorphicfunctions and their derivatives concerning one shared value,and presented the following well-known conjecture in 1996.

Bru¨ck[3]showed that the conjecture is true when a=0,and Gundersen and Yang[4]proved the case that f is of finite order.The case ρ(f)=∞andwas be proved by Chen and Shou[5],where

Although the Br¨uck’s Conjecture is still open by now,it has induced many papers to investigate the related uniqueness problems which are analogue to this conjecture.

In 1999,Yang[6]proved the following result.

Theorem 1.1[6]Let f be a nonconstant entire function of finite order,a be a finite nonzero constant,and k be a positive integer.If f and f(k)share a CM,then f(k)−a=c(f−a)for some nonzero complex number c.

Chang and Zhu[7]replaced the shared-value by a meromorphic function and proved the next result.

Theorem 1.2[7]Let f and a be two meromorphic functions such that f and a have finitely many poles,and such that f and a have no common poles.If f−a and f′−a share 0 CM,and if ρ(a)＜ρ(f)＜∞,then f′−a=c(f−a)for some nonzero constant c.

Later,Li and Yi[8]improved Theorem 1.2 to the next result.

Theorem 1.3([8],Theorem 1.2)Let f and a(/≡0)be two meromorphic functions such that f and a have finitely many poles,and such that f and a have no common poles.If ρ(a)＜ρ(f)＜∞and if f−a and f(k)−a share 0 CM,where k(≥1)is an integer,then f(k)−a=c(f−a)for some nonzero constant c.

In[7]and[8],the authors showed by an example that the condition“ρ(a)＜ρ(f)”cannot be replaced by“ρ(a)=ρ(f)”.Let f(z)=e2z−(z−1)ezand a(z)=e2z−zez.Then we can verify that f−a and f′−a share 0 CM and f′−a=ez(f−a).

However,by an obvious observation,we can find that the order of f in Theorems 1.2 and 1.3 is strictly greater than 0.Thus,it is interesting to ask:

Question 1.1Suppose that f is a meromorphic function with at most finitely many poles such that ρ(f)=0.What can be said if f and f(k)share a finite nonzero complex value a CM?

A special case of the above question is of rational functions.For this case,Li and Yi proved the following result in[8].

Theorem 1.4([8],Theorem 1.3)Let f be a nonconstant rational function,and a be a nonzero finite complex number.If f and f(k)share a CM,where k(≥1)is a positive integer,

then

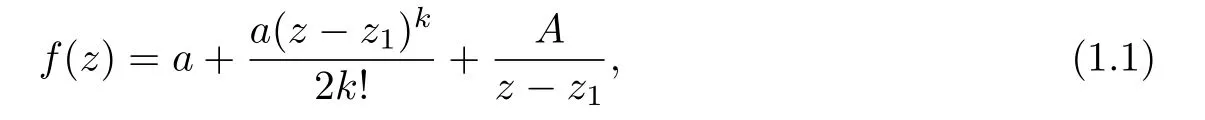
where z1and A(/=0)are two complex numbers.

Unfortunately,the assertion of Theorem 1.4 is incomplete.We give two examples to illustrate this point.

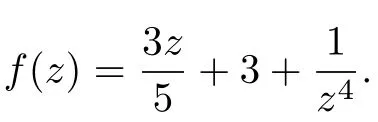
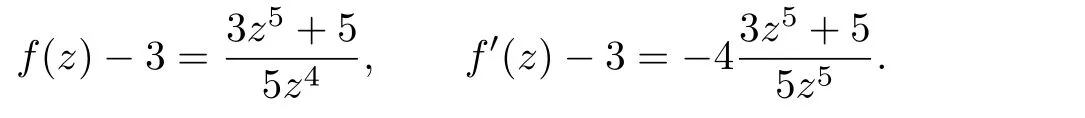
Thus,f(z)and f′(z)share 3 CM.But f(z)does not satisfy the form(1.1).

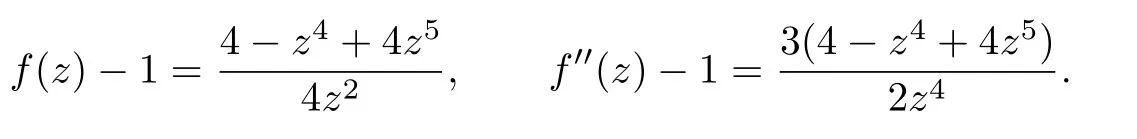
Hence,f(z)and f′′(z)share 1 CM.But f(z)does not satisfy the form(1.1).

In this paper,we prove the following result with respect to the above question.

Theorem 1.5Let f be a nonconstant meromorphic function with at most finitely many poles,a be a finite complex number,and k be a positive integer.Suppose that ρ(f)=0.If f and f(k)share a CM,then f assumes the form:

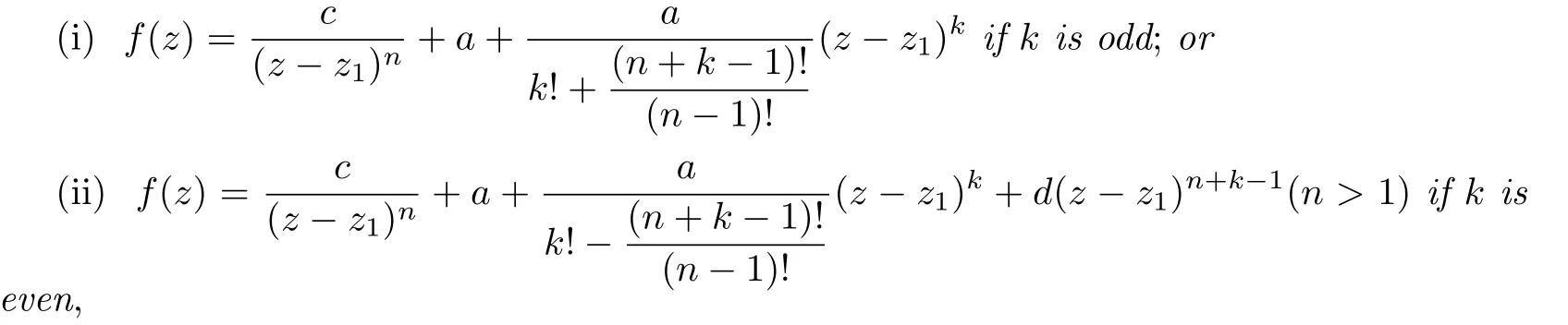
where z1,c(/=0)and d are complex numbers,n is some positive integer.

The above Examples 1.1 and 1.2 show that the conclusions of Theorem 1.5 could occur.From Theorems 1.2 and 1.5 we have

Corollary 1.1Let f be a nonconstant meromorphic function of finite order such that f has at most finitely many poles,and a be a finite nonzero complex number.If f and f′share a CM,then one and only one of the following conclusions holds:

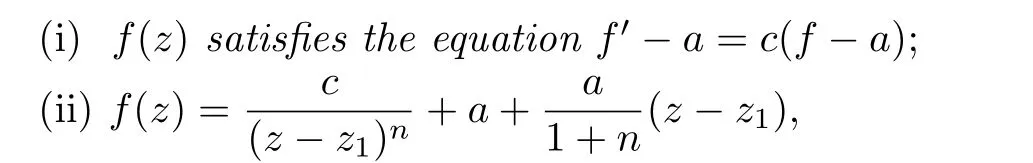
where c(/=0)and z1are two complex numbers.

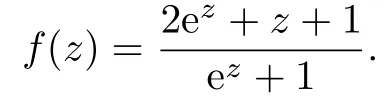
2 Some Lemmas

To prove our result,we recall the following results.

Lemma 2.1[2]Suppose that f1,f2,···,fn(n≥2)are meromorphic functions and g1,g2,···,gnare entire functions satisfying the following conditions:

(ii)gj(z)−gk(z)are not constants for 1≤j＜k≤n;

(iii)For 1≤j≤n,1≤h＜k≤n,T(r,fj)=(r→∞,r/∈E,measE＜∞).

Then fj≡0(j=1,2,···,n).

Lemma 2.2[2]Let f(z)be a nonconstant meromorphic function.If f has Picard values 0 and∞,then f(z)=eh(z),where h(z)is an entire function.

3 Proof of Theorem 1.5

We consider the following two cases.

Case 1.f(z)has no pole.

Since f and f(k)share a CM,according to Lemma 2.2 we have

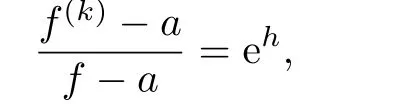
where h is an entire function.Since ρ(f)=0,it follows that ρ(f(k))=0 and hence ehis a nonzero constant,saying c,that is,

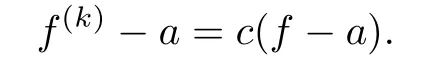
Thus,f assumes the form

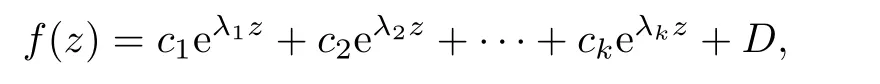
Case 2.f(z)has at least one pole.

By the assumptions of Theorem 1.5,we may assume that f has q≥1 distinct poles z1,z2,···,zqwith multiplicities k1,k2,···,kq,respectively.

Since f and f(k)share a CM,we can deduce from Lemma 2.2 that

where G(z)=(z−z1)(z−z2)···(z−zq)and α is an entire function.Noting ρ(f(k))=ρ(f)=0,we know that α is a constant.Thus,we have

where A1,···,Aqare q nonzero constants.For each zj(j=1,2,···,q),we could assume that the Laurent expansion of f(z)near zjis

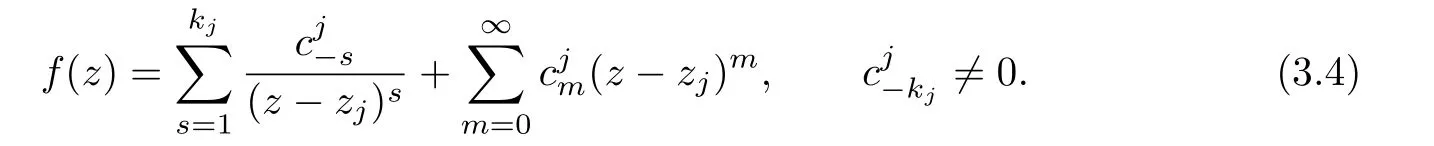
By a simple calculation,we have

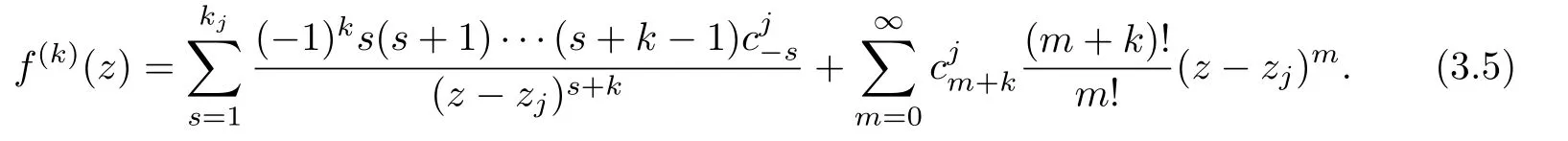
By substituting(3.4)and(3.5)into the left hand side of(3.2),and substituting(3.3)into the right hand side of(3.2),respectively,we have

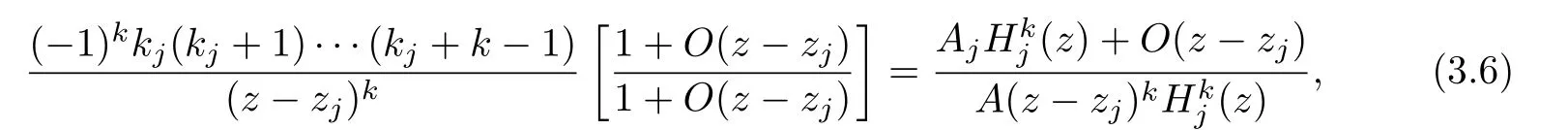
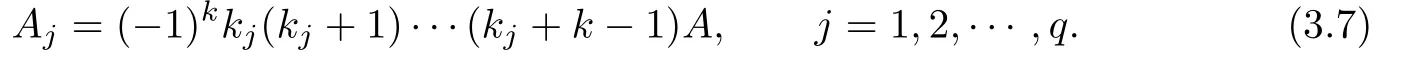
If q≥2,it follows from(3.3)immediately that due to(3.7).But this is impossible.So,we have q=1.

For the sake of simple,we replaceand k1by cjand n in above notations respectively.

Now,we can rewrite(3.2)as

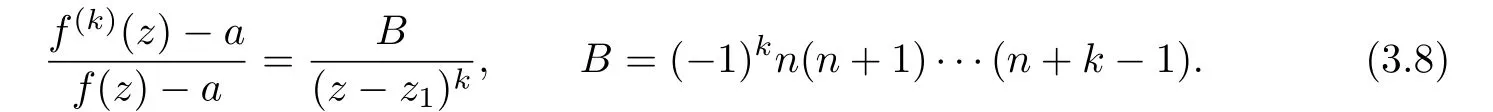
Combining(3.4),(3.5)and(3.8),we have

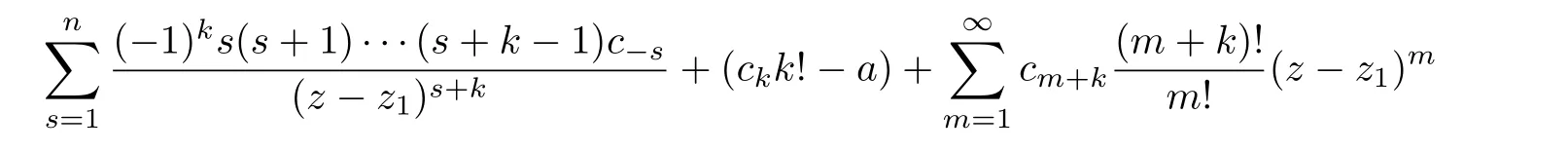
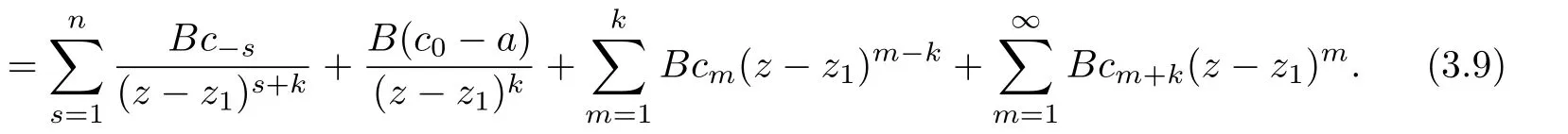
Next,we consider the following two subcases.

Subcase 2.1.k is odd.

Then,by the uniqueness of the coefficients of Laurent expansion in(3.9),we have

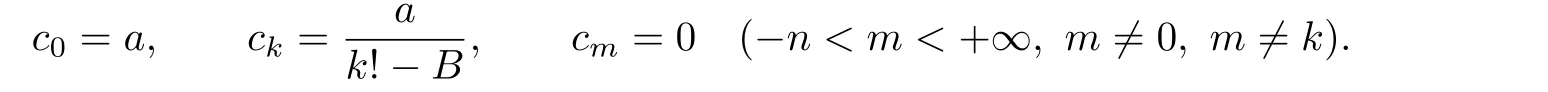
Hence,f(z)has the form

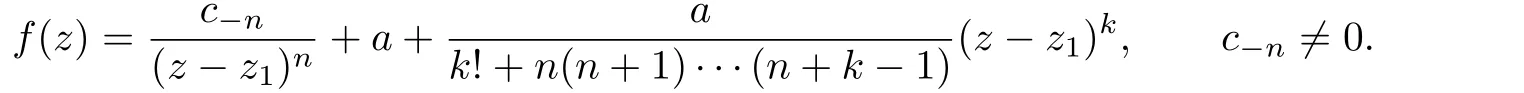
Subcase 2.2.k is even.

By using the same arguments as the proof of subcase 2.1,we have

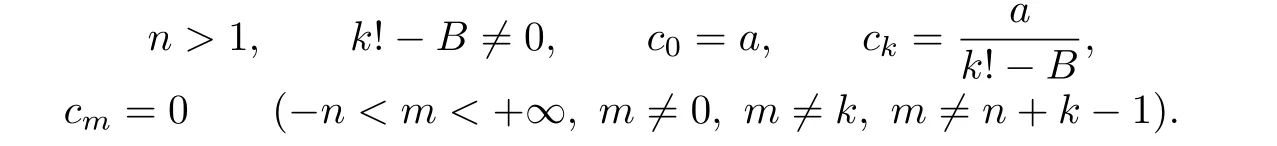
Hence,f(z)has the form

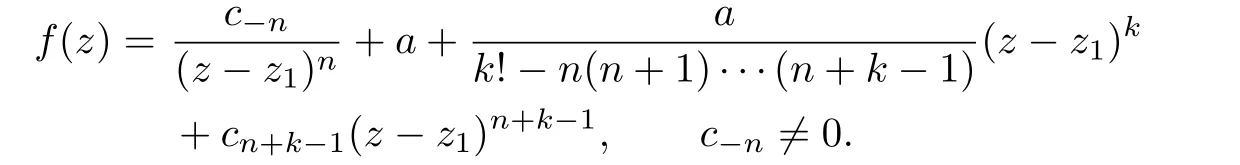
This completes the proof of Theorem 1.5.

[1]Hayman W K.Meromorphic Functions.Oxford:Clarendon Press,1964.

[2]Yang C C,Yi H X.Uniqueness Theory of Meromorphic Function.Dordrecht:Kluwer Academic Publishers,2003.

[3]Br¨uck R.On entire functions which share one value CM with their first derivative.Results Math.,1996,30(1):21–24.

[4]Gundersen G,Yang L Z.Entire functions that share one value with one or two of their derivatives.J.Math.Anal.Appl.,1998,223(1):88–95.

[5]Chen Z X,Shon K H.On conjecture of R.Br¨uck concerning the entire function sharing one value CM with its derivative.Taiwanese J.Math.,2004,8(2):235–244.

[6]Yang L Z.Solution of a differential equation and its application.Kodai Math.J.,1999,22(3):458–464.

[7]Chang J M,Zhu Y Z.Entire functions that share a small function with their derivatives.J.Math.Anal.Appl.,2009,351(1):491–496.

[8]Li X M,Yi H X.Uniqueness of meromorphic functions sharing a meromorphic function of a small order with their derivatives.Ann.Polon.Math.,2010,98(3):201–219.

30D35

A

1674-5647(2017)04-0377-06

10.13447/j.1674-5647.2017.04.10

date:April 8,2017.

The NSF(11301076)of China,the NSF(2014J01004)of Fujian Province,the SRP(JA15562)of Fujian Provincial Education Department,and the Foundation(2014Q64)of NDNU.

*Corresponding author.

E-mail address:xuaizhu@126.com(Xu A Z),ndsycsj@126.com(Chen S J).