On the Structure of the Augmentation Quotient Group for Some Non-abelian p-groups

ZHAO HUI-FANGAND NAN JI-zHU

(1.Police Technology Department,Railway Police College,Zhengzhou,450053)

(2.School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)

On the Structure of the Augmentation Quotient Group for Some Non-abelian p-groups

ZHAO HUI-FANG1AND NAN JI-zHU2,*

(1.Police Technology Department,Railway Police College,Zhengzhou,450053)

(2.School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)

Communicated by Du Xian-kun

In this paper,we study the basis of augmentation ideals and the quotient groups of finite non-abelian p-group which has a cyclic subgroup of index p,where pis an odd prime,and k is greater than or equal to 3.A concrete basis for the augmentation ideal is obtained and then the structure of its quotient groups can be determined.

integral group ring,augmentation ideal,quotient group,p-group

1 Introduction

The problem of determining the structure of augmentation ideals Δn(G)and quotient groups Qn(G)is an interesting topic in group ring theory.For abelian groups many works have been done(see[1]–[6]).In[2],Hales and Passi(see also[3])proved that for a finite abelian group G,there exists a number N such that for all n≥N,Qn(G)is isomorphic to QN(G).However,it is usually difficult to write down explicitly a basis of Δn(G)for an arbitrary finite non-abelian group,even for the non-abelian p-group.

For non-abelian finite p-group,if p=2 and every positive integer k is greater than or equal to 4,then there are exactly four isomorphism classes of non-abelian groups of order 2kwhich have a cyclic subgroup of index 2.The structure of augmentation quotient groups of all of which are well established,the dihedral group(see[7]),the generalized quaternion group(see[8]),the semidihedral group(or the quasidihedral group)and Mk(2)(see[9]).

If p/=2 and every positive integer k is greater than or equal to 3,then there is just one isomorphism class of non-abelian groups of order pkwhich have a cyclic subgroup of index p.Its presentation is given as follows:

We denote it by M.The current paper investigates the structure of the augmentation ideal and quotient group of the non-abelian p-group M.We prove that for n≥N=(p−1)k+1,

We start with some known results.In[4],Parmenter proved the following theorem.

Theorem 1.1Let G=〈g〉be cyclic of order m.Then the set

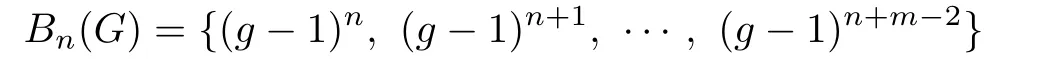
is a Z-basis for Δn(G).

Let G be a finite group,and denote by G1=[G,G]the commutator subgroup of G.For i≥1,define Gi=[G,Gi−1].Then we have the sequence:G=G0▷G1▷G2▷···.In[8],Zhou and You gave the following theorem.

Theorem 1.2g−1∈Δi+1(G),if g∈Gi.

2 Structure of Qn(M)for the Non-abelian p-group M

Let

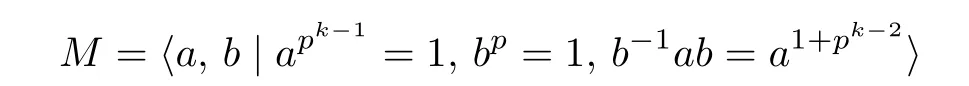
be a finite non-abelian p-group of order pkwhich have a cyclic subgroup of index p,where p/=2,k≥3.It is not hard to see that

and

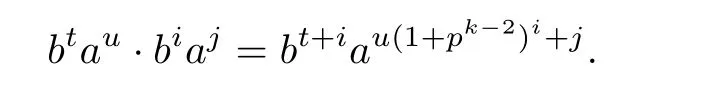
Consequently,we have

Lemma 2.1and for i≥2,one has Mi={1}.

Proof.By the definition of the group M,one has

Moreover,

The proof is completed.

Now by using Theorem 1.2,Lemma 2.1 and the formula

we have the following lemma.

Lemma 2.2pk−2(a−1)∈Δ2(M).

Lemma 2.3For t≥0,pt(b−1)∈Δ(p−1)t+1(M).

Proof.We give the proof by induction on t.If t=0,the equation is trivial.For t=1,since

we have

It follows that p(b−1)∈Δi(M)for i≤p.

Suppose that the conclusion is true for t.By induction,we obtain

as desired.The proof is completed.

Recall that the nth power Δn(M)of Δ(M)is a free Z-module of rank|M|−1 for any n≥1,and is generated as an abelian group by the products

where M={btau|0≤t≤p−1,0≤u≤pk−1−1}is the non-abelian p-group of order pk(k≥3)which have a cyclic subgroup of index p andThe recurrence relation of Δn(M)is given as follows.

Lemma 2.4Δ2(M)=Δ(〈b〉)(b−1)+Δ(M)(a−1)+pk−2(a−1)Z.Moreover,if n≥2,then

Proof.Since Δn(M)is generated by those elements as{(x1−1)···(xn−1)|xi∈M}with

for any i≥1,we have

If j≥1,we have

(i)If i/=0 or j＞1,by Lemmas 2.2 and 2.3,for any n,we have

(ii)If i=0 and j=1,then

i.e.,n=1.

If j=0,we prove it by induction on i.Remember that

and

then for i=n,

For n+1≤i≤n+p−1,notice that n≤i−1≤n+p−2,so

For i=n+p,one has

Assume that the conclusion is true for integer less than i≥n+p+1.Set i=n+p+t,where t≥1.Then by induction,we obtain

Hence,for n≥2,we have

and

Theorem 2.1Let Bn(M)denote a Z-basis for Δn(M).Then we have the following conclusions:

(I)For n=1,

(II)For 2≤n≤p,

(III)For n=(p−1)t+1 with 1≤t≤k−1,

(IV)For n=(p−1)t+s with 1≤t≤k−2 and 2≤s≤p,

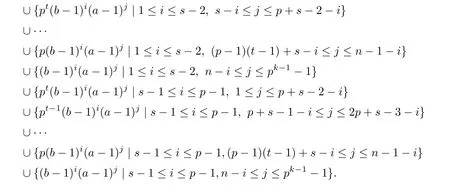
(V)For n=(p−1)(k−1)+s with 2≤s≤p,

(VI)For n=(p−1)(k−1)+s with s≥p,

Theorem 2.2Let M be the non-abelian p-group of order pk(p/=2,k≥3).

(i)If 2≤n≤(p−1)k,then

and

(ii)If n≥(p−1)k+1,then

Proof.(i)It is easy to see thatis a basis for Q1(M),and for 2≤n≤p−1,

is a set of basis for Qn(M).

is a set of basis for Qn(M).

is a set of basis for Qn(M).

is a set of basis for Qn(M).

By Lemmas 2.2 and 2.3,we get the conclusion.

3 Proof of Theorem 2.1

In order to prove Theorem 2.1,we need some lemmas as follows.

Note that we can obtain

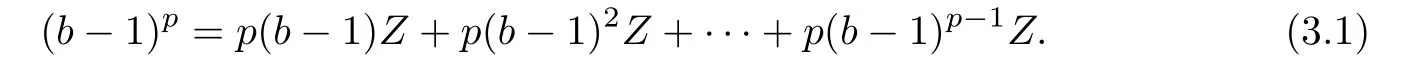
From equation(2.2)iteratively we also have

In fact,for the general case,we have

Lemma 3.1For t≥1,one has

Proof.We give the proof by induction on t.For t=1,it is obvious by(3.1).Suppose that it is true for t.Then by the inductive hypothesis and the above statement we have

Lemma 3.2For(p−1)(t−1)+1≤u≤(p−1)t with t≥1,pk+t−1(a−1)can be generated by

Proof.Note that if v=pjw and(w,p)=1,then

l is an integer.So,by the equality

we have

Then,for any u∈N+,u≥2,we have

By(3.2)and(3.3),we have

So for 2≤u≤p−1,we have

Then we get our conclusion for 2≤u≤p−1,that is to say,

Next we prove the result is true for p≤u≤2p−2.According to(3.3)and(3.4),we have

Multiplying both sides of the above equality by p,we have

Using the same method as above,we deduce that for p≤u≤2p−2,

Iteratively,we can obtain that if(p−1)(t−1)+1≤u≤(p−1)t,then

as desired.

Notice that from Theorem 1.1 we have

Now we can give the proof of Theorem 2.1.

Proof of Theorem 2.1We give the proof by induction on n≥1.

(I)n=1.It is obvious by(2.3),(2.4)and the definition of the augmentation ideal.

(II)2≤n≤p.For n=2,by Lemma 2.4,we have

Since

it follows that

Assume that the result is true for n(2≤n≤p−1).Then by(3.5)and Lemma 2.4,we have

since by Lemma 3.1,

That means Bn+1(M)is a set of Z-generators for Δn+1(M).

Direct computation shows

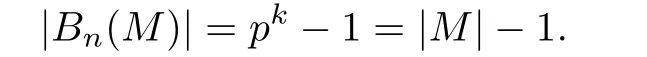
By Theorem 1.1,Bn(M)is a linearly independent set.Therefore,Bn(M)is a set of Z-basis for Δn(M).

(III)By the above result we have known that the conclusion is true for n=p=(p−1)×1+1.Suppose that it is true for n=(p−1)t+1,where 1≤t≤k−1.Then by(3.5)and Lemma 2.4,one has

By Lemma 3.1,we have

So Bn+1(M)is a set of Z-generators for Δn+1(M).Similarly to(II),we know that Bn(M)is a set of Z-basis for Δn(M).

(IV)Let n=(p−1)t+s,where 1≤t≤k−2,2≤s≤p−1.The result is true for(p−1)t+2 by(III).Assume that it is true for n.Then by(3.5)and Lemma 2.4,we have

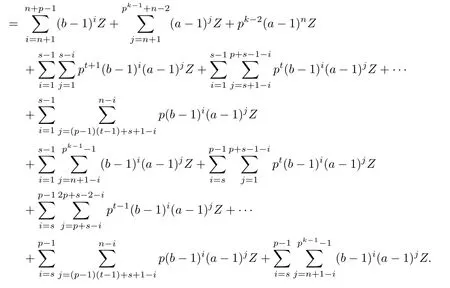
Again by Lemma 3.1,we have

So Bn+1(M)is a set of Z-generators for Δn+1(M).Similarly to(II),we know that Bn(M)is a set of Z-basis for Δn(M).

(V)By(IV)we know that the result is true for n=(p−1)(k−1)+2.Assume that the result is true for n=(p−1)(k−1)+s,2≤s≤p−1.Then by(3.5)and Lemma 2.4,we have

By Lemmas 3.1 and 3.2,we have

Moreover,pk(b−1)i(a−1)(1≤i≤s−1)can be generated by

So Bn+1(M)is a set of Z-generators for Δn+1(M).Similarly to(II),we know that Bn(M)is a set of Z-basis for Δn(M).

(VI)Assume that the result is true for n=(p−1)(k−1)+s,s≥p.Then by(3.5)and Lemma 2.4,we have

By Lemmas 3.1 and 3.2,for n≤m≤n+p−2,(b−1)m(a−1)can be generated by{pµ(b−1)i(a−1)Z|µ≥k,1≤i≤p−1},and pµ(b−1)i(a−1)can be generated by(3.6).So Bn+1(M)is a set of Z-generators for Δn+1(M).Similarly to(II),we know that Bn(M)is a set of Z-basis for Δn(M).

[1]Passi I B S.Group Rings and Their Augmentation Ideals.Lecture Notes in Mathematics,Vol.715.Berlin:Springer-Verlag,1979.

[2]Hales A W,Passi I B S.The augmentation quotients of finite Abelian p-groups.Contemp.Math.,1989,93:167–171.

[3]Bachman F,Grunenfelder L.The periodicity in the graded ring associated with an integral group ring.J.Pure Appl.Algebra,1974,5:253–264.

[4]Parmenter M M.A basis for powers of the augmentation ideal.Algebra Colloq.,2001,8(2):121–128.

[5]Tang G P.On a problem of Karpilovsky.Algebra Colloq.,2003,10(1):11–16.

[6]Bak A,Tang G P.Solution to the presentation problem for powers of the augmentation ideal of torsion free and torsion abelian groups.Adv.Math.,2004,189:1–37.

[7]Zhao H M,Tang G P.On the structure of augmentation quotient groups for some non-abelian groups.Adv.Math.,2008,37(2):163–170.

[8]Zhou Q X,You H.On the structure of augmentation quotient groups for generalized quaternion group.Algebra Colloq.,2012,19(1):137–148.

[9]Nan J Z,Zhao H F.On the structure of the augmentation quotient group for some non-abelian 2-groups.Czechoslovak Math.J.,2012,62(1):279–292.

16S34,20C05

A

1674-5647(2017)04-0289-15

10.13447/j.1674-5647.2017.04.01

date:May 6,2016.

The NSF(11371343,11461047)of China.

*Corresponding author.

E-mail address:zhf3002@163.com(Zhao H F),jznan@163.com(Nan J Z).