A Note on a Functional differential Equation with State Dependent Argument

ZHAO HOU-YU

(School of Mathematics,Chongqing Normal University,Chongqing,401331)

A Note on a Functional differential Equation with State Dependent Argument

ZHAO HOU-YU

(School of Mathematics,Chongqing Normal University,Chongqing,401331)

Communicated by Li Yong

This paper is concerned with solutions of a functional differential equation.Using Krasnoselskii’s fixed point theorem,the solutions can be obtained from periodic solutions of a companion equation.

iterative functional differential equation,periodic solution, fixed point theorem

1 Introduction

Recently,iterative functional differential equations of the form

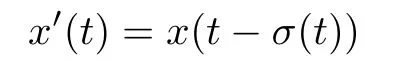
has appeared in several papers.However,such equations,about the periodic solution of the delay function σ(t)depends on the argument of the unknown function have been relatively little researched.McKiernan[1]considered analytic solutions of the problem

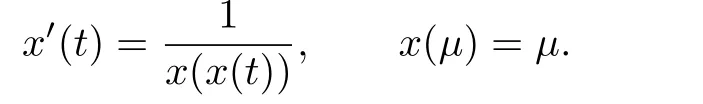
In[2]–[4],the authors studied the equations

andestablished sufficient conditions for the existence of analytic solutions in some local neighbourhoods of the fixed points of the functions.

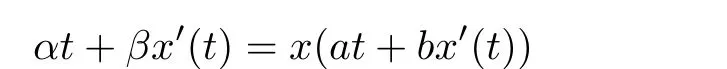
Since Burton[5]applied Krasnoselskii’s fixed theorem to prove the existence of periodic solutions,and this theorem has been extensively used in proving stability,periodic of solutions and boundedness of solutions in functional differential(Difference)equations.2005,Raffoul[6]used fixed point theorem to show a nonlinear neutral system

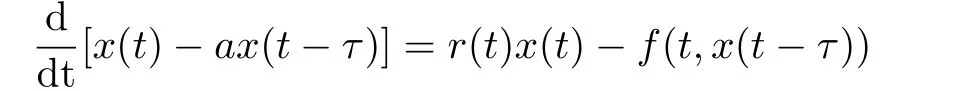
has a periodic solution.In[7],Guo and Yu discussed the existence and multiplicity of periodic of the second order Difference equation.Some other works can also be found in[8]–[12].

In this note,we show the solutions of equation(1.1)have a relation with a periodic function.In fact,letting

(1.1)can be changed into

Under certain conditions,we can find the equation(1.2)has periodic solutions y(t),and the solutions for the original equation can be obtained.

For convenience,we make use C(R,R)to denote the set of all real valued continuous functions from R into R.For T＞0,define

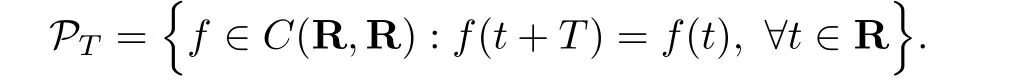
Then PTis a Banach space with the norm

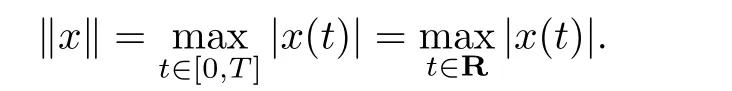
For P,L≥0,define the set

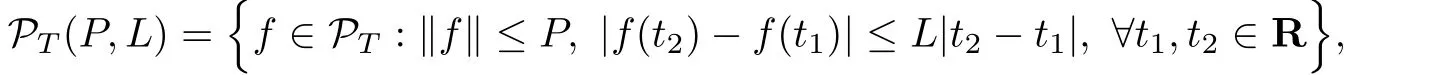
which is a closed convex and bounded subset of PT,and we wish to find T-periodic functions y∈PT(P,L)satis fies(1.2).

2 Periodic Solutions of(1.2)

In this section,the existence of periodic solutions of the equation(1.2)is proved.Now let us state the Krasnoselskii’s fixed point theorem,it is used to prove our main theorem.

Theorem 2.1[13]Let Ω be a closed convex nonempty subset of a Banach space(B,‖·‖).Suppose that A and B map Ω into B such that

(i)A is compact and continuous;

(ii)B is a contraction mapping;

(iii)x,y∈Ω implies Ax+By∈Ω.

Then there exists a z∈Ω with z=Az+Bz.

We begin with the following lemma.

Lemma 2.1For any φ,ψ∈PT(P,L),

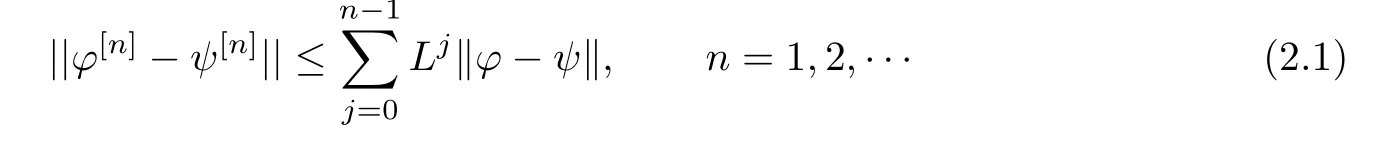
The result can be obtained by the definition of PT(P,L).

Lemma 2.2Suppose that a/=0 is given.If y∈PT(P,L),then y(t)is a solution of the equation(1.2)if and only if

Proof.Let y(t)∈PT(P,L)be a solution of(1.2).Multiplying both sides of(1.2)with eatand integrating the resulting equation from t to t+T,we obtain

Using the fact y(t+T)=y(t),the above expression can be put in the form

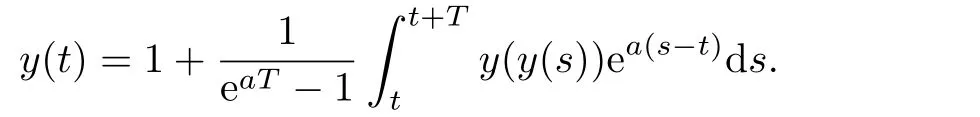
This completes the proof.

Now we construct two mappings to satisfy Theorem 2.1.Set the map A,B:PT(P,L)→PTas follows:

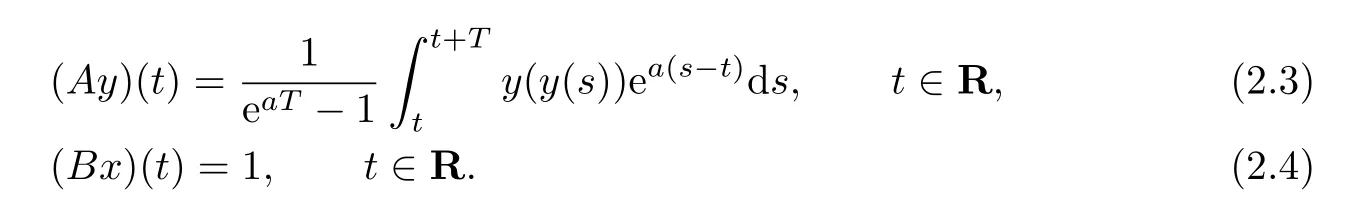
Lemma 2.3The operator A is continuous and compact on PT(P,L).

Proof.Take φ,ψ∈PT(P,L),t∈R.From(2.1)we obtain

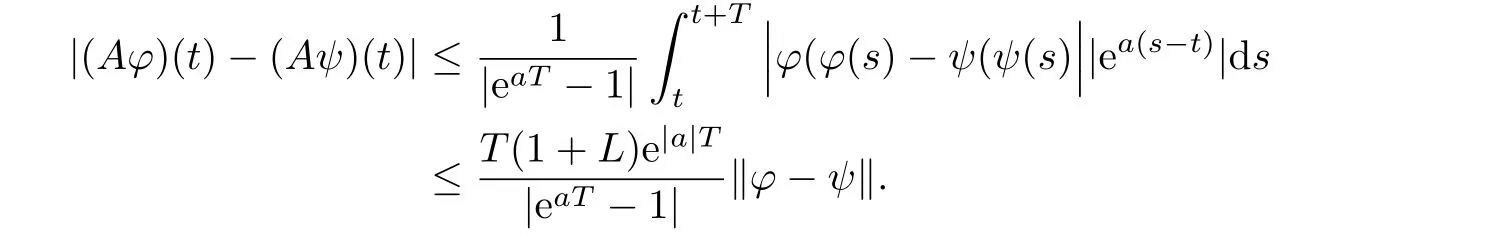
Thus A is continuous.

Now we show that A is a compact map.It is easy to see that PT(P,L)is uniformly bounded and equicontinuous on R,thus by Arzela-Ascoli theorem,it is a compact set.Since A is continuous,it maps compact sets into compact sets,therefore A is compact.This completes the proof.

Lemma 2.4The operator B is a contraction mapping on PT(P,L).

Proof.Take φ,ψ∈PT(P,L).Then

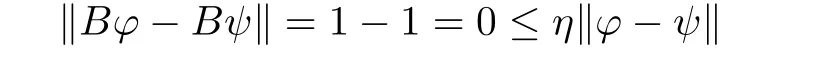
for any 0≤η＜1,hence B defines a contraction mapping.

Theorem 2.2Assume that the following inequalities hold:

Then(1.2)has a periodic solution in PT(P,L).

Proof.For any φ,ψ∈PT(P,L),from(2.5)we have

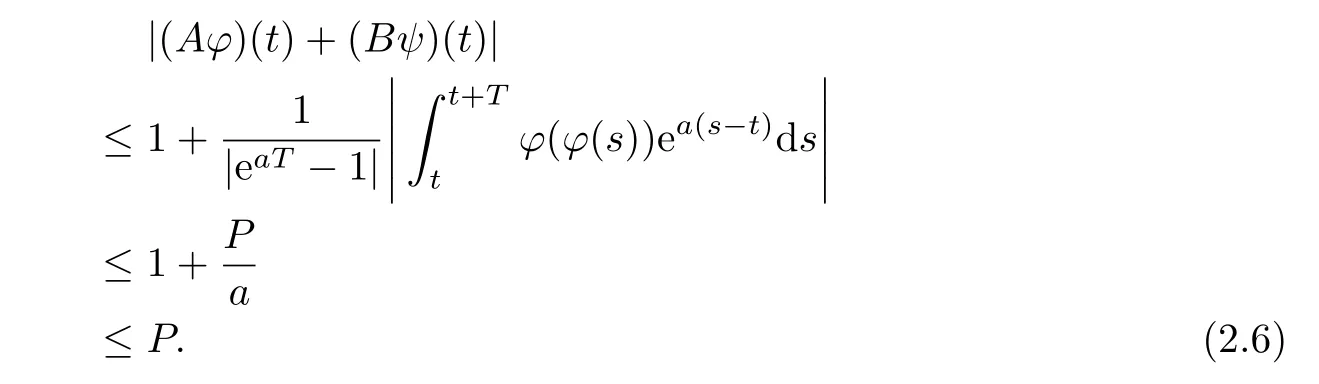
Without loss of generality,assume t2≥t1,from(2.5)we have

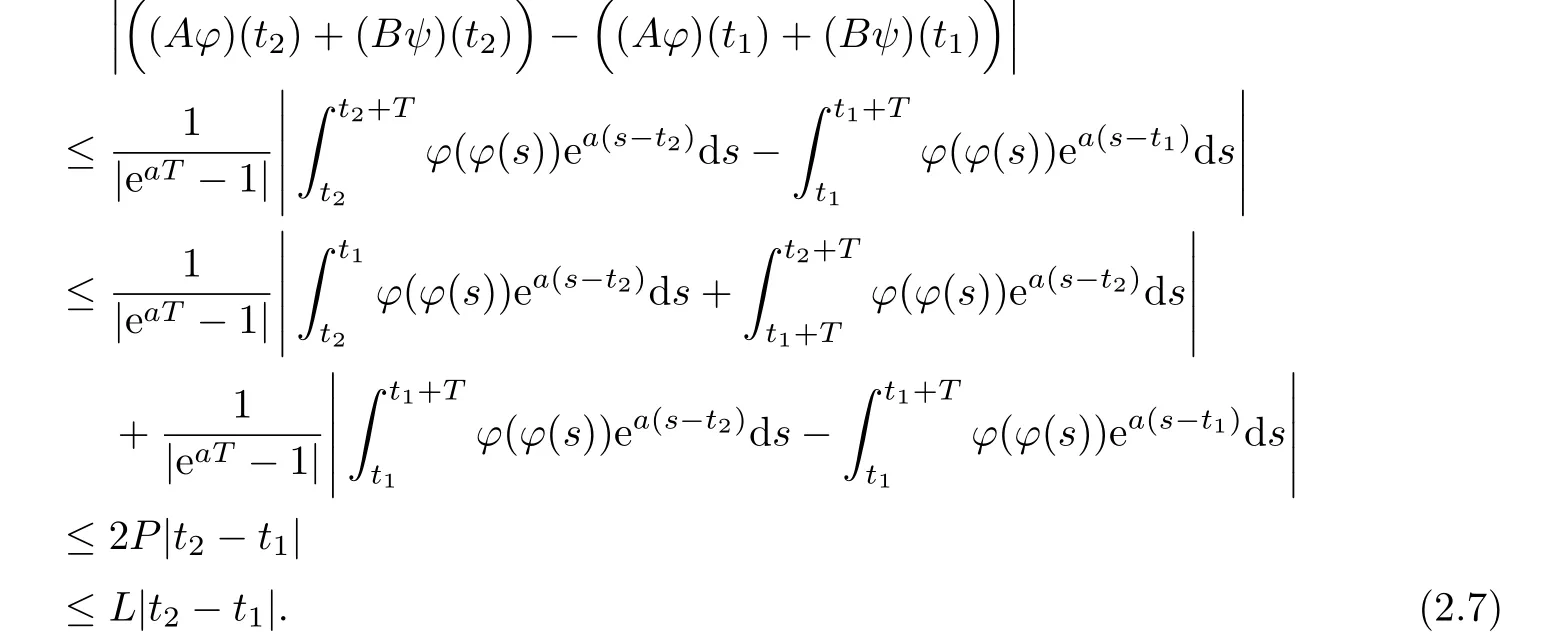
This shows that(Aφ)(t)+(Bψ)(t)∈PT(P,L).By Lemmas 2.3 and 2.4,we see that all the conditions of Krasnoselskii’s theorem are satisfied on the set PT(P,L).Thus there exists a fixed point y in PT(P,L)such that

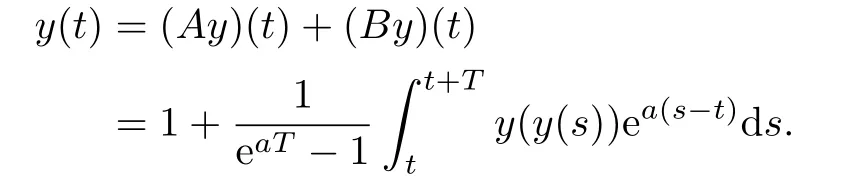
From Lemma 2.2 we can find(1.2)has a T-periodic solution.This completes the proof.

3 Solutions of(1.1)

In this section,the uniqueness and the stability of(1.2)are proved.Moreover,the existence of solution for(1.1)has been given.

Theorem 3.1In addition to the assumption of Theorem 2.2,suppose that

Then(1.2)has a unique solution in PT(P,L).

Proof.define an operator H from PT(P,L)into PT

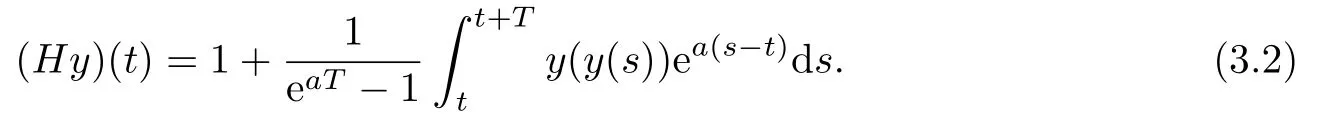
Denote φ,ψ∈PT(P,L)are two Different T-periodic solutions of(1.2).Then we have

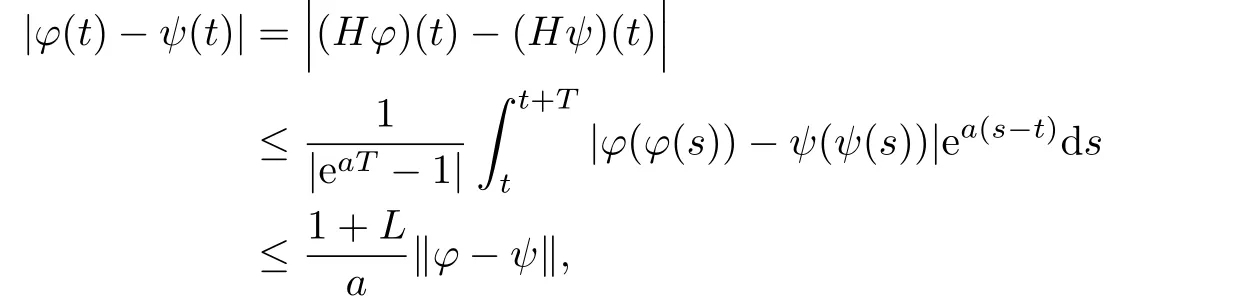
thus from(3.1)we get

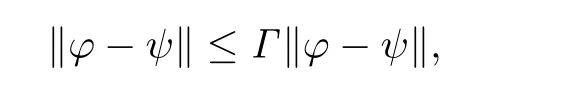
where

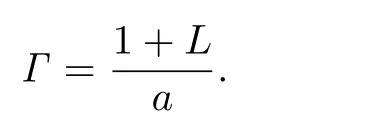
From(3.1)we know that Γ＜1 and the fixed point φ must be unique.

Theorem 3.2The unique solution obtained in Theorem 3.1 depends continuously on the given constant a.

Proof.Under the assumptions of Theorem 3.1,for any given constants a1≤a2satisfy(3.1),there are two unique corresponding functions φ(t)and ψ(t)in PT(P,L)such that

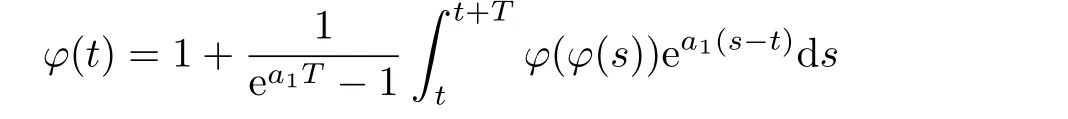
and

Then we have

thus

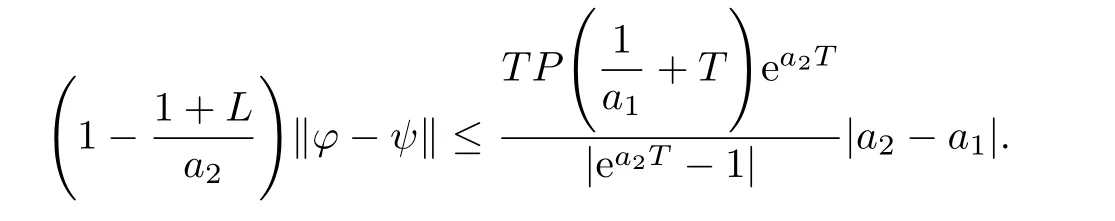
From(3.1)we have

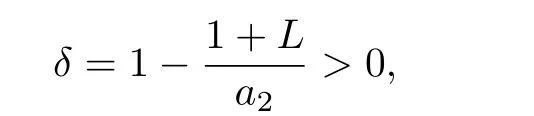
and then

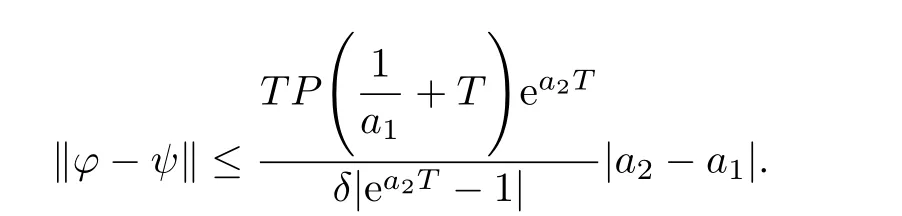
This completes the proof.

By Theorems 2.2,we may find a periodic solution y(t)of the auxiliary equation(1.2)such that y∈PT(P,L).Using the transform

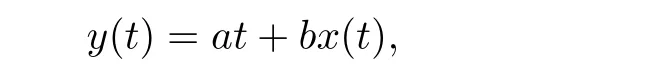
we can obtain the following theorem.

Theorem 3.3Suppose that b/=0.Under the conditions in Theorem 2.2,the solution of(1.1)can be expressed by a periodic function and a linear function.

Example 3.1We show that the conditions in Theorem 2.2 do not self-contradict.Consider the following equation:

Using

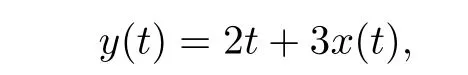
(3.4)can be changed into

Take P=2,L=6,after a simple calculation yields

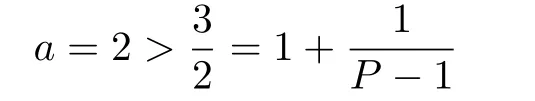
and

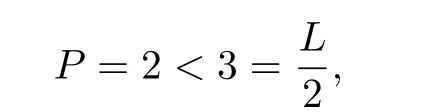
then(2.5)is satisfied.By Theorem 2.2,equation(3.5)has a T-periodic solution y such that‖y‖≤2,and

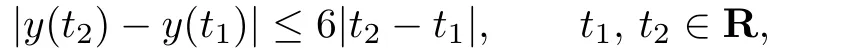
and

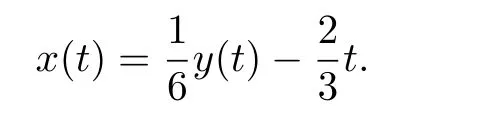
[1]McKiernan M A.The functional differential equationProc.Amer.Math.Soc.,1957,8:230–233.

[2]Si J G,Cheng S S.Analytic solutions of a functional differential equation with state dependent argument.Taiwan J.Math.,1997,1(4):471–480.

[3]Si J G,Zhang W N,Kim G H.Analytic solutions of an iterative functional differential equation.Appl.Math.Comput.,2004,150:647–659.

[4]Si J G,Ma M.Local invertible analytic solution of a functional differential equation with deviating arguments depending on the state derivative.J.Math.Anal.Appl.,2007,327:723–734.

[5]Burton T A.Stability by Fixed Point Theory for Functional differential Equations.New York:Dover,2006.

[6]Raffoul Y.Existence of periodic solutions in neutral nonlinear Difference systems with delay.J.Difference Equ.Appl.,2005,11(13):1109–1118.

[7]Guo Z,Yu J.Existence of periodic and subharmonic solutions for second-order superlinear Difference equations.Scientia Sinica Mathematica,2003,46(4):506–515.

[8]Chow S N.Existence of periodic solutions of autonomous functional differential equations.J.differential Equations,1974,15:350–378.

[9]Kaufmann E R,Raffoul Y.Periodic solutions for a neutral nonlinear dynamical equation on a time scale.J.Math.Anal.Appl.,2006,319:315–325.

[10]Raffoul Y.Positive periodic solutions of nonlinear functional Difference equations.Electron.J.differential Equations,2002,55:1–8.

[11]Raffoul Y.Positive periodic solutions in neutral nonlinear differential equations.Electron.J.differential Equations,2007,16:1–10.

[12]Zhou Z,Yu J,Guo Z.Periodic solutions of higher-dimensional discrete systems.Proc.Roy.Soc.Edinburgh Sect.A,2004,134:1013–1022.

[13]Smart D R.Fixed Points Theorems.Cambridge:Cambridge University Press,1980.

39B12,39B82

A

1674-5647(2017)04-0311-07

10.13447/j.1674-5647.2017.04.03

date:June 7,2016.

The NSF(11326120 and 11501069)of China,the Foundation(KJ1400528 and KJ1600320)of Chongqing Municipal Education Commission and the Foundation(02030307-00039)of Youth Talent of Chongqing Normal University.

E-mail address:houyu19@gmail.com(Zhao H Y).