Shared Values of Certain Nonlinear differential Polynomials of Meromorphic Functions

CHEN JUN-FAN AND CAI XIAO-HUA

(Department of Mathematics,Fujian Normal University,Fuzhou,350117)

Shared Values of Certain Nonlinear differential Polynomials of Meromorphic Functions

CHEN JUN-FAN AND CAI XIAO-HUA

(Department of Mathematics,Fujian Normal University,Fuzhou,350117)

Communicated by Ji You-qing

In this paper,by using the idea of truncated counting functions of meromorphic functions,we deal with the problem of uniqueness of the meromorphic functions whose certain nonlinear differential polynomials share one finite nonzero value.

meromorphic function,shared value,differential polynomial,uniqueness

1 Introduction and Main Results

In this paper,by meromorphic function we always means a function which is meromorphic in the whole complex plane C.We adopt the usual and standard notations in the Nevanlinna theory of meromorphic functions such as T(r,f),N(r,f),,m(r,f)and so on(see[1]–[3]).For a meromorphic function f,we denote by S(r,f)any quantity satisfying S(r,f)=o{T(r,f)},as r→+∞,possibly outside a set of finite measure.

Let f be a nonconstant meromorphic function,a be a complex number,and m be a positive integer.We denote by E(a,f)the set of zeros of f−a,where a zero with multiplicity m is counted m times in the set.If these zeros are only counted once,then we denote the set by.In addition,we denote by Em)(a,f)the set of zeros of f−a with multiplicity l≤m,where a zero with multiplicity l≤m is counted l times in the set.Similarly,if these zeros are only counted once,then we denote the set by

Let f and g be two nonconstant meromorphic functions,and a be a complex number.If f−a and g−a have the same zeros with the same multiplicities,i.e.,E(a,f)=E(a,g),then we say that f and g share a CM(counting multiplicities).And if we do not consider the multiplicities,i.e.,then we say that f and g share a IM(ignoring multiplicities).

For any constant a∈C∪{∞},we define

Also we use the notations δ(a)and Θ(a),where δ(a)=min{δ(a,f),δ(a,g)}and Θ(a)=min{Θ(a,f),Θ(a,g)}.

Meanwhile,the order λ and the lower orderµof a meromorphic function f are defined in turn as follows:

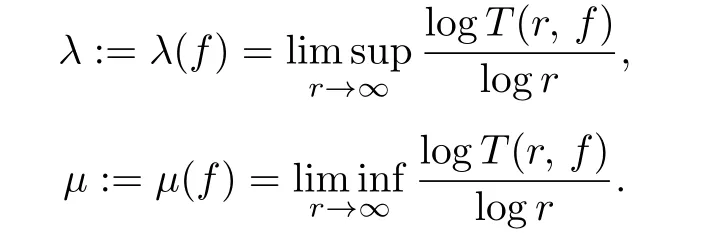
Nevanlinna[4]pointed out that if f and g share four distinct values CM,then f is a M¨obius transformation of g.In recent decades,related to one famous conjecture of Hayman[5],many interesting uniqueness theorems for certain types of differential polynomials with one shared value were obtained.

In 2002,Fang[6]proved the following uniqueness theorem.

Theorem 1.1Let f and g be two nonconstant entire functions,and n,k be two positive integers with n≥2k+8.If(fn(f−1))(k)and(gn(g−1))(k)share 1 CM,then f≡g.

In 2008,Chen et al.[7]generalized Theorem 1.1 by deriving the following result.

Theorem 1.2Let f and g be two nonconstant entire functions,and let n,k be two positive integers with n＞5k+13.If(fn(f−1))(k)and(gn(g−1))(k)share 1 IM,then f≡g.

In 2011,Lin X.Q.and Lin W.C.[8]proved the following result which was an improvement of Theorem 1.2.

Theorem 1.3Let f and g be two nonconstant entire functions,and n,k and m≥2 be three positive integers with n＞k+(4k+7)(1−Θ(0))+4(1−δ(1)).Ifthen f≡g.

The above results have undergone various extensions from Different directions.In 2014,by using Zalcman’s lemma,Li and Yi[9]considered the case of meromorphic functions and proved the following result which was a generalization of Theorem 1.2.

It is natural to ask whether Theorem 1.4 can be extended in the same way that Theorem 1.3 extends Theorem 1.2.

The purpose of the paper is to study this problem.In this paper,by using the idea of truncated counting functions of meromorphic functions,we o ff er such an extension by establishing the following theorem.

Theorem 1.5Let f and g be two nonconstant meromorphic functions such that λ(f)＞2,and n,k and m≥2 be three positive integers with n＞max{γ,2k+2},where γ=(4k+7)(1−Θ(∞))+(5k+7)(1−Θ(0))+5(1−δ(1))−1.Ifandthen f≡g.

Corollary 1.2Let f and g be two nonconstant meromorphic functions such that λ(f)＞2,and n,k and m≥2 be three positive integers with n＞9k+18.Ifandthen f≡g.

Corollary 1.3Suppose that the condition n＞9k+20 is replaced by n＞9k+18 in Theorem 1.4.Then the conclusion remains valid.

Example 1.1[9]Let n,k be two positive integers,and

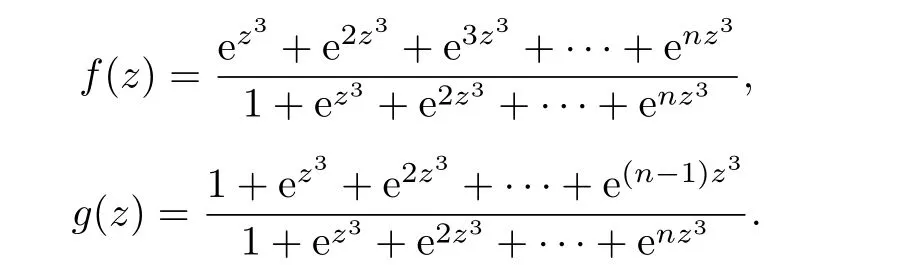
Then fn(f−1)=gn(g−1),Θ(∞,f)=0,λ(f)=3,(fn(f−1))(k)and(gn(g−1))(k)share 1 CM.However,f/≡g.

2 Some Lemmas

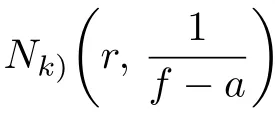
Obviously,

Let f and g be two nonconstant meromorphic functions such thatwhere m≥2 is a positive integer.Let z0be a zero of f−1 of multiplicity p,a zero of g−1 of multiplicity q.We denote bythe reduced counting function of those zeros of f−1 where p＞q,bythe counting function of those zeros of f−1 where p=q=1,bythe reduced counting function of those zeros of f−1 where p=q≥2.Also we denote bythe counting function of those zeros of f′that are not zeros of f and f−1,bythe corresponding reduced counting function.Similarly,we introduce the notations

Lemma 2.2[11],[12]Let f be a nonconstant meromorphic function,and p,k be two positive integers.Then

Lemma 2.3Let f and g be two nonconstant meromorphic functions,m≥2 be a positive integer,and

and the same inequality holds for T(r,g).

Noting that

we have

From this,and by(2.2)and(2.3),we have

By the second fundamental theorem,we obtain

Combining(2.4)with(2.5)yields

Lemma 2.4Let f and g be two nonconstant meromorphic functions,and n,k and m be three positive integers with n≥k.If,then

Proof.From the assumption and Lemma 2.2(p=1),we get

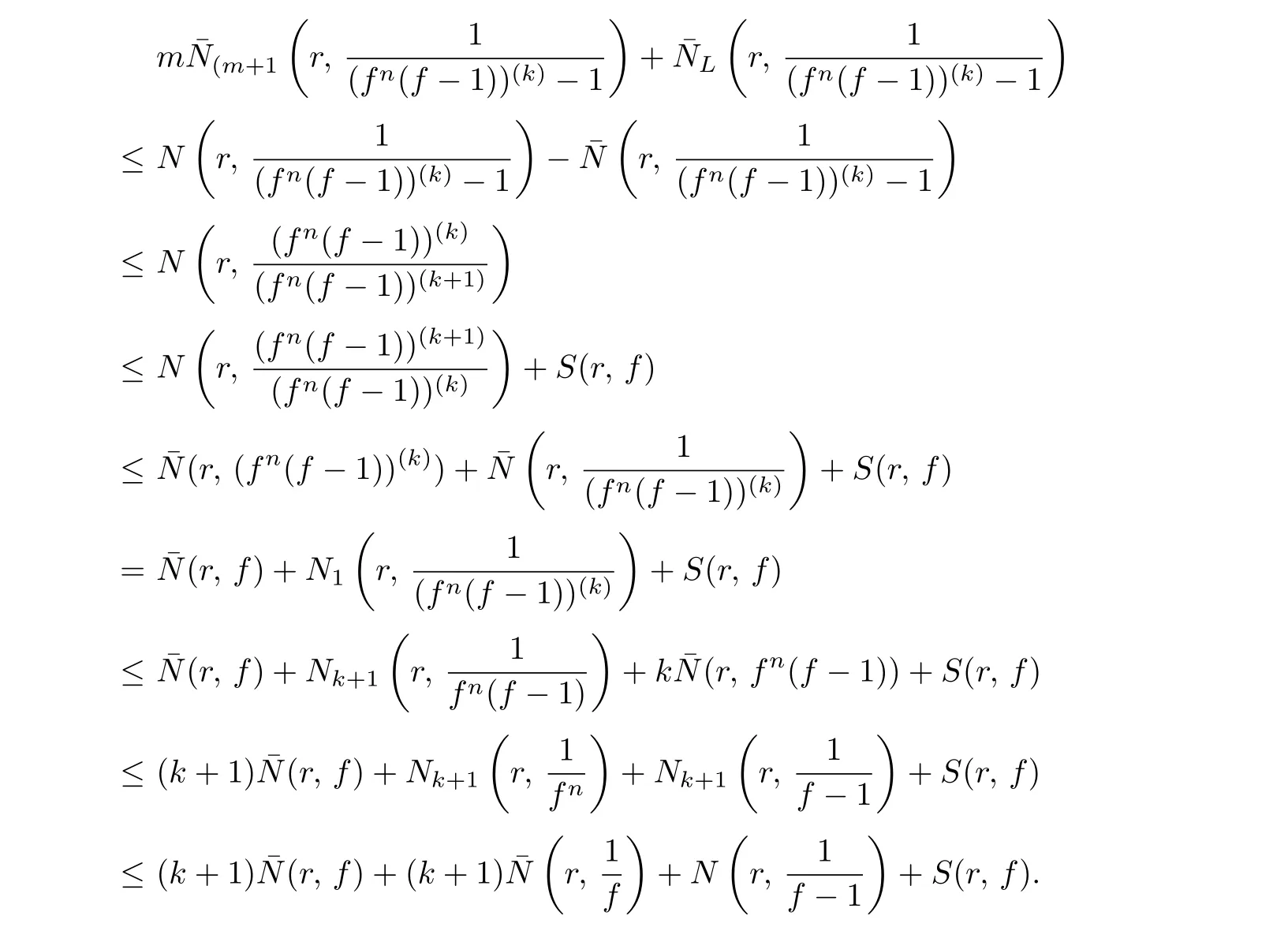
Lemma 2.5[3]Let f be a nonconstant meromorphic function,and k be a positive integer.Then

Lemma 2.6[13]Let f and g be two nonconstant meromorphic functions,and h be given by(2.1)in Lemma 2.3.If h≡0 and

where T(r)=max{T(r,f),T(r,g)},and I is a set of in finite linear measure of 0＜r＜∞,then fg≡1 or f≡g.

Lemma 2.7[9]Let f and g be two nonconstant meromorphic functions,and n,k be two positive integers with n＞2k.If≡1,then λ(f)≤2 and λ(g)≤2.

Lemma 2.8Let f and g be two nonconstant meromorphic functions such that λ(f)＞2,and n,k be two positive integers with n＞max{γ1,2k},where γ1=2(k+1)(1−Θ(∞))+(3k+2)(1−Θ(0))+3(1−δ(1))−1.Set

and

If H≡0,then F≡G.

Proof.Note that

From this,and by(2.6),Lemmas 2.1 and 2.5,we get

Similarly,

Now it follows by(2.8)and(2.9)for arbitrary ε＞0 that

On the other hand,from Lemma 2.2(p=1),for the above ε＞0,we have

Considering the assumptions that H≡0 and n＞max{γ1,2k},where γ1=2(k+1)(1−Θ(∞))+(3k+2)(1−Θ(0))+3(1−δ(1))−1,by(2.7),(2.10),(2.11)and Lemma 2.6,we obtain FG≡1 or F≡G.Thus,by the assumption λ(f)＞2 and Lemma 2.7,we get F≡G.

3 Proof of Theorem 1.5

Let F,G and H be given by(2.6)and(2.7)in Lemma 2.8.Then by the assumption we have

Next we discuss the following two cases.

Case 1.Suppose that H/≡0.Then it follows from Lemma 2.3 that

By Lemma 2.2(p=2)we get

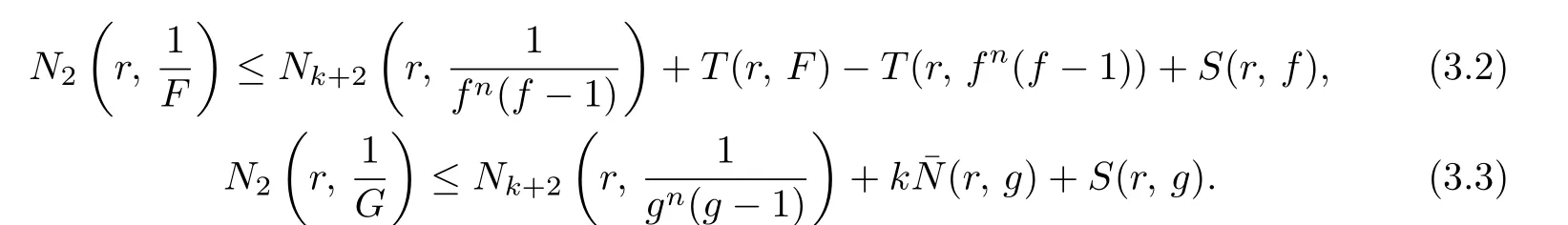
From Lemma 2.4 we obtain

Now it follows from(3.1)–(3.4)and Lemma 2.1 that

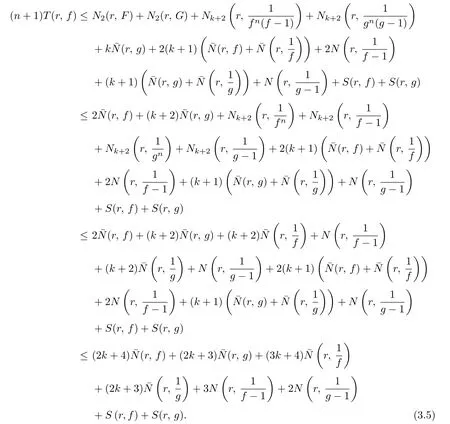
Similarly,

Thus,from(3.6)and(3.7)for arbitrary ε＞0,we have

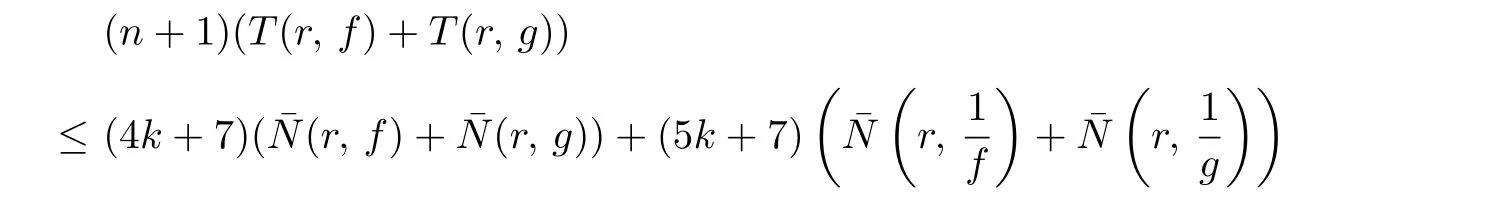
which contradicts the assumption n＞max{γ,2k+2},where γ=(4k+7)(1−Θ(∞))+(5k+7)(1−Θ(0))+5(1−δ(1))−1.Hence this case does not hold.

Case 2.Suppose that H≡0.Then by the assumption and Lemma 2.8 we obtain F≡G,i.e.,

It follows that

where p is a polynomial of degree at most k−1.

We claim that p≡0.

If p/≡0,then by(3.7)we get

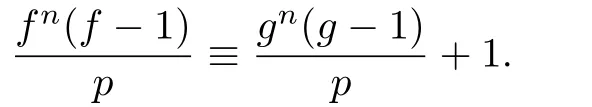
Since f is nonconstant meromorphic,logr≤T(r,f).By the second fundamental theorem,Lemma 2.1 and degp≤k−1,we have

and so

This implies that

Similarly,

Combining(3.8)with(3.9)yields

It follows that n≤2k+2,contradicting n＞2k+2.Hence the claim is proved and by(3.7)we obtain

Thus,from(3.11)and Lemma 2.1,we deduce

It follows from(3.11),(3.12)and the second fundamental theorem that

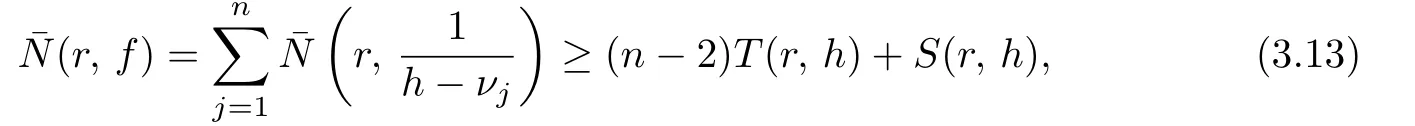
where ν1,ν2,···,νnare finite values with νj/=1 andfor 1≤j≤n.From(3.12)and(3.13)we get

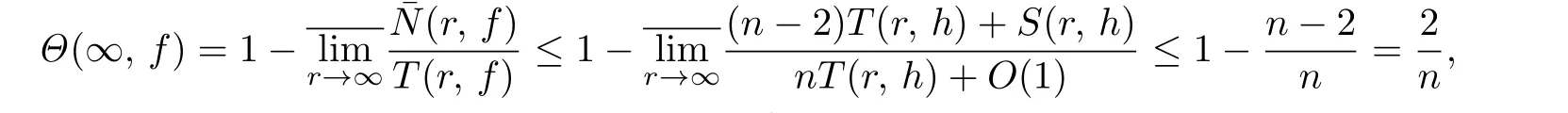
which contradicts the assumptionTherefore,we deduce that h≡1,that is,f≡g.

[1]Hayman W K.Meromorphic Functions.Oxford:Clarendon Press,1964.

[2]Yang L.Value Distribution Theory.Berlin:Springer-Verlag,1993.

[3]Yi H X,Yang C C.Uniqueness Theory of Meromorphic Functions(in Chinese).Beijing:Science Press,1995.

[4]Nevanlinna R.Les Th´eor´eme de Picard-Borel et la Th´eorie des Fonctions M´eromorphes.Paris:Gauthier-Villars,1929.

[5]Hayman W K.Research Problems in Functions Theory.London:Athlone Press,1967.

[6]Fang M L.Uniqueness and value-sharing of entire functions.Comput.Math.Appl.,2002,44:823–831.

[7]Chen J F,Zhang X Y,Lin W C,Chen S J.Uniqueness of entire functions that share one value.Comput.Math.Appl.,2008,56:3000–3014.

[8]Lin X Q,Lin W C.Uniqueness of entire functions sharing one value.Acta Math.Sci.,2011,31B(3):1062–1076.

[9]Li X M,Yi H X.Remarks on value sharing of certain differential polynomials of meromorphic functions.Bull.Austral.Math.Soc.,2014,90(3):427–443.

[10]Mokhonko A Z.On the Nevanlinna characteristics of some meromorphic functions.Funct.Anal.Appl.,1971,14:83–87.

[11]Lahiri I,Sarkar A.Uniqueness of a meromorphic function and its derivative.J.Inequal.Pure Appl.Math.,2004,5(1):Article 20.

[12]Zhang J L,Yang L Z.Some results related to a conjecture of R.Br¨uck.J.Inequal.Pure Appl.Math.,2007,8(1):Article 18.

[13]Yi H X.Meromorphic functions that share one or two values.Complex Var.Theory Appl.,1995,28(1):1–11.

30D30,30D35

A

1674-5647(2017)04-0347-12

10.13447/j.1674-5647.2017.04.07

date:July 27,2016.

The NSF(11301076)of China and the NSF(2014J01004)of Fujian Province.

E-mail address:junfanchen@163.com(Chen J F).