Topological Tail Pressure for Asymptotically Sub-additive Continuous Potentials

DING DAN-DAN,MA XIAN-FENG,*AND CHEN ER-cAI

(1.Department of Mathematics,East China University of Science and Technology,Shanghai,200237)

(2.School of Mathematical Science,Nanjing Normal University,Nanjing,210097)

(3.Center of Nonlinear Science,Nanjing University,Nanjing,210093)

Topological Tail Pressure for Asymptotically Sub-additive Continuous Potentials

DING DAN-DAN1,MA XIAN-FENG1,*AND CHEN ER-cAI2,3

(1.Department of Mathematics,East China University of Science and Technology,Shanghai,200237)

(2.School of Mathematical Science,Nanjing Normal University,Nanjing,210097)

(3.Center of Nonlinear Science,Nanjing University,Nanjing,210093)

Communicated by Lei Feng-chun

We define the topological tail pressure and the conditional pressure for asymptotically sub-additive continuous potentials on topological dynamical systems and obtain a variational principle for the topological tail pressure without any additional assumptions.

asymptotically sub-additive potential,tail pressure,entropy structure,variational principle

1 Introduction

In this paper,we call(X,T)a topological dynamical system(TDS for short)if(X,d)is a compact metric space,T:X→X is a surjective and continuous map with finite topological entropy.

Topological pressure is a generalization of topological entropy,the theory of topological pressure,variational principles,equilibrium states and related topics plays a fundamental role in statistical mechanics,ergodic theory,and dynamical systems(see[1]–[5]).

Ruelle[6]first introduced the notion of the topological pressure and presented the related variational principle for additive potentials of expansive maps on compact metric spaces.Later,Walters[7]generalized the result to the general continuous maps on compact metricspaces:

Let(X,T)be a TDS,f:X→R be an arbitrary continuous function and P(T,f)be the topological pressure of f.Then

where M(X,T)denotes the space of all T-invariant measures on X and hµ(T)denotes the measure-theoretical entropy ofµ.

In[8],Cao et al.defined the topological pressure and set up a variational principle for sub-additive potentials on general compact metric spaces without any additional assumptions.Then Feng et al.[9]extended the result to the case of asymptotically sub-additive potentials:

where

Li et al.[10]defined the tail pressure and established a variational principle for continuous transformations on compact metric spaces:

Let(X,T)be a TDS,f:X→R be continuous,and P(T,f)be the tail pressure of f.Then

where

and H=(hk)k∈Nis an entropy structure defined on M(X,T).Moreover,the supremum can be achieved on the closure of the ergodic measures.When f=0,the definition is equivalent with the tail entropy defined in[11].Ding et al.[12]generalized the result to the sub-additive potentials:

Let(X,T)be a TDS,F={fn}n∈Nbe a sub-additive potential,and P∗(T,F)be the topological pressure of F.Then

Moreover,the supremum can be achieved on the closure of the ergodic measures.When F={f},the result is equivalent to that in[10].

The purpose of this paper is to extend above results to the case of asymptotically subadditive potentials.We give a definition of the tail pressure for asymptotically sub-additive potentials,and establish a variational principle which implies the relation between the tail pressure and the tail entropy function.

We first introduce the definition of asymptotically sub-additive potentials before formulating our results,we take it from[9].

Let(X,T)be a TDS,C(X,R)be the space of all continuous real-valued functions on X.A sequence F={fn}n∈Nof functions in C(X,R)is said to be a sub-additive potential if for any m,n∈N and x∈X,

F={fn}n∈Nis said to be an asymptotically sub-additive potential if for any ϵ＞0,there exists a sub-additive potentialon X such that

Letµ∈M(X,T).define

Then F∗(µ)exists and is upper semi-continuous(see[9]).

Let SXbe the space of all asymptotically sub-additive real continuous potentials,M(X)be the set of all Borel probability measures on X,M(X,T)be the set of T-invariant measures,and Me(X,T)be the set of T-invariant ergodic measures.It is clear that

and M(X),M(X,T)are convex,compact metric spaces endowed with the weak*-topology.

Our main results are the following theorems.

Theorem 1.1If(X,T)is a TDS,F∈SXand P=(Pk)k∈Nis a re fining sequence of essential partitions,then

In particular,

Theorem 1.2If(X,T)is a TDS with finite topological entropy and F∈SX,then

Moreover,the supremum can be achieved on the closure of the ergodic measures.

This paper is organized as follows:In Section 2,we introduce the topological tail pressure and the conditional pressure with respect to partitions for asymptotically sub-additive potentials,and recall some basic properties of the entropy structures.In Section 3,we state and prove the variational principle of the topological tail pressure.

2 Topological Tail Pressure and the Entropy Structure

In this section,we give the definition of the topological tail pressure using separated subsets and conditional pressure with respect to partitions for asymptotically sub-additive potentials and related properties,the entropy structure and related properties,and the main Theorem 1.1.

We first recall some basic notations.Let(X,T)be a TDS.We use the notation B(x,n,ϵ)for the Bowen’s ball of order n with radius x and center at x:

A set E⊂X is said to be an(n,δ)-spanning subset of K if

and an(n,δ)-separated subset of K if for all x,y∈E with x/=y implies

If E is an(n,δ)-separated subset of K with the maximal cardinality,then it is also an(n,δ)-spanning subset of K.

Now,we introduce the topological tail pressure for asymptotically sub-additive potentials.Let F∈SX,n∈N,ϵ＞0 and δ＞0.For all x∈X we define

It is clear that Pn(T,F,x,δ,ϵ)is decrease in δ,and increase in ϵ.

Let F∈SX,ϵ＞0 and δ＞0,define

P(T,F,δ,ϵ)is also decrease in δ,and increase in ϵ.

Let(X,T)be a TDS,F∈SX.The topological tail pressure of F is defined as

Then F(k)is a subsequence of F,and F(k)∈SX.The following proposition is the power rule for the asymptotically sub-additive potentials.

Proof.Fix k∈N.If E is an(n,δ)-separated subset of B(x,n,ϵ)with respect to Tk,then E is also an(nk,δ)-separated subset of B(x,n,ϵ)with respect to T.Thus,

Then we obtain

For the opposite inequality,since T is continuous,for any η＞0,there exists δ＞0,such that d(x,y)＜δ implies

And if E is an(nk,η)-separated subset of B(x,n,ϵ)with respect to T,then E is also an(n,δ)-separated subset of B(x,n,ϵ)with respect to Tk.Thus,

Then we get

The proof is completed.

Now we recall the notations of the extension and the entropy structure adopted by Burguet[13].Let(Y,S)and(X,T)be two TDSs and π:Y→X be a continuous map not necessarily surjective,but such that the induced map π∗:M(Y,S)→M(X,T)is surjective.We refer to π and also to(Y,S)as an extension of(X,T)if S◦π=π◦T.An extension is called zero dimensional if the topological dimension of Y is zero or,equivalently,if Y has a base consisting of clopen sets.An extension π:(Y,S)→(X,T)is said to be principal if for any ν∈M(Y,S),h(π∗ν)=h(ν).

The natural extension of(X,T)is defined as follows.Denote

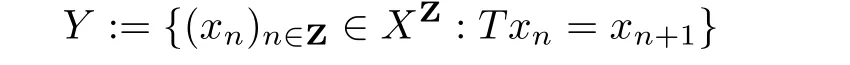
and the projection π:Y→X defined by

We endow Y with the metric

The natural extension is an extension as defined above and this extension is principal.

A non-decreasing sequence of real functions H=(hk)k∈Ndefined on M(X,T),converging to a bounded limit,is called a candidate of M(X,T).

Two candidates of(X,T)are said to be uniformly equivalent if for all γ＞0 and for all k∈N,there exists an l∈N such that

Let π:(Y,S)→(X,T)be an extension and H=(hk)k∈Nbe a candidate of(X,T).The lift π∗H of H to(Y,S)is the candidate of(Y,S)defined by

Let(Y,S)be a zero-dimensional principal extension of(X,T)with finite topological entropy and(Pk)k∈Nbe a re fining sequence of clopen partitions of Y.An entropy structure H=(hk)k∈Nis a candidate of(X,T)such that the lift π∗H of H to M(Y,S)is uniformly equivalent to the candidate(h(·,Pk))k∈N.

Two entropy structures are uniformly equivalent and any candidate,which is uniformly equivalent to an entropy structure,is also an entropy structure.In other words,the set of entropy structures is an equivalence class for the uniform equivalence relation on the set of candidates.Moreover,the lift of an entropy structure is also an entropy structure for the principal extension(see[14]–[15]for more details).

Let H=(hk)k∈Nbe a candidate.For a function f:M(X,T)→R+,denote the smallest upper semi-continuous function greater than f bythat is,

define

All entropy structures H converge to the metric-theoretic entropy and have the same uH.So we denote it by u for convenience.

Lemma 2.1[12]If(Y,)is the natural extension of(X,T)and ϵ＞0,then there exists an N∈N such that for each x∈X,n∈N,

where A is a finite subset of Y with♯A≤N.

Proposition 2.2If(Y,)is the natural extension of(X,T)and F∈SX,then

Remark 2.1The proposition has been proved for the case of sub-additive potentials in[12],we can see that it is also works well for the asymptotically sub-additive potentials.

Lemma 2.2[11]Let(fk)kbe a non-increasing sequence of upper semi-continuous functions on a compact domain K.Then

Lemma 2.3If H=(hk)k∈Nis a candidate of a TDS(X,T),and F∈SX,then we have the following properties:

(1)The function uH+F∗is upper semi-continuous in M(X,T).In particular,uH+F∗attains its supremum;

Remark 2.2These properties have been proven in[12],and they also work well for our definition.

Then we introduce the conditional pressure for asymptotically sub-additive potentials.Recall that a cover of X is a finite family of Borel subsets of X whose union is X,and a partition of X is a cover of X whose elements are pairwise disjoint.For given two covers U and V,U is said to be finer than V if each element of U is contained in some element of V.A partition is said to be essential if the boundaries of its elements have zeroµ-measure for allµ∈M(X,T).A sequence of partitions P=(Pk)k∈Nis said to be re fining if Pk+1is finer than Pkfor all k∈N and if the diameter of Pkgoes to zero,when k goes to in finity.

Lemma 2.4[16]If T is a homeomorphism of finite topological entropy admitting an in finite minimal factor,then there exists a re fining sequence of essential partitions.

Let P and Q be two partitions with Q finer than P.For n∈N,A∈Pnand F∈SX,define

It is clear that Mn(T,F,A,Q|P)is increase in Q and decrease in P.The conditional pressure of F with respect to P and Q is defined as

If P=(Pk)k∈Nis a re fining sequence of partitions,then the conditional pressure of F with respect to P is defined as

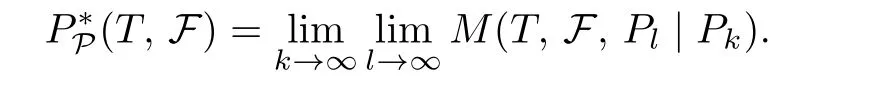
Lemma 2.5If(X,T)is a TDS,F∈SXand P=(Pk)k∈Nis a re fining sequence of partitions,then

and equals to

define

According to the definition of F,for any ϵ＞0,there exists a sub-additive potential G={gn}n∈Non X such that

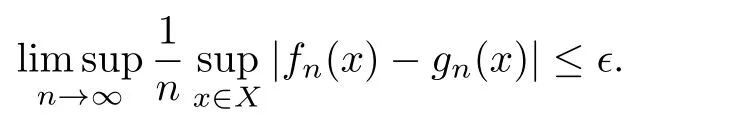
Let

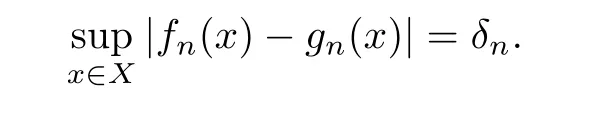
So

and

then we can get

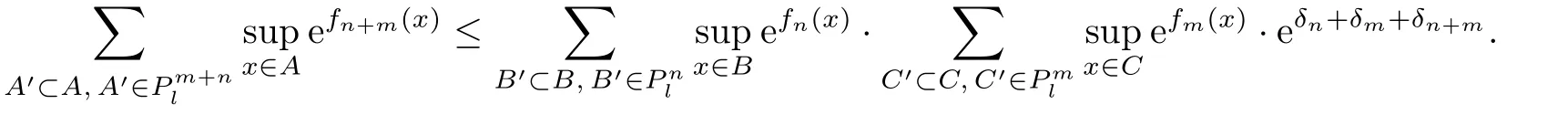
Then

and

Lemma 2.6[13]If(X,T)is a TDS and P is an essential partition,then for each ϵ＞0,there exists δ＞0 such that

Theorem 1.1If(X,T)is a TDS,F∈SXand P=(Pk)k∈Nis a re fining sequence of essential partitions,then

In particular,

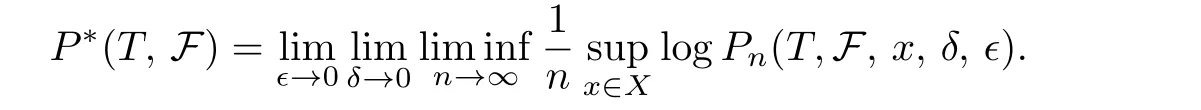
The following proposition is the product rule for the asymptotically sub-additive potentials.

Proposition 2.3Let(Xi,Ti),i=1,2 be two TDSs andi=1,2.For each x1∈X1,x2∈X2,n∈N and F1×F2∈C(X1×X2,R),define

then

Remark 2.3Theorem 1.1 and Proposition 2.3 have been proved in[12]and they also hold for our case of asymptotically sub-additive potentials.

3 Variational Principle for Asymptotically Sub-additive Potentials

In this section,the variational principle of topological tail pressure for asymptotically subadditive potentials is stated as Theorem 1.2.

Theorem 1.2If(X,T)is a TDS with finite topological entropy and F∈SX,then

Moreover,the supremum can be achieved on the closure of the ergodic measures.

To prove Theorem 1.2,we first recall some useful lemmas.

and the equality holds if and only if

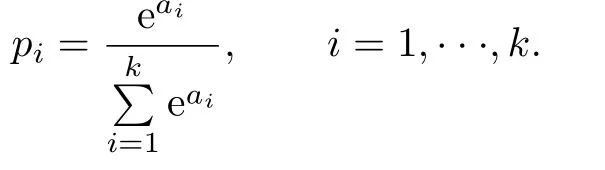
Lemma 3.2[9]Suppose thatis a sequence in M(X).We form the new sequenceby

Assume thatµniconverges toµin M(X)for some subsequence{ni}of natural numbers.Thenµ∈M(X,T)and

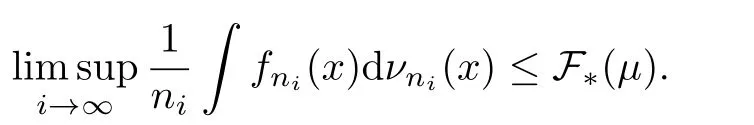
Lemma 3.3[17]If λ∈[0,1]andµ,ν are two probability measures of X.Then for any two partitions P and Q of X,

Lemma 3.4[17]If A,B,C,D are partitions of X andµ∈M(X),then

Now,we prove Theorem 1.2.

Proof of Theorem 1.2First we prove the variational principle when(X,T)admits a re fining sequence of essential partitions,

Fix l＞k∈N and denote α(C)=sup{fn(x)|x∈C)}for each.Recall that for any Borel probability measureµ,

Thus we have

Therefore,

(2)Next,we prove the opposite inequality,i.e.,

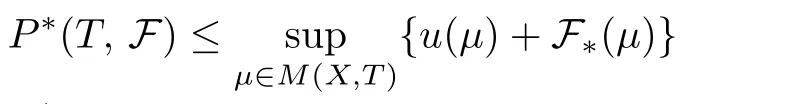
by find measure η∈M(X,T)satisfying

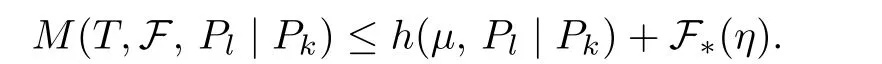
Let

define the probability measuresµnand νnas follows:

Since M(X)is compact,we can choose a subsequence{nj}of N such that

and{νnj}converges in M(X)to some η∈M(X,T).Sinceµnis supported by

Moreover,since each element ofcontains at most one point in E,then either

or

Summing this over j from 0 to m−1,we have

Dividing by n yields

Since xB∈E and

for each B∈An,

Since Pland Pkare essential partitions,we have

Replacing n by njin the inequality(3.1)and using Lemma 3.2,we have

Dividing by m and letting m converges to in finity,we get

Letting l→∞and then k→∞,by Lemma 2.4 we have

Since the functions h(·,Pl|Pk)and F∗(·)are both affine and upper semi-continuous,the supremum can be achieved at some ergodic measure.

In general case,by Lemma 2.4,the product of the natural extension of(X,T)with the irrational rotation Rθon the circleadmits a re fining sequence of essential partitions,where θ is an irrational number.It follows from the above argument that

where

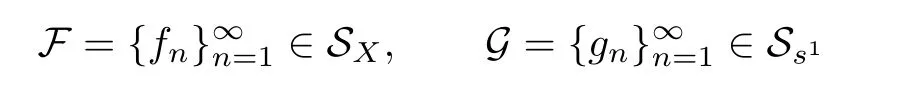
and F◦π×G is defined as

If G≡0,by Proposition 2.2 we have

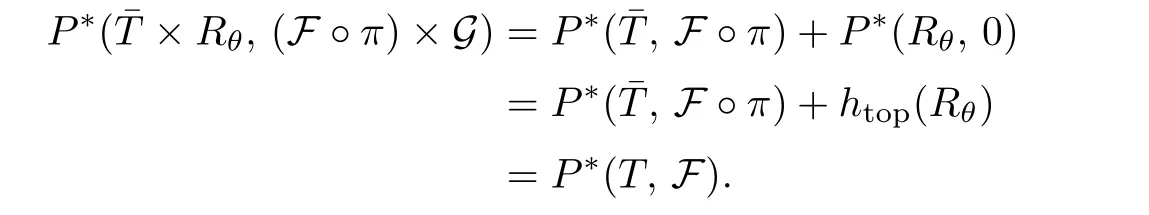
By Lemma 2.3,we have

Therefore,

The proof is completed.

[1]Huang X,Wen X,Zeng F.Topological pressure of non-automomous dynamical systems.Nonlinear Dyn.Syst.Theory.,2008,8(1):43–48.

[2]Huang W,Yi Y.A local variational principle of pressure and its applications to equilibrium states.Israel J.Math.,2007,161(1):29–74.

[3]Pesin Ya.Dimension type characteristics for invariant sets of dynamical systems.Russian Math.Surveys.,1988,43(4):111–151.

[4]Pesin Ya,Pitskel B.Topological pressure and the variational principle for non-compact sets.Funct.Anal.Appl.,1984,18(4):307–318.

[5]Pollner P,Vattay G.New method for computing topological pressure.Phys.Rev.Lett.,1996,76(22):4155–4163.

[6]Ruelle D.Statistical mechanics on a compact set with Zνaction satisfying expansiveness and specification.Trans.Amer.Math.Soc.,1973,187:237–251.

[7]Walters P.A variational principle for the pressure of continuous transformations.Amer.J.Math.,1975,97:937–971.

[8]Cao Y,Feng D,Huang W.The thermodynamic formalism for sub-additive potentials.Discrete Contin.Dyn.Syst.,2008,20:259–273.

[9]Feng D,Huang W.Lyapunov spectrum of asymptotically sub-additive potentials.Commun.Math.Phys.,2010,297:1–43.

[10]Li Y,Chen E,Cheng W.Tail pressure and the tail entropy function.Ergodic Theory Dynam.Systems,2012,32:1400–1417.

[11]Boyle M,Downarowicz T.The entropy theory of symbolic extension.Invent.Math.,2004,156:119–161.

[12]Ding D,Zhang Z,Ma X,Chen E.Variational principle for topological tail pressures with sub-additive upper semi-continuous potentials.Dyn.Syst.,2016,31:198–220.

[13]Burguet D.A direct proof of the tail variational principle and its extension to maps.Ergodic Theory Dynam.Systems,2009,29:357–369.

[14]Downarowicz T.Entropy structure.J.Anal.Math.,2005,96:57–116.

[15]Downarowicz T.Entropy in Dynamical Systems.Cambridge:Cambridge University Press,New Mathematical Monographs 18,2011.

[16]Lindenstrauss E.Mean dimension,small entropy factors and an embedding theorem.Math.Inst.Hautes´Etudes Sci.,1999,89:227–262.

[17]Walters P.An Introduction to Ergodic Theory.New York:Springer-Verlag,1982.

37A35,37B40

A

1674-5647(2017)04-0327-13

10.13447/j.1674-5647.2017.04.05

date:March 23,2016.

The NSF(11471114,11671208,11431012 and 11271191)of China and the National Basic Research Program(2013CB834100)of China(973 Program).

*Corresponding author.

E-mail address:030130119@mail.ecust.edu.cn(Ding D D),xianfengma@gmail.com(Ma X F).