Signed Roman(Total)Domination Numbers of Complete Bipartite Graphs and Wheels

ZHAO YAN-cAIAND MIAO LIAN-YING

(1.Department of Basic Science,Wuxi City College of Vocational Technology,Wuxi,Jiangsu,214153)

(2.College of Mathematics,China University of Mining and Technology,Xuzhou,Jiangsu,221116)

Signed Roman(Total)Domination Numbers of Complete Bipartite Graphs and Wheels

ZHAO YAN-cAI1AND MIAO LIAN-YING2

(1.Department of Basic Science,Wuxi City College of Vocational Technology,Wuxi,Jiangsu,214153)

(2.College of Mathematics,China University of Mining and Technology,Xuzhou,Jiangsu,221116)

Communicated by Du Xian-kun

signed Roman domination,signed total Roman domination,complete bipartite graph,wheel

1 Introduction

For notation and graph theory terminology,we in general follow[1].Specifically,let G be a graph with vertex set V(G)=V of order|V|=n(G)and size|E(G)|=m(G),and let v be a vertex in V.The open neighborhood of v is N(v)={u∈V|uv∈E}and the closed neighborhood of v is N[v]={v}∪N(v).The degree of v is d(v)=|NG(v)|.A stable set inG is a set of vertices such that there is no edge between two vertices of the set.A complete bipartite graph is a graph such that its vertices can be partitioned into two stable sets,and every vertex in each stable set has an edge with every vertex in the other.A wheel Wn+1is a graph composed with a cycle Cnand a single vertex c such that c is connected by an edge with every vertex of Cn.

Cockayne et al.[2]defined a Roman dominating function(RDF,for short)on a graph G=(V,E)to be a function f:V→{0,1,2}satisfying the condition that every vertex v for which f(v)=0 is adjacent to at least one vertex u for which f(u)=2.Roman domination has been extensively studied in,for example,[3]–[9].

Ahangar et al.[10]defined a signed Roman dominating function(SRDF)on a graph G=(V,E)to be a function f:V→{−1,1,2}satisfying the conditions that(i)f[v]≥1 for every v∈V,and(ii)every vertex v for which f(v)=−1 is adjacent to a vertex u for which f(u)=2.The signed Roman domination number,denoted by γsR(G),is the minimum weight among all SRDFs in G,that is,

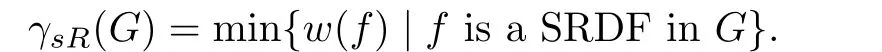
A SRDF of weight γsR(G)is called a γsR(G)-function.

Volkmann[11]further induced a signed total Roman dominating function(STRDF)on a graph G=(V,E)to be a function f:V→{−1,1,2}satisfying the conditions that(i)f(N(v))≥1 for every v∈V,and(ii)every vertex v for which f(v)=−1 is adjacent to a vertex u for which f(u)=2.The signed total Roman domination number,denoted by γstR(G),is the minimum weight among all STRDFs in G,that is,

A STRDF of weight γstR(G)is called a γstR(G)-function.

The exact values of signed Roman(res.signed total Roman)domination number of complete graphs,cycles and paths were given in[10](res.in[11]).In the present paper,we compute the exact values of signed(res.signed total)Roman domination numbers of complete bipartite graphs and wheels.

2 Complete Bipartite Graphs

In[10],the signed Roman domination number of a complete graph has been determined.Now,we provide the signed Roman domination number of a complete bipartite graph as follows.

Theorem 2.1For any complete bipartite graph Km,n(m≤n),

(2)γsR(K2,n)=3;

(3)γsR(K3,n)=4;

(4)For 4≤m≤n,γsR(Km,n)=4.

Proof.We only prove(3)and(4).One can easily obtain similar proofs of(1)and(2)from that of(3).For convenience,we denote the two partitions of V(Km,n)by U={u1,u2,···,um}and V={v1,v2,···,vn}.

First consider(3).Suppose that f is a signed Roman dominating function of K3,n.Since f[v]=f(v)+f(U)≥1 for any v∈V,we have f(U)≥−1.Similarly,f(V)≥−1.

If f(U)=−1,then from f[v]=f(v)+f(U)≥1 we know that f(v)=2 for every v∈V.It follows that

If f(U)=0,then from f[v]=f(v)+f(U)≥1 we know that f(v)≥1 for every v∈V.On the other hand,since f(U)=0,there must be some u∈U such that f(u)=−1,and thus there must be some v∈V such that f(v)=2.Therefore,

If f(U)=1,then by similar arguments to that for the case f(U)=0 we still have w(f)≥4.

If f(U)=2,then there must be some u∈U such that f(u)=−1,and thus from f[u]=f(u)+f(V)≥1 we know that f(V)≥2.Therefore,

If f(U)=3,then the three vertices in U must take values 2,2,−1,respectively,or all take value 1.If the three vertices in U take values 2,2,−1,we suppose that f(u)=−1.Then from f[u]=f(u)+f(V)≥1 we know that f(V)≥2.It follows that

If the three vertices in U all take value 1,then there is no vertex in V taking value−1,and thus w(f)≥4.It is impossible for f(U)=4.If f(U)≥5,then,since f(V)≥−1,we still have w(f)=f(U)+f(V)≥4.In each case we have

Now we construct a signed Roman dominating function f of K3,nsuch that w(f)=4.First let the three vertices in U take values 2,1,−1,respectively.If n is odd,then let f(v1)=2 and assign other vertices in V by 1 and−1 alternately.If n is even,then let f(v1)=f(v2)=2,f(v3)=f(v4)=−1,and assign other vertices in V by 1 and−1 alternately.It is easy to see that w(f)=4 in each case.

Now consider(4).Suppose that f is a signed Roman dominating function of Km,n.If there are vertices with value−1 in none of the two partitions,then w(f)≥m+n≥8.If there are vertices with value−1 in exact one partition,assume without loss of generality that u∈U such that f(u)=−1.Then there must be a vertex v∈V such that f(v)=2.By the condition f[v]=f(v)+f(U)≥1 we have

It follows that

If there are vertices with value−1 in both partitions,then let u∈U and v∈V such that f(u)=f(v)=−1.By the condition f[v]=f(v)+f(U)≥1,we have

Similarly,

It follows that

Therefore,

Now we construct a signed Roman dominating function f such that w(f)=4.

If both m and n are even,then let f(u1)=f(u2)=2,f(u3)=f(u4)=−1,and assign other vertices in U by 1 and−1 alternately;let f(v1)=f(v2)=2,f(v3)=f(v4)=−1,and assign other vertices in V by 1 and−1 alternately.

If both m and n are odd,then let f(u1)=2,and assign other vertices in U by 1 and−1 alternately;let f(v1)=2,and assign other vertices in V by 1 and−1 alternately.

If m is even and n is odd,then let f(u1)=f(u2)=2,f(u3)=f(u4)=−1 and assign other vertices in U by 1 and−1 alternately;let f(v1)=2 and assign other vertices in V by 1 and−1 alternately.

If m is odd and n is even,the construction of f is similar by the symmetry.

In each case,w(f)=4,and thus we finish the proof of Theorem 2.1.

In[11],the signed total Roman domination numbers of a complete graph and a complete bipartite graph Kn,nhave been given.Now,we compute the signed total Roman domination number of a general complete bipartite graph Km,nas follows.

Theorem 2.2For any complete bipartite graph Km,n(m≤n),

(1)if m=n=1,then γstR(Km,n)=2;

(2)if m=1,n=2,then γstR(Km,n)=3;

(3)if m=1,n=3,then γstR(Km,n)=3;

(4)if m=1,n≥4,then γstR(Km,n)=3;

(5)if m=2,n=2,then γstR(Km,n)=2;

(6)if m=2,n=3,then γstR(Km,n=3;

(7)if m=2,n≥4,then γstR(Km,n)=2;

(8)if m=3,n=3,then γstR(Km,n)=4;

(9)if m=3,n≥4,then γstR(Km,n)=3;

(10)if m≥4,then γstR(Km,n)=2.

Proof.For convenience,we denote the two partitions of V(Km,n)(m≤n)by U={u1,u2,···,um}and V={v1,v2,···,vn}.The results in cases(1)–(6)are easy to be verified.In fact,the function f such that f(u1)=f(v1)=1 is a minimum signed total Roman dominating function with w(f)=2 for the case(1);the function f such that f(u1)=2,f(v1)=2,f(v2)=−1 is a minimum signed total Roman dominating function with w(f)=3 for the case(2);the function f such that f(u1)=2,f(v1)=f(v2)=1,f(v3)=−1 is a minimum signed total Roman dominating function with w(f)=3 for the case(3).

For the case(4),we consider two subcases.

(4)aif n is even,then the function f such that f(u1)=2,f(v1)=2,f(vi)=(−1)i−1for i=2,3,···,n is a minimum signed total Roman dominating function with w(f)=3.

(4)bif n is odd,then the function f such that f(u1)=2,f(v1)=f(v2)=1,f(vi)=(−1)ifor i=3,4,···,n is a minimum signed total Roman dominating function such that w(f)=3.

The function f such that f(u1)=2,f(u2)=−1,f(v1)=2,f(v2)=−1 is a minimum signed total Roman dominating function for the case(5);the function f such that f(u1)=2,f(u2)=−1,f(v1)=2,f(v2)=1,f(v3)=−1 is a minimum signed total Roman dominating function for the case(6).

Now consider the case(7).If f is a γstR-function,then

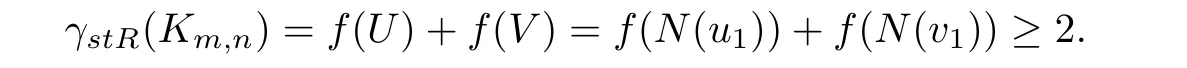
On the other hand,we construct a signed total Roman dominating function with weight 2.We consider two subcases.

(7)aif n is even,then the function f such that f(u1)=2,f(u2)=−1,f(v1)=2,f(vi)=(−1)i−1for i=2,3,···,n is a signed total Roman dominating function with weight 2.

(7)bif n is odd,then the function f such that f(u1)=2,f(u2)=−1,f(v1)=f(v2)=2,f(v3)=f(v4)=−1,f(vi)=(−1)ifor i=5,···,n is a signed total Roman dominating function with weight 2.

For the case(8),it is easy to verify that the function f such that f(u1)=2,f(u2)=1,f(u3)=−1,f(v1)=2,f(v2)=1,f(v3)=−1 is a minimum signed total Roman dominating function with weight 3.

Now consider the case(9).If f is a γstR-function,then first note the fact that

Also it is easy to observe the facts that(i)in both parts there is a vertex with value−1,and thus in both parts there is a vertex with value 2,and(ii)f(U)=f(N(V1))≥1 and f(V)=f(N(u1))≥1.Therefore,w(f)=2 if and only if f(U)=f(V)=1.However,it is easy to observe that f(U)/=1 because of the facts(i),(ii)and|U|=3.So

On the other hand,we first define f(u1)=2,f(u2)=1,f(u3)=−1.Then for even n we define f(v1)=2,f(vi)=(−1)i−1,i=2,3,···,n;for odd n we define f(v1)=2,f(v2)=f(v3)=−1,f(vi)=(−1)i−1,i=4,···,n.It is easy to see that w(f)=3,and thus the desired result.

At last consider the case(10).Let f be a γstR-function.Then

On the other hand,we construct a signed total Roman dominating function f such that w(f)=2.

If m is even,then let f(u1)=2,f(u2)=−1,f(ui)=(−1)ifor i=3,···,m;

if m is odd,then let f(u1)=f(u2)=2,f(u3)=f(u4)=−1,f(ui)=(−1)ifor i=5,···,m;

if n is even,then let f(v1)=2,f(v2)=−1,f(vi)=(−1)ifor i=3,···,n;

if n is odd,then let f(v1)=f(v2)=2,f(v3)=f(v4)=−1,f(vi)=(−1)ifor i=5,···,n.

It is easy to verify that f is a signed total Roman dominating function with weight 2.This completes the proof of Theorem 2.2.

3 Wheels

We first compute the signed Roman domination number of a wheel.

Theorem 3.1For a wheel Wn+1(n≥5),γsR(Wn+1)=1.

Proof.Suppose that the center vertex is c,and the vertices on the cycle C is v1,v2,···,vn.Let f be a γsR-function.First note that if f(c)/=2 then there must exist some vertex with value−1 on the cycle C,and thus there is some vertex with value 2 on C.For otherwise,

contradicting the signed Roman dominating function with weight 1 constructed later.When f(c)/=2,we assume that f(vi)=2.If f(c)=−1,then it is easy to see that the function g such that g(c)=2,g(vi)=−1 and g(x)=f(x)for any other vertex x is still a γsR-function.If f(c)=1,then it is also easy to see that the function g such that g(c)=2,g(vi)=1 and g(x)=f(x)for any other vertex x is still a γsR-function.So we always assume that f(c)=2 throughout the whole proof.

Since f(c)=2 and f[c]=f(c)+f(N(c))≥1,we have

Now we assign the function values of f to the vertices on C as follows.When n≡0(mod 3),let the function values of the first three vertices(by the order of v1,v2,···,vn)be−1,1,−1,and let the function values of the other vertices be−1,2,−1 alternatively.When n≡1(mod 3),let the function values of the first seven vertices be 1,−1,−1,1,−1,1,−1,and let the function values of the other vertices be−1,2,−1 alternatively.When n≡2(mod 3),let the function values of the first five vertices be 1,−1,−1,1,−1,and let the function values of the other vertices be−1,2,−1 alternatively.It is not difficult to verify that the function f in each case is a signed Roman dominating function of Wn+1with w(f)=1.This completes the proof of Theorem 3.1.

Now we compute the signed total Roman domination number of a wheel.

Theorem 3.2For a wheel Wn+1(n≥5),

Proof.Suppose that the center vertex is c,and the vertices on the cycle C are v1,v2,···,vn.Let f be a γstR-function.If f(c)=−1,then there must exist some vertex visuch that f(vi)=2.Then it is easy to see that the function g such that g(c)=2,g(vi)=−1 and g(x)=f(x)for any other vertex x is still a γstR-function.If f(c)=1,then there must exist some vertex with value−1 on the cycle C,and thus there is some vertex visuch that f(vi)=2.For otherwise,

contradicting the signed total Roman dominating function with weight 3 or 4 constructed later.Then it is also easy to see that the function g such that g(c)=2,g(vi)=1 and g(x)=f(x)for any other vertex x is still a γstR-function.So we always assume that f(c)=2 throughout the whole proof.

Since f(c)=2,we have

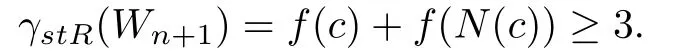
We also have the following claim,which is useful for constructing a minimum signed total Roman dominating function of Wn+1.

Claim 3.1A function f:V(Wn+1)→{−1,1,2}is a signed total Roman dominating function of Wn+1if and only iffor every i=1,2,···,n,where the subscribes(1−1)and(n+1)mean n and 1,respectively.

Proof.Suppose that f is a signed total Roman dominating function of Wn+1.Sinceand f(c)=2,we have

and thus

Conversely,if f:V(Wn+1)→{−1,1,2}is a function such that f(vi−1)+f(vi+1)≥0 for every i=1,2,···,n,then we can easily verify that f is a signed total Roman dominating function of Wn+1.

Now we join each pair of vertices vi−1and vi+1with a broken edge(see Fig.3.1 for example).Then Claim 3.1 means that the two end points of each broken edge must not be both assigned value−1.If n is odd,that is,n≡1,3(mod 4),it is easy to observe that the broken edges induce an odd cycle,say C′=u1u2···un(see the left graph in Fig.3.1 for example).Then by Claim 3.1,the function f such that(together with f(c)=2)is a signed total Roman dominating function of Wn+1with w(f)=3.Noting γstR(Wn+1)≥3,we have

Fig.3.1 Cycles of five and six vertices

If n≡0(mod 4),then we construct a function f such that

It is easy to verify that the above function f(together with f(c)=2)is a signed total Roman dominating function of Wn+1with weight 3.It follows that

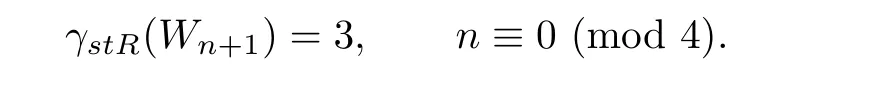
Claim 3.2For odd k,if a function g:V(Ck)→{−1,1,2}satis fies the condition that the two end points of each edge are not both assigned value−1,then w(g)≥1.

Thus by Claim 3.2,

On the other hand,we construct a function f as follows:

It is easy to see that the above function f(together with f(c)=2)is a signed total Roman dominating function of Wn+1with w(f)=4.This means that

We thus complete the proof of Theorem 3.2.

[1]Haynes T W,Hedetniemi S T,Slater P J.Fundamentals of Domination in Graphs.New York:Marcel Dekker,Inc.,1998.

[2]Cockayne E J,Dreyer Jr P A,Hedetniemi S M,Hedetniemi S T.Roman domination in graphs.Discrete Math.,2004,278:11–22.

[3]Atapour M,Sheikholeslami S M,Volkmann L.Global Roman domination in trees.Graphs Combin.,2015,31(4):813–825.

[4]Chambers W,Kinnersley B,Prince N,West D B.Extremal problems for Roman domination.SIAM J.Discrete Math.,2009,23:1575–1586.

[5]Liu C H,Chang G J.Roman domination on strongly chordal graphs.J.Comb.Optim.,2013,26:608–619.

[6]Chellali M,Haynes T W,Hedetniemi S M,Hedetniemi S T,McRae A A.A Roman domination chain.Graphs Combin.,2016,32(1):79–92.

[7]Alvarado J D,Dantas S,Rautenbach D.Averaging 2-rainbow domination and Roman domination.Discrete Appl.Math.,2016,205:202–207.

[8]Roushini L P P,Padmapriea S.Global Roman domination in graphs.Discrete Appl.Math.,2016,200:176–185.

[9]Samodivkin V.Roman domination with respect to nondegenerate graph properties:vertex and edge removal.Australas.J.Combin.,2015,63:41–57.

[10]Ahangar H A,Henning M A,L¨owenstein C,Zhao Y C,Samodivkin V.Signed Roman domination in graphs.J.Comb.Optim.,2014,27(2):241–255.

[11]Volkmann L.Signed total Roman domination in graphs.J.Comb.Optim.,2016,32:855–871.

05C69

A

1674-5647(2017)04-0318-09

10.13447/j.1674-5647.2017.04.04

date:June 13,2016.

The NSF(11271365)of China,and the NSF(BK20151117)of Jiangsu Province.

E-mail address:zhaoyc69@126.com(Zhao Y C).