Existence of Solutions to a p-Laplacian Equation with Integral Initial Condition

SONG WEN-jING,CAO CHUN-LINGAND ZHAO ZHI-QIANG

(1.Institute of Applied Mathematics,Jilin University of Finance and Economics,Changchun,130117)

(2.School of Mathematics,Jilin University,Changchun,130012)

(3.No.11 High School of Changchun,Changchun,130000)

Existence of Solutions to a p-Laplacian Equation with Integral Initial Condition

SONG WEN-jING1,CAO CHUN-LING2AND ZHAO ZHI-QIANG3

(1.Institute of Applied Mathematics,Jilin University of Finance and Economics,Changchun,130117)

(2.School of Mathematics,Jilin University,Changchun,130012)

(3.No.11 High School of Changchun,Changchun,130000)

Communicated by Gao Wen-jie

In this paper,a class of one-dimension p-Laplacian equation with nonlocal initial value is studied.The existence of solutions to such a problem is obtained by using the topological degree method.

integral initial condition,existence,topological

1 Introduction

Boundary value problems with integral boundary conditions in the ordinary differential equations arise in different areas of applied mathematics and physics.For example,heat conduction,chemical engineering,underground water flow,thermo-elasticity and plasma physics can be reduced to nonlocal problems with integral boundary conditions.For boundary-value problems with integral boundary conditions and comments on their importance,we refer the readers to[1]–[4]and the references therein.For more information about the general theory of integral equations and their relation with boundary-value problems,readers may refer to[5]–[7].

In recent years,the existence and multiplicity of positive solutions for nonlocal problems have attracted great attention to many mathematicians.Readers may refer to[8]–[15]and references therein.On the other hand,initial-value problems with integral conditions constitute a very interesting and important class of problems.The integral initial valueproblems to one-dimension p-Laplacian equation are meaningful in mathematics and physics.

The purpose of this paper is to investigate the existence of solutions to the following one-dimension p-Laplacian equation:

with integral initial value

where

The paper is organized as follows.In Section 2,we provide some necessary preliminaries and in Section 3 the main result is stated and proved.

2 Preliminaries

Let I be the real interval[0,1]and C(I)be the Banach space of all continuous functions u:I→R,equipped with the norm

for any u∈C(I).

Consider the following problem:

where

Integrating(2.1)from 0 to t,we obtain

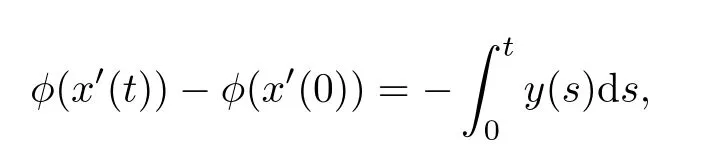
and by using the initial condition(2.3),we have

Integrating the above equality from 0 to t again,we obtain

Let

define an operator K:C(I)→C(I)by

then(2.4)can be rewritten as

Thus x(t)is a solution to(2.1)–(2.3)if and only if it is a solution to(2.5).

Lemma 2.1I−K is a Fredholm operator.

Proof.To prove that I−K is a Fredholm operator,we need only to show that K is completely continuous.

It is easy to see from the definition of K that K is a bounded linear operator from C(I)to C(I).Obviously,dimR(K)=1.So K is a completely continuous operator.This completes the proof.

Lemma 2.2(Alternative Theorem)Suppose that X is a Banach space and A is a completely continuous operator from X to X.Then for any λ/=0,only one of the following statements holds:

(i)For any y∈X,there exists a unique x∈X,such that

(ii)There exists an x∈X,x/=0 such that

Lemma 2.3The problem(2.1)–(2.3)admits a unique solution.

Proof.Since the problem(2.1)–(2.3)is equivalent to the problem(2.5),we need only to show that the problem(2.5)has a unique solution.

By using Lemma 2.1 and alternative theorem,it is sufficient for us to prove that

has only a trivial solution

On the contrary,suppose(2.6)has a nontrivial solution µ,thenµis a constant,and we have

The definition of K and the above equality yield to

which is contradictory to the assumptions

and

Thus we complete the proof.

3 Main Results

Throughout this section,we assume that the following conditions hold:

From Lemma 2.3 we know that u(t)is a solution to the problem(1.1)–(1.3)if and only if it is a solution to the following integral equation:

C1(I)denotes the Banach space with the norm

for any u∈C1(I).

define an operator T:C1(I)→C1(I)by

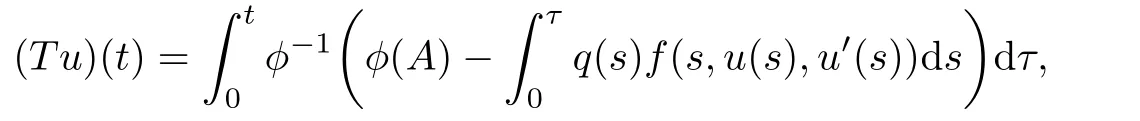
then(3.1)can be rewritten as

In order to prove the existence of solutions to(3.1),we need the following lemmas.

Lemma 3.1T is completely continuous.

Proof.For any ball B1={u∈C1(I);‖u‖1≤R1},set

Then we have for any u∈B1,

This shows that T(B1)is uniformly bounded.

Since f:[0,1]×R×R→R is continuous,it is uniformly continuous on[0,1]×[−R1,R1]×[−R1,R1]and satisfies condition(H2).Thus for any ε＞0,there exists a δ＞0 such that for all t1,t2∈[0,1],|t1−t2|＜δ,we have

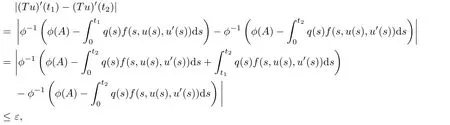
where ϕ−1is uniformly continuous,which implies that T(B1)is equicontinuous on[0,1].Therefore,T:C1(I)→C1(I)is completely continuous.This completes the proof of Lemma 3.1.

Theorem 3.1Assume that the conditions(H1)–(H4)hold.Then(1.1)–(1.3)admits at least one solution.

Proof.Lemmas 2.1 and 3.1 imply that the operator K+T is completely continuous on C1(I).It suffices for us to prove the following equation

has at least one solution.

define H:[0,1]×C1[0,1]→C1[0,1]as

and it is clear that H is completely continuous.

Set

Then we have

To apply the Leray-Schauder degree for hσ,we need only to show that there exists a ball BR(θ)in C1[0,1]whose radius R will be fixed later,such that θ/∈hσ(∂BR(θ)).

Choose

Then for any fixed u∈∂BR(θ),there exists a t0∈[0,1]such that

or

If|u(t0)|=R,a direct calculation leads to

From(H4),we have

This implies hσu/=θ,and hence θ/∈hσ(∂BR(θ)).

Similarly,if|u′(t0)|=R,by directly calculating,we have

This implies hσu/=θ,and hence θ/∈hσ(∂BR(θ)).

Since

we know that(3.2)admits a solution u∈BR(θ),which implies that(1.1)–(1.3)also admit a solution in BR(θ).

[1]Boucherif A.Second-order boundary value problems with integral boundary conditions.Nonlinear Anal.,2009,70:364–371.

[2]Gallardo J M.Second order differential operators with integral boundary conditions and generation of semigroups.Rocky Mountain J.Math.,2000,30:1265–1292.

[3]Khan R A.The generalized method of quasilinearization and nonlinear boundary value problems with integral boudary conditions.Electron.J.Qual.Theory Differ.Equ.,2003,10:1–15.

[4]Lomtatidze A,Malaguti L.On a nonlocal boundary-value problems for second order nonlinear singular differential equations.Georgian Math.J.,2000,7:133–154.

[5]Agarwal R P,O’Regan D.In finite Interval Problems for differential.Difference and Integral Equations.Dordtreht:Kluwer Academic Publishers,2001.

[6]Corduneanu C.Integral Equations and Applications.Cambridge:Cambridge University Press,1991.

[7]Guo D J,Lakshmikantham V,Liu X Z.Nonlinear Integral Equations in Abstract Spaces,Dordrecht:Kluwer Academic Publishers,1996.

[8]Chen S H,Hu T,Chen L,Wang C.Existence results for n-point boundary value problem of second order ordinary differential equations.J.Comput.Appl.Math.,2005,180:425–432.

[9]Feng M Q,Ge W G.Positive solutions for a class of m-point singular boundary value problems.Math.Comput.Modelling,2007,46:375–383.

[10]Feng M Q,Ji D H,Ge W G.Positive solutions for a class of boundary-value problem with integral boundaty conditions in Banach spaces.J.Comput.Appl.Math.,2008,222:351–363.

[11]Ionkin N I.Solution of a boundary value problem in heat conduction theory with nonlocal boundary conditions.differential Equations,1977,13:294–304.

[12]Wang H Y.On the mumber of positive solutions of nonlinear systems.J.Math.Anal.Appl.,2003,281:287–306.

[13]Wei Z,Pang C.Positive solutions of some singular m-point boundary value problems at nontesonance.Appl.Math.Comput.,2005,171:433–449.

[14]Yang Z.Positive solutions of a second order integral boundary value problem.J.Math.Anal.Appl.,2006,321:751–765.

[15]Zhang X M,Feng M Q,Ge W G.Symmetric positive solutiongs for p-Laplacian fourth order differential equations with integral boundary conditions.J.Comput.Appl.Math.,2008,222:561–573.

34B15,37C25

A

1674-5647(2017)04-0304-07

10.13447/j.1674-5647.2017.04.02

date:May 30,2016.

The NSF(11271154 and 11326103)of China,Research Project(2014164)of the Education of Jilin Province,and the Youth Studies Program(XJ2012006)of Jilin University of Finance and Economics.

E-mail address:swj-78@163.com(Song W J).