A New Hybrid Algorithm and Its Numerical Realization for a Quasi-nonexpansive Mapping

GAO XING-HUI AND MA LE-RONG

(College of Mathematics and Computer Science,Yan’an University,Yan’an,Shaanxi,716000)

A New Hybrid Algorithm and Its Numerical Realization for a Quasi-nonexpansive Mapping

GAO XING-HUI AND MA LE-RONG

(College of Mathematics and Computer Science,Yan’an University,Yan’an,Shaanxi,716000)

Communicated by Ji You-qing

The purpose of this article is to propose a new hybrid projection method for a quasi-nonexpansive mapping.The strong convergence of the algorithm is proved in real Hilbert spaces.A numerical experiment is also included to explain the effec-tiveness of the proposed methods.The results of this paper are interesting extensions of those known results.

quasi-nonexpansive mapping,hybrid algorithm,strong convergence,Hilbert space

1 Introduction

Suppose that H is a real Hilbert space.We denote by〈·,·〉and‖·‖the inner product and the norm,respectively.Suppose that C is a closed convex nonempty subset of H.We denote by F(T)the fixed point set of a mapping T:C→C,i.e.,F(T)={x∈C:x=Tx}.A mapping T:C→C is called a nonexpansive mapping if

A mapping T:C→C is called a quasi-nonexpansive mapping if F(T)/=∅such that

Obviously,a nonexpansive mapping with a nonempty fixed point set F(T)is a quasinonexpansive mapping,but the converse may be not true.

The construction of fixed points for nonlinear mappings is of practical importance.In particular,iterative algorithms for finding fixed points of nonexpansive mappings have received extensive investigation(see[1]–[2])since these algorithms have a variety of applications in inverse problem,image recovery and signal processing(see[3]–[5]).

Nakajo and Takahashi[6]first introduced a hybrid algorithm for a nonexpansive mapping.Thereafter,some hybrid algorithms have been studied extensively since they have strong convergence(see[7]–[13]).Recently,Dong and Lu[14]proposed the following hybrid iterative method for a nonexpansive mapping in a Hilbert space H and gave numerical examples to describe the effectiveness of the new algorithm:

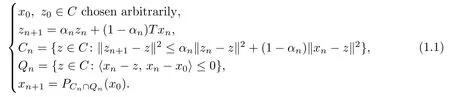
Dong and Lu[14]showed the following theorem.

On the basis of[14],we design a simple hybrid method for a quasi-nonexpansive mapping.A strong convergence theorem is proved by using new methods in this paper.We also give a numerical experiment to describe the effectiveness of the proposed algorithm.The results of this paper improve the related ones obtained by some authors(e.g.,[6]and[14],etc.).

2 Preliminaries

Lemma 2.1[8]Let K be a closed convex subset of real Hilbert space H.Given x∈H and z∈K.Then z=PKx if and only if there holds the relation

Lemma 2.2[14]Suppose that{an}and{bn}are nonnegative real sequences,α∈[0,1),β∈R+,and for any n∈N,the following inequality holds:

Lemma 2.3Let C be a closed convex nonempty subset of H,T:C→C be a quasinonexpansive mapping.Then F(T)is a convex closed subset of C.

Proof.We prove first that F(T)is closed.Let{pn}⊂F(T)with pn→p(n→∞).We prove that p∈F(T).Since T is quasi-nonexpansive,one has

which implies that pn→Tp as n→∞.Then p=Tp.So p∈F(T).

Next we show that F(T)is convex.For arbitrary p1,p2∈F(T),t∈(0,1),taking p3=tp1+(1−t)p2,we show that p3∈F(T).Indeed,we have

This implies that Tp3=p3.

Lemma 2.4Let C be a closed convex nonempty subset of H.Suppose that PCis the projection from H onto C.Then

Proof.The conclusion of this lemma can be obtained by the proof process of Lemma 3.3 in[6],or by using Lemma 2.1 in this paper.

3 Main Results

Proof.By Lemma 2.3 and the condition F(T)/=∅,one knows thatis well defined for any x0∈C.It follows from the constructions of Cnthat for n≥1,Cnis closed and convex.We omit the details.

Step 1Show that F(T)⊂Cn,n≥1.

In fact,for n=1,F(T)⊂C1=C.Assume that F(T)⊂Cnfor some n≥1.For any p∈F(T)⊂Cn,from(3.1),one has

which implies p∈Cn+1.Therefore,F(T)⊂Cn,n≥1.

In view of(3.1),one has xn=PCn(x0).Since Cn+1⊂Cnand xn+1∈Cn+1for all n≥1,one has

On the other hand,as F(T)⊂Cnby Step 1,it follows that

Combining(3.2)and(3.3),we obtain thatexists.

Step 3Show that xn→q(n→∞),q∈C.

Taking m,n→∞in(3.4),one gets xm−xn→0 as m,n→∞,which proves that{xn}is a Cauchy sequence in C.By completeness of H and closedness of C,one can assume that xn→q as n→∞.

Step 4Show that xn−Txn→0(n→∞).

Since xn→q as n→∞,one has

Since xn+1∈Cn+1,one has

For this reason,we have

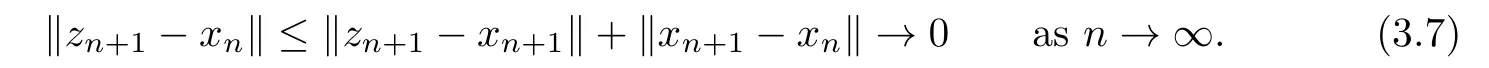
Noting that

we get

Since αn≤σ and by(3.6)and(3.7),we have

Step 5Show that

From Step 3,we know that xn→q as n→∞.In view of(3.8)and closedness of T,we obtain q=Tq.So q∈F(T).Noting that F(T)⊂Cnand xn=PCnx0,by Lemma 2.1,we conclude that

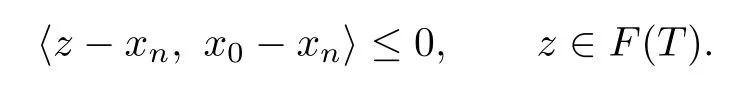
It follows that

Remark 3.1Theorem 3.1 generalizes Theorem 1.1 as follows:

(i)Nonexpansive mappings are extended to quasi-nonexpansive mappings.

(ii)Algorithm(3.1)is more simple than algorithm(1.1),that is,removing the set Qn.

Changing the definitions of zn+1and Cnin algorithm(3.1),we have the following theorem.

The proof of Theorem 3.2 is similar to Theorem 3.1 and omitted here.

Remark 3.2Theorem 3.2 generalizes the Theorem 3.2 of[14]as follows:

(i)Nonexpansive mappings are extended to quasi-nonexpansive mappings.

(ii)Algorithm(3.9)is more simple than ones used in Theorem 3.2 of[14],that is,removing the set Qn.

4 Numerical Experiments

We provide some numerical examples to show our algorithms are effective.In the numerical experiments,taking the mapping T:C→R by

where C=[0,2π],R denotes the set of real numbers.Noting that F(T)={0}and T is a quasi-nonexpansive mapping,but it is not a nonexpansive mapping.The algorithm(3.1)iterates 50 steps.

For algorithm(3.1),putting αn=0.1,βn=0.1,γn=0.9,σ=0.1.Choosing x0,z0∈[0,2π]arbitrarily,then for 50 pairs of Different initial values,we can see that all the sequences{xn}are convergent in Fig.4.1 and all the sequences{zn}are convergent in Fig.4.2.

Fig.4.1 The iterative curves of{xn}in algorithm(3.1)under Different initial values

Fig.4.2 The iterative curves of{zn}in algorithm(3.1)under Different initial values

5 Conclusions

A kind of hybrid algorithm of a quasi-nonexpansive mapping was introduced in this paper.Its strong convergence has been proven in Hilbert spaces.We also have given a numerical example to explain the effectiveness of the introduced algorithm.

[1]Chang S S.Viscosity approximation methods for a finite family of nonexpansive mappings in Banach spaces.J.Math.Anal.Appl.,2006,323:1402–1416.

[2]Yao Y H.A general iterative method for a finite family of nonexpansive mappings.Nonlinear Anal.,2007,66:2676–2687.

[3]Xu H K.A variable Krasnoselskii-Mann algorithm and the multiple-set split feasibility problem.Inverse Problems,2006,22:2021–2034.

[4]Combettes P L.On the numerical robustness of the parallel projection method in signal synthesis.IEEE Signal Process Lett.,2001,8:45–47.

[5]Podilchuk C I.Mammone R J.Image recovery by convex projections using a least-squares constraint.J.Opt.Soc.Amer.A,1990,7:517–521.

[6]Nakajo K,Takahashi W.Strong convergence theorems for nonexpansive mappings and nonex-pansive semigroups.J.Math.Anal.Appl.,2003,279:372–379.

[7]Kim T H,Xu H K.Strong convergence of modified Mann iterations.Nonlinear Anal.,2005,61:51–60.

[8]Marino G,Xu H K.Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces.J.Math.Anal.Appl.,2007,329:336–346.

[9]Wei L,Cho Y J,Zhou H Y.A strong convergence theorem for common fixed points of two relatively nonexpansive mappings and its applications.J.Appl.Math.Comput.,2009,29:95–103.

[10]Qin X L,Su Y F.Approximation of a zero point of accretive operator in Banach spaces.J.Math.Anal.Appl.,2007,329:415–424.

[11]Zhou H Y.Strong convergence theorems for a family of Lipschitz quasi-pseudo-contractions in Hilbert spaces.J.Math.Anal.Appl.,2009,71:120–125.

[12]Zhou H Y,Su Y F.Strong convergence theorems for a family of quasi-asymptotic pseudo-contractions in Hilbert spaces.Nonlinear Anal.,2009,70:4047–4052.

[13]Liu Y X,Zheng L G,Wang P Y,Zhou H Y.Three kinds of new hybrid projection methods for a finite family of quasi-asymptotically pseudocontractive mappings in Hilbert spaces.Fixed Point Theory Appl.,2015,2015(118):1–13.

[14]Dong Q L,Lu Y Y.A new hybrid algorithm for a nonexpansive mapping.Fixed Point Theory Appl.,2015,2015(37):1–7.

47H05,47H09,47H10

A

1674-5647(2017)04-0340-07

10.13447/j.1674-5647.2017.04.06

date:Dec.29,2016.

The NSF(11071053)of China,Natural Science Basic Research Plan(2014JM2-1003)in Shaanxi Province of China,and Scientific Research Project(YD2016-12)of Yan’an University.

E-mail address:yadxgaoxinghui@163.com(Gao X H).