On the Lower Bound of the Divisibility of Exponential Sums in Binomial Case

LIU XIAO-GANG

(School of Computer Science and Technology,Nanjing Tech University,Nanjing,211800)

On the Lower Bound of the Divisibility of Exponential Sums in Binomial Case

LIU XIAO-GANG

(School of Computer Science and Technology,Nanjing Tech University,Nanjing,211800)

Communicated by Du Xian-kun

In this article,we analyze the lower bound of the divisibility of families of exponential sums for binomials over prime field.An upper bound is given for the lower bound,and,it is related to permutation polynomials.

exponential sum, finite field,binomial,permutation polynomial

1 Introduction

Exponential sums and their divisibility have been applied to characterize important properties of objects in applied mathematics.There are many estimates for the divisibility of exponential sums(see[1]–[5]).It is difficult in general.The exact divisibility of families of exponential sums associated to binomials F(X)=aXd1+bXd2,is computed under some natural conditions when a,b∈F∗p(see[2]).The result is applied to the solutions of equations,to the study of Waring problem over finite fields,and to the determination of permutation polynomials.

Let F(X)be a two terms of polynomial in one variable over prime field Fp.The following bound for the valuation(divisibility)of an exponential sum can be thought of as a particular case of Theorem 8 in[4].

Theorem 1.1LetwithIf Sp(F)is the exponential sumwhereis a solution of the modular equation

Remark 1.1Let Qpbe the p-adic field and ξ be a primitive p-th root of unity indefine θ=1−ξ and denote by νθthe valuation over θ.Note that νθ(p)=p−1 andLet ϕ:Fp→Q(ξ)be the nontrivial additive character defined by ϕ(a)=ξafor a∈Fp.The exponential sum associated to F(X)is defined as

In the next section,Theorem 2.1 is presented on the lower bound in Theorem 1.1,which is less than half of p.To this end,the domain[0,1)is splitted into in finitely many segments,which are used for Different range of integers.In this process,we can make a success in our analysis for every step,which is not enough for the whole.But finally,with the splitting parts changing and interacting with each other,we can make it complete.Though not much long and complicated,the important idea in our work is to note the effect of those seemingly nonsignificant interactions between Different segments.

2 Main Result

Theorem 2.1Let 1≤d1/=d2≤p−2 be positive integers and let p≥5 be a prime.Then

Proof.First,consider the case when d1,d2are odd numbers,and

where gcd denotes the greatest common divisor of two or more integers.

Let i=1.Then d1i+d2j=d1+d2j.If it is zero modular p−1,then j/=p−1;if j=p−2,then d1+d2j=d1+d2(p−2)=d1+d2(p−1)−d2is not equal to zero modular p−1.Also,j/=0.Note that such a j must exist since gcd(d2,p−1)=1.So,

We can find that the union of the sets is[0,1).Assume thatandThen

which implies that by(2.2)

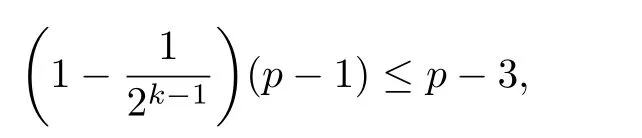
that is,

Thus

Since d1+d2j≡0 mod p−1,we have

and

So,

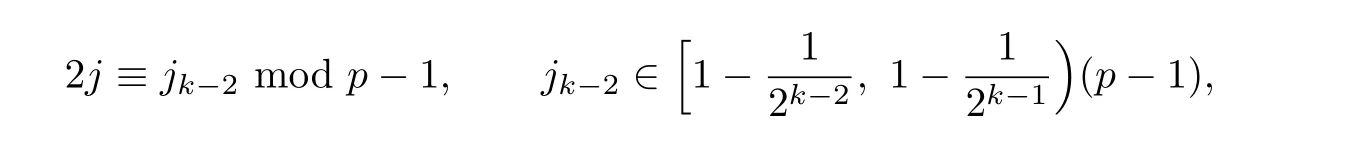
and

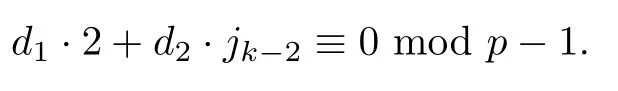
Multiplying both sides of the modular equation by 2 again,and continue in this way by reducing the modular equation as above,we find that

We have that d1,d2are odd numbers and d1+d2is even.And

and

The proof is completed.

Remark 2.1Theorem 2.1 is closely related to permutation polynomials.A permutation polynomial over a finite field is one which permutes the elements of the field.There is the Hermite’s criterion about whether a polynomial is a permutation polynomial.

Theorem 2.2[6],[7]A polynomial F(X)over a finite field Fq(q is a power of prime p)is a permutation polynomial if and only if

(1)for each i with 0＜i＜q−1,the reduction of F(X)imodulo Xq−X has degree less than q−1,and

(2)F(X)has exactly one root in Fq.

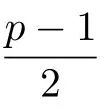
is expanded and reduced,there will be no terms of degree p−1.To see this,assume that

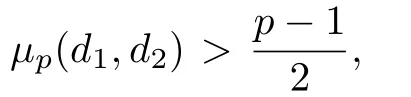
But our result(2.1)implies that such a situation will never happen.That is,generally speaking,the exponents d1,d2cannot be parameterized to satisfy the first condition of Theorem 2.2 by using Roger’s result.

[1]Adolphson A,Sperber S.p-adic estimates for exponential sums and the theorem of Chevalley-Warning.Ann.Sci.Ecole Norm.Sup.,1987,20:545–556.

[2]Castro F,Figueroa R,Medina L.Exact divisibility of exponential sums and some consequences.Contemp.Math.,2012,597:55–66.

[3]Moreno O,Moreno C J.Improvements of the Chevalley-Warning and the Ax-Katz theorems.Amer.J.Math.,1995,1:241–244.

[4]Moreno O,Shum K,Castro F N,Kumar P V.Tight bounds for Chevalley-Warning-Ax type estimates,with improved applications.Proc.London Math.Soc.(3),2004,88:545–564.

[5]Sperber S.On the p-adic theory of exponential sums.Amer.J.Math.,1986,108:255–296.

[6]Dickson L E.The analytic representation of substitutions on a power of a prime number of letters with a discussion of the linear group.Ann.of Math.,1896–1897,11:65–120.

[7]Hermite Ch.Sur les fonctions de sept lettres.C.R.Math.Acad.Sci.Paris,1863,57:750–757.

[8]Rogers L J.Note on functions proper to represent a substitution of a prime number of letters.Messenger Math.,1892,21:44–47.

11L07,12E30

A

1674-5647(2017)04-0359-04

10.13447/j.1674-5647.2017.04.08

date:Aug.22,2016.

The NSF(61502230)of China.

E-mail address:liuxg0201@163.com(Liu X G).