Vector-valued Inequalities for Commutators of Singular Integrals on Herz Spaces with Variable Exponents

WANG LI-WEI,QU MENGAND SHU LI-SHENG

(1.School of Mathematics and Physics,Anhui Polytechnic University,Wuhu,Anhui,241000)

(2.School of Mathematics and Computer Science,Anhui Normal University,Wuhu,Anhui,241003)

Vector-valued Inequalities for Commutators of Singular Integrals on Herz Spaces with Variable Exponents

WANG LI-WEI1,QU MENG2AND SHU LI-SHENG2

(1.School of Mathematics and Physics,Anhui Polytechnic University,Wuhu,Anhui,241000)

(2.School of Mathematics and Computer Science,Anhui Normal University,Wuhu,Anhui,241003)

Communicated by Ji You-qing

Based on the theory of variable exponents and BMO norms,we prove the vector-valued inequalities for commutators of singular integrals on both homogeneous and inhomogeneous Herz spaces where the two main indices are variable exponents.Furthermore,we show that a wide class of commutators generated by BMO functions and sublinear operators satisfy vector-valued inequalities.

variable exponent,Herz spaces,commutator,singular integral

1 Introduction

The modern development of variable exponent function spaces was initiated by Kov´aˇcik and R´akosn´ık[1]appearing in 1991,and was originally tied closely to the theory of fluid dynamics,image restoration and PDE with non-standard growth conditions,for an overview we refer to[2]–[4].On the other hand,function spaces with variable exponents have many properties in common with the classical cases,but they also Differ in surprising and subtle ways.For instance,the variable exponent Lebesgue spaces are not translation invariant.More precisely,if p(·)is non-constant in Rn,then there always exist f∈Lp(·)(Rn)and h∈Rnsuch that f(x+h)is not in Lp(·)(Rn).As a consequence Lp(·)(Rn)spaces are not rearrangement invariant Banach function spaces,and so a great deal of classical machinery is not applicable(see[5]).For this reason,apart from useful application considerations,themotivation to study such spaces has an intrinsic interest.In the past 25 years,especially the past decade,we have witnessed a rapid growth in the study of these and related spaces,see[6]–[13]and references therein.

The classical Herz spaces have been playing an integral role in harmonic analysis and PDE.After they were introduced in[14],the theory of these spaces had a remarkable development in part due to its usefulness in applications.For instance,they are good substitutes of the ordinary Hardy spaces when considering the boundedness of non-translation invariant singular integral operators.They also appear in the summability of Fourier transforms and in the regularity theory for elliptic and parabolic equations in divergence form,see[15]–[18]for example.Recently,defined homogeneous Herz spacesand inhomogeneous Herz spaceswith variable exponent p(·)but fixed α∈R and proved the boundedness of sublinear operators and commutators of singular integrals on those spaces.Somewhat later,Almeida and Drihem[6]introduced the generalized Herz spacesandwhere the exponent α is variable as well.Under natural regularity assumptions on the exponent functions,they showed that many classical operators,such as maximal,potential and Calder´on-Zygmund operators,are bounded on such spaces.

Given a locally integrable function K defined on Rn{0},suppose that the Fourier transform of K is bounded,and K satis fies

Then the singular integral operatordefined byis a bounded operator on the classical Lebesgue spaces Lp(Rn).Let b∈BMO(Rn).define the commutatorto be the operator

A celebrated result of Coifmanet al.[19]states that the operator[b,]is bounded on Lp(Rn)for 1＜p＜∞.Moreover,this commutator has proved to be of interest in many contexts and in particular in the theory of PDE,we shall only mention the recent results in the theory of elliptic equations with discontinuous coefficients(see[20]and[21]).

In[22],Cruz-Uribe et al.showed thatand[b,]are both bounded operators on the variable exponent Lebesgue spaces Lp(·)(Rn).Using the theory of weighted norm inequalities and extrapolation,they also proved some vector-valued inequalities for such operators.A further step was taken by Izuki[23],who established the similar vector-valued estimates for the commutatoron Herz spacesandFrom Remark 2.2 below,one can see that if α(·)is constant,thenandcoincide withandrespectively.Hence,it is of interest to ask whether the vectorvalued inequalities still hold foronandOur first aim in this paper is to give an affirmative answer to the above question.

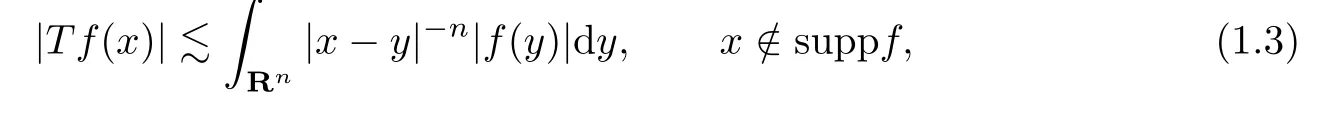
On the other hand,one of the important problems on Herz spaces is boundedness of sublinear operators satisfying the size condition for integrable and compactly supported functions f.We note that the condition(1.3)was initially studied by Soria and Weiss[24]and it is satisfied by several classical operators,such as the Hardy-Littlewood maximal operator,the Carleson maximal operator,Bochner-Riesz means at the critical index and so on.Many studies involving such sublinear operators can be found in the literatures,see[25]and[26]for example.Nevertheless,it is worthing noting the recent paper[27],where the vector-valued inequalities for the sublinear operators T were studied on Herz spacesandSo it is natural to ask what will happen for the commutator[b,T]on such spaces?Another purpose of this paper is to give the similar vector-valued estimates for the commutator[b,T]on Herz spacesand

2 Preliminaries and Lemmas

Given an open set Ω⊂Rn.Let p(·):Ω→[1,∞).The variable exponent Lebesgue space Lp(·)(Ω)is the class of all measurable functions f on Ω such that for some λ＞0,

This set becomes a Banach space when equipped with the norm

Obviously,when p(·)is a constant this immediately reduces to the usual norm on the classical Lebesgue spaces.The spaceis defined by

For simplicity,we denote

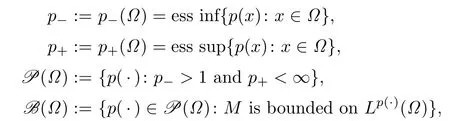
where the Hardy-Littlewood maximal operator M is defined by

definition 2.1Let 0＜q≤∞,p(·)∈P(Rn)and α(·):Rn→R with(1)The homogeneous Herz spaceis defined as the set of allsuch that

(2)The inhomogeneous Herz spaceconsists of allsuch that

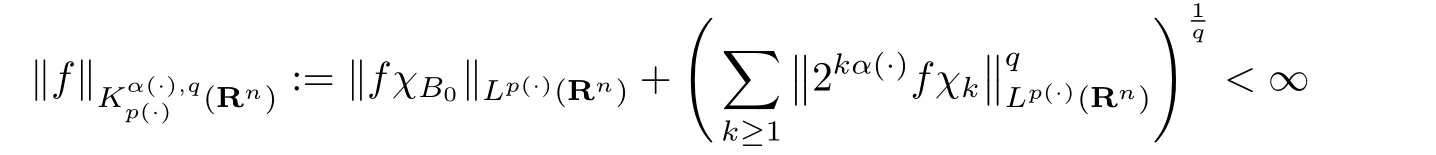
with the usual modi fication when q=∞.

Remark 2.1Clearly,if α(·)is a constant,thenwhich is first defined by Izuki[7].If both α(·)and p(·)are constants,thenare the classical Herz spaces in[17].

A function α(·):Rn→R is called log-H¨older continuous at the origin(or has a log decay at the origin),if there exists a constant Clog＞0 such that

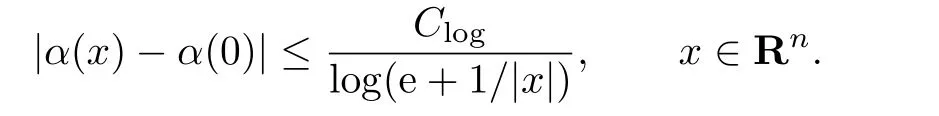
If for some α∞∈R and Clog＞0 there holds that

then α(·)is called log-H¨older continuous at infinity(or has a log decay at the in finity).

Let us denote

for the sequences{hk}k∈Zof measurable functions(with the usual modification when q=∞).

Proposition 2.1[6]Let 0＜q≤∞,p(·)∈P(Rn)and α(·)∈L∞(Rn).If α(·)is log-H¨older continuous both at the origin and at in finity,then

In order to prove our main results,we first introduce some key lemmas.

Lemma 2.1Let p(·)∈P(Rn).If f∈Lp(·)(Rn)and g∈Lp′(·)(Rn),then

Lemma 2.2If 1＜r＜∞,then we have for all sequences of locally integrable functionssatisfying

We remark that Lemmas 2.1 and 2.2 are the well-known generalized H¨older’s inequality and generalized Minkowski inequality,respectively.The following Lemmas 2.3 and 2.4 were shown in[23],and Lemma 2.5 was considered by Cruz-Uribe et al.in[22].

Lemma 2.3Let p(·)∈B(Rn).Then we have that for all balls B in Rn,

Lemma 2.4Let p(·)∈B(Rn).Then we have that for all balls B in Rnand all measurable subsets S⊂B,

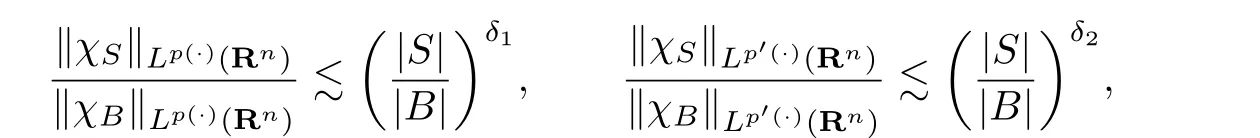
where δ1,δ2are constants with 0＜δ1,δ2＜1.

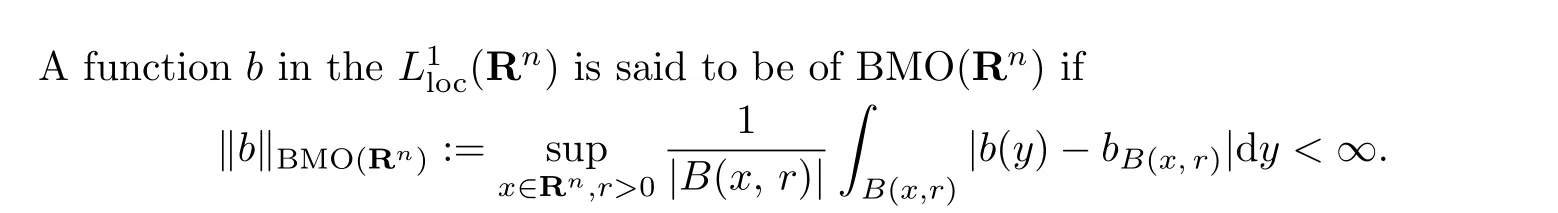
Lemma 2.5Let b∈BMO(Rn),k＞j(k,j∈N).Then we have

and

Lemma 2.6Let b∈BMO(Rn)and p(·)∈B(Rn).Then for all 1＜q＜∞,

and

3 Main Results and Their Proofs

In this section,we prove some vector-valued inequalities on Herz spacesandWe consider only 0＜q＜∞,the arguments are similar in the case q=∞.

Our main results in this paper can be stated as follows.

Theorem 3.1Suppose that b∈BMO(Rn)and p(·)∈B(Rn).Let[b,]be defined as in(1.2),and let 1＜r＜∞,0＜q≤∞,α(·):Rn→R with α(·)∈L∞(Rn)be log-H¨older continuous both at the origin and at infinity,such that−nδ1＜α(0)≤α∞＜nδ2,where

0＜δ1,δ2＜1 are the constants appearing in Lemma 2.4.Then we have the vector-valued inequality

for any locally integrable functions

Remark 3.1Theorem 3.1 extends the main result of Izuki(see[23],Page 206)in the case k=1 to a more general function space.In fact,by using the same method as Theorem 3.1,we can prove the similar results for the case k＞1(see[23],Page 199 for the definition of k-order commutators of the operator).

Furthermore,we obtain the following result.

Theorem 3.2Suppose that b∈BMO(Rn)and p(·)∈B(Rn).Let 1＜r＜∞,0＜q≤∞,α(·):Rn→R with α(·)∈L∞(Rn)be log-H¨older continuous both at the origin and at in finity such that−nδ1＜α(0)≤α∞＜nδ2,where 0＜δ1,δ2＜1 are the constants appearing in Lemma 2.4.If T is a sublinear operator satisfying the size condition(1.3)and its commutator[b,T]satis fies

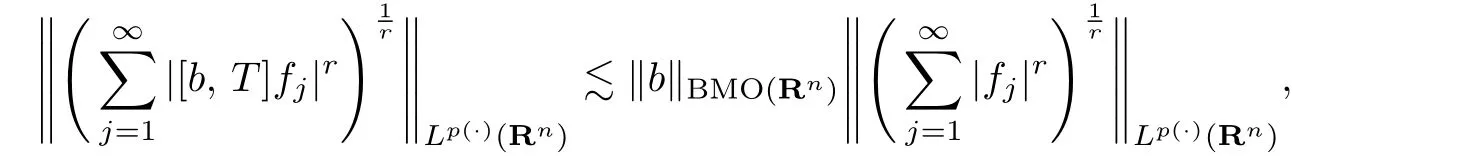
then we have the vector-valued inequality

for any locally integrable functionssatisfying

Remark 3.2There exist some commutators satisfying the above vector-valued inequality on Lp(·)(Rn)provided p(·)∈B(Rn),for instance,commutators of Littlewood-Paley operators and singular integral operators,see[22],[28]–[30]for more details.

Remark 3.3In Theorems 3.1 and 3.2,the same boundedness also holds for inhomogeneous Herz spaces

Proof of Theorem 3.1We only give the proof in the case ofthe inhomogeneous case may be treated in the same way with minor modi fications.

In view of Proposition 2.1,we have

Similarly,we obtain

Thus we get

We first estimate E＜.For each k∈Z,i≤k−2 and a.e.x∈Rk,by Lemma 2.2,we obtain

Thus,we have

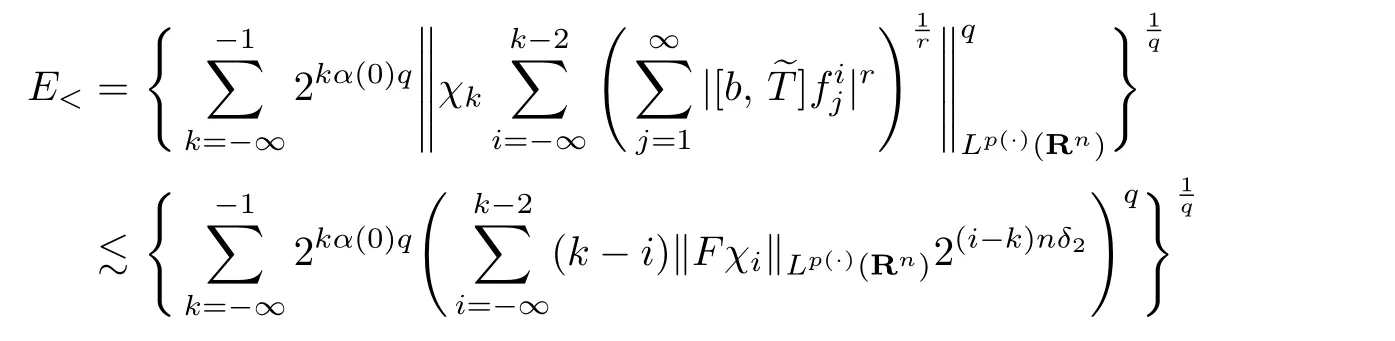
Now we can distinguish two cases as follows.

Case 1.0＜q≤1.

By virtue of the well-known inequality

and nδ2−α(0)＞0,from(3.3),we derive the estimate

Case 2.1＜q＜∞.

In this case,by(3.3)and H¨older’s inequality,we conclude that

For E＞,a simple calculation gives

If 0＜q≤1,noting that α(0)≤α∞＜nδ2,by the Minkowski inequality and(3.4),we get

If 1＜q＜∞,applying H¨older’s inequality,we obtain

Combining the estimates above,we arrive at the desired inequality

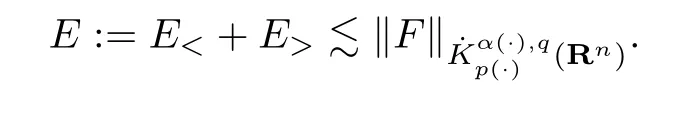
For F,Lemma 2.6 implies that

We proceed now to estimate G.For each k∈Z,i≥k+2 and a.e.x∈Rk,an application of Lemma 2.2 gives

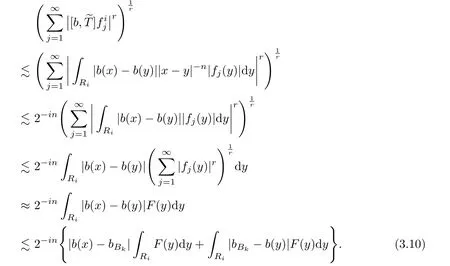
Thus,by virtue of Lemmas 2.4,2.8,2.6 and 2.7 in proper order,we have

Hence,we get

and

For G＞,if 0＜q≤1,in view of nδ1+α∞＞0,once again by(3.4),we have

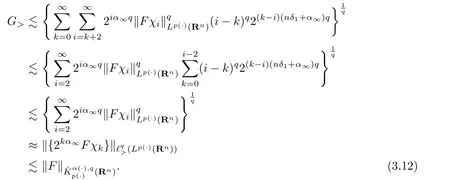
If 1＜q＜∞,H¨older’s inequality yields

After applying the similar arguments used in the estimation of E＞,we can easily get for all 0＜q＜∞,

Thus

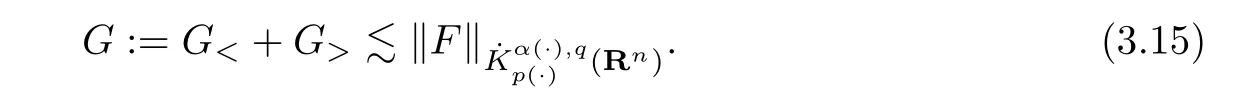
Consequently,the proof of Theorem 3.1 is completed.

Since the proof of Theorem 3.2 is essentially a repetition of the proof of Theorem 3.1,we omit the details.

[1]Kov´aˇcik O,R´akosn´ık J.On spaces Lp(x)and Wk,p(x).Czech.Math.J.,1991,41:592–618.

[2]Chen Y,Levine S,Rao R.Variable exponent,linear growth functionals in image restoration.SIAM J.Appl.Math.,2006,66:1383–1406.

[3]Diening L,R˙uˇziˇcka M.Calder´on-Zygmund operators on generalized Lebesgue spaces Lp(·)and problems related to fluid dynamics.J.Reine.Angew.Math.,2003,563:197–220.

[4]Harjulehto P,H¨ast¨o P,Lˆe´U V,Nuortio M.Overview of differential equations with nonstandard growth.Nonlinear Anal.,2010,72:4551–4574.

[5]Cruz-uribe D,Fiorenza A.Variable Lebesgue Spaces:Foundations and Harmonic Analysis,Applied and Numerical Harmonic Analysis.Basel:Birkh¨auser,2013.

[6]Almeida A,Drihem D.Maximal,potential and singular type operators on Herz spaces with variable exponents.J.Math.Anal.Appl.,2012,394:781–795.

[7]Izuki M.Boundedness of sublinear operators on Herz spaces with variable exponent and application to wavelet characterization.Anal.Math.,2010,36:33–50.

[8]Lu Y,Zhu Y.Boundedness of multilinear Calder´on-Zygmund singular operators on Morrey-Herz spaces with variable exponents.Acta Math.Sin.(Engl.Ser.),2014,30:1180–1194.

[9]Samko S.Variable exponent Herz spaces.Mediterr.J.Math.,2013,10:2007–2025.

[10]Xu J.Variable Besov and Triebel-Lizorkin spaces.Ann.Acad.Sci.Fenn.Math.,2008,33:511–522.

[11]Yang D,Zhuo C,Yuan W.Triebel-Lizorkin type spaces with variable exponents.Banach J.Math.Anal.,2015,9:146–202.

[12]Yang D,Zhuo C,Yuan W.Besov-type spaces with variable smoothness and integrability.J.Funct.Anal.,2015,269:1840–1898.

[13]Zhang P,Wu J.Commutators of the fractional maximal function on variable exponent Lebesgue spaces.Czech.Math.J.,2014,64:183–197.

[14]Herz C.Lipschitz spaces and Bernstein’s theorem on absolutely convergent Fourier transforms.J.Math.Mech.,1968,18:283–324.

[15]Chen Y,Ding Y.The parabolic Littlewood-Paley operator with Hardy space kernels.Canad.Math.Bull.,2009,52:521–534.

[16]Feichtinger H,Weisz F.Herz spaces and summability of Fourier transforms.Math.Nachr.,2008,281:309–324.

[17]Lu S,Yang D,Hu G.Herz Type Spaces and Their Applications.Beijing:Science Press,2008.

[18]Ragusa M.Homogeneous Herz spaces and regularity results.Nonlinear Anal.,2009,71:1909–1914.

[19]Coifman R,Rochberg R,Weiss G.Factorization theorems for Hardy spaces in several variables.Ann.Math.,1976,103:611–635.

[20]Chiarenza F,Frasca M,Longo P.W2,p-solvability of the Dirichlet problem for nondivergence elliptic equations with VMO coefficients.Trans.Amer.Math.Soc.,1993,334:841–853.

[21]Fazio G Di,Ragusa M.Interior estimates in Morrey spaces for strong solutions to nondivergence form equations with discontinuous coefficients.J.Funct.Anal.,1993,112:241–256.

[22]Cruz-uribe D,SFO,Fiorenza A,Martell J,P´erez C.The boundedness of classical operators on variable Lpspaces.Ann.Acad.Sci.Fenn.Math.,2006,31:239–264.

[23]Izuki M.Boundedness of commutators on Herz spaces with variable exponent.Rend.Circ.Mat.Palermo,2010,59:199–213.

[24]Soria F,Weiss G.A remark on singular integrals and power weights.Indiana Univ.Math.J.,1994,43:187–204.

[25]Izuki M.Vector-valued inequalities on Herz spaces and characterizations of Herz-Sobolev spaces with variable exponent.Glasnik Matematicki,2010,45:475–503.

[26]Lu S,Yang D.The decomposition of the weighted Herz spaces and its application.Sci.China(Ser.A),1995,38:147–158.

[27]Dong B,Xu J.New Herz type Besov and Triebel-Lizorkin spaces with variable exponents.J.Funct.Space Appl.,2012:Article ID 384593,27 pp.

[28]Tao S,Wang L.Littlewood-Paley operators on Morrey spaces with variable exponent.The Scientific World Journal,2014:Article ID 790671,10 pp.

[29]Wang L,Tao S.Parameterized Littlewood-Paley operators and their commutators on Herz spaces with variable exponent.Turkish J.Math.,2016,40:122–145.

[30]Wang L,Tao S.Boundedness of Littlewood-Paley operators and their commutators on Herz-Morrey spaces with variable exponent.J.Inequal.Appl.,2014,Article ID:227(2014).

42B20,42B25

A

1674-5647(2017)04-0363-14

10.13447/j.1674-5647.2017.04.09

date:Sept.12,2016.

The NSF(11471033)of China.

E-mail address:wangliwei@ahpu.edu.cn(Wang L W).