基于EEMD和模糊BP神经网络的滚动轴承故障诊断

张国银 王 雪 王海瑞 郝家骥 宋怡然

(昆明理工大学信息工程与自动化学院)

基于EEMD和模糊BP神经网络的滚动轴承故障诊断

张国银 王 雪 王海瑞 郝家骥 宋怡然

(昆明理工大学信息工程与自动化学院)

针对滚动轴承故障振动信号的非平稳特征，提出一种基于总体经验模态分解(EEMD)和模糊BP神经网络的故障诊断方法。首先对滚动轴承的振动信号采用总体经验模态分解方法进行分解，得到若干个本征模态函数分量(IMF)；然后提取各分量的均方差、峭度和能量，把这些特征参数作为学习集和训练集，将学习集输入到模糊BP神经网络中进行学习；最后把训练集输入到特征参数经过学习训练后的模糊BP神经网络中进行故障类型识别，并与BP神经网络进行比较。实验结果表明：所提方法能有效地应用于滚动轴承故障诊断，而且比BP神经网络具有更高的精确度。

滚动轴承 故障诊断 EEMD 模糊BP神经网络 能量 峭度

目前，在滚动轴承的故障诊断中，主要以研究振动信号中所产生的故障特征进行故障诊断。当轴承中的一个或几个元件发生局部故障时，相接触的部件会因撞击而产生能量集中的周期性脉冲信号，从而激起轴承系统各部件的高频固有振动，产生幅值调制现象，不同的故障会有不同的故障信息特征[1]。一般来说，滚动轴承故障诊断技术分为4个过程：首先对选取的能反映滚动轴承状态信息的信号进行预处理；接着对信号进行特征提取，选取能够反映其故障征兆的特征值；然后根据特征值选取恰当的处理方法对特征值进行分析，从而得出其故障状态诊断与分析；最后按照结果做出相应的决策，及时对设备进行相应的处理。而提取故障特征的有效性决定了能否准确地判断故障类型。因此，判断滚动轴承故障的关键就是准确全面地提取故障特征信号。

文献[2]应用模糊神经网络对轨道电路故障进行诊断，取得了较好的效果，但没有对原始信号进行预处理，原始信号中掺杂了干扰信号，会影响对故障类型的判断。文献[3]应用经验模态分解(EMD)和神经网络进行轮轨故障噪声诊断，但是EMD在分解过程中会产生模态混叠现象，同样会对故障分类的识别产生影响。EMD可用于非线性与非平稳信号处理，可是EMD分解本身存在模态混叠等不足，为了减少模态混叠对实验结果带来的影响，Hang N E和Wu Z H提出利用高斯白噪声的总体经验模态分解(EEMD)方法[4，5]。模糊神经网络的关键是对于模糊规则及其隶属度函数的改进，是基于神经网络的学习能力实现，此方法将模糊控制与神经网络联系在一起，既改进了不足，又融合了它的优点[6]。基于上述研究，笔者将EEMD方法和模糊BP神经网络结合起来，对滚动轴承信号进行分析与故障诊断，首先对采集到的轴承噪声信号进行EEMD分解，计算各IMF分量的均方差值、峭度和能量，并将其各均值作为模糊BP神经网络训练和测试的特征参数输入，对滚动轴承3种不同状况下的故障进行分类识别。

1 EEMD方法

滚动轴承振动信号中的噪声干扰严重影响故障诊断的准确性，为此需要使用消噪方法对信号进行处理以减少噪声干扰。具体的消噪方法包括小波滤噪、EMD分解滤噪等。小波消噪具有多分辨率等优点，但小波参数的选择将直接影响诊断结果，并且不能自适应地进行信号分解。EMD作为新的消噪方法，具有自适应分解信号的能力，但EMD分解存在模态混叠、端点效应等问题。因此Huang N E等提出了EEMD分解方法[4，5]。EEMD的本质是在原有信号中加入高斯白噪声的多次EMD，利用白噪声的频率平均分布的统计特性，自适应地从滚动轴承振动信号中分离出高频调制信号，从而有效抑制模态混叠问题。EEMD方法既克服了小波基函数和阈值的选择，又解决了EMD的模态混叠问题。

EEMD算法分解过程的具体步骤如下：

a. 对分析信号x(t)加入随机高斯白噪声序列(一般白噪声标准差是原始信号标准差的0.1～0.4倍)；

b. 对加入白噪声的信号进行EMD分解，得到K个IMF分量cj(t)(j=1，…，K)和余项r(t)；

c. 计算分解后IMF的均值，把各个IMF的均值作为最终的结果。

将步骤a～b重复N次，每次加入不同的白噪声序列，所得的第i次加入白噪声后的信号xi(t)为：

(1)

式中cij(t)——第i次加入高斯白噪声后分解所得的第j个IMF。

步骤c对原信号经过EEMD分解后所得的第j个IMF分量的最终结果cj(t)为：

(2)

(3)

2 模糊BP神经网络

模糊BP神经网络整合了模糊逻辑系统和神经网络的优点，模糊逻辑系统善于通过表达和抽取知识来处理结构化的知识，但是不具备学习能力；神经网络则善于通过样本学习来处理非结构的知识，但是不能对模糊相似信息进行有效区分。这样的结合方式使模糊BP神经网络不仅具有知识易于理解的优点，还无需建立精确的数学模型，适合处理不确定性和非线性问题[7]。模糊BP神经网络的两个组成部分为前件网络和后件网络，前件网络的作用为匹配模糊规则，后件网络的作用则是产生模糊规则[8]。笔者采用BP算法对各节点的隶属度函数进行优化，具体的网络结构有5层，如图1所示。

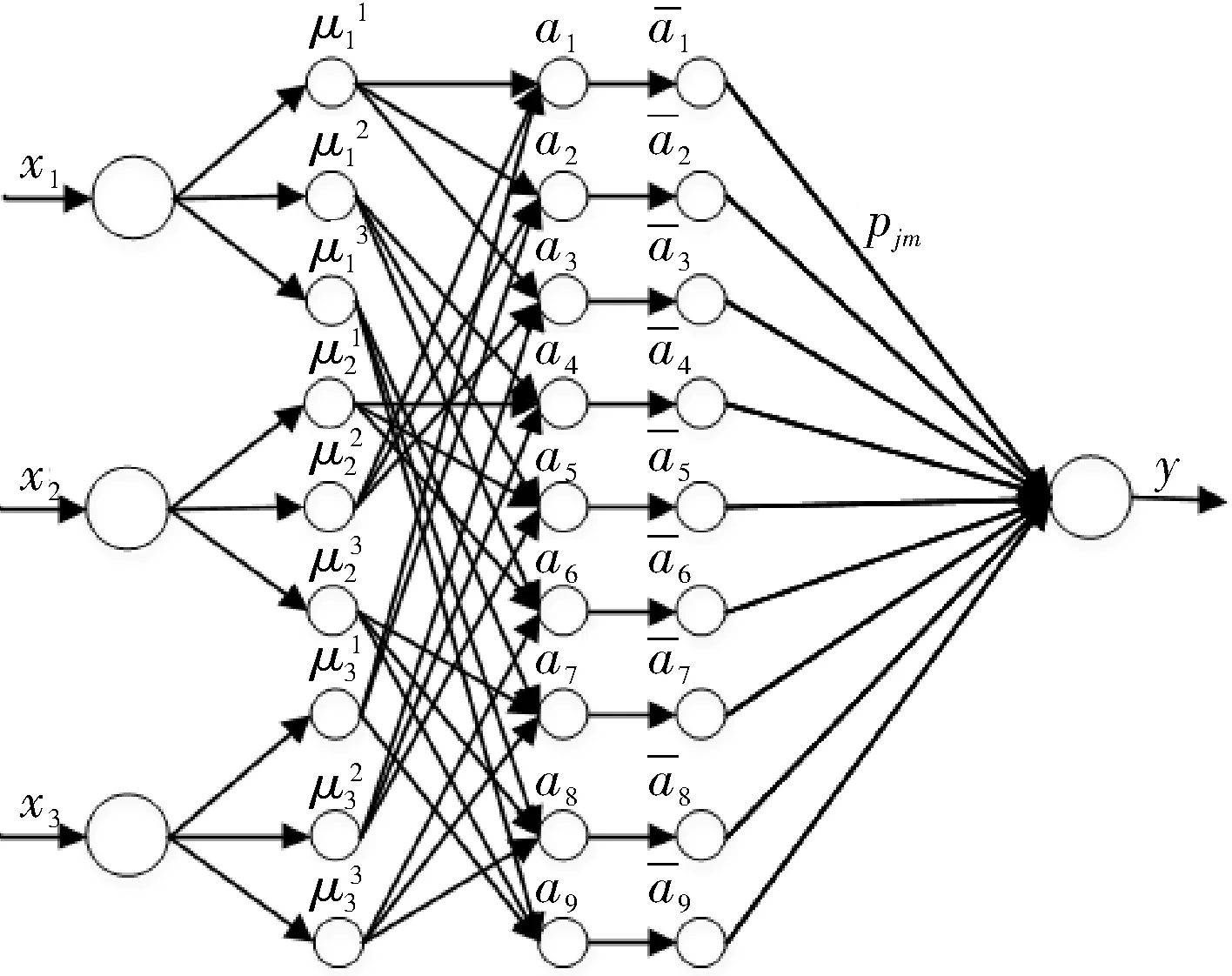
图1 模糊BP神经网络结构

第1层为输入层，有3个神经元(均方差、峭度和能量)作为输入信号(x1,x2,x3)传送到下一层。

3 基于EEMD与模糊BP神经网络的滚动轴承故障诊断方法

峭度值反映了信号中冲击成分的大小[9]，冲击成分所占的比率越大，峭度值越大。由于高频IMF信号中含有故障引起的固有振动成分，因此故障信息最容易提取。当轴承出现不同的故障时，故障信号在各个IMF分量中的能量分布会发生相应的改变，所以可以选择不同频带的能量作为故障识别的特征参量。均方差能反映信号幅值概率密度分布的特性，即幅值分布的离散程度，当滚动轴承出现故障时，由于冲击的增强将导致信号的幅值分布特性发生变化。根据上文所述，可将各IMF分量的均方差值、峭度值和能量值作为模糊BP神经网络的特征参数，能够进行较好的故障分类识别。

通过上述分析，利用EEMD与模糊BP神经网络的滚动轴承故障诊断方法的具体步骤为：

a. 对内圈故障、外圈故障和滚动体故障状态下的信号进行采集；

b. 对每一种状态下的信号进行EEMD分解，得到若干个IMF分量，按其频率大小从高到低依次排列，由于故障信息主要存在于信号的高频部分，故选取前6个IMF分量进行分析；

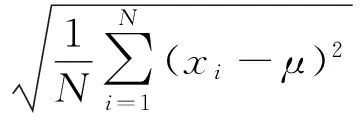
d. 计算每一个信号中分解的6个IMF分量的峭度均值、能量均值和均方差均值，把这些均值作为模糊BP神经网络的参数输入；

e. 将得到的均方差、峭度和能量的均值中的30组数据作为训练样本对模糊BP神经网络进行训练，训练结束后再用其他21组数据作为测试样本进行故障识别。

4 实验结果

为了证明笔者所提方法的可行性，用美国凯斯西储大学振动实验室提供的数据进行实验。实验台包括一个电动机、一个扭矩传感器、一个功率测试计和电子控制器。使用加速度传感器采集轴承的振动加速度信号，分别放置在风扇端轴承座和驱动端的轴承座上。采集此振动信号的采样频率为12kHz。实验中，使用驱动端的加速度数据进行滚动轴承的故障特征提取，进而判断出故障类型。

由于信号中的特征信息主要集中在高频部分，而低频IMF分量所含的特征信息过少，所以保留EEMD分解后的IMF1～IMF6。采用的滚动轴承故障信号包含内圈故障、外圈故障和滚动体故障3种状态。图2为不同状态下的EEMD分解结果。

图2 不同状态下的EEMD分解结果

图3中，模糊BP神经网络在经过225次训练后，误差精度为0.001 0，网络训练结束。图4中，BP神经网络在经过358次训练后，误差精度为0.022 3，无法达到期望的精度，网络训练结束。两者相比，模糊BP神经网络不但在训练次数上比BP神经网络少，而且训练误差也达到了期望值，训练精度也有所提高。

图3 模糊BP神经网络训练误差变化曲线

图4 BP神经网络训练误差变化曲线

用训练好的模糊BP神经网络和BP神经网络分别对测试样本进行分类识别，每种情况各7个测试样本，一共21组数据，见表1。

为了更好地证明笔者所提方法的可行性，表2中列出了两种方法的实际输出结果，并与期望输出结果和故障类型进行对比，BP神经网络的输出设定为3个值，分别代表3个故障，值最大的一个就对应相应的故障。表2中BP神经网络的输出样本“1”代表滚动轴承的内圈故障，“2”代表滚动轴承的外圈故障，“3”代表滚动轴承处于滚动体故障状态。同时，为了更加直观地判断两种方法的优劣，在表3中列出了两种方法的故障识别率对比。

表1 测试数据

表2 模糊BP神经网络与BP神经网络诊断结果

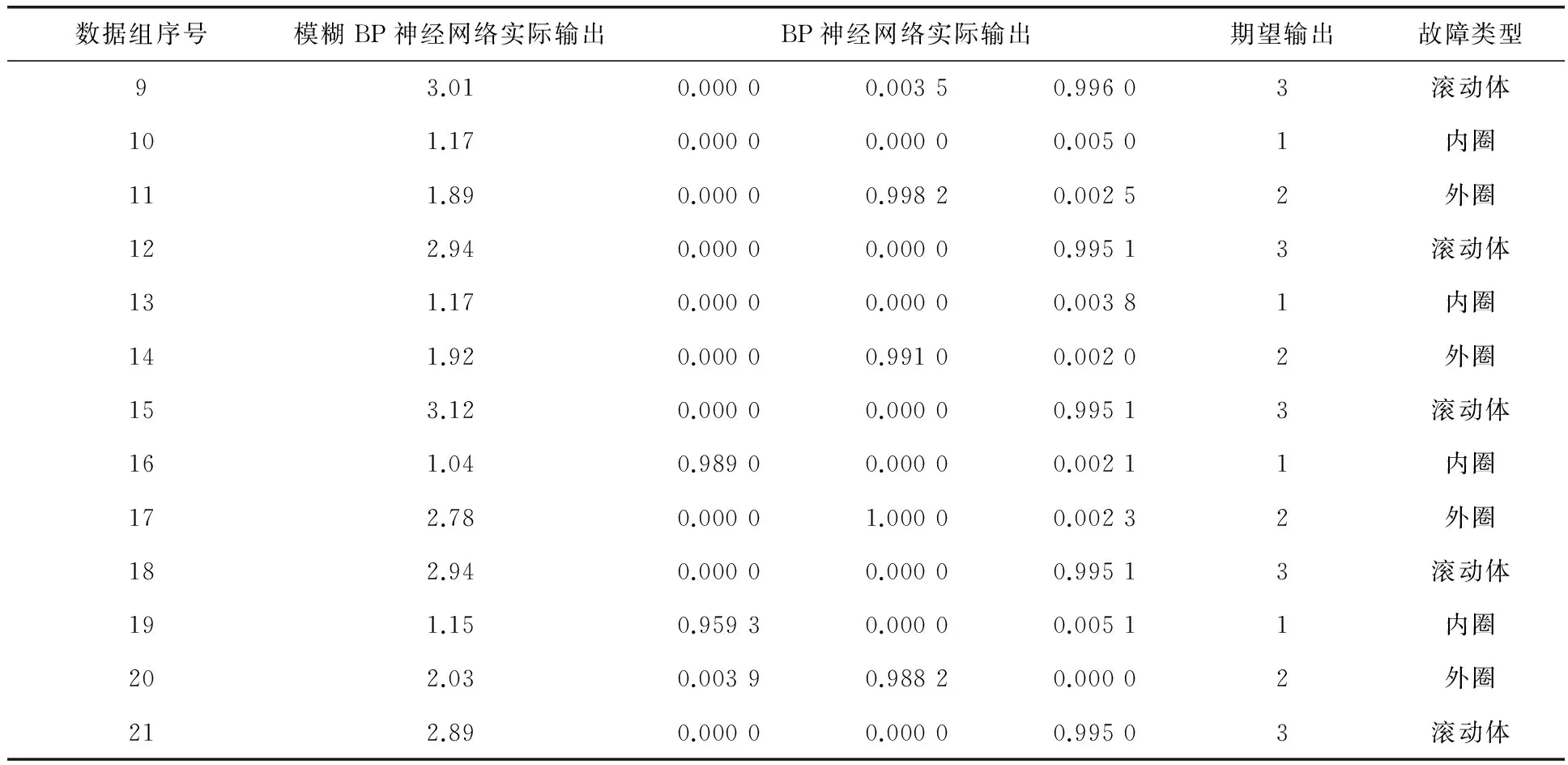
(续表2)

表3 模糊BP神经网络与BP神经网络故障识别率对比

表2中，故障信号经过EEMD分解后再使用上述两种方法都可以根据故障信号中的信息进行故障类型的识别，根据对比结果可知：模糊BP神经网络比BP神经网络具有更高的故障识别率(表3)。在此次实验过程中，模糊BP神经网络出现了一个识别错误，准确率达到95.2%；但BP神经网络中出现了3个识别错误，准确率只有85.7%。而且BP神经网络的错误故障识别都是出现在内圈故障中，这是因为BP神经网络不能处理和描述模糊信息，当数据过于接近时就无法正确区分数据而导致产生错误的结果；而模糊BP神经网络不但具有模糊处理能力，还具有学习能力，弥补了BP神经网络的不足。

5 结束语

针对滚动轴承的故障分析，笔者提出一种将EEMD和模糊BP神经网络结合的方法，实验结果表明该方法不仅对噪声产生了一定的抑制效果，还可以实现多种故障的分类，达到了较好的精度，表明该方法可以有效地区分滚动轴承故障的类别。但是在此次实验中，模糊BP神经网络仍然出现了识别错误，这是因为模糊BP神经网络的模糊规则具有冗余和不精简性，当输入参数和对应的模糊子集较多时，神经网络结构将会变得比较复杂，影响计算效率。因此，改进模糊BP神经网络的结构和参数将是下一步研究的重点。

[1] 胡爱军,马万里,唐贵基.基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J].中国电机工程学报,2012,32(11):106～111.

[2] 黄赞武,魏雪业,刘泽.基于模糊神经网络的轨道电路故障诊断方法研究[J].铁道学报,2012,34(11):54～59.

[3] 江航,尚春阳,高瑞鹏.基于EMD和神经网络的轮轨故障噪声诊断识别方法研究[J].振动与冲击,2014,33(17):34～38.

[4] Huang N E,Shen Z,Long S R,et al.The Empirical Mode of Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J].Proc Royal Society,1988,454:903～905.

[5] Wu Z H,Huang N E.Ensemble Empirical Mode Decomposition:A Noise-Assisted Data Analysis Method[J].Advances in Adaptive Data Analysis,2009,1(1):1～4.

[6] 彭广平,李泳鲜.模糊神经网络在汽车发动机电子点火系统故障诊断中的应用[J].汽车科技,2011,(3):47～50.

[7] 李恒嵬.模糊神经网络研究现状综述[J].辽宁科技学院学报,2010,12(2):15～17.

[8] 周润景.基于MATLAB与fuzzyTECH的模糊与神经网络设计[M].北京:电子工业出版社,2010:197～199.

[9] 吴小涛,杨锰,袁晓辉,等.基于峭度准则EEMD及改进形态滤波方法的轴承故障诊断[J].振动与冲击,2015,34(2):38～44.

RollingBearingFaultDiagnosisBasedonEEMDandFuzzyBPNeuralNetwork

ZHANG Guo-yin, WANG Xue, WANG Hai-rui, HAO Jia-ji, SONG Yi-ran

(FacultyofInformationEngineeringandAutomation,KunmingUniversityofScienceandTechnology)

Considering non-stationary characteristics of bearing’s fault vibration signals, an EEMD and fuzzy neural network-based fault diagnosis method was proposed, in which, having EEMD method adopted to decompose the bearing’s bearing vibration signals into several intrinsic mode function components(IMF); and then, extracting each component’s mean square error, kurtosis and energy and taking them as learning set and training set; and finally, having the learning set input into the fuzzy BP neural network for learning and the training set into the fuzzy BP neural network for fault type identification. Experimental results show that, the method proposed can be effectively applied to the rolling bearing’s fault diagnosis and it outperforms the BP neural network in the accuracy.

rolling bearing, fault diagnosis, EEMD, fuzzy BP neural network, energy, kurtosis

TH133.33

A

1000-3932(2017)01-0034-06

国家自然科学基金项目(61263023)。

张国银(1979-)，副教授，从事计算机应用和智能算法方面的研究。

联 系 人：王雪(1990-)，硕士研究生，从事模式识别和自动化技术方面的研究，1067834094@qq.com。

2016-03-23，

2016-10-10)