合理表示“等可能事件”的所有结果

潘 霞

合理表示“等可能事件”的所有结果

潘 霞

概率是研究不确定现象的数学模型.同学们通过对“等可能条件下的概率”的学习，得到了等可能条件下的概率的计算公式：

一般地，如果一个试验有n个等可能的结果，当其中的m个结果之一出现时，事件A发生，那么事件A发生的概率P（A）可以表示为：

该公式的应用仅限于试验的所有可能出现的结果是有限的，且是等可能的.那么列出试验的所有等可能出现的结果成为解决问题的关键.

一、方法多样

例1（苏科版《数学》教材九年级上册第133页“思考与探索”）抛掷一枚质地均匀的硬币2次，2次抛掷的结果都是正面朝上的概率是多少？

【分析】可以用直接分类列举的方法，也就是我们熟悉的枚举法列出所有等可能出现的结果.

【方法一】列举出所有等可能出现的结果：（正，正），（正，反），（反，正），（反，反），再利用等可能条件下的概率计算公式求其概率.

【分析】为了避免在直接列举的过程中重复或遗漏，可借助表格或树状图列出抛掷一枚质地均匀的硬币2次所有可能出现的结果.

【方法二】表格：

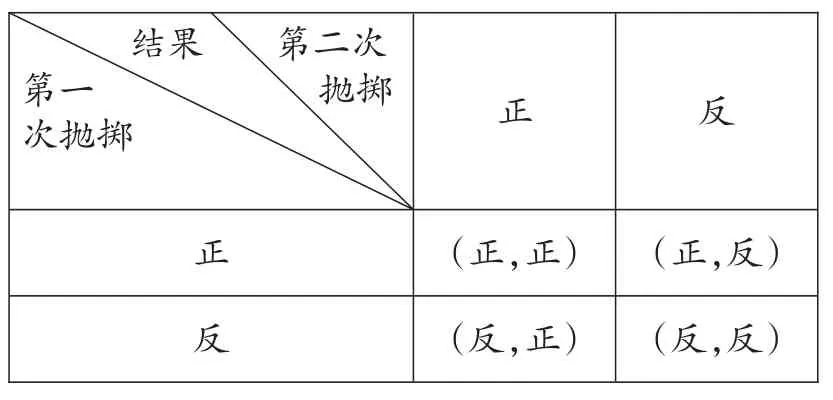
共有4种可能出现的结果，并且它们都是等可能的“.2次抛掷的结果都是正面朝上”记为事件A，它的发生只有一种可能，所以事件A发生的概率P（A）=，即2次抛掷的结果都是正面朝上的概率是

【方法三】树状图：

（同表格求解）

【点评】等可能出现的结果是有限的且易于分类，这种等可能条件下的概率问题，我们都可以借助表格、树状图将所有结果无重复无遗漏地表示出来，并且具有直观性，实际上这两种方法是枚举法的升级版.

这两种方法哪种更合理，更有效？它们各有怎样的特点？在使用的时候又需要注意什么问题？

二、方法优化

在例1中，试验分为2步，并且所有等可能出现的结果数较少，运用表格和树状图求解都比较有效.

例2 若将例1问题中的试验工具硬币改为骰子，两次抛掷骰子点数和为5的概率是多少？

【分析】与抛掷硬币相同，都属于等可能条件下的概率问题，那么我们是选择表格还是树状图来表示所有等可能出现的结果呢？若选择树状图，第一次有六种结果，第二次也有六种结果，也就是共有36种结果数，这是棵枝繁叶茂的树，显然用树状图表示，结果不够清晰.表格就不同了，同学们可以动笔试试哦！

【点评】当试验分2步，但所有等可能出现的结果数较多时，运用表格分析则显得较为清晰、便捷.

例3 抛掷一枚质地均匀的硬币3次，3次抛掷的结果都是正面朝上的概率是多少？

【分析】若用表格求解，得到一个三维的立体表格，而这在二维平面上表示出来是比较困难的，又或者列两个表格，也较为烦琐.

【点评】当试验分为3步时，则一般运用“树状图”列出所有等可能出现的结果.

“有放回无放回试验”在用表格和树状图表示结果数时要注意什么？同学们你们清楚吗？

三、灵活运用

例4 一个不透明的袋子中有大小、质地完全相同的4只小球，小球上分别标有1、2、3、4四个数字.

（1）从袋中随机摸出一只小球，求小球上所标数字为奇数的概率；

（2）从袋中随机摸出一只小球，再从剩下的小球中随机摸出一只小球，求两次摸出的小球上所标数字之和为5的概率.

【分析】第（2）问说明试验有2步，第1步是从4只小球中随机摸1只，而第2步是从剩下的小球，也就是3只小球中随机摸1只，是“无放回的摸球游戏”.所以在解答时要谨慎对待.

解：方法一（列表法）：

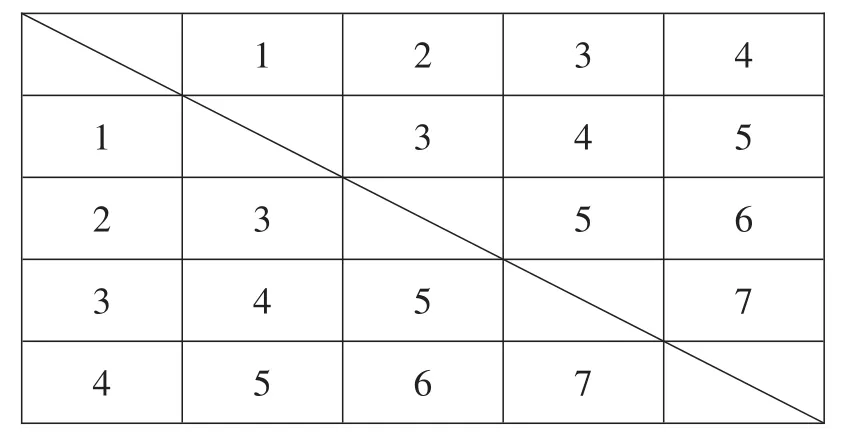
共有12种等可能的结果，其中两次摸出的小球上所标数字之和为5的可能性有4种，所以P（两次摸出的小球数字之和为5）

方法二（树状图）：

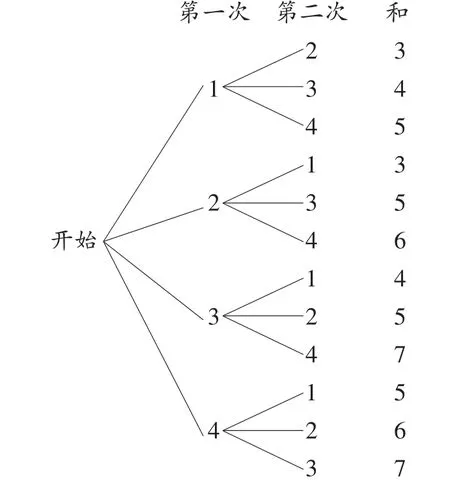
共有12种等可能的结果，其中两次摸出的小球上所标数字之和为5的可能性有4种，所以P（两次摸出的小球数字之和为5）

不管用哪种方法表示试验结果数，它们只是解决问题的工具.哪种方法更合理，需要抓住问题的本质去判断.当然这些解决概率问题的方法只是九牛一毛，随着学习的深入，概率将作为一门独立的学科，等待我们去探究，去发现.

（作者单位：江苏省常州市金坛区白塔中学）