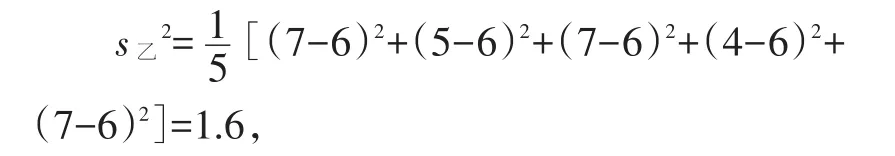方差生活秀

王克美

方差生活秀

王克美

数学源于数学，生活中处处有数学.本文通过生活中的一道中考题的解析与变式，探究平均数与方差解决实际问题的思路与策略，以帮助同学们找寻和感悟通过建立数学模型解决此类问题的一般思路与方法.

一、从生活中来

为了选拔一名同学参加某市中学生射击竞赛，某校对甲、乙两名同学的射击水平进行了测试，结果如下：

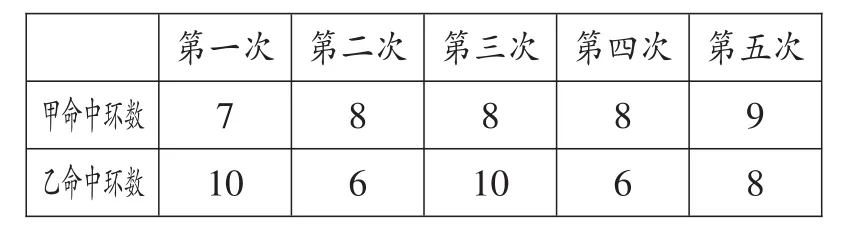
现要挑选一名射击手参加比赛，若你是教练，你认为挑选哪一位比较适宜？为什么？

【解析】我们先来算一算甲和乙命中环数的平均数吧：

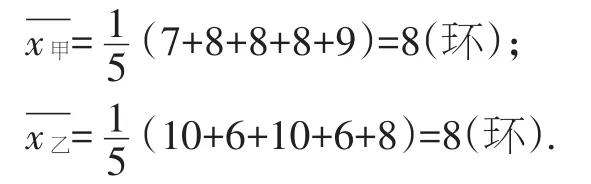
平均数一样，那怎么比较两人成绩的好坏呢？我们来画折线图直观地比较一下.

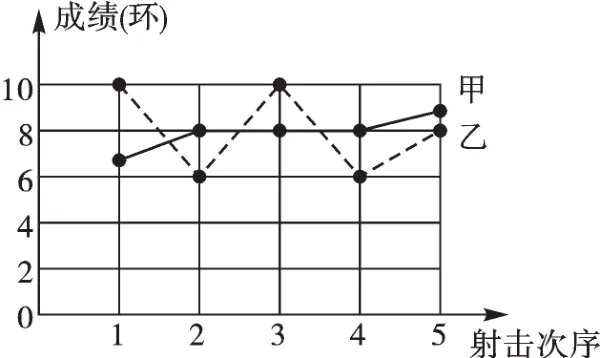
甲、乙两人的平均成绩相同，但是甲每次的射击成绩都接近平均数8，而乙每次的射击成绩偏离平均数较大.在评价数据的稳定性中，我们通常将各数据偏离平均数的波动程度作为指标.

直接计算射击成绩与平均成绩偏差的和，发现它们是一样的.

甲射击成绩与平均成绩的偏差的和（7-8）+（8-8）+（8-8）+（8-8）+（9-8）=0.

乙射击成绩与平均成绩的偏差的和（10-8）+（6-8）+（10-8）+（6-8）+（8-8）=0.

现在我们再计算一下甲、乙两人每次射击成绩与平均成绩的偏差的平方和.

甲：（7-8）2+（8-8）2+（8-8）2+（8-8）2+（9-8）2=2.

乙：（10-8）2+（6-8）2+（10-8）2+（6-8）2+（8-8）2=16.

你发现了甲、乙的区别了吗？

上述各偏差的平方和的大小还与什么有关？

——与射击次数有关！

可用各偏差平方和的平均数来衡量数据的稳定性，一般地，各数据与它们的平均数的差的平方的平均数叫做这组数据的方差，公式为：

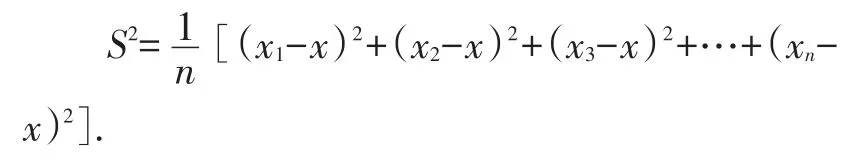
特别地：如果方差与标准差为零，说明数据都没有偏差，即每个数都一样.

二、到生活中去

王大伯几年前承办了甲、乙两片荒山，各栽100棵杨梅树，成活98%，现已挂果，经济效益初步显现，为了分析收成情况，他分别从两山上随意各采摘了4棵树上的杨梅，每棵的产量如折线统计图所示.

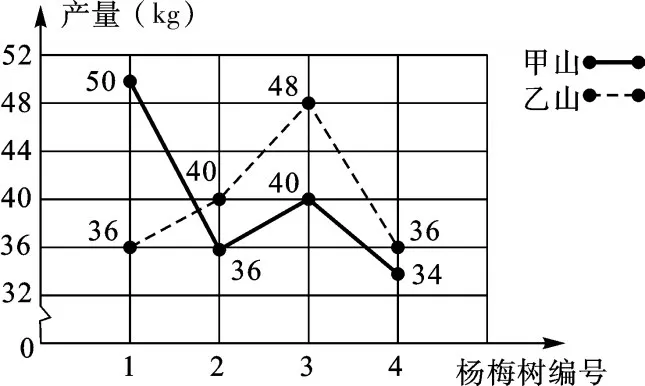
（1）分别计算甲、乙两山样本的平均数，并估算出甲乙两山杨梅的产量总和；

（2）试通过计算说明，哪个山上的杨梅产量较稳定？

【解析】（1）因为甲、乙两山的样本的平均数相等，都为40kg，又由甲、乙两山各栽100棵杨梅树，成活率为98%，进而得出甲、乙两山杨梅的产量总和约为2×100×98%×40=7840（kg）；

（2）对标准差的值进行比较，得出乙山的杨梅产量较稳定.

三、在生活中深化

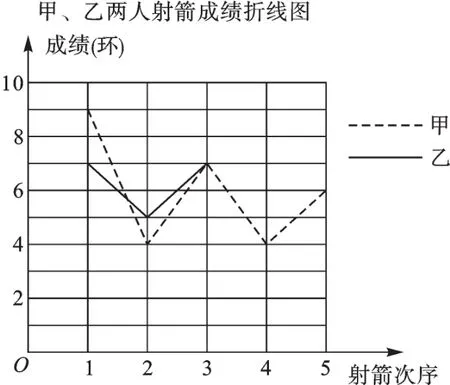
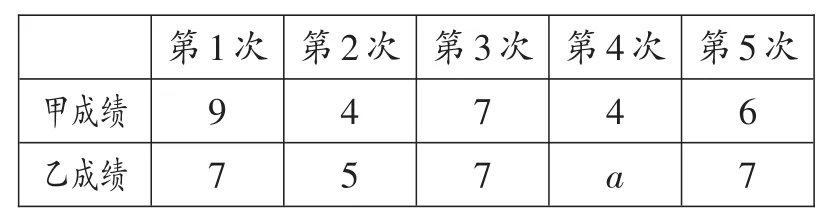
某社区准备在甲、乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，他们的总成绩（单位：环）相同，小宇根据他们的成绩绘制了如下尚不完整的统计图表，并计算了甲成绩的平均数和方差（见小宇的作业）.

甲、乙两人射箭成绩统计表

（1）a=___，x乙=___；

（2）请完成图中表示乙成绩变化情况的折线；

（3）①观察图，可看出___的成绩比较稳定（填“甲”或“乙”）.参照小宇的计算方法，计算乙成绩的方差，并验证你的判断.

②请你从平均数和方差的角度分析，谁将被选中.

【解析】（1）由题意得：甲的总成绩是：9+4+7+4+6=30，

则a=30-7-5-7-7=4，x乙=30÷5=6，

故答案为：4，6.

（2）根据（1）中所求得出a的值进而得出折线图如图所示：

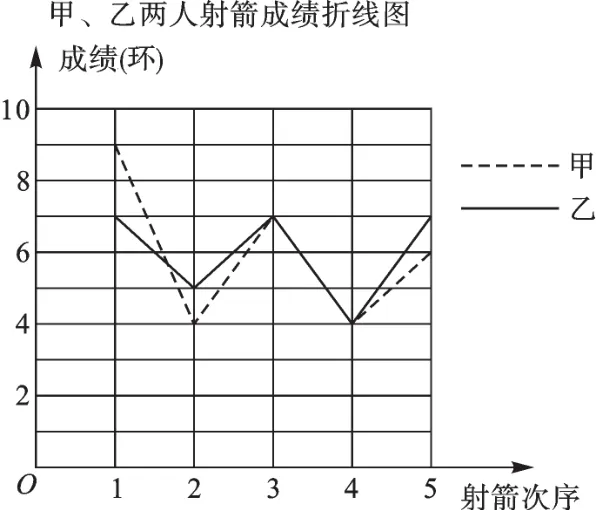
②因为两人成绩的平均水平（平均数）相同，根据方差得出乙的成绩比甲稳定，所以乙将被选中.

（作者单位：江苏省宿迁市泗洪县第一实验学校）

（3）①观察图，可看出乙的成绩比较稳定，故答案为：乙；