灌溉输配水系统明满流的全隐式耦合模拟及验证

刘锦涛，章少辉，许 迪，白美健，刘群昌



灌溉输配水系统明满流的全隐式耦合模拟及验证

刘锦涛1,2，章少辉1※，许 迪1，白美健1，刘群昌1

（1. 中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100038； 2. 中国农业大学水利与土木工程学院，北京100083）

准确合理地模拟具有自由表面的渠/管道明流和具有压力的管道满流运动过程，是设计、评价和管理灌区输配水系统的基础。为此，该文基于Preissmann窄缝法的概念，采用Saint-Venant方程组描述灌溉输配水系统的明满流过程，在交错空间离散单元格上，建立了基于全隐式标量耗散有限体积法的明满流耦合模拟模型。借助标准的室内物理模型观测数据和石家庄冶河灌区山尹村试验站野外原型观测数据，对模型的模拟效果进行了验证。结果表明，与基于显式向量耗散有限体积法建立的模型相比，该文建立的明满流耦合模拟模型具有类似的模拟精度，但水量平衡误差在室内和野外试验条件下仅为前者的13%和1.2%，且计算效率提高了约5.2倍；与基于四点偏心有限差分法建立的模型相比，模拟精度显著提高，水量平衡误差在室内和野外试验条件下仅为前者的7.6%和0.6%，且效率提高了1.3倍，故该文建立的模型有效克服了已有模型无法统一模拟精度和效率的缺陷，更适于实际工程问题，为灌区输配水系统的设计优化和管理评价提供了数值模拟方法。

灌溉；输水系统; 有限差分法；明满流；全隐式；耦合；模拟

0 前 言

灌溉输配水系统由渠道和管道构成，准确合理地模拟该系统中的水流运动过程，是设计、评价和管理灌区输配水过程的基础[1-4]。在该系统中，渠道水流呈现出具有自由表面的无压流，管道水流则同时呈现出具有自由表面的无压流和满管的有压流，这种有压-无压交替变化的明满流运动过程[5-7]，导致数值模拟困难，是输配水系统水动力学模拟的难题[8-18]。

为了采用Saint-Venant方程组统一地描述输配水系统中的明满流过程，Preissmann提出了窄缝法（称之为Preissmann窄缝法）[5-6]。在此基础上，构建了四点偏心有限差分法，在输配水系统的明满流过程模拟中获得了极为广泛的应用[18-24]。然而，无压流中的重力扩散波和有压流中的管道弹性波传播速度巨大的差异，导致2种不同流态的稳定性条件对时间步长限制的显著不同，致使明满流的耦合模拟过程复杂且效率较低[5,13]。另外四点偏心有限差分法的质量守恒性较差[25]，而基于差分和插值概念的特征线法，在明满流耦合模拟过程中表现出了类似的缺陷[13]。为此，学者们把在地表浅水流模拟中已被广泛应用的显式向量耗散有限体积法推广至明满流的耦合模拟中[13]，表现出了极高的精度，但其显式和向量耗散特征导致效率极低[25-28]，成为阻碍其推广至工程实际应用的主要障碍。

本文基于Preissmann窄缝法原理，采用Saint-Venant方程组描述灌溉输配水系统的明满流过程，在交错空间离散单元格上，建立基于全隐式标量耗散有限体积法的明满流耦合模拟模型，以克服四点偏心有限差分法精度较低和显式向量耗散有限体积法效率低的缺陷，达到明满流耦合模拟同时具备高精度和高效率的目的。借助标准的室内物理模型观测数据和石家庄冶河灌区山尹村试验站野外原型观测数据，通过与显式向量耗散有限体积法及四点偏心有限差分法的模拟结果进行对比，验证基于全隐式标量耗散有限体积法的明满流耦合模拟模型的模拟效果。

1 控制方程

渠道中的水流是具有自由表面的无压流，常采用Saint-Venant方程组描述[5]。管道中的水流则呈现出无压流和满管的有压流交替变化的状态，而有压流需考虑管材及水流的可压缩性[6]。为此，Preissmann提出了窄缝法（简称Preissmann窄缝法）[7]，以统一描述无压和有压流（图1）。

注：B是管道顶端水面宽度，m。下同。

由图1可直观地看出，Preissmann窄缝法把有压和无压流看作一种具有特殊横断面的渠道水流运动过程。故可采用守恒型Saint-Venant方程组统一地描述明满流运动过程，包括质量守恒方程式（1）和动量守恒方程式（2）[7]：

式中为时间坐标，s；为空间坐标，m；为过流断面面积，m2；为通过任意断面的过流量，m3/s；为通过任意断面的流速，m/s；=z+为渠/管道内的水位（自由水位或测压管水头）相对高程，且z为渠/管底相对高程，为渠/管内的水深，m；为重力加速度，m/s2；为水力半径，m；为曼宁糙率系数，s/m1/3。

如图1所示，管道水流处于满管状态时，假设管道上端存在一个极窄的水面宽度，以此模拟有压流动。为模拟不同管径与管材下的有压流，图1b中的按下式计算：

式中为管道弹性波速，m/s。

2 渠/管道横断面几何参数

数值求解式（1）和式（2）之前，需首先给定渠/管道的横断面几何参数。由于本文的验证部分仅涉及矩形和圆形断面，故仅给出这2种横断面几何参数，其他诸如U型和梯形等横断面几何参数，可在相关著作中找到[29]。

2.1 矩形横断面

图2给出了矩形横断面示意图及其参数表达。依据该图，可获得过流断面面积、湿周和之间的关系式表达如下：

式中为湿周，m。

注：h为管道水深，m。下同。

2.2 圆形横断面

图3给出了圆形断面的几何参数，依据该图，可直接把、和之间的关系表达为[30]：

当<时，

当<2时，

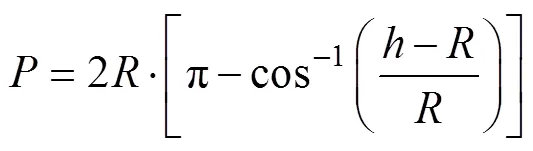
基于上述矩形和圆形各水力关系式，可直接依据公式=/计算出水力半径。

注：R为管道半径m；a为水面线相对于管道横断面圆心的夹角，(°)。

3 数值解法

在空间离散单元格中心处，定义过流断面面积和与其相关的变量（、、）；在空间离散单元格边界上，定义流量和流速，此即交错空间离散单元格的概念。若涉及任意空间离散单元格中心处的流速，按照(u-1/2+u+1/2)/2计算，若涉及任意空间离散单元格边界（+1/2）上的过流断面面积A+1/2，则按照(A+A+1)/2计算，其他变量的获取方式以此类推。

基于此，在空间离散单元格及其边界上，采用标量耗散有限体积法分别对式（1）和式（2）各项进行空间离散，并利用全隐时间格式对控制方程式（1）和式（2）的空间离散表达式进行时间离散，在实现无条件稳定数值求解的基础上，达到对输配水系统中有压和无压流（明满流）过程耦合模拟的目的。

3.1 空间离散

借助流量与过流断面面积之间的关系式=×，基于有限体积法的基本概念，在任意空间单元格和单元格边界（+1/2）上，分别对式（1）和式（2）进行空间积分平均如下[25]：

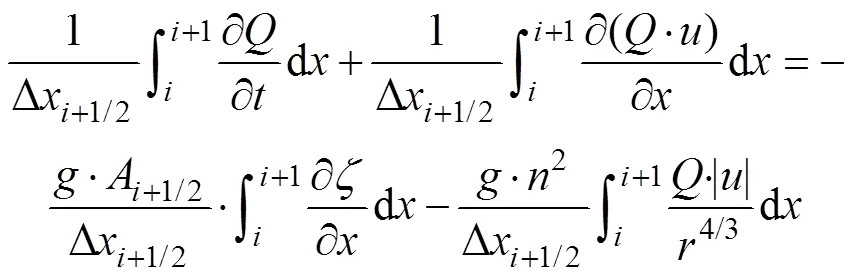
式中Dx=x+1/2-x-1/2，m；Dx+1/2=x+1-x，m。

式（15）中的第1项被空间离散如下：

式（15）中的第2项被空间离散如下：

采用标量耗散有限体积法对式（18）中的(×)+1/2进行空间离散如下：

式中c+1/2=(×A+1/2/B+1/2)1/2是单元格边界处非满管无压流的重力波速或满管有压流的管道弹性波速，m/s；Fr+1/2=u+1/2/c+1/2是单元格边界(+1/2)处的傅汝德数。

式（19）中的c+1/2和Fr+1/2被定义如下[31]：

式中和+1是傅汝德数分裂函数，被定义如下：

通过把式（19）中的下标(+1/2)变换成(-1/2)，可获得(×)-1/2的空间离散表达式。把这2个表达式及式（17）代入式（15），经过合并同类项后，即可获得质量守恒方程式（1）的空间离散式：

式中、和分别是与单元格(+1)、和(-1)相关的系数，分别表达如下：

式（17）中的第1项被空间离散如下：

式（17）中的第2项被空间离散如下：

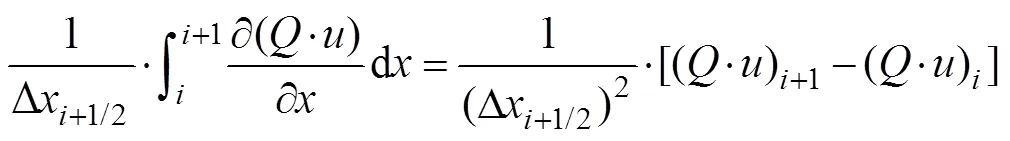
采用标量耗散有限体积法对式（29）中的(×)+1进行空间离散如下：

通过比较式（30）与式（19）可以看出，两者的离散方式在形式上完全相同，差异仅在变量（和）及下标。故通过变化式（20）~式（23）的下标，即可获得式（30）中c+1和Fr+1的定义式。同理可获得式（29）中(×)-1的空间离散式。

式（16）中的第3项被空间离散如下：

式中A是由初始水深假设（详见“稳定性条件和初始及边界条件”）计算获得初始过流断面。

式（16）中的第4项被空间离散如下，

通过把以上各空间离散式代入式（16），即可获得动量守恒方程式（2）的空间离散式如下：

式中+1/2、+1/2、+1/2和+1/2分别是与单元格边界(+3/2)、(+1/2)和(-1/2)相关的系数，分别表达如下：

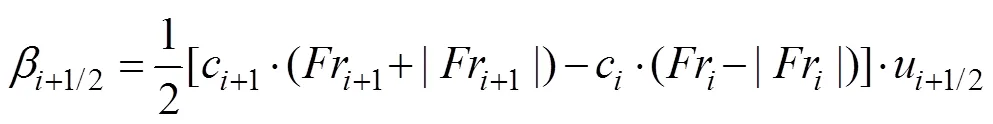
3.2 时间离散

采用全隐时间格式，对质量守恒方程和动量守恒方程的空间离散式（25）及式（34）分别离散如下：

式中n为真实时间迭代步；D为真实时间离散步长，s。

Saint-Venant方程组的双曲型数学属性，使其时空离散式（38）和式（39）难以无条件收敛[31]，为此，采用双时间步法对这2个时空离散式进行处理如下[32-33]：

式中为虚拟时间迭代步；D为虚拟时间离散步长，s。

从式（40）和式（41）可以看出，若虚拟时间迭代步收敛，这2个表达式左侧第1项都将趋于0，式（40）和式（41）即是标准的皮卡迭代式。然而恰恰是这2个虚拟时间项，使得式（40）和式（41）能以绝对收敛的形式达到无条件稳定模拟的目的，这是皮卡迭代方法不具备的优点。为明确这一点，通过对式（40）和式（41）进行合并同类项处理后，获得如下2个待解式：

式中和+1/2分别是与单元格及其边界（+1/2）相关的时空步长比值，=D/Dx，+1/2=D/Dx+1/2；是真实时间步长和虚拟时间步长的比值D/Dt。

3.3 数值求解

通过动态判断渠/管道内的水流态并设置适当的Dt，获得适宜的值，可使式（42）和式（43）始终保持对角占优而达到绝对快速收敛，从而获得无条件稳定性模拟的目的，这即是皮卡迭代方法不具备的功能。由于式（42）和式（43）的系数矩阵在数值模拟中能始终保持对角占优，故采用高斯-赛德尔迭代法[34]，即可高效解算该方程组，其收敛条件如下：

式中是预先设定的误差值，下文取值10-5。

3.4 稳定条件和初始与边界条件

待解式（42）和式（43）形成的代数方程组的系数矩阵能始终保持对角占优[11]，故该方程组的求解过程可实现无条件稳定收敛，这意味着时间离散步长D可依据实际物理问题而取任意值。

渠/管道内初始无水的零水深，是Saint-Venant方程组的奇点，故需假设初始水深值0=10-10m[31]。边界条件包括入流、出流和无流3种条件，而空间交错单元格的另一个优点是[35]，仅需对质量守恒方程时空离散式（42）在边界处给定流量（入流量、出流量和零流量）条件，而无需再对动量守恒方程时空离散式（43）设置边界条件。这可有效保证渠/管道有压与无压流耦合模拟过程中的水量平衡性，提高模拟精度。

4 模拟验证

采用室内物理模型试验和野外原型观测试验数据，并选取基于显式向量耗散有限体积法和四点偏心有限差分法建立的明满流耦合模拟模型作为对比模型，对上述建立的模型进行模拟效果对比验证。在下文验证过程中，水量平衡误差计算如下[31]：

式中in、out和domain分别是在模拟时段内流入、流出和驻留在渠/管道内的水量，m3。

4.1 室内物理模型观测试验验证

本实例是一个国际标准算例[13]，试验装置见图4。该试验装置的主体管道是一长度为10 m的封闭管道，横断面为矩形，高度为0.148 m，宽为0.51 m。曼宁糙率= 0.012 s/m1/3。初始流量为0= 0，初始水头为0= 0.128 m。图5是实测获得的上下游边界处水深随时间的变化过程。在距离上游闸门3.5 m处设置测点，用于观测该点的水深-压力变化过程。

图4 室内物理模型试验装置示意图

图5 室内物理模型试验上下游水深演变过程实测值

在数值模拟过程中，3种解法（本文解法、显式向量耗散有限体积法和四点偏心有限差分法）的空间离散步长均取0.01 m，全隐式标量耗散有限体积法的时间步长取0.01 s（由于该解法无条件稳定，即没有稳定性条件限制，故还可取其他值，但必须能分辨出满管条件下水击波动的运动过程），显式向量耗散有限体积法和四点偏心有限差分法的时间步长，则需满足CFL稳定性条件（以Courant、Friedrichs和Lewy 3人的名字命名的时间格式稳定性必要条件[25]），即CFL数小于1（明满流条件下满足该稳定性的时间步长值远小于0.01 s）。另外，全隐式标量耗散有限体积法和显式向量耗散有限体积法的管道弹性波速取值60 m/s[13]，四点偏心有限差分法的管道弹性波速取值10 m/s[13]。

依据参数及初始与边界条件，图6给出了模拟值与实测值之间的对比。可以直观地看出，基于全隐式标量耗散有限体积法和显式向量耗散有限体积法建立的模型的模拟结果，均与实测数据之间具有良好的拟合度，两者的水量平衡误差分别为0.16%和1.2%，所耗用的计算时间分别为3.2和19.8 s（CPU i7-6700，WIN7），全隐式标量耗散有限体积法的水量平衡误差仅为显式向量耗散有限体积法的13%，计算效率提高了约5.2倍。四点偏心有限差分法的水量平衡误差为2.1%，隐式标量耗散有限体积法水量平衡误差值在野外试验条件下仅为四点偏心有限差分法的7.6%。四点偏心有限差分法模拟结果与实测值之间的差异则较大，这与该解法无法再取更大的管道弹性波速值（否则模拟结果即失稳）密切相关[15]。与此同时，四点偏心有限差分法的计算耗时为7.4 s，本文提出的模型的计算效率比之提高了1.3倍。故在室内物理模型条件下，本文建立的模型达到了同时提高模拟精度和效率的目的。

4.2 野外原型观测试验验证

该算例位于河北省石家庄冶河灌区山尹村试验站。观测试验于2013年4月5日进行。观测渠/管段长为混凝土材质，水平向长度为1018 m，垂向剖面参数见图7。其中矩形断面为方形，宽和高都为1 m，圆形断面的直径为1 m。在距离下游200 m的位置处，设置观测点，用于观测该点处的水深/水压变化过程。从上游开始进水计时，上游入流量为0.08 m3/s。在计时开始后的30 min时打开下游阀门，40 min时关闭下游阀门，打开和关闭阀门的时间为13和15 s，按照线性方式打开和关闭阀门。

注：e为水量平衡误差。下同。

图7 野外原型试验装置示意图

在数值模拟过程中，空间离散步长均取1 m，全隐式标量耗散有限体积法的时间步长取1 s，显式向量耗散有限体积法和四点偏心有限差分法的时间步长，则需满足CFL稳定性条件，即CFL数小于1（该条件下的时间步长值远小于1 s）。另外，全隐式标量耗散有限体积法和标量耗散有限体积法的管道弹性波速取值60 m/s[13]，四点偏心有限差分法的管道弹性波速取值10 m/s[13]。

图8给出了全隐式标量耗散有限体积法、显式向量耗散有限体积法和四点偏心有限差分法的模拟结果与实测值结果之间的对比情况。从中可以看出，全隐式标量耗散有限体积法和显式向量耗散有限体积法的模拟精度显著高于四点偏心有限差分法。四点偏心有限差分法模拟精度较低的原因，是其取的管道弹性波速值较低密切相关，但该解法无法再取更大的管道弹性波速值，否则模拟结果将失稳。另外，全隐式标量耗散有限体积法、显式向量耗散有限体积法和四点偏心有限差分法的水量平衡误差分别为0.016%、1.35%和2.68%，计算耗用时间分别为16.6、103.8和38.2 s（CPU i7-6700，WIN7），即与显式向量耗散有限体积法和四点偏心有限差分法相比，全隐式标量耗散有限体积法的计算效率分别提高了约5.2倍和1.3倍。全隐式标量耗散有限体积法水量平衡误差值在野外试验条件下仅为四点偏心有限差分法的0.6%。这表明，在野外原型观测试验条件下，本文建立的模型达到了同时提高模拟精度和效率的目的。

图8 3种方法模拟实例2的计算结果与实测值之间的比较

5 结 论

本文基于Preissmann窄缝法的概念，采用Saint- Venant方程组描述灌溉输配水系统的明满流过程，在交错空间离散单元格上，构造了该方程组描述明满流时的全隐式标量耗散有限体积法时空离散式，借助高斯-赛德尔迭代法解算该时空离散式，建立了高效和高精度模拟灌溉输配水系统明满流的数值模拟模型。

借助标准的室内物理模型观测数据和石家庄冶河灌区山尹村试验站野外原型观测数据，以基于显式标量耗散有限体积法和四点偏心有限差分法建立的模型作为对比模型，对本文建立的模型的模拟效果进行了验证。结果表明，与基于显式向量耗散有限体积法相比，本文建立的明满流耦合模拟模型具有类似的模拟精度，但在室内和野外试验条件下仅为前者的13%和1.2%，且计算效率提高了约5.2倍；与四点偏心有限差分法相比，模拟精度显著提高，水量平衡误差值在室内和野外试验条件下仅为前者的7.6%和0.6%，故本文建立的模型有效克服了无法统一模拟精度和效率的缺陷，更适于实际工程问题，为灌区输配水系统的设计优化和管理评价提供了数值模拟方法。

[1] González-Cebollada C, Macarulla B, Sallán D. Recursive design of pressurized branched irrigation networks[J]. Journal of Irrigation & Drainage Engineering, 2011, 137(6): 375－382.

[2] Moreno M A, Medina D, Ortega J F, et al. Optimal design of center pivot systems with water supplied from wells[J]. Agricultural Water Management, 2012, 107(10): 112－121.

[3] Estrada C, González C, Aliod R, et al. Improved pressurized pipe network hydraulic solver for applications in irrigation systems.[J]. Journal of Irrigation & Drainage Engineering, 2009, 135(4): 421－430.

[4] 章少辉，刘群昌，白美健，等. 规模化灌溉管网非恒定流模拟研究[J]. 灌溉排水学报，2014，33(z1)：325－330. Zhang Shaohui, Liu Qunchang, Bai Meijian, et al. Unsteady water flow simulation for large scale irrigation network[J]. Journal of Irrigation and Drainage, 2014, 33(z1): 325－330. (in Chinese with English abstract)

[5] 江春波，张永良，丁则平. 计算流体力学[M]. 北京：中国电力出版社，2007.

[6] 杨开林. 长距离输水水力控制的研究进展与前沿科学问题[J]. 水利学报，2016，47(3)：424－435. Yang Kailin. Review and frontier scientific issues of hydraulic control for long distance water diversion[J].Journal of Hydraulic Engineering, 2016, 47(3): 424－435. (in Chinese with English abstract)

[7] Garcia Navarro P, Alcrudo F, Priestley A. An implicit method for water flow modeling in channels and pipes[J]. Journal of Hydraulic Research, 1994, 32(5): 721－742.

[8] Bourdarias C, Gerbi S. A finite volume scheme for a model coupling free surface and pressurised flows in pipes[J]. Journal of Computational & Applied Mathematics, 2007, 209(1): 109－131.

[9] Reca J, García-Manzano A, Martínez J. Optimal pumping scheduling for complex irrigation water distribution systems[J]. Journal of Water Resources Planning & Management, 2014, 140(5): 630－637.

[10] Bourdarias C, Ersoy M, Gerbi S. Unsteady mixed flows in non uniform closed water pipes: A full kinetic approach[J]. Numerische Mathematik, 2014, 128(2): 217－263.

[11] Trajkovic B, Ivetic M, Calomino F, et al. Investigation of transition from free surface to pressurized flow in a circular pipe[J]. Water Science & Technology, 1999, 39(9): 105－112.

[12] Arturo S León, Mohamed S Ghidaoui, Arthur R Schmidt, et al. Application of Godunov-type schemes to transient mixed flows[J]. Journal of Hydraulic Research, 2009, 47(2): 147－156.

[13] Wiggert D C. Transient flow in free-surface pressurized systems[J]. Journal of the Hydraulics Division, 1972, 98(1):1 1－27.

[14] Pato J, Garcia-Navarro P. A pipe network simulation model with dynamic transition between free surface and pressurized flow[J]. Procedia Engineering, 2014, 70: 641－650.

[15] Musandji Fuamba. Contribution on transient flow modeling in storm sewers[J]. Journal of Hydraulic Research, 2002, 40(6): 685－693.

[16] Bourdarias C, Gerbi S. A kinetic scheme for unsteady pressurised flows in closed water pipes[J]. Journal of Computational & Applied Mathematics, 2010, 234(7): 2098－2105.

[17] Henine H, Nédélec Y, Ribstein P. Coupled modelling of the effect of overpressure on water discharge in a tile drainage system[J]. Journal of Hydrology, 2014, 511(7): 39－48.

[18] Kerger F. An exact Riemann solver and a Godunov scheme for simulating highly transient mixed flows.[J]. Journal of Computational & Applied Mathematics, 2011, 235(8): 2030－2040.

[19] 徐文卓. 长距离输水系统明满流及水位调节时的水力控制研究[D]. 天津：天津大学，2007. Xu Wenzhuo. Study on Free-surface-pressurized Flow and Water Level Modulation Hydraulic Control in The Long- distance Water Diversion System[D]. Tianjin: Tianjin University, 2007. (in Chinese with English abstract)

[20] 万五一，练继建，王俊. 明渠-结合池-暗管输水系统水力瞬变过程计算[J]. 水利学报，2003，34(8)：16－20. Wan Wuyi, Lian Jijian, Wang Jun. Numerical simulation of hydraulic transients in open channel-surge pool-pressure conduit system[J]. Journal of Hydraulic Engineering, 2003, 34(8): 16－20. (in Chinese with English abstract)

[21] 陈杨，俞国青. 明满流过渡及跨临界流一维数值模拟[J]. 水利水电科技进展，2010，30(1)：80－84.

Chen Yang, Yu Guoqing. One-dimensional numerical simulation of transcritical flows and transition between free surface and pressurized flows[J]. Advances in Science and Technology of Water Resources, 2010, 30(1): 80－84. (in Chinese with English abstract)

[22] 杨开林. 明渠结合有压管调水系统的水力瞬变计算[J]. 水利水电技术，2002，33(4)：5－7. Yang Kailin. Simulation of hydraulic transients in water diversion projects with open channels and pressurized pipelines[J]. Water Resources and Hydropower Engineering, 2002, 33(4): 5－7. (in Chinese with English abstract)

[23] 杨敏，李强，李琳，等. 有压管道充水过程数值模拟[J]. 水利学报，2007，38(2)：171－175. Yang Min, Li Qiang, Li Lin, et al. Numerical simulation of water-filling process in pressure conduit[J].Journal of Hydraulic Engineering, 2007, 38(2): 171－175. (in Chinese with English abstract)

[24] 柳园园，王船海，吴朱昊，等. 城市排水管网明满交替非恒定流数学模型的研究[J]. 水动力学研究与进展，2016，31(2)：210－219. Liu Yuanyuan, Wang Chuanhai, Wu Zhuhao, et al. Study on free-surface-pressurized flow mathematical model for urban drainage networks[J]. Chinese Journal of Hydrodynamics, 2016, 31(2): 210－219. (in Chinese with English abstract)

[25] Leveque R J. Finite volume methods for hyperbolic problems [J]. Meccanica, 2004, 39(1): 88－89.

[26] Rogers B D, Borthwick A G L, Taylor P H. Mathematical balancing of flux gradient and source terms prior to using Roe’s approximate Riemann solver[J]. Journal of Computational Physics, 2003, 192 (2): 422–451.

[27] Murillo J, Burguete J, Brufau P, et al. Coupling between shallow water and solute flow equations: Analysis and management of source terms in 2D[J]. International Journal for Numerical Methods in Fluids, 2005, 49(3): 267－299.

[28] Sanders B F, Begnudelli L. Unstructured grid finite-volume algorithm for shallow-water flow and scalar transport with wetting and drying[J]. Journal of Hydraulic Engineering, 2006, 132(4): 371－384.

[29] 郭元裕. 农田水利学：第3版[M]. 北京：中国水利水电出版社，1997.

[30] Gunduz O, Aral M M. River networks and groundwater flow: A simultaneous solution of a coupled system[J]. Journal of Hydrology, 2005, 301(1): 216－234.

[31] Zhang Shaohui, Xu Di, Bai Meijian, et al. Fully coupled simulation for surface water flow and solute transport in basin fertigation[J]. Journal of Irrigation and Drainage Engineering, 2016, 142(12): 04016062.

[32] Jameson A, Yoon S. Lower-upper implicit schemes with multiple grids for the Euler equations[J]. AIAA Journal, 2015, 25(7): 929－935.

[33] Yu H, Huang G, Wu C. Efficient finite-volume model for shallow-water flows using an implicit dual time-stepping method[J]. Journal of Hydraulic Engineering, 2015, 141(6): 04015004.

[34] Stoer J, Bulirsch R. Introduction to numerical analysis[M]. New York: Springer Science & Business Media, 2013.

[35] Strelkoff T S, Tamimi A H, Clemmens A J. Two-dimensional basin flow with irregular bottom configuration[J]. Journal of Irrigation and Drainage Engineering, 2003, 129(6): 391－401.

刘锦涛，章少辉，许 迪，白美健，刘群昌. 灌溉输配水系统明满流的全隐式耦合模拟及验证[J]. 农业工程学报，2017，33(19)：124－130. doi：10.11975/j.issn.1002-6819.2017.19.016 http://www.tcsae.org

Liu Jintao, Zhang Shaohui, Xu Di, Bai Meijian, Liu Qunchang. Coupled simulation and validation with fully implicit time scheme for free-surface-pressurized water flow in pipe/channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(19): 124－130. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.19.016 http://www.tcsae.org

Coupled simulation and validation with fully implicit time scheme for free-surface-pressurized water flow in pipe/channel

Liu Jintao1,2, Zhang Shaohui1※, Xu Di1, Bai Meijian1, Liu Qunchang1

(1., 100038;2.100083,)

In the irrigation water distribution system including pipe and cannel as well as control valve/gate, water flow presents both free surface and pressurized flows. Saint-Venant equations are often applied to discribe the free-surface-pressurized water flow in pipe/channel by means of Preissmann slot approach and then four-point implicit finite difference and vector-dissipation finite-volume approaches with explicit-time scheme are applied to simulation of unsteady flow in pipe/channel. However, it is very different for gravity diffusion wave in free-surface water flow and pipe elastic wave in pressure water flow, which induces different constraint on time step size, low computational efficiency and large water balance error in the modes based on these 2 numerical solutions. To solve these problems, Saint-Venant equations was applied to describe the free surface and pressure water flows in irrigation water distribution system, conjunctive with the Preissmann slot approach. Then a scalar-dissipation finite-volume scheme was developed to spatially discretize all terms of the governing equations. This scheme exhibited more simple expression and was more suitable to written computational code than the four-point implicit finite difference approach and vector-dissipation finite-volume approaches. On the basis of the spatial scheme, a fully implicit time scheme was implemented to temporally discretize all terms of the governing equations to result in a nonlinear algebraic equation system. To efficiently solve this nonlinear algebraic equation system, a dual time approach was introduced, which included real- and pseudo-time steps, to make a linearization. The advantage of the dual time approach was the existence of a ratio between real- and pseudo-time steps. The value of the ratio could be automatically adjusted according to the known pipe water flow conditions and then the coefficient matrix of the algebraic equation system could maintain diagonally dominant all the time. In such case, the absolute convergence could be achieved whether free surface or pressurized flow was in pipe according to numerical analysis theory. As a result, a fully coupled model of free-surface-pressure flow for irrigation water distribution system was proposed. A standard physical test, which strictly controlled the initial and boundary conditions under the indoor condition, was firstly applied to validate the performance of the proposed model. The validated results showed that the proposed model could well simulate the free surface and pressurized water flow processes, which was similar to vector-dissipation finite-volume approach and better than four-point implicit finite difference approach. Meanwhile, the water balance error of the proposed model was only 0.16%. By contrast, the error values of the models based on four-point implicit finite difference and vector-dissipation finite-volume approaches were 2.1% and 1.2%, respectively. The computational efficiency of the proposed model was 1.3 and 5.2 times higher than the existing 2 models. Furthermore, a field experiment was performed in Hebei Yehe irrigation area, April 5, 2013. On the basis of the field observed data, the proposed model still exhibited better performance than the 2 existing models. In details, the water balance error of the proposed model was only 0.016%, by contrast, 2.68% and 1.35% for the 2 existing models. The efficiency of the proposed model was still 1.3 and 5.2 times higher than the existing 2 models. Consequently, the proposed model overcomes the disadvantages of the existing models and is suitable to practical engineering, and provides a useful method for tool design, evaluation and management of water distribution system in irrigation area.

irrigation; water piping systems; finite difference method; free-surface-pressurized water flow; fully implicit time scheme; coupling; simulation

10.11975/j.issn.1002-6819.2017.19.016

S275; S11+.1

A

1002-6819(2017)-19-0124-07

2017-05-02

2017-08-10

国家科技支撑计划课题（2015BAD24B01）

刘锦涛，山西沁源人，博士生，从事灌溉管网水动力学模拟与试验分析研究。Email：ljtpenny@163.com

※通信作者：章少辉，河北石家庄人，高级工程师，博士，从事灌区水循环动力学耦合模拟与调控研究。Email：zhangsh@iwhr.com