基于双难题的数字签密方案研究

周 克 元

(宿迁学院文理学院 江苏 宿迁 223800)

基于双难题的数字签密方案研究

周 克 元

(宿迁学院文理学院 江苏 宿迁 223800)

针对基于离散对数和因子分解双难题设计数字签密方案的问题，给出了一个使用Hash函数的签密方案。针对Hash函数存在被攻击的危险，给出了一个不使用Hash函数的签密方案。两个方案均具有抗伪造签名攻击、前向安全性和公开验证性。通过安全性分析和复杂度分析，与各类数字签密方案比较，复杂度更低。

离散对数 因子分解 数字签密 Hash函数

0 引 言

数字签名技术是实现网络身份认证、 数据完整性保护和非否认服务的基础， 是电子商务、电子政务等的重要工具，是密码学的研究热点之一。数字签名方案在使用过程中要经过签名和加密两个阶段。数字签密由Zheng[1]最早提出，数字签密技术能够在一个合理的逻辑步骤时间内，同时完成数字签名和公钥加密功能，并且复杂度和计算量要低于传统的先签名后加密，是同时实现保密和认证的传输消息的比较理想的方法[2]。

数字签密技术依赖的数学难题主要有离散对数、因子分解和椭圆曲线离散对数数学难题，目前数字签密方案大部分是基于单数学难题，如文献[1-10]中方案。对于基于单数学难题的签密方案，若该难题可解则签密方案不再安全。利用双数学难题设计数字签名方案没被攻击的目前有文献[11-12]中方案，双难题签名方案的实现还需结合加解密算法先签名后加密使用，复杂度较高。故寻找基于双难题的数字签密方案成为新的研究方向，目前对于该方向的研究成果较少，还没有相关算法方案。本文给出一个基于离散对数因子分解双难题的数字签密方案，方案中使用Hash函数，进行了安全性分析和复杂度分析。

Hash函数主要算法有MD5和SHA-1，王小云等[13-15]先后提出了MD5和SHA-1算法的杂凑碰撞，使得使用了Hash函数MD5和SHA-1的相关密码算法不再安全。关于使用Hash函数和冗余函数带来的威胁亦可见文献[17-18]，故第二类研究方向是设计不使用Hash或冗余函数的数字签密方案。目前已有的基于离散对数不使用Hash函数的签密方案主要有文献[19-22]中方案，对于基于双难题设计签密的方案较少，本文给出一个基于双难题同时不使用Hash函数和冗余函数的签密方案，进行了安全性分析和复杂度分析。

双难题相关理论如下：

引理1[16]大素数p，n=p1q1，n|(p-1)，其中p1、q1为大素数。g∈GF(p)，且g的阶为n，设由元素g生成的乘法群为G。对于∀y∈G，同余方程y=gx2modp的求解等价于离散对数方程y=gumodp的求解和二次同余方程x2=umodn的求解，而二次同余方程x2=umodn的求解等价于对整数n进行因子的分解运算。

1 基于双难题使用Hash函数的签密方案(方案1)

1.1 参 数

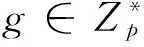
1.2 签 密

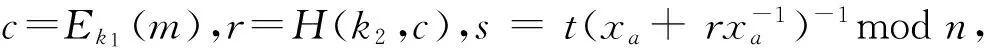
1.3 解签密

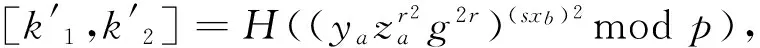
1.4 正确性证明

2 安全性证明

2.1 对抗公钥求解私钥的攻击

攻击者从同余方程ya=gxa 2modp中求解私钥xa，由引理1知，其数学难度相当于求解因子分解问题和求解离散对数问题。

在上述三个回归方程中，我们并不能排除误差项与解释变量之间的内生性问题。但如果这些无法观测到的因素不随时间变化，那么这些面板数据的固定效应将会是一致的。表3依次做了三个模型中固定效应和随机效应的Hausman检验，以确定使用具有随机效应还是固定效应的面板模型。豪斯曼检验结果是强烈拒绝原假设（详见表3中 Hausman test栏）。因此，我们认为本文使用具有固定效应的面板计量模型是恰当的。

2.2 对抗签密方程求出密钥的攻击

2.3 对抗离散对数问题可计算的攻击

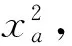
2.4 对抗因子分解可计算的攻击

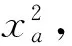
2.5 前向安全性分析

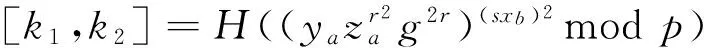
2.6 公开验证性分析

3 复杂度分析

使用Hash函数的基于离散对数单难题数字签密最新的方案是Li方案[5]，基于离散对数银子分解双难题数字签名最新的方案是Zhou方案[11]，将本文方案1与上述两种方案进行复杂度比较。结果见表1。

表1 复杂度比较

本文方案1运算复杂度比Li方案少2次模指数运算，与Zhou方案相同，签密长度相同，但Zhou方案签名需加密后再发送，本文方案1不需加密直接发送，故运算复杂度本文方案1更低。注：点积运算和Hash函数运算计算量较小，相对于模指数和模逆可忽略不计。

4 基于双难题无Hash函数的签密方案(方案2)

4.1 参 数

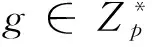
4.2 签 密

4.3 解签密

4.4 正确性证明

方案正确性证明如下:

所以

则该方案的验证过程是正确的。

5 安全性分析

5.1 对抗公钥求解私钥的攻击

攻击者从方程ya=gxa 2modp中求解私钥xa，由引理1可知，其数学难度相当于求解因子分解问题和求解离散对数问题。

5.2 对抗签密方程求出密钥的攻击

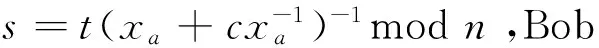
5.3 对抗离散对数问题可计算的攻击

5.4 对抗因子分解可计算的攻击

5.5 前向安全性分析

可类似于2.5节中相关证明证明方案2的前向安全性方法。

5.6 公开验证性分析

6 复杂度分析

基于离散对数单难题不使用Hash函数和冗余函数的数字签密方案最新的是Li方案[22]，基于离散对数因子分解双难题使用Hash函数的数字签密方案最新的是本文方案1，将本文方案2与上述两种方案进行复杂度比较。结果见表2。

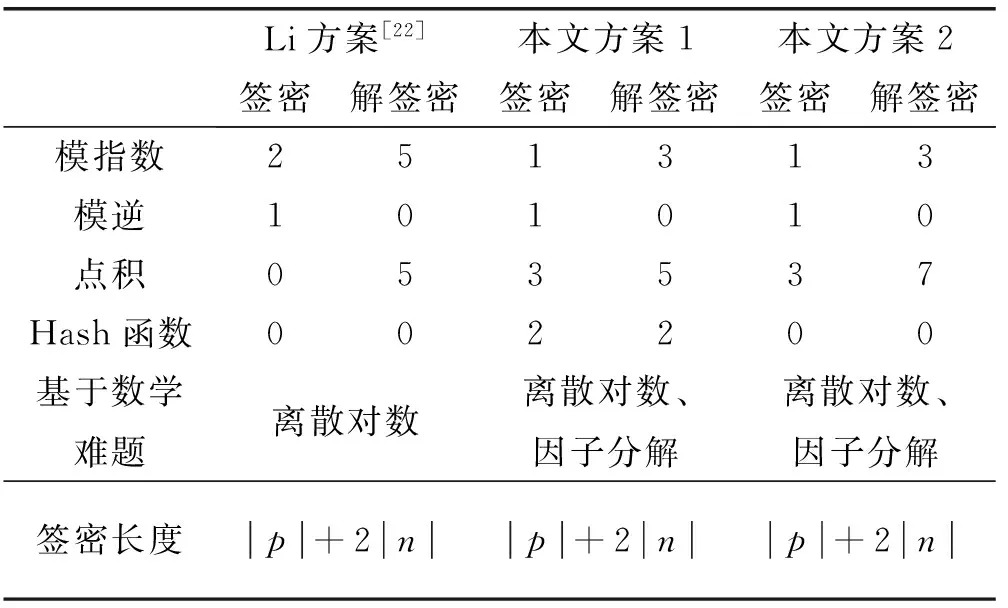
表2 复杂度比较

本文方案2与Li方案[22]相比，减少3次模指数运算，与本文方案1相比运算复杂度相同，签密长度与前两者签密长度均相同。注：其中的点积和Hash函数运算相对于模指数和模逆运算量较少，可忽略不计。

7 结 语

与先签名后加密相比，签密的最大的优势在于减少了计算量和通信量，适合大量数据的认证传递[1,3]。本文对基于身份的双难题数字签密进行了研究，对使用Hash函数和不使用Hash函数分别给出了一个签密方案，进行了正确性和安全性证明，并进行了复杂度分析，安全性与复杂度比已有的方案均更优。

[1] Zheng Y L.Digital signcryption or how to achieve cost (signature and encryption)[C]//Advances in Cryptography,Proceedings of CRYPTO’97,LNCS1294.London,UK:Springer-Verlag,1997:165-179.

[2] 李发根,胡予濮,李刚.一个高效的基于身份的签密方案[J].计算机学报,2006,29(9):1641-1647.

[3] Zheng Y L.Signcryption and Its Applications in Efficient Public Key Solution[C]//Berlin:Proceedings of Information Security Workshop(ISW’97),LNCS1397,Springer-Verlag 1998:291-312.

[4] Lee M K,Dong K K.An authenticated encryption scheme with public verifiability[C]//Proc of Japan Korea Joint Workshop on Algorithms and Computation. Tokyo[sn],2000:49-56.

[5] 李艳平,谭示崇,王育民.一个公开可验证和前向安全的签密方案[J].计算机应用研究,2006,23(9):98-99.

[6] 张串绒,肖国镇.一个可公开验证签密方案的密码分析和改进[J].电子学报,2006,34(1):177-179.

[7] 喻琇瑛,赖欣,何大可.一个可公开验证且前向安全的签密方案[J].计算机应用研究,2009,26(1):359-260.

[8] 张建航,胡予璞,齐新社.具有前向安全性和公开可验证性的签密方案[J].计算机应用研究,2011,28(2):733-734.

[9] 王天芹.一个基于椭圆曲线的可证明安全签密方案[J].计算机应用研究,2010,27(3):1055-1057.

[10] 于刚,黄根勋,王旭,等.基于椭圆曲线的可公开验证和前向安全的签密方案[J].信息工程大学学报,2008,9(3):21-23.

[11] 周克元.一个新的基于离散对数和因子分解的数字签名[J].科学技术与工程,2013,13(26):7862-7864.

[12] 周克元.基于椭圆曲线和因子分解双难题的数字签名方案[J].计算机科学,2014,41(6A):366-368.

[13] Wang X,Lai X,Feng D,et al.Cryptanalysis of the hash functions MD4 and RIPEMD[C]//International Conference on Theory and Applications of Cryptographic Techniques.Springer-Verlag,2005:1-18.

[14] Wang X,Yu H.How to break MD5 and other hash functions[C]//International Conference on Theory and Applications of Cryptographic Techniques.Springer-Verlag,2005:19-35.

[15] Wang X,Yin Y L,Yu H.Finding Collisions in the Full SHA-1[C]//International Conference on Advances in Cryptology.Springer-Verlag,2005:17-36.

[16] 邵祖华.基于因数分解和离散对数的数字签名协议[J].信息安全与通信保密,1998(4):36-41.

[17] Chien H Y.Forgery attacks on multi-signature schemes for au-thenticating mobile code delegates[J].IEEE Transactions on Ve-hicular Technology,2002,51(6):1669-1671.

[18] Dobbertin H.The status of MD5 after a recent attack[J].CryptoBytes,1996,2(2):1-6.

[19] Lee W,Chang C.Authenticated encryption scheme without using a one-way function[J].Electronics Letters,1995,31(19):1656-1657.

[20] Chen K.Signature with message recovery[J].Electronics Letters,1998,34(20):1934.

[21] 于永,綦朝晖.一种基于前向安全的可公开验证签密方案[J].计算机应用与软件,2010,27(1):283-285.

[22] 李方伟,闫少军,万丽.新的不使用冗余和Hash的安全认证加密方案[J].计算机工程与应用,2011,47(28):86-88.

ANALYSISONDIGITALSIGNCRYPTIONSCHEMEBASEDONDISCRETELOGARITHMSANDFACTORING

Zhou Keyuan

(SchoolofLiberalArtsandScience,SuqianCollege,Suqian223800,Jiangsu,China)

The problem of designing digital signcryption scheme based on discrete logarithm and factoring is discussed, and a signcryption scheme using Hash function is given. In addition, a signcryption scheme that does not use Hash function is given in view of the danger of Hash function being attacked. Two schemes have the characteristics of unforgeability, forward security and public verifiability. Security analysis and complexity analysis show that the complexity of the scheme is lower than that of various digital signcryption schemes.

Discrete logarithm Factorization Digital signcryption Hash function

TP309.7

A

10.3969/j.issn.1000-386x.2017.10.056

2016-12-27。宿迁市科研项目(Z201450)。周克元，讲师，主研领域：密码与编码。