基于正交拉丁方理论的数字签名分组批量验证

王宏，赖成喆，刘向阳，曾晗

（1.国防科技大学信息通信学院，陕西 西安 710106；2.西安邮电大学网络空间安全学院，陕西 西安 710121）

0 引言

随着无线通信、传感器及人工智能等技术的不断进步，各种态势感知网络在气象水文监测、城市智慧交通、能源在线监测等方面发挥着越来越重要的作用。技术进步带来便捷的同时，也导致人们受制于技术，尤其是个人信息的被盗、冒充或伪造等现象时有发生，极易造成态势感知网络的不畅，甚至瘫痪。因此，如图1 所示，对网络传递的消息进行签名，确保消息的可靠性、完整性和不可抵赖性成为一种重要的网络安全措施。传统的数字签名采用逐一验证方法，当中心型节点验证的签名数量较少时，逐一验证方法尚且可以适应要求；当需要验证的签名数量巨大时，逐一验证需要消耗大量时间，导致大量消息由于不能及时得到验证而被迫丢弃，比如庞大的车联网系统每隔100～300 ms 就要实时地进行消息传输，大量的消息连同附带的签名涌向中心节点等待马上验证[1-2]，以保证它们来源的可靠性。因此，有关数字签名的快速验证算法的研究成为近年密码学的研究热点。

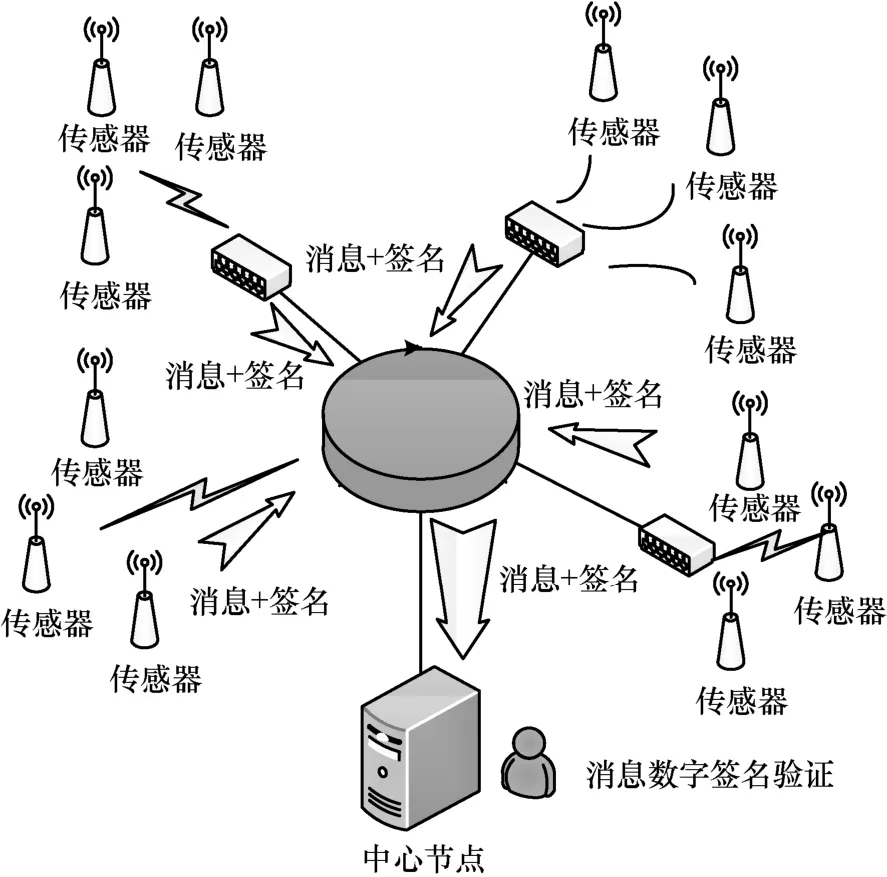
图1 中心型网络消息汇聚

围绕数字签名快速验证算法，研究者所做的工作归纳为2 个方面：一是数字签名的批量验证算法研究；二是分组检测方案设计。数字签名的批量验证通常采取聚合签名算法，聚合签名是将具有同态结构的签名算法进行聚合验证，达到一次性验证多个数字签名的目的，基于模指数运算的数字签名算法（DSA,digital signature algorithm）就具有这种同态结构[3-7]。近年来，许多聚合签名研究成果实现并证明了签名密钥的生成、分发和数字签名的聚合验证[8-11]，但聚合签名只能批量检测多个数字签名的集合中是否存在非法数字签名，不能鉴别非法数字签名在集合中的具体位置。为此，研究者纷纷引入已在生物医学检测中广泛应用的分组检测理论进行数字签名的分组检测。当数字签名集合中存在非法数字签名时，通过将数字签名分成不同的组，分组实施批量验证，从而逐步确定非法数字签名。

分组检测方案是针对数字签名聚合验证存在至少一个非法数字签名而进行非法对象识别的分组聚合验证方法，按照分组之间的关系，可以分为序贯类分组检测和非适应性分组检测[12]。序贯类分组检测是按照一定规则对检测对象进行“多次”有序分组检测，直到所有非法对象被全部识别。但在序贯类分组检测中，前一次检测的结果决定后一次分组的情况，检测过程具有严格的顺序性，只能一步一步按照分组顺序完成，如基于二元分叉树的分组检测。非适应性分组检测是根据一定规则巧妙地将检测对象“一次性”分成若干组，同一检测对象可以包含在多个组中，使检测具有一定数量的对象析取性，便于采用平行检测的方法对各组进行同时检测，并通过检测结果的呈现情况析取非法数字签名[3]。序贯类分组检测简单、实现容易，但运算效率很难提高[13-14]。非适应性分组检测可以并行检测，在多处理器的情况下，运算效率较高，但分组方案构造复杂。现有的非适应性分组检测算法具有以下3个特点：一是分组检测的次数、时间等参数界限研究探索较多[15-16]，而具体方案构造研究成果较少；二是分组检测方案构造不准确，存在非法数字签名不能完全析出的情况，如随机矩阵法[12]；三是分组检测方案的存在性理论缺乏严格证明，如基于纠错码（ECC,error correction code）的分组方案构建，缺少检测对象数量变化时的分组方案存在性证明[3,17-18]。

综上所述，本文针对数字签名的快速验证问题，研究分组批量验证算法，基于拉丁方理论构造分组方案，以较少次数的群组认证完成非法数字签名的识别，实现多个消息数字签名的快速验证。本文主要贡献如下。

1) 采用拉丁方理论构建横截设计。以有限域理论为基础设计素数幂阶拉丁方，证明素数幂阶拉丁方存在性是横截设计存在的充分必要条件，为数字签名分组批量验证方案确立提供理论基础。

2) 基于横截设计理论构建析取矩阵。证明当横截设计TD[k,;λm]的λ=1 时，其关联矩阵M的转置矩阵MT是一个析取矩阵，将区组设计与析取矩阵联系起来，为析取矩阵的构建提供具体方法。

3) 通过析取矩阵理论确定分组方案。以析取矩阵的列向量选择性为基础，根据检测对象的总数量以及其中包含非法者的数量确定析取矩阵的阶数，并由此构建分组检测方案，完成检测，根据分组检测结果推断非法数字签名在集合中的位置。

4) 对所提数字签名分组批量验证方案进行理论分析与仿真验证。理论分析证明了所提方案的正确性、安全性、高效性，并以Linux Ubantu20 为平台、Python3.9 为编程语言，引入双线性对函数库pypbc，基于成熟的BGLS 聚合签名算法[19]进行数字签名批量验证，仿真实现分组检测算法并识别非法对象。结果表明，所提方案能准确可靠地识别非法对象，同时在多个处理器并行计算时相较其他算法检测效率有所提高。

1 相关知识

本节介绍析取矩阵、区组设计、关联矩阵等非适应性分组检测的相关概念和背景知识。析取矩阵[12]用于非适应分组检测方案的非法数字签名的识别分析；区组设计[20]用于构造非适应性分组检测方案；关联矩阵[21]用于区组设计的矩阵化表示，是区组设计研究的一个有力的代数工具。

定义1d阶析取矩阵[12]。对于0-1 矩阵Mt×n，若任意d列的并集不包含其他列向量，即，则称Mt×n为d阶析取矩阵。换句话讲，对于任意d+1 列，必然存在至少一行（不妨设为第i行），使d列的元素mij=0，即并集=0，而

定义2区组设计[20]。有限集合X上的任意一个子集族B={B1,…,Bt}为X上的一个区组设计，记作D={X,B}。X称为此设计的基集，而子集族B中的诸子集Bi(i=1,…,t)则称为此设计的区组。

常见的区组设计包括成对平衡设计（PBD,pairwise balanced design）、可分组设计（GDD,group divisible design）、横截设计（TD,transversal design）、平衡不完全区组设计（BIBD,balanced incomplete block design）等[22]，本文主要应用横截设计进行区组设计。

定义3横截设计[22]。对于区组设计D={X,B}，若有限集合X的一个划分为G={G1,…,G k}（其中Gj,j=1,…,k称为组），且满足以下三点。

1) 对任意B∈B，=k。

2) 对任意Gj∈G，=m。

3)X中属于同一组的不同元素在区组中的相遇数λD(x,y)总为零，而属于不同组的2 个元素x,y的相遇数λD(x,y)是不依赖于x,y的常数，即对于任意x,y∈X，x≠y，有

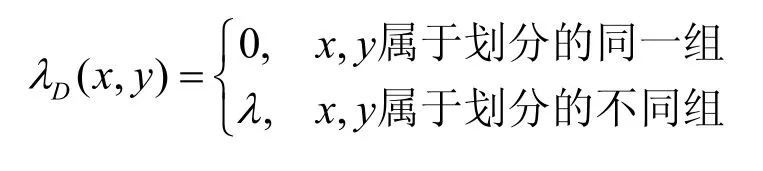
则称其为横截设计，记作TD[k,λ;m]。

定义4关联矩阵[21]。对于区组设计D={X,B}，其中有限集合X={x1,…,xn}及其子集族B={B1,…,Bt}，存在 0-1 矩阵Mt×n={mij}，i=1,…,t，j=1,…,n，t表示区组个数，n表示基集X元素个数，且

则称Mt×n为区组设计的关联矩阵。

2 非适应性分组检测模型

根据分组检测对象数量进行区组设计，构建非适应性分组检测模型，关键在于寻找相应的析取矩阵，本文首先运用拉丁方理论进行区组设计——横截设计，然后证明构造的横截设计对应的关联矩阵是析取矩阵，最后再运用析取矩阵进行分组检测，完成非法对象的识别。

2.1 基于拉丁方理论的横截设计

横截设计是构造区组设计的重要方法之一，它与正交拉丁方理论有着密切关系。正交拉丁方是组合设计的一个重要研究课题，在横截设计的递归构造方法中，正交拉丁方组对于横截设计的存在性起着十分关键的作用。下面首先介绍正交拉丁方的一些概念和基本性质，然后论证它与横截设计的关系，最后给出正交拉丁方的构造方法，从而完成横截设计的构造。

定义5拉丁方[22]。设S是一个m元集，若A为S上的一个m×m阶阵列（即矩阵），其每一行与每一列都是集合S的一个全排列，则称A是S上的一个m阶拉丁方。

定义6正交拉丁方[22]。对于集合S和S′上的2 个m阶拉丁方A=(aij)和B=(bij)，A和B在(i,j)位置上的有序对(aij,bij)∈S×S′称为一个对子，A和B在全部m2个不同位置上的对子两两不同，即=m2，则称拉丁方A和B正交。若一组m阶拉丁方A1,…,At两两正交，则称其为一个正交拉丁方组。

对于矩阵

根据定义6，显然H与其转置矩阵G=HT正交。显然，若A是{1,…,m}上的任一m×m阶阵列，则A是m阶拉丁方的充要条件是A与H及A与G都正交。

定理1[22]存在TD[k,1;m]的充要条件是存在一个k-2个m阶正交拉丁方组。

证明令D=(X,G,B)是个TD[k,1;m]，根据TD 定义，则对任一B∈B 及任一Gj∈G，有=1，即任一区组B由每个组中各取一个元素组成。任取划分G的2 个不同的组G1和G2（划分的每个组中含有m个元素），由于B中的每个区组恰好包含了一个G1的元素和一个G2的元素，且由于λ=1，G1的元素和G2的元素在B的每个区组中总共相遇一次，因此B的区组数等于G1中所有元素和G2中所有元素的相遇总次数，即

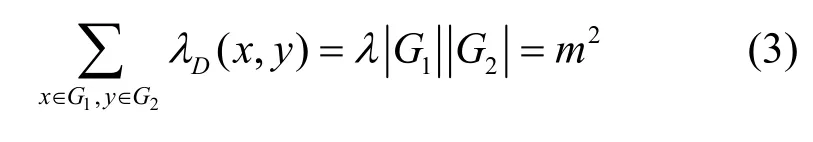
因此，B中共有m2个区组，G1的m个元素和G2的m个元素在B的每个区组中仅仅相遇一次，故G1和G2元素在区组设计B 中组成的有序数对{(g1,g2)|g1∈G1,g2∈G2}仅仅出现一次可以看成{1,…,m}上2 个正交的阵列，那么G1,…,G k的元素在区组设计B中两两组成的有序数对仅仅出现一次可以看成{1,…,m}上两两正交的阵列，除了H和G，则一定还存在k-2个正交拉丁方。

反之，若存在k-2 个m阶正交拉丁方，加上H和G，便可以构造k个两两正交的m阶阵列组，这些阵列两两之间每个元素对仅仅出现一次，照此便可以构造出一个TD[k,1;m]。证毕。

然而，并不是任意阶的正交拉丁方都是存在的，Bose、Shrikhande 和Parker 三人经过共同努力，证明了若n≠2,6则必定存在一对拉丁方。由上述定理可知，在构造横截设计时，需要尽可能多的拉丁方。根据有限域存在定理[23]，对于任意素数幂pτ，存在一个含有pτ个元素的有限域，显然TD[k,1;m]的约束和有限域的特征非常相似，下面介绍通过有限域构造正交拉丁方组的方法。

则 (e1-e2)i=(e1-e2)k。

由于e1≠e2，故(e1-e2)-1，因此i=k，代入可得j=l。

综上所述，A(1),A(2),…,A(m-1)是两两正交的拉丁方组。证毕。

2.2 基于横截设计的析取矩阵

析取矩阵是一类二元叠加码，可以用作分组检测的一种数学模型，广泛应用在信息传输中的多路存取信道、分子生物学、基因遗传测试、病毒分组检测等诸多方面，横截设计TD[k,1;m]关联矩阵M的转置矩阵具备析取矩阵的特征，以下将从理论上证明这种推断。

在t行n列的0-1 矩阵M中，Cj表示第j列向量；wj表示第j列向量Cj的重量，即Cj中“1”的个数；λij表示列向量Ci与Cj的点乘，即Ci与Cj相同行上都为1的个数，也称为Ci与Cj相交λij次。

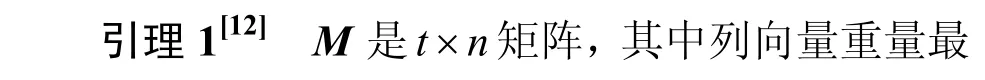
定理3当TD[k,;λm]设计的λ=1 时，其关联矩阵M的转置矩阵MT的λT=0 或1，则MT是k-1阶析取矩阵。

证明当λ=1 时，TD 区组设计对应关联矩阵M的任意两列的内积为1，即M的任意两列仅仅有一次在相同位置（行）都为“1”，则M的任意两行元素仅仅有一次在相同位置（列）都为“1”，下面用反证法进行证明。假设M的任意两行元素至少有两次在相同位置（列）都为“1”，此时M的任意两列元素至少有两次在相同位置（行）都为“1”，与λ=1相矛盾，故M的转置矩阵MT的λT=0或1，则=1，此时，由引理1可知MT是k-1（即w-1）阶析取矩阵。证毕。

2.3 基于析取矩阵的分组检测

采用分组检测进行数字签名验证，将数字签名进行分组，分组结果用关联矩阵Mt×n表示，其中矩阵的列对应要检验的数字签名，矩阵的行对应分组，Mt×n中元素{mij}的取值参考定义4。

不妨假设将要进行分组批量验证的数字签名集合Σ=(σ1,…,σn)的状态为X=(x1,…,xn)，其中xi(i=1,…,n)表示每个数字签名的实际状态，xi=0表示第i个数字签名合法，xi=1表示第i个数字签名非法。为了快速进行数字签名验证，运用2.1 节的横截设计对数字签名进行分组，并行进行分组检测，用Y表示分组检测结果，记为Y=(y1,…,yt)，其中yj=0(j=1,…,t)表示本组检测的数字签名集合全部合法，yj=1(j=1,…,t)表示本组检测的数字签名集合至少包含一个非法数字签名，它与X和Mt×n的关系可以表示为

根据2.2 节的证明，上述分组批量检测区组设计的关联矩阵Mt×n为d阶析取矩阵，当数字签名集合X中非法数字签名的个数不超过d时，运用算法1 便可以确定非法数字签名。

算法1非法数字签名分组检测法

3 数字签名分组检测实施

网络的中心节点每秒接收到大量节点发来的消息，为加快消息签名的验证速度，通常采用“聚合签名+分组检测”的方法进行数字签名的验证，如图2 所示。首先采用聚合签名算法将所有来自不同节点的消息签名设计为具有同态性特征，便于后续聚合验证作为中心节点的信息处理中心先将所有消息及其签名进行一次聚合验证，若验证成功，则表明所有消息合法；否则，证明消息集合中至少存在一个非法对象，需要进一步采取非适应性分组的思想进行分组聚合验证，用i表示分组序号，i取遍t个分组，通过分组验证的结果排除合法对象，从而确定非法对象，当出现无法确定的对象时还可以补充进行个体认证。由此可见，实现消息签名批量验证的是聚合签名算法，识别非法对象依靠分组检测，不同的分组方案对应着不同的识别效率。

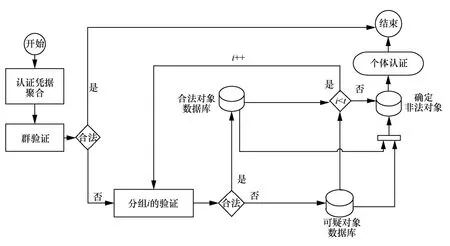
图2 数字签名快速验证方法

3.1 聚合签名

为提高数字签名的验证效率，在一般数字签名算法的基础上，杨涛等[8]提出一种具有同态性结构的变体数字签名算法，验证者能够将来自任意不同节点的多个数字签名压缩合成为与单个数字签名几乎同等大小的短签名进行批量验证，大大减小了多个签名验证的工作量，这就是聚合签名。聚合签名由于其高效性、简捷性，广泛应用于安全路由协议、网云信息聚合、日志审计、分布式计算等方面，在诸多信息科技领域发挥着重要的安全保护作用，成为近年来被关注的一个研究热点。本文采用经典的BGLS 聚合签名算法[19]完成消息签名的批量验证，下面对该算法进行阐述。

设G1和G2是2 个p阶的乘法循环群（p为素数），g1和g2分别是G1和G2的生成元；ψ:G1→G2是一个同构映射，且ψ(g1)=g2；e:G1×G2→GT是一个双线性对运算；h:{0,1}*→G2是一个杂凑函数，可以看作一个随机预言机。

密钥生成。选择随机数x∈RZp，计算v=则v∈G1作为用户的公钥，x∈Zp作为用户的私钥。

签名生成。对于用户u i∈U，公钥为vi，私钥为xi，需要签名的消息为Mi∈{0,1}*，可得hi=h(Mi)，σi=。

BGLS 聚合签名算法的安全性等价于随机预言模型下CDH（computational Diffie-Hellman）问题的安全性。

3.2 实施步骤

假设检测n=m2（m为素数或素数幂）个数字签名集合，其中含有不超过d=k-1个非法数字签名，根据拉丁方理论便可以构造一个横截设计TD[k,1;m]，当m＞k时，通过km次分组检测完成m2个数字签名的验证，识别出非法数字签名，如图3所示，具体步骤如下。

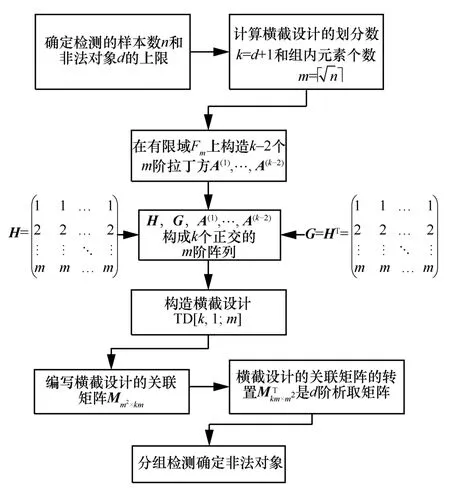
图3 数字签名分组检测实施步骤

步骤1确定分组检测参数设置。根据需要检测的数字签名集合大小n以及非法对象数量上限d，确定横截设计TD[k,1;m]的参数(k,m)，如果数字签名的总数及非法对象的个数不满足上述要求，可以进行适当的冗余填充，达到要求。

步骤2构造k-2个正交拉丁方。采用定理2构造k-2个m阶正交拉丁方A(1),…,A(k-2)。

步骤3由H,G,A(1),…,A(k-2)构造TD[k,1;m]。

步骤4编写TD[k,1;m]的关联矩阵求出d阶析取矩阵

步骤5 按照进行分组检测，通过检测结果由算法1 推知非法数字签名。

3.3 举例说明

如果对25 个数字签名进行验证，据前期统计估计其中包含非法数字签名的数量不超过2 个，则令n=m2=52，d=k-1=2，则k=3，m=5，确定横截设计为TD[3,1;5]。

利用定理2 构造一个5 阶拉丁方矩阵

连同H和G，按照定理1的方法，由3 个拉丁方一起构成一个横截设计TD[3,1;5]，其关联矩阵为25 行15 列矩阵M25×15，转置后得到15 行25 列0-1 矩阵其中每列有3 个“1”，每行有5 个“1”，如图4 所示。

根据定理3可知，0-1矩阵TM为2 阶析取矩阵。图4 中的矩阵25 列表示需要验证的25 个数字签名，15 行表示25 个数字签名分成的15 个分组，矩阵中(i,j) 处的元素“1”表示j列的数字签名属于i行的分组；否则，表示不在此分组。析取矩阵的性质表明，按照图4 中分组方案进行批量验证，可以通过15 次分组检测对25 个数字签名完成不超过2 个非法对象的识别。

为了说明分组方案在数字签名批量验证中的使用思路，不妨假设第3、6 个数字签名是非法的，在图4 中用方框表示，按照分组方案调用聚合签名算法完成15 个分组的批量验证，得到检测结果Y=(1,1,0,0,0,1,0,1,0,0,0,1,1,0,0)T，由于15×25M是2 阶析取矩阵，Y中的“0”表示本组检测中所有数字签名均为合法，根据算法1，采用排除法可以依次确定合法数字签名x11、x12、x13、x14、x15、x16、x17、x18、x19、x20、x21、x22、x23、x24、x25、x2、x7、x4、x9、x5、x10、x1、x8，如图4 中下划线所示；根据析取矩阵的性质可知，剩下的签名x3、x6便为非法数字签名。

图4 15 个数字签名的分组验证的分组情况

4 性能分析

本节通过理论证明和仿真实验，对本文算法进行了可行性和复杂度分析，并对非法数字签名数量估计不准的情况讨论了方案的容错性；同时借助开源的双线性对计算函数库，编程实现了BGLS 聚合签名方案和本文算法，仿真验证了数字签名分组检测方案。结果表明，在相同安全要求下，本文算法相较于逐一验证具有高效性，即使与经典的二分法检测相比也具有明显的效率优势。

4.1 理论证明

1) 可行性分析

根据算法1的排除法可知，本文算法是通过分组检测结果中合法结果（即检测结果为“0”分组）选出合法数字签名，然后取合法数字签名对应的余集作为可疑签名集U=XV，若≤d则确定非法数字签名。之所以能够识别非法数字签名，是因为关联矩阵的析取性，下面根据析取矩阵的特性，对其进行证明。

定理4群组认证关联矩阵是d阶析取矩阵，则由分组检测的结果Y通过算法1 可以识别不超过d个非法数字签名。

2) 复杂度分析

本文算法对n个数字签名进行验证，初步估计非法数字签名的数量不超过d个。下面对本文算法的复杂度进行分析。

定理5 本文算法进行分组检测，通过个分组完成n个数字签名进行验证，非法数字签名识别算法（算法1）的时间复杂度为其中d为非法数字签名的数量上限，且d≪n。

证明要完成n个数字签名进行验证，根据3.2 节中的实施步骤，首先基于拉丁方构造了用于分组检测的析取矩阵MT，它的行数为km，列数为m2，由于k=d+1，n=m2，则

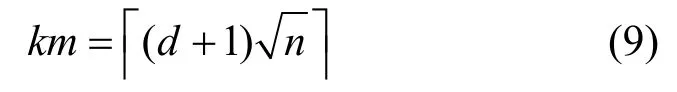
另外，当分组批量验证完成后，需要通过算法1运用排除法完成非法数字签名的识别，只有分组批量验证为“0”的分组才参与排除法，不妨用t0表示批量验证Y=(y1,y2,…,ykm)中为“0”的分组，根据横截设计的“0”“1”分布特征，关联矩阵MT的每列元素“1”的个数为k，分组批量验证结果Y=(y1,y2,…,ykm)便为MT的所有非法数字签名对应列的布尔和，因此结合非法数字签名的数量上限d，可知Y中“0”的个数满足

3) 容错性分析

容错性是指当非法数字签名数量估计不准确时，分组检测方案识别非法数字签名的能力变化情况。显然当非法数字签名的实际数量d′≤d时，关联矩阵MT为d阶析取矩阵的分组检测方案识别能力没有变化，因此重点讨论d′＞d的情况，此时分组验证的结果Y=(y1,y2,…,ykm)便为所有d′列元素的布尔和。因为关联矩阵MT为d阶析取矩阵，所以无法通过算法1 准确识别非法数字签名，却可以确定一个包含所有非法数字签名的更大的可疑对象集合，此时可以采用图1的方法对可疑对象进行逐一验证，从而完成非法数字签名的识别。具体举例如下，参照图4的关联矩阵，需要验证的数字签名个数仍为25，初步估计其中非法者的个数不超过2 个，但实际第3、11、17 个数字签名是非法的，利用上述分组检测得到检测结果Y=(1,0,1,1,0,1,1,1,0,0,0,0,1,0,1)T，由于15×25M是2 阶析取矩阵，Y中的“0”表示本组检测中所有数字签名均为合法，采用排除法可以依次确定合法数字签名x6、x7、x8、x9、x10、x21、x22、x23、x24、x25、x4、x14、x19、x5、x15、x20、x1、x18、x2、x6、x12、x16，剩下的数字签名x3、x11、x13、x17都为可疑对象；此时剩下的数字签名数量超过3，证明非法数字签名数量估计偏少，2 阶析取的关联矩阵无法完成非法数字签名的确定。如果剩余签名数量和初始估计的签名数量相差较大，则需要重新设计分组检测方案；否则，便可以逐一认证剩下的签名，确定非法对象。因此，逐一验证x3、x11、x13、x17便可以完成所有数字签名的验证。

4.2 仿真比较

为检验本文算法的实际性能，在处理器为Intel Core i5-4200 2.5 GHz、内存为4 GB的笔记本电脑的虚拟机VMware Workstation Pro 上安装Linux Ubantu20 操作系统，在Python 3.9 编程环境下基于GMP（GNU multiple precision）和PBC（pairing-based cryptography）配置pypbc 双线性对匹配加密库，杂凑函数采用SHA-256，仿真环境配置如图5 所示。

图5 仿真环境配置

基于BGLS 聚合签名方案进行数字签名的批量处理，以数字签名的数量n及其所含非法数字签名的上限d作为分组的依据，采用3.2 节的步骤进行分组检测，使用算法1 进行非法对象的识别，部分仿真结果如表1 所示。

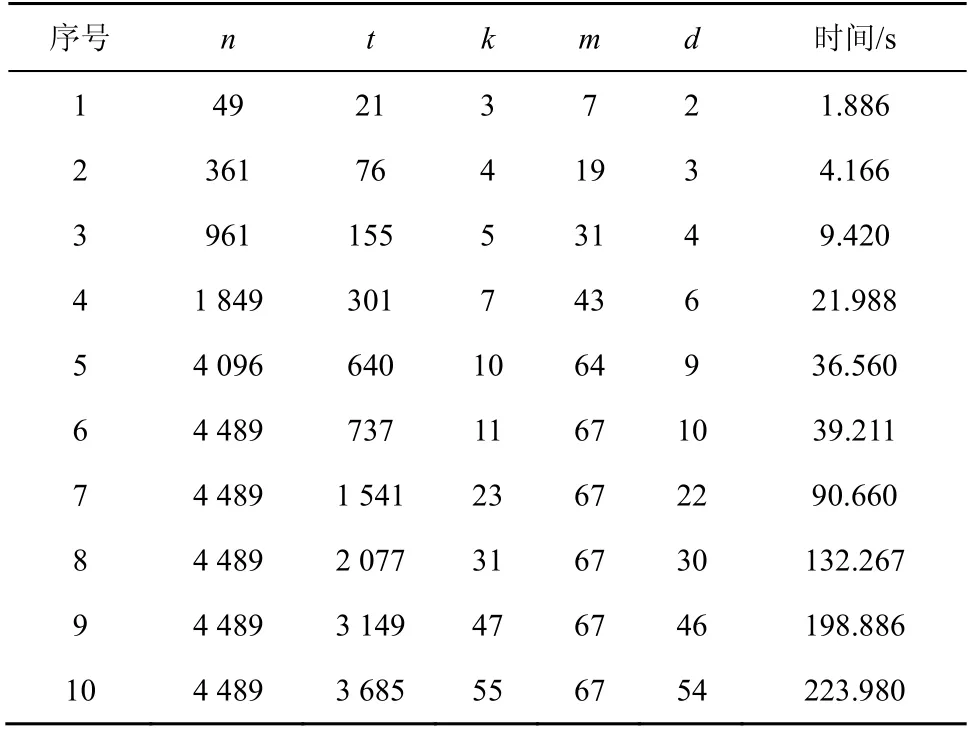
表1 数字签名分组检测部分仿真结果

分组检测的完成时间主要与分组检测次数相关，当数字签名的数量、非法数字签名的数量增加时，分组个数必然增加，如图6 所示。随着分组检测次数的增加，完成数字签名验证的时间也在增加，正如表1 所示。另外，从仿真实验中发现，当数字签名的总数n不变，但非法数字签名的数量增加到接近n/3 时，分组检测的效果低于逐一验证的效率，与文献[12]结论一致。

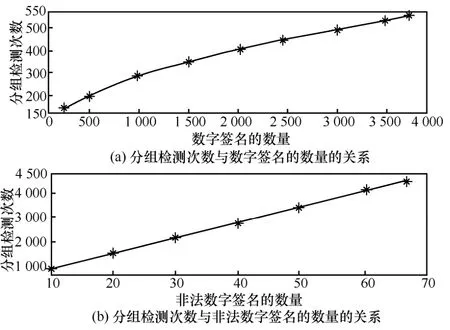
图6 分组检测次数与数字签名的数量、非法数字签名的数量的关系

非适应性分组检测方案与序贯性分组检测方案比较，一个重要区别在于分组平行处理，本文仿真采用Thread 函数进行平行检测处理，如表2所示。当数字签名的数量和非法数字签名的数量分别为n和d时，列出逐一验证、二分法验证和本文算法在不同处理器数量时的最大检测数量。逐一验证需要对每个签名进行一次验证，验证次数为n，在p个处理器工作的情况下，可以将数字签名分为p个分组，需要次检测；二分法验证采用折半查找法，每次需要次检验，只能检测一个非法数字签名，d个非法数字签名需要次检验，在p个处理器工作的情况下，可以将数字签名分为p个分组，分别进行折半查找，需要次检测；本文算法通过个分组完成n个数字签名中d个非法数字签名识别，在p个处理器工作的情况下，可以将数字签名分为个分组同时进行，需要次验证。

本文算法采用并行处理的设计思想，为便于验证的同时进行处理，设计了个独立并行的分组进行验证数字签名。从表2 可以看出，单个处理器时二分法验证效率最高，达到O(logn)，而本文算法的仅比逐一验证的O(n)较好一些。当多个处理器同时处理时，所有算法都可以并行处理，不管是逐一验证、二分法验证还是本文算法的检验效率都有所提高，本文算法的效率提升明显，提高到单个处理器时的p倍，而二分法验证提高了logn p倍，显然（通常n＞p）。

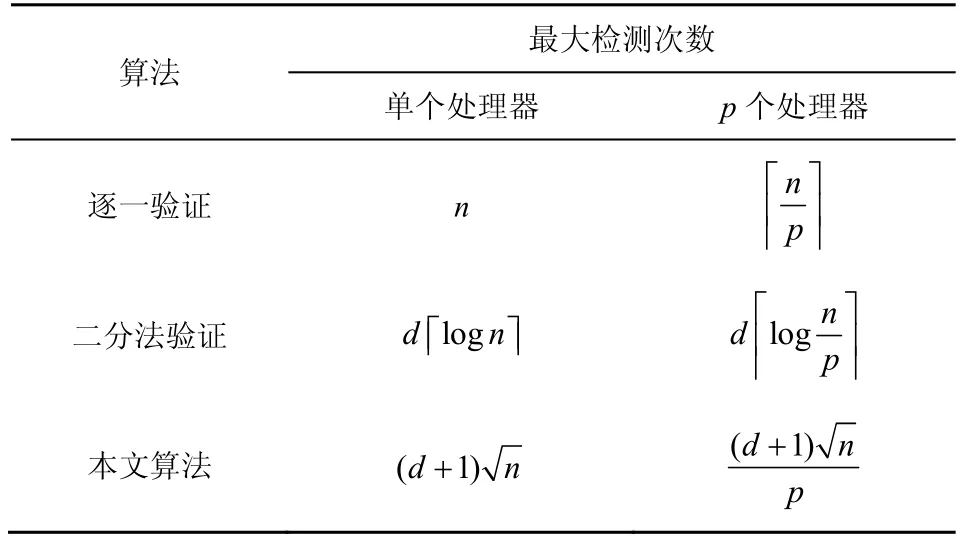
表2 数字签名分组检测比较

如图7 所示，将本文算法与逐一验证和二分法验证进行比较发现，当单个处理器串行验证时，二分法验证有相对较好的表现，同等数量的数字签名需要的验证次数最少；当多个处理器并行验证时，在非法数字签名数量d=8、处理器个数p=100的情况下，虽然逐一验证和二分法验证可以用多个处理器同时进行验证，效率有所提升，但是随着数字签名的数量增多，本文算法表现出较强的效率优势。当数字签名的总数大于3 000 时，本文算法与逐一验证相比才体现出优势，在多处理器保障的条件下，本文算法分组检测的次数随着数字签名总数的变化不大，基本上保持在8 附近，与二分法验证、逐一验证相比，具有最少的验证次数，效率最高。随着数字签名的数量不断增大，尤其是的增大，当多处理器并行验证时本文算法会表现出更多优势。

图7 分组检测次数与数字签名的数量的关系

5 结束语

数字签名的非适应性分组验证是为提高网络中心节点数字签名的验证效率，将组合设计理论与聚合签名理论相结合，以横截设计理论为基础设计数字签名分组方案，以聚合签名理论为方法完成数字签名的批量分组验证，实现数字签名的并行快速验证。它通常应用于传感器网、交通网、物联网等具有海量节点信息需要安全验证，且消息时敏性强的无线网络环境。本文基于组合数学的拉丁方理论设计了数字签名分组方案，并以经典的BGLS 聚合签名理论进行数字签名的批量验证，构建了一个以次数完成n个数字签名验证的非适应性数字签名分组验证方案。该方案与逐一认证相比具有较高验证效率；在多处理器保障的条件下，与序贯类分组方案相比具有验证次数少、效率高的优势。但本文研究未考虑数字签名在信道中的传输错误问题，需要进一步研究加入检错纠错机制，增强分组检测的容错性能。