无线网络多用户干扰下智能发射功率控制算法

张先超，赵耀，叶海军，樊锐

（1.东南大学移动通信国家重点实验室，江苏 南京 210096；2.嘉兴学院浙江省医学电子与数字健康重点实验室，浙江 嘉兴 314001；3.北京理工大学信息与电子学院，北京 100081；4.北京邮电大学信息与通信工程学院，北京 100876；5.中国电子科学研究院，北京 100041）

0 引言

近年来，随着移动互联网和人工智能技术的快速发展，智能手机、增强现实（AR,augmented reality）、虚拟现实（VR,virtual reality）等智能无线设备与远程医疗、工业4.0、自动驾驶等智能应用进入爆发式增长阶段，无线网络中出现了大量无线终端，且这些无线终端相较于现在的智能手机而言，对通信性能的要求更加苛刻与多元[1-2]。为了利用有限的频谱来满足未来的高性能要求，研究人员提出频谱共享[3]、D2D（device-to-device）技术[4]及超密集网络[5]等大幅提高频谱利用率的新技术，但这些技术在使用过程中不可避免地带来基站之间、基站与用户之间或多用户之间的互相干扰，而发射功率与干扰影响密切相关，功率低则相互干扰程度小，但自然通信质量差，功率高则会加剧相互干扰，因此，发射功率控制是降低相互干扰、保证多用户的通信服务质量与体验的有效途径[5]，也一直是通信研究的热点之一。

目前的发射功率控制算法研究方向主要有三类：1) 基于模型的优化算法，将发射功率控制问题转化为优化问题进行求解；2) 基于博弈论的方法，将发射功率控制问题转化为博弈问题进行求解；3) 基于机器学习的方法，将发射功率控制问题转化为机器学习相关的问题进行求解。下面分别对三类方法的研究现状进行介绍。

1) 基于模型的优化算法。文献[6-10]分别通过加权最小均方差（WMMSE,weighted minimum mean square error）算法、分数规划（FP,fractional programming）算法、连续凸逼近算法、内点法和最大化最小系统频谱效率准则的优化算法对功率控制问题进行适当转换与求解。以上算法通过采用优化理论求解系统最佳的功率分配，但由于干扰环境下的系统模型非凸，导致求解过程十分复杂，即使系统的性能提高，但是基于模型的优化算法的复杂度高，求解时间大于信道相干时间，结果难以在实际中应用[11]。

2) 基于博弈论的方法。文献[12-13]分别将D2D 网络中的功率控制问题建模为势博弈和Stackelberg 博弈，利用分布式方法最大化多用户的通信速率。基于博弈论的功率控制方法的优势在于其能够实现分布式决策，但博弈论追求稳定的纳什均衡状态，该状态并不能保证所求结果为全局最优解。

3) 基于机器学习的方法。最近兴起了基于机器学习的功率控制方法，这是由于机器学习在计算机科学领域的成功应用，使研究人员逐渐将机器学习技术应用在无线通信中[14]。文献[15]通过收集大量全局信道状态信息（CSI,channel state information），使用WMMSE 算法来产生功率分配集作为标签，使用全局CSI 集合与对应的标签进行深度神经网络（DNN,deep neural network）的训练直到收敛，训练完成后，可以将瞬时全局CSI 输入训练好的DNN，直接输出对应的最优功率分配策略。该方法需要消耗大量计算资源和时间成本来产生训练集并对深度神经网络进行训练，且在实际环境中很难收集到准确的全局信道状态信息来产生合理的训练集。文献[16]提出一种基于多用户深度Q 网络的算法，通过不断试错来优化功率分配策略，最终可以收敛到和WMMSE 接近的性能，但是该方法需要为深度神经网络输入大量状态信息且必须对功率进行离散化处理，无法施加连续动作。类似地，文献[17]提出一种分布式深度Q 网络方法来进行D2D 通信中的分布式功率与频谱分配，该方法能够有效提升动态环境下的D2D 通信性能，但仍然只适用于离散动作问题。文献[18]提出多种深度强化学习方法来解决频谱共享网络中的发射功率控制问题，次级用户能够获取主用户的功率分配信息，并结合传感器的接收功率强度值对自身的发射功率进行调整，最终满足通信网络的服务质量要求并实现有效的频谱共享。

本文针对多用户通信链路之间存在干扰的情况，考虑复杂的无线信道环境，提出了以深度强化学习“行动器-评判器”为基本架构的智能发射功率控制算法，对多用户发射功率进行有效控制，实现多用户通信速率最大化。该算法基于深度强化学习（DRL,deep reinforcement learning）技术，通过与环境不断交互、自我改进的学习方式来获得最优策略，不需要带标签的训练集；采用深度确定性策略梯度（DDPG,deep deterministic policy gradient）方法，使用2 个深度神经网络分别拟合行动器和评判器，并在训练过程中加入经验回放和目标参数软替代的方法，确保算法的收敛性；训练收敛后，利用行动器网络拟合出的最优策略，根据信道状态信息实时进行最优的功率控制。仿真结果表明，所提算法能够快速收敛，且在保证性能接近理论最优算法的前提下能够有效降低功率控制所需的运算时间。此外，算法性能不会随着网络规模的增加而下降，能够很好地适用于大规模无线网络。

1 系统模型

设有K对收发无线终端设备的无线通信系统，每对收发终端有一条通信链路，每条通信链路中的收发设备固定，且链路之间存在干扰，如图1 所示。

图1 链路有干扰的无线通信系统示意

假设第k条链路（1 ≤k≤K）的发射终端设备在时刻t的发射功率为Pk(t)，发射信号为xk(t)，其接收端的信号为

其中，hk(t)为时刻t第k条链路的复信道系数；h j,k(t)为时刻t第j条链路的发射机与第k条链路的接收机的复信道系数，即为时刻t第k条链路收到的来自其他链路的干扰信号；z k(t)为独立同分布的复高斯白噪声，噪声功率为N0。

其中，hj,k(t)和信道更新过程e j,k(t)均是独立同分布的单位方差循环对称复高斯随机变量。相关系数ρ=J0(2πfdT)，其中，J0(·) 是零阶贝塞尔函数，fd是最大多普勒频率。

对于其中一条通信链路的信号，其他发射机的信号将被视为噪声，该设备的接收信号速率也将取决于信干噪比（SINR,signal to interference plus noise ratio）。在给定信道状态信息H(t)和发射功率P(t)={Pk(t),∀k}的情况下，接收机k的接收数据速率为

依据式(3)，建立多用户发射功率控制的干扰管理问题的数学模型，如式(4)所示。

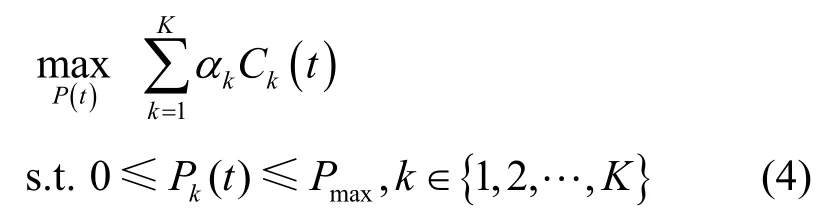
式(4)的目标是实现无线通信系统加权数据速率最大化，其中，αk是设备k对应的正值权重，表征链路重要性。

式(4)的优化变量同时存在于lb 函数的分子与分母中，该问题的优化目标函数复杂且非凸，该问题的求解一直是无线通信领域进行干扰管理的研究重点。现有的求解算法对模型依赖度高，且算法复杂度较高，难以适用于未来无线网络大规模多用户接入的复杂动态场景。

2 智能无线发射功率控制算法

考虑到发射功率控制为连续动作问题，采用深度强化学习的DDPG 方法[20]，构建智能无线发射功率控制算法，整体框架如图2 所示。

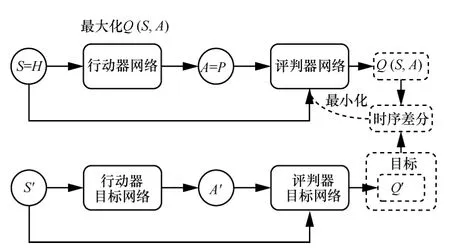
图2 智能无线发射功率控制算法整体框架

首先，由于无线信道环境具有马尔可夫性质，故在此将功率控制这一动态决策的过程建模为马尔可夫决策过程。设S=H为全局状态值，设a(t)={Pk(t)|0≤Pk(t)≤Pmax}k=1,2,…,K为动作集，在智能功率控制过程中，假设存在一个集中控制器能够收集全部信道状态信息，向智能体输入状态值；智能体将基于状态值与自身随机策略做出决策，输出具体动作（信道状态信息与功率控制信息一般通过控制链路传递，不占用数据链路带宽[21]），即a(t)～π(a(t)|S(t))，之后根据状态转移函数进入下一个状态S(t+1)～Pr(S(t+1)|S(t),a(t))。此外，智能体将得到一个对应的奖赏函数r(t)=r(S(t),a(t))，并得到自身对新状态的观测量S(t+1)。训练目标是追求最大化长期回报其中，γ为折扣系数，T为时间范围。

根据优化问题式(4)，可以将奖赏函数定义为

为了得到最佳的功率控制策略，强化学习需要不断试错，并迭代进行策略评估与策略改进[22]。深度强化学习则使用深度神经网络来进行策略评估与策略改进，分别对应评判器网络和行动器网络，但由于强化学习训练过程中前后序列的强相关性，传统的“行动器-评判器”算法难以收敛。为此，这里采用收敛性更优的深度确定性策略梯度方法。具体地，设行动器深度神经网络为μ（s|θμ），其中，θμ为行动器深度神经网络的权重系数，行动器目标神经网络选用不同的权重系数，目标行动器深度神经网络为。类似地，将评判器深度神经网络表示为Q(s,a|θQ)，其目标网络表示为，θQ和分别对应各自神经网络的权重系数。后续对神经网络的训练即对θQ和θμ这2 个权重系数的更新，更新的目的是使评判器网络能够对功率控制策略做出更精准的评估，使行动器网络输出价值更大，即系统传输速率更大的发射功率。

为了进一步提升训练效果，利用经验回放方法，增加搜索广泛性。每次在状态s(t)下根据策略施加动作a(t)=μ(s(t)|θμ)+ζ，其中，ζ为一个随机变量，作为动作噪声来增加探索性；之后达到新的状态s(t+1)，并获得相应奖赏r(t)。将此时的经验g(t)={s(t),a(t),r(t),s(t+1)}存入回放缓存，形成经验集，在训练神经网络时从回放缓存中随机选取批量经验进行学习，以此打破强化学习训练步骤前后的相关性，保证训练的稳定性和收敛性。

为了训练评判器神经网络，从回放缓存中随机采样N组经验，选用合适的优化器来最小化该批经验的期望预测误差（即损失函数），如式(5)所示。

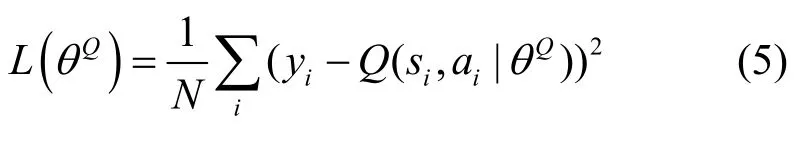
其中，yi为

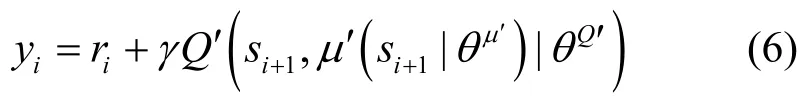
据此更新评判器神经网络的参数Qθ。目标评判器神经网络参数的更新则采取软更新方法，即

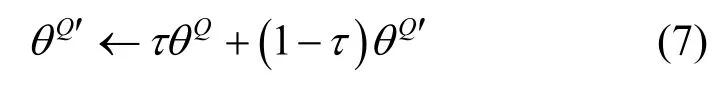
其中，τ∈ [0,1]是目标评判器网络的学习率。

行动器神经网络的训练目标是最大化价值函数Q(s,a|θQ)的期望，即

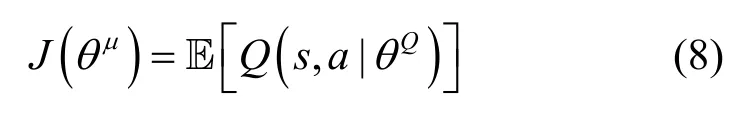
其中，E[]· 为期望函数。使用采样策略的梯度下降法更新参数，计算式(8)的梯度为

其中，∇表示求解函数梯度。同样地，目标行动器神经网络参数的更新也采取软更新方法，即

算法流程如算法1 所示。

算法1智能无线发射功率控制算法

3 仿真分析

3.1 仿真设计

设有10 对无线终端组成的无线通信系统，随机分布在直径1 km的区域内，通信总可用带宽为2 MHz，通信信道路径损耗为120.9 +37.6lbd（单位为dB，d为发射端和接收端之间的距离），多普勒频率为10 Hz，噪声功率N0=-174 dBm/Hz。文献[21]分别选取5 对和10 对收发机进行仿真验证，为更好地进行验证，本文也分别对5 对和10 对收发机进行仿真验证。发射机最大发射功率为1 W，总时间步长为0.1 s，分为100 个时间块，设置所有的链路权重kα均为 1。使用 Python 开源第三方库Tensorflow 2.4.0 和Keras 对深度神经网络进行构建与训练，以下所有仿真均在同一块10 代i5-CPU 上进行，训练深度神经网络的超参数设置如表1 所示。

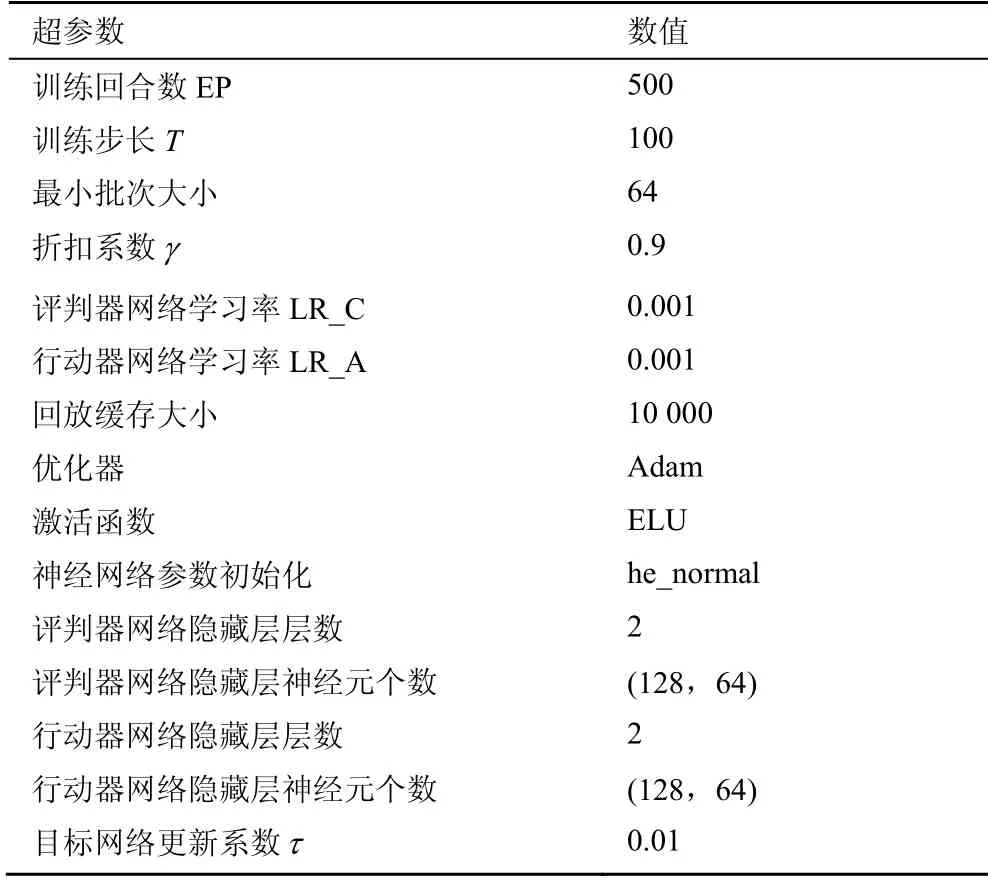
表1 深度神经网络超参数设置

3.2 算法收敛性分析

图3 展示了基于DDPG的智能无线发射功率控制算法的收敛情况。从图3 可以看到，算法在一开始需要收集一定数量的经验，此时进行随机探索，强化学习的回报值基本没有提升。当经验缓存达到训练要求数量，即算法开始训练后，回报值将随着回合数的增加逐渐升高，证明深度神经网络得到了有效的训练，并在较短的时间内就能够收敛。

图3 基于DDPG的智能无线发射功率控制算法收敛情况

由于超参数的选择对于深度学习的训练至关重要，图4 和图5 给出了深度神经网络中典型超参数学习率和隐藏层数对算法收敛情况的影响。从图4 可以看出，学习率过高或者过低的情况下，基于DDPG的智能无线发射功率控制算法均容易收敛至局部最优解，选取适当的学习率对训练效果有很大影响。

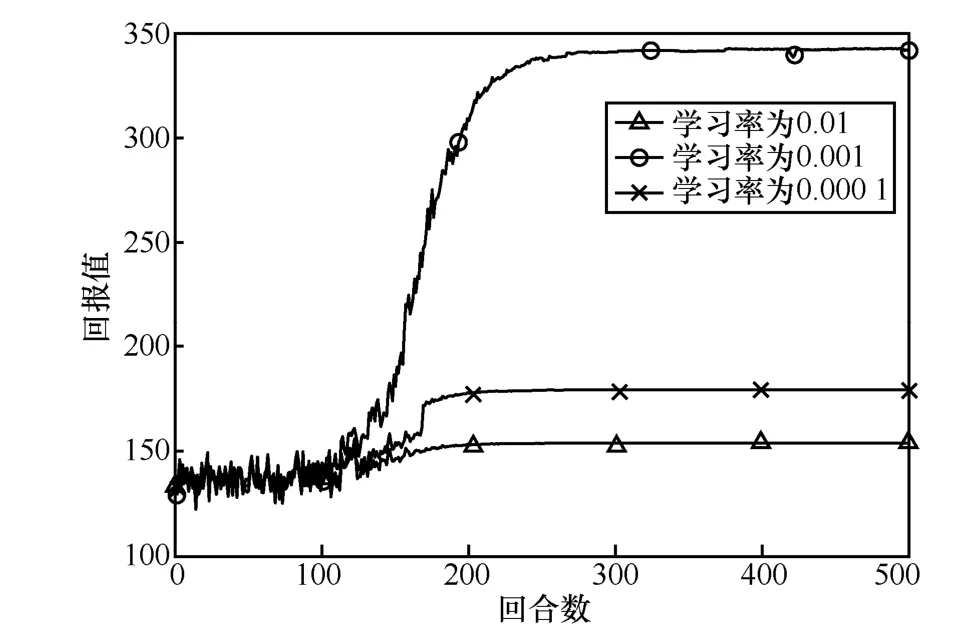
图4 学习率对算法收敛情况的影响

图5 隐藏层数对算法收敛情况的影响

从图5 可以看出，只使用一层隐藏层时神经网络不能很好地在强化学习中进行策略评估与策略改进，最终收敛至局部最优值，而使用两层及以上隐藏层时算法可以较好地收敛到全局最优值。但考虑到过多的隐藏层会增加计算与存储负担，且过多的隐藏层存在过拟合的风险，故本文最终选择使用两层隐藏层的深度神经网络。

3.3 算法性能分析

本节采用仿真手段，将本文所提智能无线发射功率控制算法训练得到的计算模型与传统优化算法WMMSE[6]和随机分配发射功率的方法进行比较。WMMSE 算法使用MMSE-SINR 等式[23]，即，将非凸的通信速率最大化问题式(4)转换为更高维度的可解的信号检测问题，MMSE 指用户的最小均方误差，如式(11)所示。

其中

运用块坐标下降法[24]求解式(11)得出原问题的最优解[6]。

算法效果方面，图6 给出了不同功率控制算法的平均传输速率的比较，本文算法在不同通信收发机数量的场景下均实现了超过随机分配算法的性能，且本文的智能功率控制算法能够实现平均传输速率逼近理论上最优的WMMSE 算法。

图6 不同功率控制算法的平均传输速率

算法效率方面，表2 和表3 给出在进行100 步功率控制情况下，不同算法在不同数量收发机场景中进行最优功率控制所需的运算时间。可以看出，WMMSE 算法所需运算时间随收发机数量的增长而快速增加，而本文算法只有小幅度改变。具体地，在5 对收发机的情况下，本文算法运算时间略少于WMMSE，但在10 对收发机的情况下，本文算法进行最优功率控制所需时间仅为WMMSE 算法的这是因为针对不同数量收发机的神经网络规模相同，故而本文所提算法的运算时间并不会发生显著变化。本文所提算法具备良好的可扩展性，能够有效适用于大规模用户的管理。

表2 5 对收发机的最优功率控制运算时间

表3 10 对收发机的最优功率控制运算时间

4 结束语

本文对多用户干扰情景下的智能无线发射功率控制算法进行了研究，提出了深度强化框架下的智能控制算法，以最大化通信系统的传输速率为目标优化发射功率控制策略。该算法借鉴深度强化学习中的深度确定性梯度下降技术，对行动器与评判器的2 个深度神经网络进行训练，进而获得对策略的精准评估与合理改进，采用经验回放和目标网络参数软更新的方法，确保算法具有良好的收敛性。仿真结果表明，该算法具有良好的收敛性，计算结果接近理论最优。